一种将递归过程转换为非递归过程的方法研究
2017-09-01张建波
张建波

摘 要:提出一种把递归过程转换为非递归过程的方法——递归树法,画出递归过程的递归树,然后通过对递归树的后根序遍历实现递归过程的非递归化,最后通过案例说明该方法的可行性和有效性。
关键词:递归;递归过程;非递归化;递归树
0 引 言
递归有思路清晰、代码简洁、易于理解等特点,是很多算法设计策略(如分治、回溯等)的核心内容,但是递归过程在计算机中实现时需要多次调用自身,增加了时空开销。很多学者对递归过程进行了深入研究[1-4],部分学者提出了一些递归过程的非递归化方法[4]。文献[3]和[5]虽然能很好地描述递归过程,但没有给出如何转换为非递归过程的一般方法;文献[4]提出了模仿法,该方法从简单实例入手,逐步过渡到较复杂的递归算法,初学者容易理解,但不能对复杂的递归过程进行直观分析。
由于递归树[2-3]作为研究递归过程的一种图形化方法,具有直观、简单等特点。笔者在此基础上提出一种基于递归树的递归过程的非递归化方法,该方法通过对递归树后根序遍历的思想实现递归过程的非递归化,具有直观、易于理解的特点。
1 递归与递归树
1.1 递归及递归过程的设计
一个问题的解法可以通过把该问题划分成若干子问题,若子问题比较简单,则直接求解;否则,采用与原问题相同的方法对这些子问题进行再划分、求解,依次类推,直到子问题变得较为简单,可以直接求解,当求出所有子问题的解后再对其进行汇总即可得到原问题的解,则称该问题为递归问题[5]。在计算机上,人们通常采用递归方法来求解递归问题,设计出的算法称为递归算法。
在递归方法中,递推动作和结束条件是两个重要组成部分。结束条件是指子问题比较简单、不必再划分成若干更小的子问题时应满足的条件,也就是说,当子问题满足结束条件时可以直接求解。当子问题不满足结束条件,还需要划分成更简单的子问题时需要执行的操作步骤称为递推动作。递推动作必须使递归算法能够逐步到达结束条件。递归算法的一般模型为:
algorithm
if (
return (direct value); /* 直接求解,并返回结果 */
else /* 递归 */
return (
}
递归的整个过程可分为两个子过程:递推过程和回归过程。当不满足结束条件时,递归过程需要不断执行递推动作的过程为递推过程;当满足结束条件时停止递推动作并沿递推过程的逆过程进行回溯的过程为回归过程。递推过程是对子问题不断细化使其逐步向结束条件靠近的过程;回归过程是返回各子问题的结果并汇总直到得出问题最终解的过程。在一些复杂的递归算法中,递推过程和回归过程是交替出现的。
1.2 递归树及其构建
在计算机中,递归调用由若干个子递归调用组成,而子递归又有更下一层的子递归调用,这种逐层调用的轨迹可以用递归树来刻画。
递归树是一种有序树,树根为递归算法的入口,根的值为递归参数值,如果递归参数值满足结束条件,则开始回归过程,此时根结点也是叶子结点;否则,递归算法需要调用自身若干次,每调用一次就相当于樹根多了一个分支,即产成一棵子树;每棵子树也是递归树。
递归树是研究递归问题与递归算法之间的一座桥梁。在分析具体问题时,我们首先从根结点出发,按照递归的递推过程不断建立并扩展递归树,当满足结束条件时,该递归树的根结点就成了叶子结点,然后根据建树的逆序过程,不断向根部返回并得到最终解。
与一般的非递归算法的分析方法——“单步跟踪法”不同,递归树可以直观、清晰地描述递归算法的整个过程。对于一般的非递归算法,设计者常用单步跟踪法动态演示算法的执行过程;但在递归算法中,由于不同层次递归时的参数是不一样的,对于层数较多、递推过程和回归过程交替出现的递归算法,“单步跟踪”法容易导致设计者对当前调用环境中的参数产生混乱,因此,递归树法可以有效避免“单步跟踪”法的缺点。
2 案例分析
正确设计一个递归算法的前提是分析问题、明确具体任务并给出清晰的递归定义。接下来,笔者通过两个案例来说明递归树在研究递归算法并把递归算法转换为相应的非递归算法中的作用。以下算法均采用类C++程序设计语言进行定义和描述。
2.1 汉诺塔(Tower of Hanoi)问题
用状态变量(n, A, B, C)表示“把 n 个盘子从A柱,借助于B柱移动到C柱上”。参数n表示当前的盘子数量;参数A、B和C分别为柱子的编号。汉诺塔问题的递归解法为:
void Hanoi_R(n, A, B, C) {
if (n == 1)
move (A, C); /* 相当于 Hanoi(1, A, B, C) */
else {
Hanoi_R (n-1, A, C, B);
move (A, C);
Hanoi_R (n-1, B, A, C);
}
}
用递归树描述该递归算法(以n = 3为例),如图1所示。
图1直观地描述了n(= 3)个盘子时的解决方法,其中,递推动作包括3个步骤,即每个度为3的结点下的3个结点;递归的结束条件对应n = 1的结点。
从图1中可知汉诺塔问题的递归树为3叉树。其中n为1时表明结点为叶子,可直接求解,不必再递归。如果对该3叉树进行后根序遍历(此问题只须遍历叶子结点)可得到整个问题的解。
为了能区别同一结点下的所有子女(Child)的处理次序,把结点结構改为(n, A, B, C, k),其中k表示该结点是其双亲结点的第几个子女。这样,汉诺塔问题要解决的问题是(3, A, B, C, 1)对应的解,相应的非递归算法如下:
void Hanoi_I(n, A, B, C) {
StackInitialize S; /* 初始化栈 */
StackElement p =: (n, A, B, C, 1); S.Push(p); /* 树根p入栈 */
while(!S.IsEmpty( )) {
S.getTop(p); /* 取栈顶 */
if(p.n == 1) { /* 1) 若栈顶元素的 n 值为 1,*/
S.Pop(p); move(p.A, p.C); /* 出栈并输出相应的解 */
if(p.k == 1) { /* 1.1) 若栈顶元素的 k 值为 1,则 */
p =: (1, p.A, p.C, p.B, 2); S.Push(p);/* 其右兄弟(第2步)入栈 */
}
else if(p.k == 2){ /* 1.2) 若栈顶元素的 k 值为2,则 */
S.getTop(p);
p =: (p.n-1, p.B, p.A, p.C, 3); S.Push(p); /* 其右兄弟(第3步)入栈 */
}
else { /* 1.3) 若栈顶元素的 k 值为3,则 */
/* 1.3.1) 若栈不空且栈顶元素的 k 值为3,向上回溯 */
while(p.k == 3 && !S.IsEmpty( )) S.Pop(p);
/* 1.3.2) 若栈不空,则k只能为1,此时其右兄弟(第2步)入栈 */
if(!S.IsEmpty( )) {
p =: (1, p.A, p.C, p.B, 2); S.Push(p);
}
}
}
else { /* 2) 若栈顶元素的 n 值不为 1,则 */
// 该子问题还需要再划分,把划分的第1步所对应的结点入栈
p =: (p.n-1; p.A, p.C, p.B, 1); S.Push(p);
}
} /* while */
}
2.2 Ackerman函数的计算
Ackerman函数的定义为
可以用状态变量(m,n)表示函数akm(m, n)的值。由于这是一个递归定义,因此很容易用递归方法设计出其递归解法。
根据Ackerman函数的定义,其递归程序如下:
int akm_R(int m, int n) {
if(m == 0) return n+1;
else if(n == 0)return akm_R(m-1, 1);
else return akm_R(m-1, akm_R(m, n-1));
}
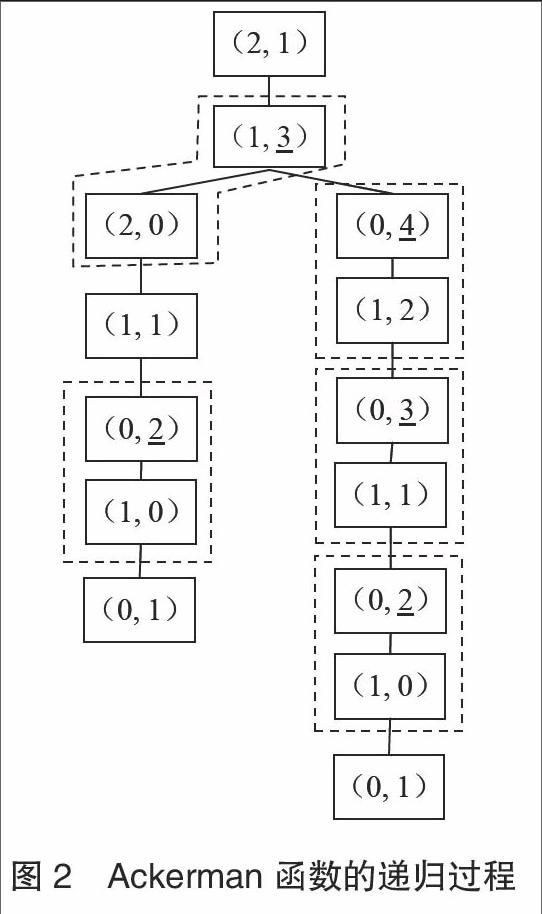
其对应的递归树如图2所示(以m = 2,n = 1为例),其中虚线框内的结点表示第三种情况(m ≠ 0,n ≠ 0),需要两次递归。
该树的非递归算法如下:
int akm_R(int m, int n) {
StackInitialize S; /* 初始化栈 */
StackElement p =: (m, n);
S.Push(p); /* 树根入栈 */
while(!S.IsEmpty( )) {
S.getTop(p); /* 取栈顶 */
if(p.m > 0 && p.n > 0) { /* 1) 第三种情况,需要两次入栈 */
S.Push(p.m-1, -1); /* 1.1) 第1次进栈,用 n == -1 表示其值待求 */
S.Push(p.m, p.n-1); /* 1.2) 第2次进栈 */
}
else if(p.m > 0 && p.n == 0) /* 2) 第二种情况,入栈一次 */
S.Push(p.m-1, 1);
else if(p.m == 0) { /* 3) 第一种情况,直接求解并回归 */
/* 3.1) 出栈,用p表示出栈元素 */
if(!S.IsEmpty( ))S.Pop(p);
/* 3.2) 若p中没有待求项(第一种情况),则直接算出结果并向根部返回 */
if(p.n != -1) n = p.n+1;
while(p.n != -1 && !S.IsEmpty( )) S.Pop(p);
/* 3.3) 若p中有待求项,则把结果赋给待求项,入栈,开始新递归 */
if(!S.IsEmpty( )) { m = p.m; p.n = n; S.Push(p); }
}
} /* while */
return n;
}
Ackerman函数是一个增长速度很快的函数。在硬件为4G内存、I3-2120 3.30GHz CPU,软件为Windows 7(64位)操作系统、DEV C++ 5.9.2环境下,以m = 4,n = 1为例,非递归算法在约90秒左右的时间里算出结果为65 533,栈里存储的最大元素个数为1 063 453 415,而递归算法因空间资源消耗过大无法算出结果。
3 结 语
在实际中,递归问题是一个比较常见的问题,如n皇后问题、迷宫问题、二叉树遍历等,而递归方法是解决递归问题的一个基本方法。利用开发工具(如Visual C++、DEC C++)的调试功能观察递归算法的运行过程往往有较高的难度,特别是对于递归层数较高的算法。另外,递归算法需要依靠系统提供的递归栈来实现多次自身调用,这既耗费时间又耗费空间,因此人们常用迭代或栈来设计相应的非递归算法以提高效率,但是对于初学者来说,设计非递归算法的难度往往较大。
参考文献:
[1] 张俊. 基于递归树的递归调用分析[J]. 实验室研究与探索, 2010, 29(3): 83-87.
[2] 黎远松. 基于树的递归算法分析技术[J]. 四川理工学院学报(自然科学版), 2012,25(4): 50-51.
[3] 周集良. 描述递归算法的有效工具: 递归树[J]. 怀化师专学报,1999, 18(5): 41-44.
[4] 张玉华. 模仿法在数据结构递归算法设计中的教学实践[J]. 计算机教育, 2016(1): 134-138.
[5] 殷人昆. 数据结构(用面向对象方法与C++语言描述)[M]. 2版. 北京: 清华大学出版社, 2007: 101-102.
(编辑:郭田珍)
