超声冲击改善奥氏体不锈钢表面状态的数值分析
2017-09-01谭伟杨新俊周新夏强
谭伟 杨新俊 周新 夏强
(江苏省特种设备安全监察检验研究院常熟分院)
应用研究
超声冲击改善奥氏体不锈钢表面状态的数值分析
谭伟*杨新俊 周新 夏强
(江苏省特种设备安全监察检验研究院常熟分院)
基于Johnson-Cook方程建立超声冲击处理的三维有限元模型,研究超声冲击处理奥氏体不锈钢S30408的动力学过程,分析覆盖率、搭接率、冲击次数对表层残余应力分布、塑性变形及形貌的影响。结果表明,覆盖率的增加提高了冲击处理后材料表面的压应力值,同时降低了冲击坑边缘的最大拉应力值。进一步增加覆盖率无法消除表面的残余压应力高值区域,但是通过提高冲击处理的搭接率可以有效地降低材料的表面拉应力,从而显著提高处理后S30408材料的表面质量。
超声冲击 有限元 残余应力 不锈钢 覆盖率 搭接率
0 前言
焊接接头是金属设备构件中的薄弱环节,焊接接头的应力腐蚀开裂 (SCC)是焊接接头失效的主要形式之一。以不锈钢焊接接头为例,在石油化学工业中,其应力腐蚀开裂事故约占湿态腐蚀损坏事故的40%~60%[1]。每年由于焊接接头应力腐蚀开裂所带来的经济和社会损失十分巨大。
作为一种表面强化处理工艺,超声冲击处理因其快速、高效、绿色无污染等特点,在对时间、费用、环境和强化效果要求比较高的情况下 (如大型化工压力容器设备的高处作业、制造及维修等),显示出明显的优势[2]。焊接接头表面经超声冲击强化处理后产生极为强烈的塑性变形,使表层焊接残余应力从原先的拉应力状态转变为压应力状态,可有效阻止应力腐蚀开裂的发生,从而大大提高焊接构件的抗应力腐蚀能力[3]。
因此,了解和分析超声冲击处理残余应力场分布与工艺参数之间的关系,对于超声冲击处理的应用非常重要。但是,目前测试残余应力的方法和手段,例如无损检测方法,在实验中用于残余应力的实际测量,不仅需要耗费大量的时间、人力以及费用,而且还难以完全掌握处理后工件的三维残余应力场。数值模拟因其高效性和经济性已在实验研究以及工业设计中得到越来越多的应用,通过有限元方法对超声冲击处理进行动态模拟,可节省实验的巨大投入,并且得到处理后三维残余应力场的完整信息,目前数值模拟已经成为研究超声冲击处理的重要手段[4]。本文拟采用有限元方法,研究覆盖率、搭接率、冲击次数等对超声冲击处理后材料表层残余应力分布、塑性变形等的影响。
1 超声冲击处理原理
超声冲击处理设备由一个频率为21 kHz、输出功率为0.5 kW(可变)的超声发生器和换能器、变幅杆以及若干安装在变幅杆头部的冲击针头组成。冲击针头排成一定的阵列,可在被处理工件表面与变幅杆头部自由移动。其工作原理如图1所示。
对于超声冲击处理工艺,有两个重要的参数会对处理后残余应力场产生影响:(1)冲击处理强度;(2)覆盖率。冲击处理强度主要与冲击针单次冲击输入的能量有关,而覆盖率则与材料被处理的面积有关。
根据文献 [5-6],超声冲击处理强度可用每次冲击输出的能量P来表示。P(单位:W·g-1)是一个重要参数,可通过式 (1)计算:
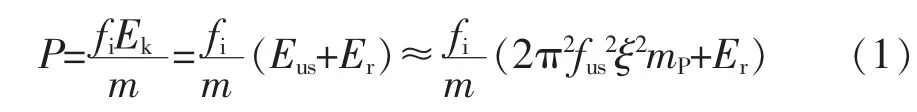
式中Eus——变幅杆传递给冲击针头的动能;
fus——振动频率;
ξ——振幅;
Er——移动整个冲击头所传递的能量(与Eus相比,一般忽略不计);
fi——冲击频率,一般取值为3±0.5 kHz;
m——质量系数,表示针头质量mP和工件质量ms之间的关系。而超声冲击针头的运动速度 v可通过式 (2)求得:

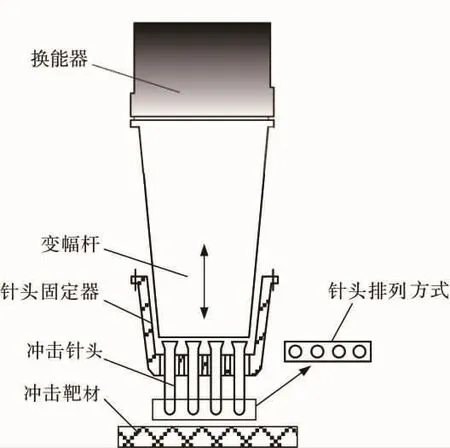
图1 超声冲击处理工作原理
式(2)中符号定义与式(1)相同。由式 (1)和式 (2)可见,单次冲击针头输出能量P主要与针头质量、振幅、冲击频率有关,其中冲击频率与冲击振幅又确定了冲击速度。所以,不同的冲击速度确定了超声冲击处理的强度。本实验采用的超声冲击设备参数如表1所示。通过计算可得到超声冲击的相关计算参数。超声冲击处理覆盖率的定义与普通喷丸相同,采用处理后变形区域的面积与处理区域的总面积的比值来表示 (如图2所示)。本文采用文献 [7]中的计算方法来确定数值模拟中的覆盖率。冲击处理后等效塑性应变 (PEEQ)大于0的区域为变形区域。模型中覆盖率通过式(3)确定:

式中r——处理后冲击目标表面塑性区域半径;
S——冲击目标的面积;
C——覆盖率。

表1 超声冲击设备参数
本研究中,当覆盖率小于100%时,覆盖率的变化是通过改变冲击目标的几何尺寸来达到的。超过100%的覆盖率则是指冲击处理的时间与100%处理时间的比值,通过多次冲击100%覆盖率时的冲击目标来实现。

图2 覆盖率定义示意图
2 超声冲击有限元模型
2.1 材料本构模型的选取
对于大部分的钢材而言,其弹性模量以及密度分别为:E=210 GPa,ρ=7 800 kg/m3。应力波在钢材中的传播速度可通过式 (4)计算:
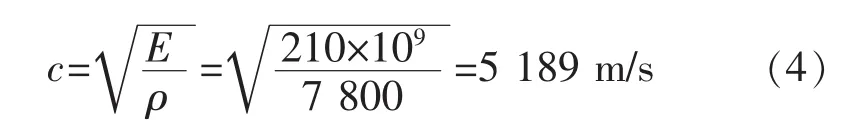
超声冲击处理过程中,针头冲击速度很高,被处理材料的厚度一般超过2 mm,在该区域内,应力波的作用时间约为4×10-7s。冲击过程中,撞针与工件表面的接触时间一般在10-5s数量级,应力波的作用时间与接触时间相比无法忽略,所以超声冲击过程的数值计算中,应变率的作用不能忽略。考虑到这个原因,本文采用Johnson-Cook模型作为被处理材料的本构模型,该模型适用于大多数发生高应变速率变形的材料。该模型中材料的流动应力可表示为式 (5):
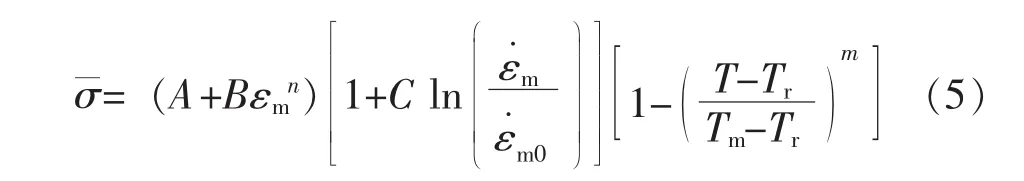
应力;
A——环境温度(Tr)下的初始屈服应力;
B——应变硬化参数;
C——应变率敏感系数;
εm——等效塑性应变;
ε˙m——等效塑性应变率;
ε˙m0——参考应变率;
T——当前温度;
Tm——材料的熔化温度;
n——应变硬化指数;
m——热软化系数。
本文中所采用的材料为S30408,通过标准拉伸试验获得其应力应变曲线,如图3所示。
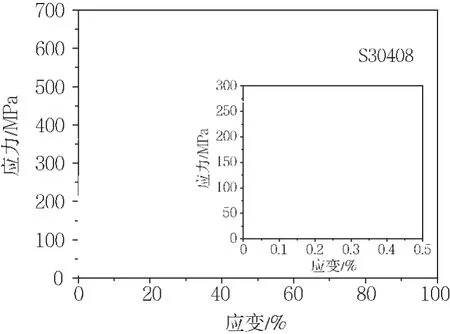
图3 S30408应力应变曲线
Johnson-Cook模型中,A、B和n通过拉伸应力应变曲线可以获得,而C、m等值与材料的动态响应有关,需通过Hopkinson压杆实验来确定,由于缺乏相关实验设备,相关参数通过文献获取。文献中关于S30408的动态参数,除C外取值变化不大。不同文献中关于C值的选择有两个取值范围[8]:(1) 0.06~0.07;(2) 0.02~0.025。 研究发现, 对于国内304不锈钢,采用0.06~0.07取值获得的残余应力值与实验相比偏高,而采用0.02~0.025之间的取值更为合适 (低的C值意味着较低动态屈服强度)。本文中采用的S30408具体参数见表2。

表2 材料S30408的力学性能
2.2 材料阻尼的选取
有限元的显示动力分析过程中,冲击过程的计算会造成冲击后长时间的残余应力振荡。这种响应振荡如果不能有效地抑制,就会导致误差的累积,对计算结果的收敛造成不利的影响。特别是在重复冲击的情况下,前一次冲击形成的残余应力振荡会对后续冲击的结果产生较大影响,在一定深度方向造成拉应力[9]。为了避免这个影响,需在冲击材料中引入合适的阻尼:

式中ξ——模态阻尼;
ω——材料固有频率;
α——质量比例阻尼;
β——刚度比例阻尼。
α用于低频响应的衰减,β用于高频响应的衰减。
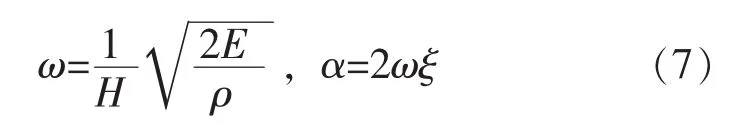
式中E——材料的弹性模量;
ρ——材料密度;
H——计算单元的高度。
对于快速衰减的低频振荡,ξ取值0.5,刚度比例阻尼 β取值 2×10-9[10]。
2.3 模型的尺寸、网格以及边界条件
考虑到超声冲击过程中周期性的特点,基于Meguid的阵列冲击模型[11],采用软件ABAQUS建立一个周期性单元的三维有限元模型 (如图4所示)。超声冲击处理的有限元模型由目标靶材以及4根超声冲击针组成,靶材为一长方体,冲击材料为立方体,四根冲击针位于立方体的四个角上。

图4 超声冲击处理有限元模型
立方体冲击目标的尺寸为3 mm(D)×3 mm(D)×6 mm (H),冲击表面网格细化,细化区域深度(H1)为3 mm,冲击针半径(R)为1.5 mm,网格划分选用C3D8R。通过网格敏感性检查,确定冲击材料的网格为六面体网格,网格尺寸为0.4 mm。网格细化区域,为网格尺寸0.05 mm的六面体网格。冲击针头为0.01 mm的四面体与六面体混合网格。
边界条件做如下设置:冲击材料的四面设为对称边界条件,底部设为固定边界条件。冲击过程的接触参数做如下设定:以惩罚算法定义冲击处理的接触过程,并取摩擦系数为0.2。为了减小沙漏问题对于计算精度的影响,通过引入人工刚度来限制沙漏模式的扩展,沙漏参数取3[12]。
3 结果与讨论
3.1 覆盖率的影响
图5是在5 m/s冲击速度下,不同覆盖率冲击处理后的PEEQ云图,显示出了不同覆盖率下冲击区域尺寸的变化。图中C表示覆盖率,D为冲击区域的边长。
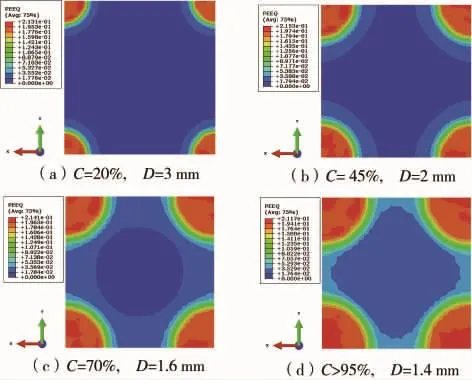
图5 不同覆盖率下冲击处理后的PEEQ云图
图6显示了不同覆盖率下处理后材料表面残余应力分布。冲击处理后,拉应力高值区域依然位于冲击后凹坑的边缘且大小不变。随着冲击覆盖率的增加,高应力区域逐渐融合。覆盖率的提高虽然不能消除拉应力高值区域,但是表面的最大拉应力值却随着覆盖率的增加而降低,从而提高了处理后S30408的表面质量,改善了处理后材料的抗应力腐蚀的性能。
从图7可以看出,覆盖率低于100%时,超声冲击处理后残余应力的深度以及最大残余应力的位置随覆盖率的变化很小。最大残余压应力从512.9 MPa降低到499.0 MPa。而残余应力的深度也仅仅从1.23 mm降低到1.04 mm。最大残余压应力值,以及残余应力深度的降低是由于超声冲击处理过程中,覆盖率的增加降低了冲击处理产生的强化效果。因为在冲击区域边缘会同时产生表面波 (如Rayleigh波和切变应力波等),这些表面波向冲击区域的中心汇聚,从而引起这一局部区域的反向塑性应变,降低了此处的表层残余压应力水平。但是由于冲击过程中,残余应力的强化效果主要通过纵向应力波来实现,所以最大压应力值以及压应力深度降低得并不明显[14]。但是表面残余压应力值则随着覆盖率的增加明显提高。在这个过程中,表面残余压应力从155.5 MPa增加到275.9 MPa。
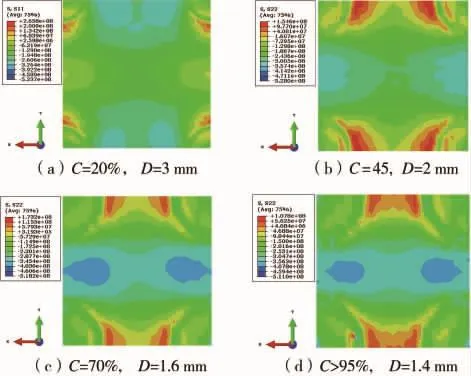
图6 不同覆盖率下表面残余应力分布 (单位:Pa)

图7 不同覆盖率处理残余应力随深度方向的变化
图8给出了不同覆盖率下,冲击处理后表面凹坑的尺寸。覆盖率的增加会减小凹坑的深度与宽度,从而降低处理后材料表面的粗糙度,降低由此产生的应力集中。沿深度方向的等效塑性应变则基本不随覆盖率的增加而变化。如图9所示,塑性应变大小以及深度几乎保持不变。
3.2 搭接的影响
上述研究中只讨论了覆盖率低于100%时的情况。结果表明,无论冲击参数如何改变,处理后的表面月牙状残余拉应力高值区域始终存在,这会对处理后的材料表面产生负面的影响。在实际超声冲击处理的情况中,当覆盖率大于100%时,多次冲击无法做到准确冲击同一位置,冲击位置的偏移会造成冲击后塑性区域不能完全重叠,如图10所示。这种冲击区域的重叠能够有效降低表面的粗糙度,同时降低表面残余拉应力的值。可以通过搭接率η来定义这种冲击区域重叠的大小,如式(8)所示:


图8 不同覆盖率处理后表面凹坑尺寸
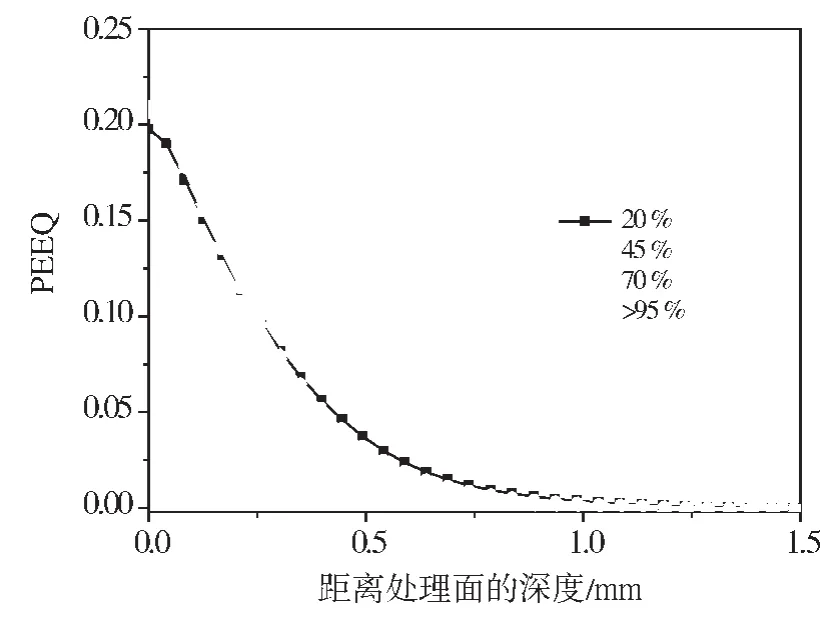
图9 不同覆盖率下等效塑性应变沿深度方向的变化
式中ΔL——相邻凹坑之间的搭接长度;
D——冲击后塑性变形区域的直径。
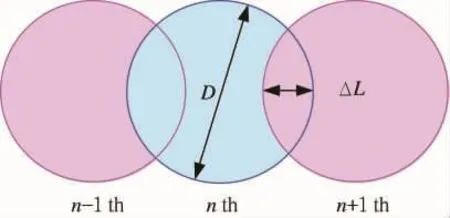
图10 搭接率示意图
100%的覆盖率则表示间隔的两个塑性区域相切于同一点。通过该参数,可以研究冲击点的偏移对拉应力高值区域的影响,分析在高于100%覆盖率时,不同搭接率对冲击后残余应力场特别是表面应力分布的作用。
研究结果表明,随着搭接率的增加,表面残余拉应力高值区域逐渐消失。当搭接率达到0.7后,中间凹坑四周的应力梯度减小,表面应力分布趋缓(见图11)。搭接率还能明显改变沿厚度方向残余应力的分布,增加搭接率能够提高覆盖率,从而有效地提高残余压应力的厚度。但是搭接率的增加对于表面残余应力值几乎没有影响,如图12所示。
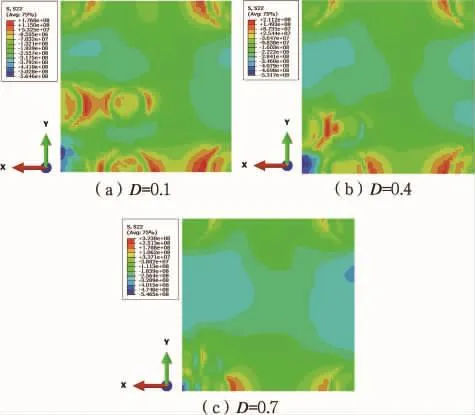
图11 搭接率对表面残余应力的影响 (单位:Pa)
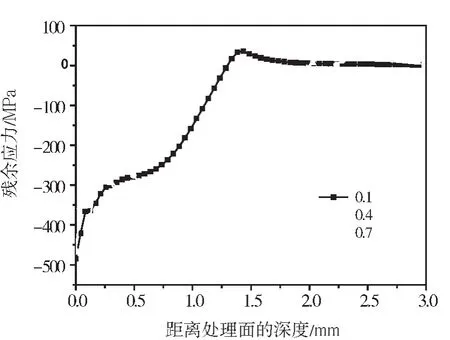
图12 不同搭接率下残余应力沿深度的分布
3.3 重复冲击的影响 (高覆盖率下)
作为一种通过塑性变形进行表面处理的工艺,超声冲击处理可用于实现金属材料表面纳米化。但是实现这一过程需要在材料表面产生剧烈的塑性变形,这就意味着需要在处理的过程中大幅增加冲击的覆盖率。研究表明,对于S30408不锈钢材料来说,必须达到1000%以上的覆盖率才能在材料表面产生可以检测的纳米晶粒层,这就需要在处理过程中针头对材料表面产生多次重复冲击。为了研究高覆盖率下的冲击过程,对模型进行简化,假设同一针头多次冲击同一位置,从而获得高覆盖率下超声冲击处理对S30408的影响。
图13为3 m/s冲击速度下多次冲击处理后的残余应力场。重复的冲击能够有效减小处理后材料表面的残余拉应力,降低表面的残余应力梯度,表面月牙状的高值应力区域也随着冲击次数的增加逐渐消失。图14为3 m/s与5 m/s冲击速度下残余应力沿深度方向的分布。无论冲击速度多大,当冲击次数达到6次以后,沿深度方向的残余应力均趋于饱和;进一步增加冲击次数,应力值以及残余压应力深度增幅趋缓。在3 m/s冲击速度下,处理后材料表层塑性变形的厚度从初始的0.96 mm开始增加,6次冲击后达到饱和,约为1.47 mm。而在5 m/s冲击速度下,处理后材料表层塑性变形的厚度从初始的1.55 mm开始增加,在6次冲击后达到饱和,约为1.80 mm。由此可见,沿深度方向无论残余应力还是塑性变形在6次冲击后均达到饱和。但是表面塑性变形量仍随冲击速度不断增加,并可以使表面塑性持续累积,从而细化晶粒。由于塑性变形的深度无法一直增加,从而限制了超声冲击处理后纳米层以及塑性变形层的厚度变化,如图15所示。
4 实验验证
4.1 残余应力测量
以5 m/s冲击速度、100%覆盖率超声冲击处理S30408不锈钢材料。采用X-350A型X射线应力应变测定仪测定处理后试样的残余应力。测定前先用零应力铜粉对分析仪进行标定,测量时对试样沿厚度方向逐层剥离,从而获得残余应力随着深度变化的曲线,如图16所示。
4.2粗糙度测量
表面凹坑的尺寸通过测量表面粗糙度来表征。依据 《表面粗糙度比较样块》技术标准,采用峰高与低谷之间的算术平均值Ra的大小来衡量表面粗糙度,其计算式为:
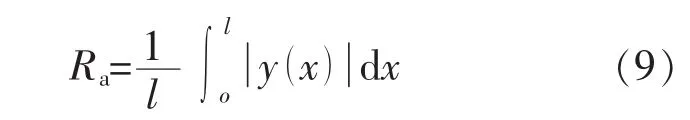
式中l——取样长度,用于判别具有表面粗糙特
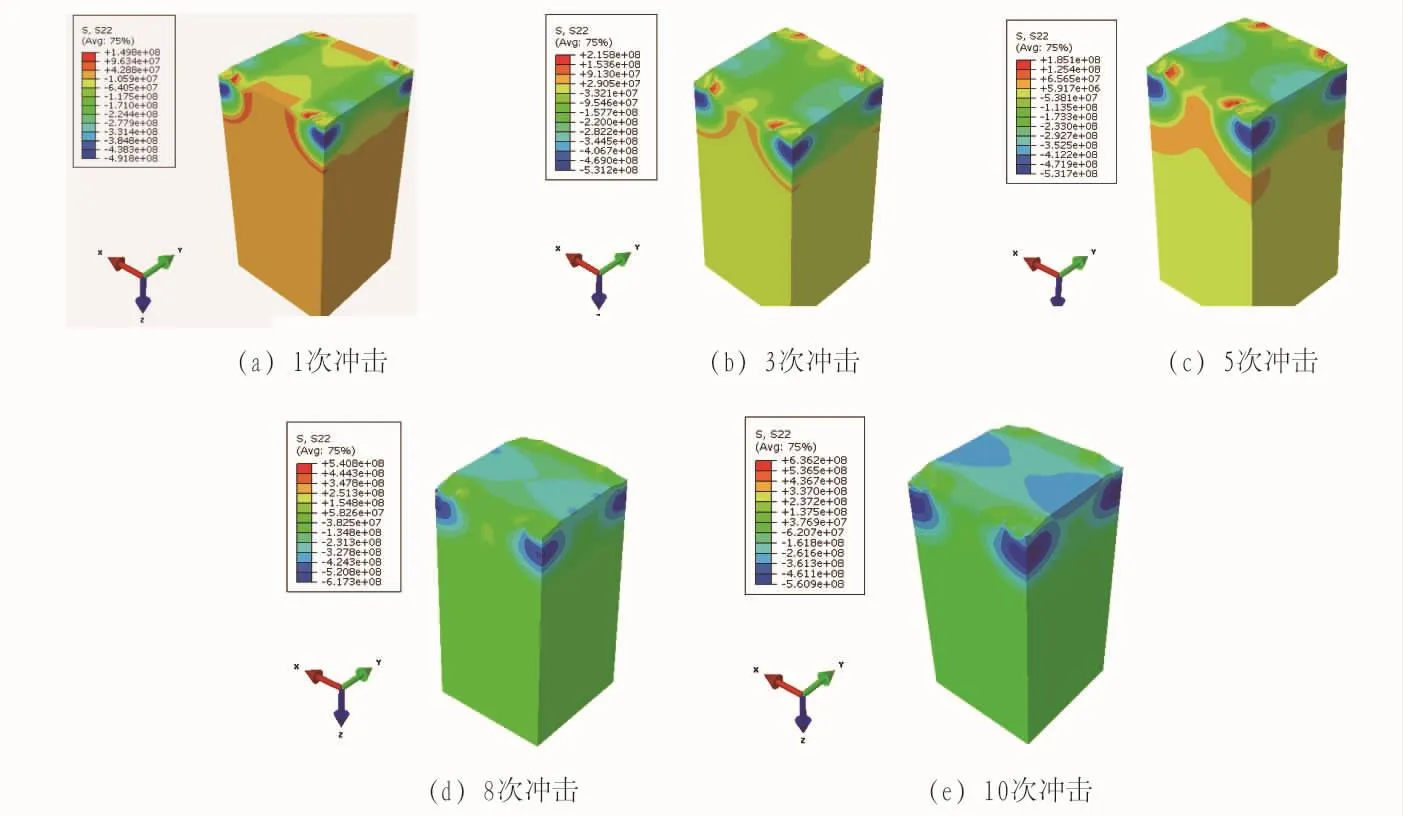
图13 多次冲击的应力云图
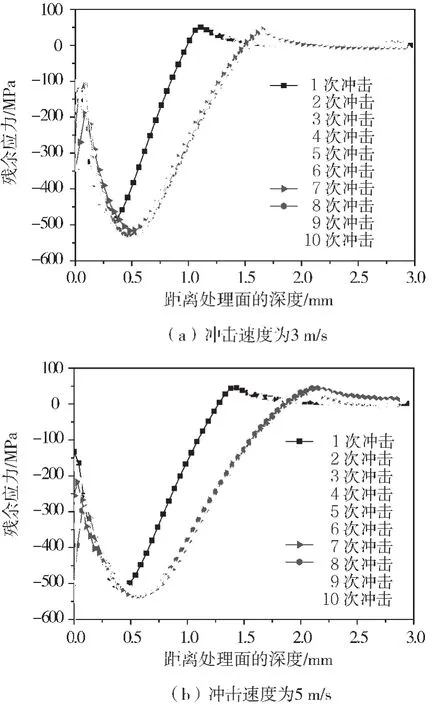
图14 不同速度下多次冲击后沿深度方向残余应力分布
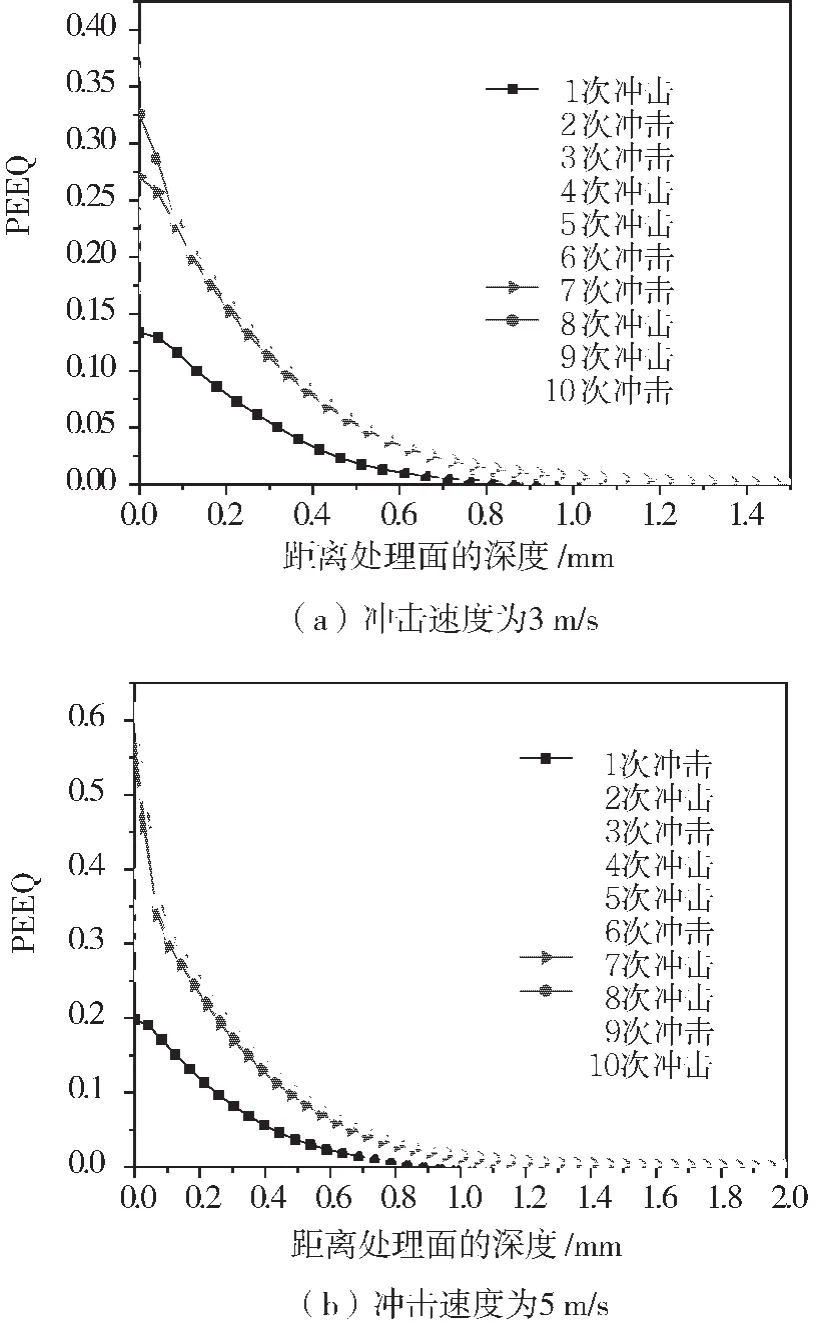
图15 不同速度下多次冲击后沿深度方向塑性应变
征的一段基准长度;
y——轮廓偏距,即轮廓上的点至基准线-
表面轮廓平均的距离。
实验采用TR100袖珍式表面粗糙度仪对试样处理前后的表面粗糙度进行测量,采用轮廓算术平均偏差Ra作为表面粗糙度的评定参数,取样长度为0.8 cm,实验结果如图17所示。
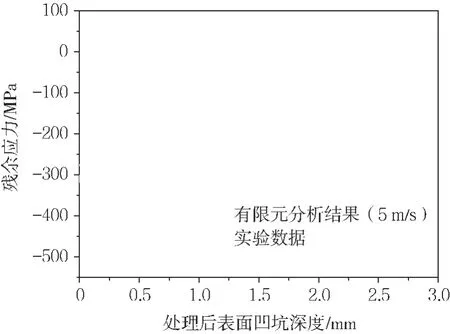
图16 残余应力测量值
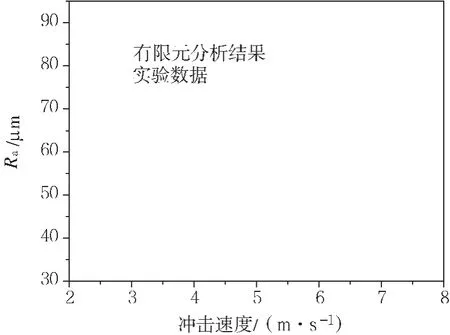
图17 粗糙度测量值
实验结果表明,通过有限元的方法获得的表层残余应力场以及表面形貌与实验结果吻合较好。但是,由于覆盖率无法非常精确地控制,从而产生误差,导致粗糙度实验值均小于数值计算的结果。
5 结论
本文基于Johnson-Cook模型,通过数值模拟方法研究超声冲击过程中奥氏体不锈钢S30408材料的动态响应过程,获得覆盖率、搭接率、冲击次数等处理参数对表层残余应力场、塑性变形及形貌的影响,具体结论如下:
(1)该模型能够有效地预测超声冲击处理后材料表面的微观形貌及应力分布情况。
(2)覆盖率的增加提高了冲击处理后材料表面的压应力值,同时降低了冲击坑边缘的最大拉应力值,提高了处理后S30408材料的表面质量。
(3)覆盖率的增加没法消除表面的残余压应力高值区域 (呈月牙状,位于冲击坑的边缘),但是通过提高冲击处理的搭接率可以有效地降低材料的表面拉应力。
(4)多次冲击的情况下,尤其当冲击次数达到6次后,材料的表面残余应力以及塑性层厚度达到饱和,但是表面塑性变形量随冲击次数不断增加,使表面塑性变形持续累积,从而细化晶粒。
[1]陆世英.不锈钢应力腐蚀事故分析与耐应力腐蚀不锈钢 [M].北京:原子能出版社,1985.
[2]STATNIKOV E S.Applications of operational ultrasonic impact treatment (UIT) technologies in production of welded joints.International Institute of Welding,1997,XII-1667-97:1-19.
[3]KIRK D,RENDER P E.Effects of peening on stress corrosion cracking in carbon steel, ICSP7: 167-176.
[4]张洪伟,张以都,吴琼.喷丸强化过程及冲击效应的数值模拟 [J].金属学报, 2010, 46(1):111-117.
[5]MORGYUK B N,PROKOPENKO G I.Fatigue life improvement of α-titanium be novel ultrasonically assisted technique [J].Materials Science Engineering:A, 2006,437(2): 396-405.
[6]MORDYUK B N,PROKOPENKO G I.Ultrasonic impact peening for the surface properties’management[J].Journal of Sound and Vibration, 2007, 308(3-5): 855-866.
[7]HASSANI-GANGARAJ S M,GUAGLIANO M,FARRAHI G H.Finite element simulation of shot peening coverage with the special attention on surface nanocrystallization[J].Procedia Engineering, 2011(10): 2464-2471.
[8]LEE S, BARTHELAT F, HUTCHINSON J W.Dynamic failure of metallic pyramidaltrusscore materialsexperiments and modeling [J].International Journal of Plasticity, 2006, 22(11): 2118-2145.
[9]张洪伟,张以都,吴琼.喷丸强化残余应力场三维数值分析 [J].航空动力学报,2010,25(3):603-609.
[10]张洪伟,陈家庆,张以都.基于多丸粒模型的喷丸表面强化过程数值模拟 [J].塑性工程学报,2012,19(5):18-125.
[11]MEGUID S A,SHAGAL G,STRANART J C.3D FE analysis of peening of strain-rate sensitive materials using multiple impingement model[J].International Journal of Impact Engineering, 2002, 27(2): 119-134.
[12]凌祥,彭薇薇,倪红芳.喷丸三维残余应力场的有限元模拟[J].机械工程学报,2006,42(8):182-189.
Numerical Analysis of Ultrasonic Impact Treatment to Improve the Surface State of Austenitic Stainless Steel S30408
Tan WeiYang Xinjun Zhou Xin Xia Qiang
Based on the Johnson-Cook equation,a three-dimensional finite element model of ultrasonic impact treatment was established to study the dynamic process of austenitic stainless steel S30408 treated by ultrasonic impact.The influences of coverage rate,overlap rate and impact times on the residual stress distribution,plastic deformation and morphology of the surface layer were analyzed.The results showed that the increase of the coverage raised the compressive stress on the surface of the material after shock treatment,and reduced the maximum tensile stress at the edge of the impact pit.The high value region of tensile residual stress couldn't be eliminated by continuous increase the coverage.However,the surface tension stress of the material could be effectively reduced by increasing the lapping rate of the impact treatment,and the surface quality of the S30408 after treatment was remarkably improved.
Ultrasonic impact;Finite element;Residual stress;Stainless steel;Coverage rate;Overlap rate
TQ 050.4
10.16759/j.cnki.issn.1007-7251.2017.08.005
2016-11-01)
*谭伟,男,1969年生,工程师。常熟市,215500。
