无双线性对的无证书聚合签密方案
2017-09-01王梦殊祁正华
王梦殊,祁正华
(南京邮电大学 计算机学院,江苏 南京 210003)
无双线性对的无证书聚合签密方案
王梦殊,祁正华
(南京邮电大学 计算机学院,江苏 南京 210003)
无证书聚合签密是把多个用户对不同消息产生的不同签密聚合成一个签密,不仅保证信息传输的机密性和认证性,而且降低了信息传输的功耗,因此应用于大规模分布式通信中的多对一模式。聚合签密方案大多需要进行双线性对运算,效率不高。为此,提出了一种高效的无线性对的无证书聚合签密方案。该方案在随机预言模型下应用离散对数,对原有的无双线性对聚合签名算法进行了改进,形成了更为安全、高效的聚合签密方案。基于所提出的聚合签密方案安全模型,分析研究了随机预言模型下提出方案的不可伪造性和机密性,并对其有效性和可行性进行了验证。理论分析表明,所提出的方案在多个签密者存在的条件下,不仅具有机密性、不可伪造性,还具有更高的计算效率。
无证书聚合签密;随机预言模型;无双线性对;离散对数问题
0 引 言
签密[1]在合理逻辑步骤里同时完成信息的签名与伽马。2009年,Selvi等[2]提出了基于身份的签密方案,并证明了其安全性。祁正华[3]进行了基于身份的签密方案研究;于刚[4]进行了若干签密研究。聚合签密能将多个密文进行聚合且提供批量验证,极大降低了信息传输的功耗,大幅提升了签密验证的效率,适用在大规模分布式通信的多对一模式下。Ren等[5]提出了一种可证明安全的聚合签密方案;苏爱东等[6]提出了一种密文长度固定的聚合签密方案,但未给出形式化的安全性证明。
无证书密码体制于2003年由Al-Riyami等[7]提出,解决了公钥证书管理及验证问题和密钥托管问题。Barbosa等[8]提出了无证书签密方案并给出了安全模型。陆海军[9]和Eslami等[10]在随机预言模型下分别提出了可证明安全的无证书聚合签密方案;Qi等[11]提出了无证书环签密方案,但是上述签密方案中用了较多双线性对运算,因此效率较低。Qi等[12]对基于身份的聚合签密进行了安全性分析,但使用了双线性对。周彦伟等[13]提出的无证书聚合签名方案运算量小,无需进行双线性运算,因此参考其无双线性对的特点,提出了无双线性对的无证书聚合签密方案并进行了理论分析。
1 相关基础
1.1 离散对数问题
离散对数问题(Discrete Logarithm Problem,DLP):设G是q阶循环群,q为素数。给定两个元素P,Q∈G,找到使Q=nP成立的整数n。
1.2 聚合签密方案的安全模型
文献[4]定义的安全模型,无证书聚合签密方案将面临A1和A2两类敌手的攻击。
A1类敌手不知道系统的主密钥,但可以进行公钥替换操作,或利用所有用户的公钥来对系统主密钥进行攻击,因此A1类敌手为恶意用户。A2类敌手已知系统主密钥,具有计算所有用户部分公钥私钥的能力,但不可以替换用户公钥,因此A2类敌手为恶意的KGC。
选择密文攻击下的机密性和适应性,选择消息攻击下的不可伪造性。方案机密性证明中,U1是A1类敌手的挑战者,U2是A2类敌手的挑战者,不可伪造性证明中,T1是A1类敌手的挑战者,T2是A2类敌手的挑战者。文献[14]详细介绍了无证书聚合签密方案在A1和A2两类敌手适应性选择消息攻击下不可伪造性的定义及相应游戏,不再叙述。
定义1:类型A1攻击下的密文机密性。类型A1的攻击者不能在多项式时间内,以不可忽略的优势赢得以下博弈,则该签密方案在选择密文攻击下具有不可区分性。
SETUP:挑战者U1将生成的系统公共参数发送给敌手A1并保存系统主密钥。
第一阶段:敌手能够多项式次执行的询问如下:
部分密钥生成问询:A1输入(IDi,Xi)进行问询,就可得到(yi,Yi)。
私钥生成问询:A1输入IDi问询,得到SKi=(xi,yi)。

签密问询:A1输入(IDi,mi,IDB)问询,得到:
δi=(V,Vi,Si,Wi)=Signcryption(IDi,mi,IDB)
解签密问询:A1输入签密δi和身份(IDi,IDB)问询,U1可进行解签密,将解签密结果返回A1。
挑战阶段:A1选择要挑战的两个明文mi(i∈{0,1})和两个身份IDi,IDB,不能在第一阶段询问IDB的私钥。U1选择一个随机的比特b,计算δ*=Signcryption(mb,IDi,IDB),将δ*发送A1。
第二阶段:类似于第一阶段,A1能够多项式次执行询问,并且不能询问用户IDB私钥或对δ*进行解签密询问。
猜测阶段:最后A1提交一个比特b',若b'=b,那么A1在此游戏中获胜。游戏中敌手的优势为Adv[A1]=|Pr[b'-b]-0.5|。
定义2:类型A2攻击下的密文机密性。类型A2的攻击者不能在多项式时间内,以不可忽略的优势赢得以下博弈,则该签密方案在选择密文攻击下具有不可区分性[15]。
SETUP:挑战者U2将生成的系统公共参数发送给敌手A2并保存系统主密钥。
第一阶段:敌手可适应性地进行以下多项式数量级的询问:部分密钥生成问询、私钥生成问询、签密问询、解签密问询与定义1的问询一样,由A1问询变成A2问询,但不进行公钥替换询问。
第二阶段:类似于第一阶段,A2能够多项式次执行询问,并且不能询问用户IDB的私钥或对δ*进行解签密询问。
猜测阶段与定义1中类似,最终A2获胜。
2 基于离散对数问题的聚合签密方案
无证书聚合签密由7个算法组成,分别是系统初始化、用户密钥设置、部分私钥提取、签密、聚合签密和聚合解签密。

用户密钥设置:用户ui随机选取秘密值xi,计算公开参数Xi=xiP。

签密:用户ui对发送给IDB的消息mi签密如下:
(2)计算hi2=H2(IDi‖mi,V,Zi);
(3)计算Ti=H3(Vi,IDB,V,aiXB);
(4)计算Wi=Ti⊕(mi‖IDi),Si=ai+(xi+yi)hi2。这样δi=(V,Vi,Si,Wi)为ui对IDB消息mi的签密。

解签密:IDB对ui发送的签密δi=(V,Vi,Si,Wi)的解签密步骤如下:
(1)计算Ti=H3(Vi,IDB,V,xBVi),IDi‖mi=Wi⊕Ti;
(2)计算Zi=ai(YB+Ppubhi1)=yBVi,hi1=H1(IDi,Xi,Yi),hi2=H2(IDi‖mi,V,Zi);
(3)根据等式SiP=Vi+(Xi+Yi+Ppubhi1)hi2进行检测,若正确输出对应消息mi‖IDi,否则验证失败。

(1)计算Ti=H3(Vi,IDB,V,xBVi),IDi‖mi=Wi⊕Ti;
(2)计算Zi=ai(YB+Ppubhi1)=yBVi;

3 安全性分析
3.1 正确性
方案的正确性证明如下:
通过SiP=Vi+(Xi+Yi+Ppubhi1)hi2对签密进行验证:
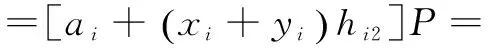


3.2 安全性


询问阶段:敌手A1进行下述询问:
H1查询:当A1向预言机H1询问H1(IDi,Xi,Yi)时,T1进行下述操作:
①如果列表L1中存在相应的元组

H2查询:当A1向预言机H2询问H2(IDi‖mi,V,Zi)时,T1进行下述操作:
①如果列表L2中存在相应元组

H3查询:当A1向预言机H3询问H3(Vi,IDB,V,aiXB)时,T1进行下述操作:
①如果列表L3中存在相应的元组

部分密钥生成询问:当A1要对IDi和公开参数Xi进行部分密钥生成询问时,T1进行如下操作:
①若Lk中存在相应元组
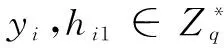
私钥生成询问:当A1要对IDi的私钥生成执行问询时,T1进行如下操作:
①如果列表Lsk中存在元组

公钥生成询问:当A1要对身份IDi的公钥生成执行询问时,T1进行下述操作:
①如果Lpk中存在元组


签密询问:当T1收到A1关于发送方身份、消息、接收方身份
①如果IDi=IDj,则T1放弃,终止模拟;

聚合签密询问:当T1收到A1关于发送方身份、消息、接收方身份

②否则T1弃权,停止模拟。
解签密问询:当T1收到A1关于发送者身份、接收者身份、签密
①倘若L1中存在IDi所对应的元组且IDi≠IDj,按照解签密算法进行解密,并验证SiP=Vi+(Xi+Yi+Ppubhi1)hi2是否成立,若成立T1返回1给A1,否则返回0;
②如果L1中存在IDi所对应的元组且IDi=IDj,则当L2中存在IDi相对应的元组
③如果L1中不存在IDi所对应的元组,则当L2中存在IDi对应的元组

①如果对于所有的IDi(1≤i≤n),都有IDi≠IDj,就将模拟中止。

①如果成立,则T1输出

作为离散对数问题的有效解;
②否则,T1没有解决离散对数问题。



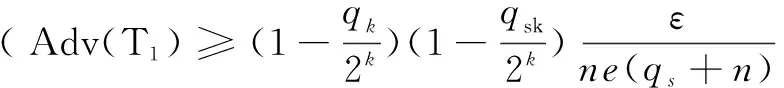


询问:敌手A2对预言机H1,H2,H3,私钥生成,公钥生成,签密和解签密的询问过程与引理1相同。
部分密钥生成询问:当A2执行对IDi和公开参数Xi的部分密钥生成询问时,T1进行如下操作:
①如果列表Lk中存在相应元组
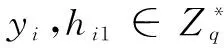
解签密问询:当T2收到A2关于发送者身份,接收者身份,签密
①若L1中存在IDi对应的元组且IDi≠IDj,则按解签密算法进行解密,并验证SiP=Vi+(Xi+Yi+Ppubhi1)hi2是否成立,如果成立,则T2返回1给A2,否则返回0。
②如果L1中存在IDi所对应的元组且IDi=IDj,则当L2中存在IDi相对应的元组

①如果对所有IDi都有IDi≠IDj,终止模拟。

如果等式成立,则T2输出:

作为离散对数问题的有效解;否则,T2没有解决离散对数问题。
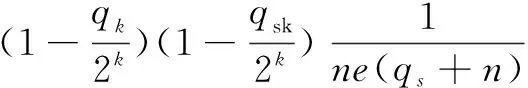
引理3:在随机预言模型下,若不存在任何多项式数量级的敌手A1在下面的游戏中能以不可忽略优势获胜,那么称该方案具有机密性。

询问:敌手A1询问过程与引理1相似。
第一阶段,A1或许产生两个长度相等的消息mi0,mi1来接受挑战。随机选择并通过执行签密算法获得ui对发送给IDB的关于消息mib的签密和聚合签密{δi,δ},返回δ*给敌手A1。

结束时,猜想A1被返回,若等式成立,则输出1;否则,输出0。由于敌手A1不能进行解签密询问,应用
引理4:在随机预言模型下,若不存在任何多项式数量级的敌手A2在下面的游戏中能以不可忽略优势获胜,那么称该方案具有机密性。

询问:敌手A2询问过程与引理2相似。
在第一阶段和第二阶段与引理3模拟类似,不同的是这里Zi=yBVi,yB是接收者的部分密钥,并且yB=b+shi1,YB=bP,Zi=ai(YB+Ppubhi1)=yBVi,则有b=(Vi)-1ai(YB+Ppubhi1)-shi1。由于离散对数问题中计算n是困难的,因此已知Zi和Vi求取b也是困难的。
3.3 效率分析
表1是上述方案与文献[6,9,17-18]的签密方案进行性能比较的结果。耗时比较大的计算主要有双线性对运算、幂运算和数乘运算,d表示双线性运算,h表示指数运算,t代表G上的点乘运(由于其他方案都使用了双线性运算,因此将群G记为G1,G2,G2为G1的双线性映射)。

表1 签密方案运算量比较
表1分析了5种聚合签密方案的运算量,点乘运算对比对运算和指数运算耗时少许多。文中方案签密者只需2次点乘运算,而文献[9,17-18]都需要进行双线性对运算,文献[9]在签密时运算量较小,但解签密时高于文中方案。文献[6]的指数运算较大,且其在解签密阶段比文中方案多了许多双线性运算和指数运算。因此文中方案较为高效。
4 结束语
为提高无证书聚合签名和无证书签密方案的有效性和安全性,在随机预言模型具有可证安全性的基础上,提出了无双线性对的聚合签密方案。该方案基于离散对数难题,避免了双线性对运算。由于离散对数难题至今未能解决,因此该方案更为安全可靠。在签密者人数不止一个的情况下,提高了签密和解签密的计算效率。
[1] Zheng Y.Digital signcryption or how to achieve cost (signature & encryption)≪cost (signature)+cost (encryption)[C]//Annual international cryptology conference.Berlin:Springer,1997:165-179.
[2] Selvi S S,Vivek S S,Shriram J,et al.Identity based aggregate signcryption schemes[C]//International conference on progress in cryptology-indocrypt.[s.l.]:[s.n.],2009:378-397.
[3] 祁正华.基于身份的签密方案研究[D].南京:南京邮电大学,2012.
[4] 于 刚.若干签密方案研究[D].郑州:解放军信息工程大学,2012.
[5] Ren Xunyi,Qi Zhenghua,Yang Geng.Provably secure aggregate signcryption scheme[J].ETRI Journal,2012,34(3):421-428.
[6] 苏爱东,张永翼.密文长度固定的全聚合签密方案[J].计算机应用研究,2015,32(9):2820-2822.
[7] Riyami S A,Paterson K.Certificatless public key cryptography[C]//Proceedings of the ASIACRYPT.Berlin:Springer-Verlag,2003:452-473.
[8] Barbosa M,Farshim P.Certificateless signcryption[C]//Proceedings of ASIACCS.Tokyo,Japan:ACM Press,2008:369-372.
[9] 陆海军.聚合签名与聚合签密研究[D].杭州:杭州师范大学,2012.
[10] Eslami Z,Nasrollah P.Certificateless aggregate signcryption:security model and a concrete construction secure in the random oracle model[J].Journal of King Saud University Computer and Information Sciences,2014,26(3):276-286.
[11] Qi Zhenghua,Yang Geng,Ren Xunyi.Provably secure certificateless ring signcryption scheme[J].China Communications,2011,8(3):99-106.
[12] QI Zhenghua,Ren Xunyi,Yang Geng.Provably secure general aggregate signcryption scheme in the random oracle model[J].China Communications,2012,9(11):107-116.
[13] 周彦伟,杨 波,张文政.高效可证安全的无证书聚合签名方案[J].软件学报,2015,26(12):3204-3214.
[14] Zhang L,Qin B,Wu Q H,et al.Efficient many-to-one authentication with certificate-less aggregate signatures[J].Computer Networks,2010,54(14):2482-2491.
[15] 高键鑫,吴晓平,秦艳琳,等.无双线性对的无证书安全签密方案[J].计算机应用研究,2014,31(4):1195-1198.
[16] 王大星,腾济凯.可证明安全的基于身份的聚合签密方案[J].计算机应用,2015,35(2):412-415.
[17] Han Yiliang,Chen Fei.The multilinear mapsbased certificateless aggregate signcryption scheme[C]//International conference on cyber-enabled distributed computing and knowledge discovery.[s.l.]:[s.n.],2015:92-99.
[18] Liu Jianhua,Zhao Changxiao,Mao Kefei.Efficient certificateless aggregate signcryption scheme based on XOR[J].Computer Engineering and Applications,2016,26(3):176-186.
A Certificateless Aggregate Signcryption Scheme without Bilinear Pairing
WANG Meng-shu,QI Zheng-hua
(School of Computer Science and Technology,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
Certificateless aggregate signcryption scheme can aggregate different signcryptions generated by multi-users corresponding to various information into one signcryption,which can not only ensure the confidentiality and certification in information transmission but also reduce power dissipation.Therefore,it is applied in the multiple-to-single mode in large-scale distributed communication.Most aggregate signcryption schemes need computation of bilinear pairing with poor efficiency.For that,an efficient certificateless aggregate signcryption schemes without bilinear pairing is proposed,where disperse logarithm is employed in random oracle model to improve the original aggregate signature algorithm without bilinear pairing for safer and more effective one.Based on the proposed aggregate signcryption security model,investigation and analysis on the presented scheme with random oracle model is performed and validation on its effectiveness and feasibility also conducted.Theoretical analysis shows that in the presence of multiple signcrypter it owns not only the confidentiality and unforgeability but also higher computational efficiency.
certificateless aggregate signcryption;random oracle model;without bilinear pairing;discrete logarithm problem
2016-09-01
2016-12-07 网络出版时间:2017-07-05
国家自然科学基金资助项目(61073188)
王梦殊(1993-),女,硕士研究生,研究方向为网络与信息安全;祁正华,副教授,博士研究生,研究方向为网络与信息安全。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170705.1651.048.html
TP301
A
1673-629X(2017)08-0115-06
10.3969/j.issn.1673-629X.2017.08.024
