基于散乱数据的二元样条)曲面重构方法
2017-09-01汪春晓
汪春晓,路 游
(中国石油大学(北京),北京 102249)
汪春晓,路 游
(中国石油大学(北京),北京 102249)
在计算几何领域中,利用曲面拟合散乱数据点集,是计算机图形学以及计算机辅助几何设计中一个困难的问题。传统的基于均匀2-型三角剖分的二元样条曲面重构算法存在重构速度较慢、曲面精度不高等问题。针对上述问题,提出了一种新的曲面重构方法。该方法通过数据点构造以卷积形式表示的控制系数,并构造迭代公式,迭代计算数据点与曲面的距离,根据距离调整控制系数,直到前后两次数据点到曲面的最大距离的差值小于适当的阈值,进而确定最佳的控制系数,通过将点置于数据块中,以数据块为单位进行计算,采用取整的方式消除边界处的重复计算,减少了重构曲面的计算次数。实验结果表明,该方法提高了曲面重构的速度和质量,证明了此方法是可行、有效的。
二元样条;卷积;曲面重构;控制系数;迭代方法
0 引 言
样条函数,是具有一定光滑性的分段或者分片定义的多项式函数。在计算机几何领域与飞机、船舶制造等领域均有重要的应用。一元样条应用最早、最广泛,研究的最详细的是3次样条函数。1946年,数学家I.J.Schoenberg系统地建立了一元样条函数的理论基础[1]。从60年代开始,样条函数有了迅速的发展和应用。1966年,H.B.Curry和I.J.Schoenberg提出了一元B样条函数,是一种定义B样条函数的几何直观方法[2]。1975年,利用函数论和代数几何方法,王仁宏教授构建了多元样条函数的基本理论框架,开创了一套研究多元样条函数基本问题的新方法,即光滑余因子协调法[3]。目前在多元样条的研究方法上大致可分为三类:光滑余因子协调法,以王仁宏为代表;B-网方法,以Farin[4]为代表;B-样条方法,亦称投影子法,以Schoenberg[2]、de Boor[5]和Micchelli[6]等为代表。最近一段时间,样条函数方面也有许多研究成果。文献[7-8]分别介绍了多元样条的应用研究,B样条在模糊系统中的应用,等等。在文献[9-13]分别介绍了B样条的图像插值方法,B样条的数值流形和时间积分方法。
曲线曲面造型是计算机图形学、计算机辅助几何设计和计算机辅助设计所研究的重要内容,多元样条在其中有重要的作用。到目前为止,曲线曲面造型以逐渐形成了以非均匀有理B样条设计和隐式代数曲面为主体,以插值、拟合、逼近等方法为骨架的理论体系[3,14]。传统的基于均匀2-型三角剖分二元样条曲面重建方法构造的曲面具有内置的连续性,重建后的曲面整体次数低,控制顶点相对较少,曲面拼接时无需考虑拼接处的光滑问题,同时,曲面也具有良好的几何和逼近性质,如几何不变性、变差缩减性等。但是,该方法也存在一些不足,比如重构曲面的速度较慢,数据点与重构曲面之间的距离过大等。
针对以上问题,提出了一种新的非张量积型二元样条曲面重构方法,通过卷积形式表示控制系数,结合数据点得到初始的控制系数,并构造迭代公式,迭代计算数据点与拟合曲面的距离,根据距离重新调整控制系数,直到前后两次数据点到曲面的最大距离的差值小于给定阈值,最后通过最佳的控制系数进行曲面重构。
1 算法基本原理
1.1 均匀2-型三角剖分上二元样条函数空间
均匀2-型三角剖分是在矩形剖分的基础上,连接其中各小矩形的两条对角线而形成的三角剖分,如果矩形剖分是均匀剖分的,那么,形成的均匀2-型三角剖分也是贯穿剖分[15]。
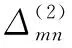
mx-i=0,ny-i=0,ny-mx-i=0,ny-mx-
i=0
其中,i=…,-1,0,1,…。

图1 区域D及其剖分
每个内网点均由四条直线相交而成,如式(1)所示[16]:
Ni>(k+1)/(k-μ)
(1)
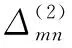
k>(4μ+1)/3
(2)
当μ一定时,则要求多项式的次数尽可能低,那么可以得到如下若干个均匀2-型剖分上的样条函数空间:
利用贯穿剖分上的样条函数空间维数公式[16]:
(3)



图2 区域Q及其剖分
对各i=1,2,…,25,剖腔上的多项式可表示为:
根据对称性原则可以推出其他剖腔上的多项式。
记Β(x,y)为图2中定义在Q上的分片多项式,在编号为i的剖腔上记为pi,那么显然Β(x,y)C1(2),并且在Q内部Β(x,y)>0。因此,Β(x,y)是上的样条函数,并且由文献[17-18]可知,Β(x,y)的支集是最小的。
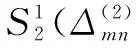
(4)
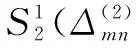
由式(4)定义的二元样条函数A满足:
(5)
对任意的i0,j0,0≤i0≤m+1,0≤j0≤n+1,集合Ai0,j0={Bi,j(x,y)A:(i,j)≠(i0,j0)},构成了样条函数空间的一组基底。
A中的二元样条函数具有如下性质:
(6)
1.3 构造拟插值算子
(1)港口岸线资源整合和港区功能布局优化,推进港口集约化发展。由于码头性质、经营等方面的原因,杭州港存在着泊位利用效率不高,岸线使用效益差,部分港区功能布局分散等现象。本次港口总体规划的编制,将按照岸线资源利用集约化和港口发展规模化、大型化和专业化的要求对岸线资源进行整合利用,对港区和泊位功能进行调整。总体规划中处理好既有泊位与规划新建泊位的关系,实现港口岸线资源整合和港区功能布局优化将是杭州港总体规划编制工作的难点之一。
(7)
(8)
(9)


(10)
对于以上两种拟插值算子有以下结论[17]:
(11)
1.4 优化控制系数
由控制系数表达式(见式(10))可知,控制系数与每一个数据块周围的四个数据点以及中心点的值有关,如图3所示。

图3 四个数据点及中心点



(12)
由于初始控制系数矩阵是预估值,会存在偏差,所以要对其进行修正。
E:=S-F
(13)

(14)
1.5 划分边界点
由式(9)可知,曲面W(f)由λi,j(f)和Bi,j(x,y)决定,由式(4)可知,Bi,j(x,y)是由B(x,y)在水平和垂直方向上进行平移得到,并且最终得到的曲面的定义域I⊂2。
需要对∀(x,y)2定义其所属的块编号(i,j),(i,j)∈2,如图4所示。令:
(⎣x」,⎣y」)=(i,j),(x,y)(⎣x」,⎣y」)
(15)

图4 边界处点划分方法
这样,∀(x,y)∈2都有唯一的编号。可记为:{(⎣x」,⎣y」)|∀(x,y)∈[1,m+1)×[1,n+1),m,n∈}={(⎣x」,⎣y」)|∀(x,y)∈[1,m]×[1,n],m,n∈}。
2 算法实现过程
输入:给定数据点集F,阈值τ,数据点距离曲面最大距离e1,前一次的数据点距离曲面最大距离e0。


步骤4:在曲面上取与给定数据点坐标相同的点,根据式(13)计算其与给定数据点之间的最大距离ek,令e1=ek。
步骤6:输出曲面W。
通过推导和分析可知,当输入点为m×n时,总计算时间为Θ(l×m×n),其中l为迭代次数,与曲面结构有关。
3 实验结果
用Matlab软件在处理器为Intel-1.80 GHz,内存为4.0 GB的普通个人电脑上分别利用传统非张量积型曲面重构方法和文中提出方法进行曲面重构,结果如图5所示。

(a)原始曲面

(b)在原始曲面上获取的数据点

(c)传统)方法重构出的曲面

(d)利用文中方法重构出的曲面
曲面重构各参数如表1所示。

表1 曲面重构数据参数表
4 结束语
针对传统的非张量积型二元样条曲面重构速度较慢、曲面精度不高等问题,提出新的非张量积型二元样条曲面重构方法,通过重新构造控制系数,并利用迭代公式不断修正控制系数,进而得到符合要求的最佳控制系数,使得重构出的曲面质量得到提高。在重构过程中,划分点与块的归属关系,将原来计算点的过程转化为计算块的过程,并且降低边界处点的重复运算,减少了计算次数,降低了运算量,从而提高了重构曲面的速度。最后通过实验证明了文中方法的可行性。
[1] Schoenberg I J.Contribution to the problem of application of equidistant data by analytic functions[J].Quart. Appl. Math,1946,4:45-99.
[2] Curry H B,Schoenberg I J.On Polya frequency functions IV:the fundamental spline functions and their limits[J].J. Analyse Math,1996,17:71-107.
[3] 王仁宏.多元齿的结构与插值[J].数学学报,1975,18(2):91-106.
[4] Farin G.Bezier polynomials over triangles and the construction of piecewise Cr polynomials[R].Brunel:University of Uxbridge,Middlesex,1980.
[5] de Boor C.Spline as linear combination of B-spline[M]//Approximation theory II.New York:Academic Press,1976:1-47.
[6] Dahmen W,Micchelli C A.Recent progress in multivariate splines[M]//Approximation Theory IV.New York:Academic Press,1983.
[7] 郭庆杰.多元样条若干理论与应用研究[D].大连:大连理工大学,2015.
[8] 谭彦华,李洪兴,马秀娟,等.B样条函数在模糊系统中的应用[J].控制理论与应用,2013,30(11):1445-1456.
[9] 魏晓静.基于B样条函数的图像插值方法研究[D].大庆:东北石油大学,2014.
[10] 温伟斌.基于B样条插值的数值流形方法与时间积分方法的研究[D].重庆:重庆大学,2014.
[11] Zeng Xiaoming,Zhou Guorong,Yang Lianqiang.Best bounds on the distance between 3-direction quartic box spline surface and its control net[J].Applied Mathematics:A Journal of Chinese Universities,2013,28(2):147-157.
[12] 杨联强,王 东.三向四次箱样条曲面与Bezier曲面的光滑拼接[J].计算机工程与应用,2013,49(23):119-121.
[13] Fang Meie,Lu Jia,Peng Qunsheng.Volumetric data modeling and analysis based on seven-directional box spline[J].Science China:Information Science,2014,57(6):1-14.
[14] 施法中.计算机辅助几何设计与非均匀有理B样条:CAGD&NURBS[M].北京:北京航空航天大学出版社,1994.
[15] 王仁宏,崔锦泰.关于一个二元B样条基[J].中国科学,1984(9):12-23.
[16] Chui C K,Wang R H.Multivariate spline spaces[J].Jour. Math.Anal. Appl.,1983,94:197-221.
[17] 王仁宏,施锡泉,罗钟铉,等.多元样条函数及其应用[M].北京:科学出版社,1994.
[18] Wang R H.The dimension and basis of spaces of multivariate splines[J].Journal of Computational and Applied Mathematics,1985,12(85):163-177.

WANG Chun-xiao,LU You
(China University of Petroleum,Beijing 102249,China)
In the field of computation geometry,the use of surface fitting scattered data points is a difficult problem for CG and CAGD.The traditional bivariate spline surface reconstruction algorithm based on uniform type-2 triangulation exists shortcomings of slow speed and poor accuracy.Aiming at these problems above,a new surface reconstruction method is developed successfully.The convolution type control coefficient is offered through the data points,and the distance between data points and surface is obtained by iterative method.Then according to the distance,control coefficient is adjusted until the difference is less than the appropriate threshold before and after the maximum distance of data points and surface,so the optimum control coefficient is determined.Then blocks are selected as basic calculation unit,eliminating repeated calculation at the boundary reduced computation times.The results show that the method improves the speed and quality of surface reconstruction and is proved to be feasible and effective.
bivariate spline;convolution;surface reconstruction;control coefficient;iteration method
2016-08-27
2016-11-30 网络出版时间:2017-06-05
国家自然科学基金资助项目(60873093)
汪春晓(1991-),男,硕士生,研究方向为计算机可视化、计算几何;路 游,博士,副教授,研究方向为计算几何、图形学、虚拟现实。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170605.1508.052.html
TP391
A
1673-629X(2017)08-0025-05
10.3969/j.issn.1673-629X.2017.08.006
