基于改进广义导抗法的独立电力系统静态稳定性分析

胡 健 付立军 王 刚 马 凡

(舰船综合电力技术国防科技重点实验室(海军工程大学) 武汉 430033)

基于改进广义导抗法的独立电力系统静态稳定性分析

胡 健 付立军 王 刚 马 凡

(舰船综合电力技术国防科技重点实验室(海军工程大学) 武汉 430033)

系统稳定性是独立电力系统设计和运行时需要被重点考虑的因素。由于现有稳定性判据的保守性，使得独立电力系统在设计时为保证稳定运行而付出了更多代价，对电力电子装置级联的条件提出了更严格的限制。为此提出同时考虑增益裕度约束和相位裕度约束的改进广义导抗稳定性分析方法，推导了具有更小禁止域的稳定性判据，用以计算多运行点系统的电源广义阻抗约束集和负载广义导纳集。以某同步整流发电机带恒功率负载的独立电力系统为例，验证了所提出的稳定性分析方法的正确性。与现有方法相比，该方法有效降低了保守性，提高了分析精度。

独立电力系统 整流发电系统 恒功率负载 稳定性分析

0 引言

独立电力系统是指与大电网隔离独立运行的电力系统，近年来在船舶、混合动力汽车、海岛等电力系统中得到广泛应用[1-5]。独立电力系统中通常含有变频调速的电动机系统，它被认为是一类恒功率负载，具有负阻抗特性，这是导致独立电力系统失稳的主要原因[6，7]。此外，电力电子装置级联是独立电力系统的另一个特征。虽然级联系统中各电力电子装置在设计时能确保独自运行时的稳定，但是它们级联后由于输入输出阻抗的不匹配，容易导致级联系统失稳[8-11]。因此在设计和分析独立电力系统时，需要重点关注系统的静态稳定性。另一方面，由于独立电力系统运行存在多种运行点的情况[12-16]，系统电压、频率、负载功率等常在一定的范围内变化，运行点往往不是确定值，因此需要研究有异于单一运行点系统的稳定性分析的方法。

在独立电力系统稳定性分析方法中，目前主流的方法是通过计算级联系统源输出阻抗(Zs)和负载输入导纳(Yl)乘积的奈奎斯特曲线，来判断系统稳定性[17]。Middlebrook判据[18]是最简单的一种系统稳定性判定方法，根据Middlebrook输入输出阻抗判据，当系统的ZsYl奈奎斯特曲线全部位于单位圆内时，系统是稳定的。因此在已知源输出阻抗(或负载导纳)时，可以计算得出负载约束导纳(或源约束阻抗)，反之亦然。然而，Middlebrook判据按照满足所有相位裕度约束的前提下，只考虑了增益裕度约束，因此在奈奎斯特平面中除了单位圆内部的区域外，其他区域均为禁止域，具有严重的保守性；增益相角判据[19]和相对论证判据[20，21]可以降低稳定性分析结果的保守性，但是由于数学求解形式复杂，且容易受源和负载组成形式的影响，使其很少在实际的独立电力系统中得到应用。能量源联合分析判据[22-24](Energy Source Analysis Consortium,ESAC Criterion)在GMPM判据禁止域基础上进行改进，定义了新的更小的禁止域，大大减小了稳定性分析方法的保守性并简化了判据的复杂程度，因此是目前导抗稳定性分析方法中首先选用的一种稳定性判据。当系统存在多个不同的运行点时，建立源输出广义阻抗和负载输入广义导纳，通过选择合适的导抗稳定性判据，建立广义负载输入导纳约束集或者源输出阻抗约束集，分析独立系统在多运行点下的静态稳定性。

本文在现有广义导抗法ESAC稳定性判据基础上，首先将原有相位裕度约束和增益裕度约束分开考虑的过程改为同时考虑相位裕度约束和增益裕度约束对奈奎斯特平面禁止域的影响，得到含更小禁止域的改进稳定性判据；再根据源广义输出阻抗集和改进的稳定性判据，计算具有更小保守性的负载输入导纳约束集，根据负载输入导纳约束集与广义负载输入导纳集判断系统稳定性；最后以某三相同步交流发电机接不控整流装置带恒功率负载的独立电力系统为例，验证本文方法与现有方法相比有效改善了保守性，并得到更为准确的结果。

1 小环增益曲线和ESAC判据

1.1 小环增益曲线

对于一个独立电力系统，通过戴维南等效将其等效为一个源-负载系统，如图1所示。

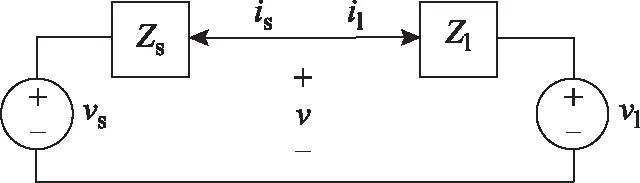
图1 戴维南等效源-负载电路Fig.1 The Thevenin equivalent source-load circuit

图1中vs为戴维南等效电势，Zs为源阻抗，vl为等效负载电压，Zl为负载阻抗。对于端口电压v有

(1)

定义Zs和Zl为

(2)

则式(1)可以改写为

(3)

根据奈奎斯特理论，当负载稳定运行的时候，Nl不存在位于右半平面的零点，同样当电源带恒功率负载稳定运行时，Ds不存在位于右半平面的零点。对式(3)进行变形，得到

(4)

式中，Yl为负载导纳，Yl=1/Zl。将ZsYl的奈奎斯特曲线称为小环增益曲线[22-24]。因为Nl和Ds在右半平面不含有零点，所以当1+ZsYl右半平面不存在零点时，系统是稳定的。小环增益曲线在s平面上，不包含(-1，j0)的点。

1.2 ESAC稳定性判据

独立电力系统含有多运行点的特点，使得单一运行点的稳定性分析方法不能全面反映独立电力系统的稳定性，因此需要研究广义稳定性。广义导抗稳定性分析需要根据系统不同运行点形成源输出广义阻抗和负载输入广义导纳[25]。再根据源输出广义阻抗计算负载输入导纳约束集，或者根据负载输入广义导纳计算源输出阻抗约束集。

最为主要的步骤是选择合适的稳定性判据来计算导纳和阻抗约束集。稳定性判据定义原则是确保小环增益曲线不包含s平面上(-1，j0)的点。目前广义稳定性分析方法中，广泛使用的稳定性判据是ESAC稳定性判据。

ESAC稳定性判据禁止域由两部分组成，第一部分边界是平行于实轴的两条直线，始于负无穷，与单位圆相交于相位裕度约束在s平面上与单位圆的交点。其中相位裕度约束曲线为两条与负实轴夹角为±PM的直线[22-24]，ESAC稳定性判据禁止域如图2所示。表达式为

(5)式中，PM为相位裕度；∠x= angle(Re(x)+jIm(x))，∠x∈(-π，π]，加法运算的结果以2π为周期映射到区间(-π，π]中。ESAC稳定性判据的禁止域第二部分边界是增益裕度约束与负实轴交点(-1/GM，j0)，与单位圆上交点的连线，增益裕度约束方程为

(6)

式中，GM为增益裕度，dB。

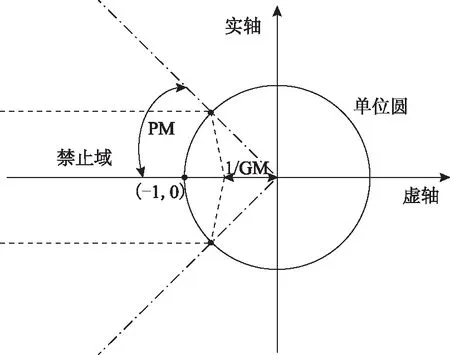
图2 ESAC稳定性判据Fig.2 ESAC stability criterion

稳定性判据边界曲线包含(-1，j0)点的区域为禁止域。与其他稳定性判据相比较，ESAC判据具有更小的禁止域，允许小环增益曲线在s平面上有更大的稳定区域。

2 改进的广义导抗稳定性分析方法

2.1 稳定性判据

为尽可能减小稳定性判据的保守性，需要将禁止域边界在可能的范围内进一步缩小，通过幅值增益约束和相位裕度约束的相互限制减小禁止域，使得小环增益曲线可以在相平面上更大的范围内出现，从而改善稳定性判据保守性。

在ESAC稳定性判据的基础上，当确定禁止域第一部分边界时，考虑±PM的相角约束，同时考虑增益裕度约束1/GM的影响，将第一部分平行实轴直线与圆的交点，由原先在单位圆上，改为半径为1/GM的圆上，其中GM≥1。改进法禁止域平行实轴的第一部分边界数学表达式为

(7)

为避免因考虑增益裕度约束后，禁止域第二部分边界包含更多区域，改进法禁止域第一部分边界与第二部分边界的交点为改进法平行线与ESAC判据的交点，与负实轴仍然交于(-1/GM，j0)点，改进法禁止域的第二部分边界数学表达式为

(8)

改进的稳定性判据禁止域如图3所示。

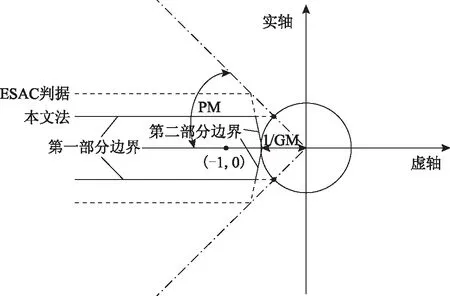
图3 改进的稳定性判据Fig.3 Improved stability criterion

当在相同的相位裕度PM约束下，改进法具有比ESAC判据更小的禁止域，保守性得到了改善，且增益裕度GM越大，改善效果越明显，GM=1 dB时，两者是重合的，所以ESAC判据是改进法在GM=1 dB时的一种特殊情况。当在相同的增益裕度GM约束下，改进法能得到比ESAC判据更小的禁止域，PM接近0°时两种方法保守性一样，当PM=90°时，保守性改善效果最明显。

2.2 负载广义导纳约束集

如图4所示，在s平面上绘制稳定性判据禁止域边界曲线和源输出阻抗曲线。由前文已知若小环增益曲线不能包含点(-1，j0)，则系统稳定，根据稳定性判据，即不进入禁止域内。

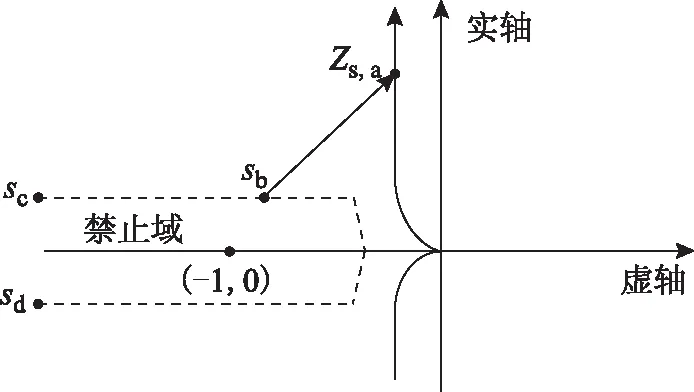
图4 单个频率下广义约束集计算Fig.4 The generalized constraint set under a single frequency

选定某一频率点fa，Zs，a为该频率下源输出阻抗奈奎斯特曲线上的值。点sb为位于稳定性判据禁止域边界曲线上的点，当小环增益曲线触及禁止域边界时，负载约束导纳有

(9)

当源输入阻抗已知时，将点sb沿sc到sd的方向在整条边界上移动时计算得到在频率点fa处的负载输入导纳约束，Yl，ab在幅值-相角平面上为一闭合曲线。将源输出阻抗奈奎斯特曲线上的值由频率点fa扩大至整个频域或者某段感兴趣的范围，就得到了以频率、相角和幅值为坐标轴的三维广义负载输入导纳约束集。

2.3 广义稳定性分析

对于像不确定系统或时变系统等具有多个平衡状态点的系统，例如当发电机端角频率在0.9(pu)～1.1(pu) 范围内变化，均分选取10个状态点，负载端功率在0.8(pu)～1.2(pu)变化，均分取10个状态点。利用传统稳定性分析方法，就有100种运行点需要计算。若利用广义稳定性分析方法，可以在三维空间坐标系中，一次性完成稳定性分析，这样就避免了传统稳定性分析方法重复计算的过程。

在三维空间中，以x轴为频率对数，单位是Hz，y轴是相角，单位是°，z轴是幅值增益，单位是dB，建立三维空间导纳/阻抗坐标系。可用凸等角多边形法[25]或其他数学方法确定含有多运行点系统在固定频率时的源输出阻抗范围曲线，扩展至整个频域范围建立三维源输出广义阻抗集。再结合稳定性判据和求取广义约束集方法，计算负载输入导纳约束集。通过判断源输出广义阻抗集空间和广义约束集空间在三维坐标系中是否存在重叠的部分判断系统是否稳定，若不存在重叠部分，表明在整个频域范围内小环增益曲线不包含(-1，0)的点，系统是稳定的。

广义稳定性分析方法与传统稳定性方法相比，其优势在于处理多运行状态点的情况，但对于有固定运行平衡点的电力系统稳定性分析同样适用，此时就变为判断三维空间中两条曲线是否有交点。

3 算例验证

3.1 算例系统模型简化

图5为某三相同步发电机整流带恒功率负载电力系统结构，将图5所示系统看作是电源整流子系统和恒功率负载子系统的级联。

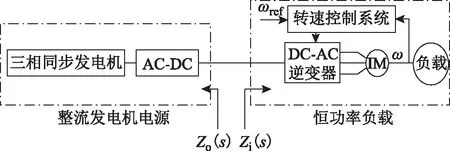
图5 三相同步发电机整流带恒功率负载电力系统Fig.5 Three phase synchronous generator rectifier power system with constant power load

对于电源整流子系统，可将其等效为如图6所示电路。

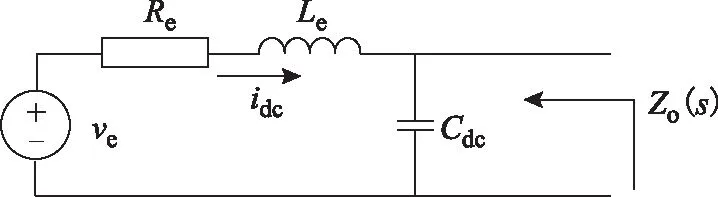
图6 电源整流子系统等效电路图Fig.6 Equivalent circuit diagram of electrical commutator system

小信号输出阻抗Zo(s)可以表示为

(10)

式中，Le、Re、Cdc分别为等效直流电感、电阻和电容，Le=Lt+Ldc，Ldc为直流侧电感，Lt≈L″q+L″d，Re=3ωrLc/π+2r，r为电枢电阻，ωr为电机角频率，Lc≈(L″q+L″d)/2。

对于恒功率负载子系统中的电动机，其等效电路如图7所示。

图7 恒功率负载子系统等效电路Fig.7 Constant power load subsystem equivalent circuit

小信号输入阻抗Zi(s)为

(11)

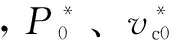
因此图5所示系统的简化结构如图8所示，其中各部分参数见表1。

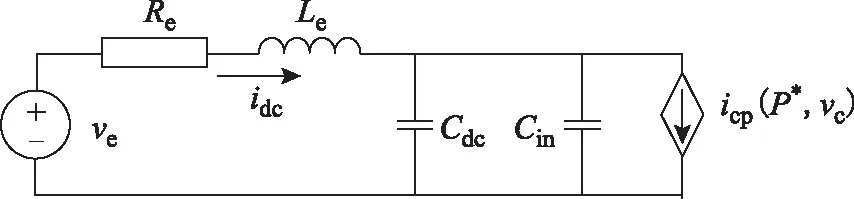
图8 简化电力系统结构Fig.8 Simplify the power system structure

参数数值电源等效电势ve/V500电源等效电阻Re/Ω0.9842电源等效电感Le/mH7.1345电源直流侧电容Cdc/mF1.5负载输入电容Cin/mF2恒功率负载P/kW25

3.2 算法对比

采用保守性较小且目前广泛使用的ESAC算法作为本文改进算法的对比。

首先，在计算源输出广义阻抗时，输入电压按额定值的80%～120%均分选取10个值，发电机角频率按额定值的80%～120%均分选取10个值，共100个运行点，用凸等角多边形法确定固定频率下多运行点的边界，扩展至频域范围建立源输出广义阻抗。同理计算负载输入广义导纳时，输入电压按额定值的80%～120%均分取5个值，负载功率按15～25 kW均分取10个值，共50个运行点，建立负载输入广义导纳。结果如图9、图10所示。

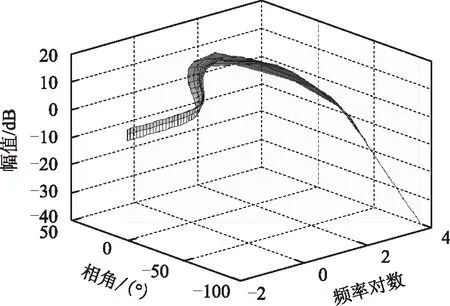
图9 源输出广义阻抗Fig.9 Generalized output impedance of source

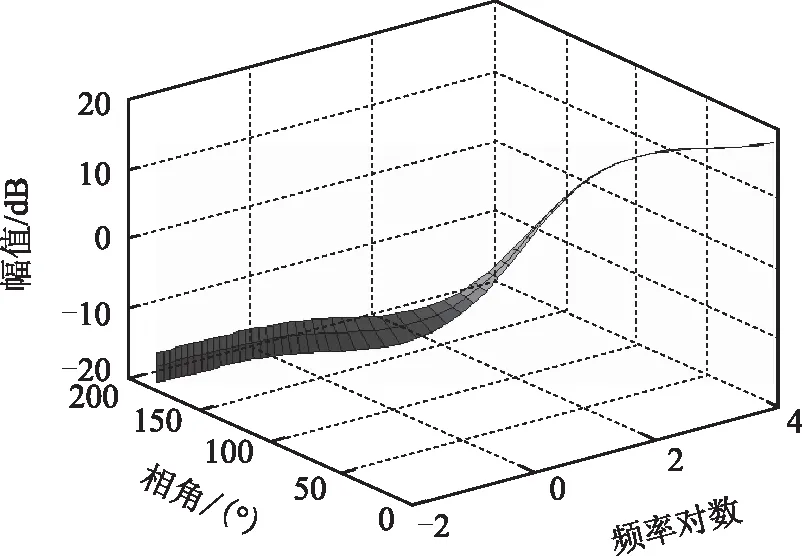
图10 负载输入广义导纳Fig.10 Generalized input admittance of load

利用源输出广义导抗，分别采用ESAC判据和本文方法计算负载输入导纳约束集。图11为在响应频率为100 Hz时两种方法所得约束集边界对比，可以看出因保守性的差异，ESAC法禁止域要大于本文方法。图12和图13为在0.01 Hz到10 kHz频率范围内的稳定性分析结果。

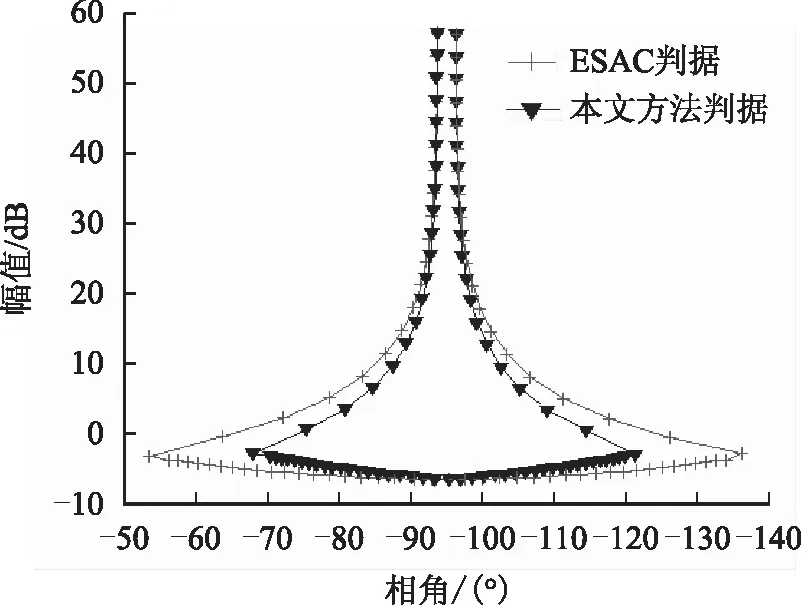
图11 100 Hz响应频率处约束集边界对比Fig.11 Constraint set of boundaries at 100 Hz frequency

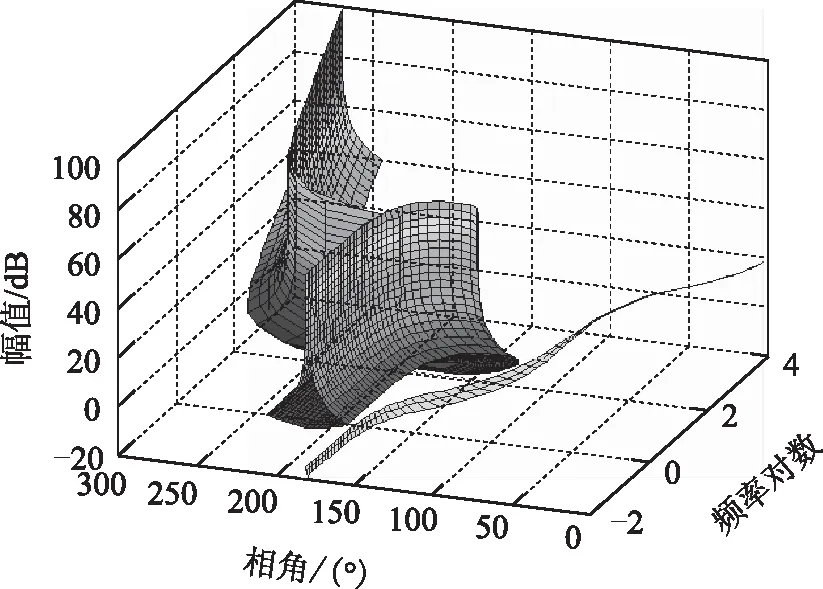
图13 本文方法稳定性分析Fig.13 Improved method for stability analysis

图12中，在100 Hz处，所有运行点组成的负载输入广义导纳均与负载输入导纳约束集发生了交叉，且交叉部分包含所有运行的状态点，因此，不能表明系统是稳定的，在工程设计经验上往往根据这种判断结果，将系统认定是不稳定的。

图13中所有运行点组成的负载输入广义导纳与负载输入导纳约束集未交叉，表明系统稳定。

从图12和图13可以看出，因为保守性的差异，ESAC稳定性判据和本文改进判据得到的结果不同。在Matlab/Simulink中，建立图8所示独立电力系统的电磁暂态仿真模型，仿真得到系统在表1所示参数运行点下，恒功率负载侧的直流电压和直流电流波形如图14、图15所示。

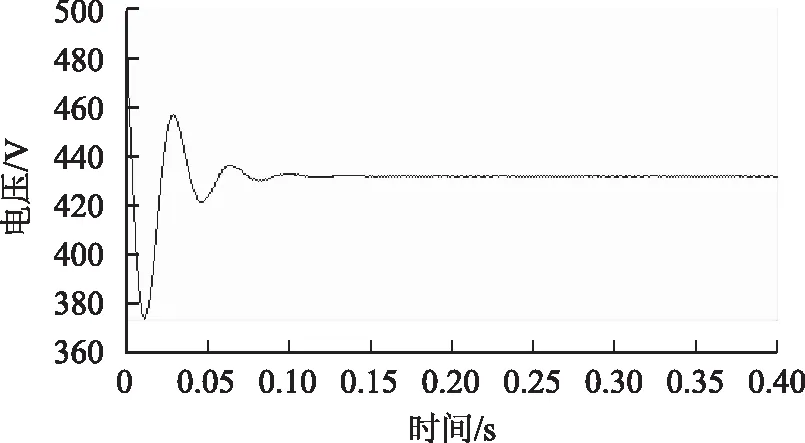
图14 恒功率负载输入电压仿真波形Fig.14 The input voltage’s simulation waveform of constant power load

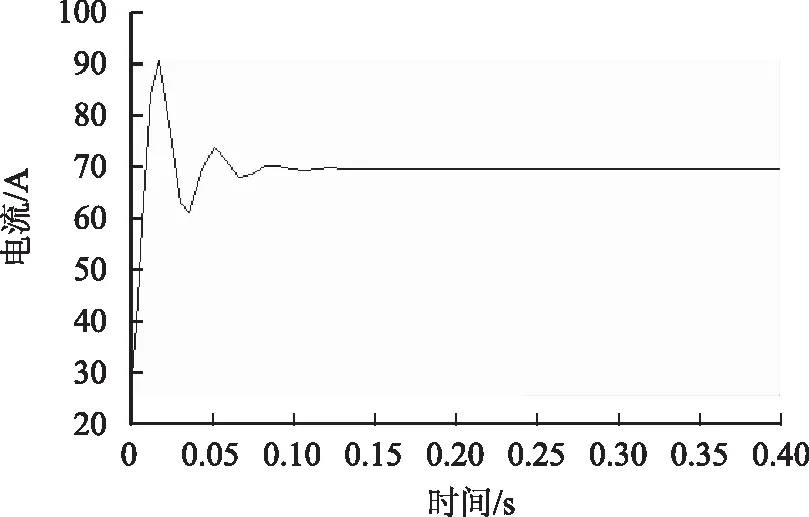
图15 恒功率负载输入电流仿真波形Fig.15 The input current’s simulation waveform of constant power load

通过图14、图15可以看出，系统能够稳定运行，说明本文方法分析的结果是正确的，表明本文方法能够有效地减小广义导抗稳定性分析方法的保守性。

对于不稳定的系统，根据稳定性理论，系统的小环增益曲线一定包含相平面上(-1，j0)的点。而ESAC判据和本文方法，点(-1，j0)都位于禁止域内，根据约束集求解方法可知约束集一定会和广义集发生交叉，所以本文方法在减小保守性的同时，不会出现将不稳定的系统误判为稳定的情况。

4 结论

本文为减小现有广义导抗稳定性分析方法的保守性，在ESAC判据的基础上，通过同时考虑相位裕度约束和增益裕度约束，在s平面上确定禁止域边界，得到了更小的禁止域。并考虑参数动态变化对系统稳定性的影响，将传统稳定性分析拓展至广义的稳定性分析，提出了基于改进广义导纳法的稳定性分析方法，与现有的广义导抗稳定性分析方法相比：

1)由于本文方法稳定性判据具有更小的禁止域，因此能得到保守性更小的负载输入导纳约束集或源输出阻抗约束集，提高了准确分析系统稳定性的能力。

2)系统设计时，在s平面上为小环增益曲线提供了更大的可行域，降低了对级联系统的稳定性设计要求和成本。

实际工程中的独立电力系统相比算例更加复杂，但是可以通过戴维南等效对各发电机、换流器、负载等单独计算阻抗，再根据网络串并联拓扑最终等效为源-负载系统，因此本文稳定性分析方法对于多机多负载系统同样适用。

本文方法能够为独立电力系统稳定性设计提供指导，并适合含多运行点电力系统稳定性分析。

[1] 杨新法，苏剑，吕志鹏，等.微电网技术综述[J].中国电机工程学报，2014，34(1)：57-70. Yang Xinfa，Su Jian，Lü Zhipeng，et al.Overview on micro-grid technology[J].Proceedings of the CSEE，2014，34(1)：57-70.

[2] 吴卫民，何远彬，耿攀，等.直流微网研究中的关键技术[J].电工技术学报，2012，27(1)：98-106. Wu Weimin，He Yuanbin，Geng Pan，et al.Key technologies for DC micro-grids[J].Transactions of China Electrotechnical Society，2012，27(1)：98-106.

[3] 陈丽丽，牟龙华，刘仲.光储柴微电网运行特性分析[J].电力系统保护与控制，2015，43(12)：86-91. Chen Lili，Mu Longhua，Liu Zhong.Analysis of the operating characteristics of a PV-Diesel-BESS microgrid system[J].Power System Protection and Control，2015，43(12)：86-91.

[4] 沈沉，吴翔宇，王志文，等.微电网实践与发展思考[J].电力系统保护与控制，2014，42(5)：1-11. Shen Chen，Wu Xiangyu，Wang Zhiwen，et al.Practice and rethinking of microgrids[J].Power System Protection and Control，2014，42(5)：1-11.

[5] 张颖，容展鹏，张宇雄，等.基于微电网的电网需求响应研究[J].电力系统保护与控制，2015，43(21)：20-26. Zhang Ying，Rong Zhanpeng，Zhang Yuxiong，et al.Study of grid demand response based on micro grid[J].Power System Protection and Control，2015，43(12)：20-26.

[6] 付立军，刘鲁锋，王刚，等.我国舰船中压直流综合电力系统研究进展[J].中国舰船研究，2016，11(1)：72-79. Fu Lijun，Liu Lufeng，Wang Gang，et al.The research progress of the medium voltage DC integrated power system in China[J].Chinese Journal of Ship Research，2016，11(1)：72-79.

[7] 赵雷廷，刁利军，董侃，等.地铁牵引变流器-电机系统稳定性控制[J].电工技术学报，2013，28(6)：101-107. Zhao Leiting，Diao Lijun，Dong Kan，et al.Stabi-lization control for metro traction converter-motor system[J].Transactions of China Electrotechnical Society，2013，28(6)：101-107.

[8] 杜韦静，张军明，张阳，等.DC-DC变流器带恒功率负载动态响应分析及级联系统稳定性预测[J].电工技术学报，2011，26(1)：83-90. Du Weijing，Zhang Junming，Zhang Yang，et al.Transient load response analysis of DC-DC converter with constant power load and stability prognosis of cascaded system[J].Transactions of China Electrotechnical Society，2011，26(1)：83-90.

[9] 杜韦静，张军明，钱照明.Buck变流器级联系统直流母线电压补偿控制[J].电工技术学报，2015，30(1)：83-90. Du Weijing，Zhang Junming，Qian Zhaoming.Compensation methodology for DC bus voltage of cascaded system formed by Buck converters[J].Transactions of China Electrotechnical Society，2015，30(1)：83-90.

[10]范学鑫，马伟明，付立军，等.电力电子变换器级联系统阻抗全系统算法[J].海军工程大学学报，2013，25(3)：19-24. Fan Xuexin，Ma Weiming，Fu Lijun，et al.Input-output impedance computing method for whole system of cascaded power electronic devices[J].Journal of Naval University of Engineering，2013，25(3)：19-24.

[11]贾鹏宇，李艳，郑琼林.电压型级联系统中减小源变换器输出阻抗的有源阻尼控制方法[J].电工技术学报，2015，30(8)：71-82. Jia Pengyu，Li Yan，Zheng Trillion Q.An active damping method to reduce output impedance of converters in voltage source cascaded system[J].Transactions of China Electrotechnical Society，2015，30(8)：71-82.

[12]肖定垚，王承民，曾平良，等.电力系统灵活性及其评价综述[J].电网技术，2014，38(6)：1569-1576. Xiao Dingyao，Wang Chengmin，Zeng Pingliang，et al.A survey on power system flexibility and its evaluations[J].Power System Technology，2014，38(6)：1569-1576.

[13]韩冬，马进，贺仁睦，等.负荷模型不确定性对电力系统动态仿真的影响[J].中国电机工程学报，2008，28(19)：69-74. Han Dong，Ma Jin，He Renmu，et al.Effect of uncertainty in load model on power system dynamic simulation[J].Proceedings of the CSEE，2008，28(19)：69-74.

[14]刘胜，程垠钟.基于多维gPC 的船舶电力推进系统仿真不确定性分析[J].电工技术学报，2016，31(2)：128-135. Liu Sheng，Cheng Yinzhong.Uncertainty analysis for simulation of shipboard electric propulsion system based on multi-dimensional gPC[J].Transactions of China Electrotechnical Society，2016，31(2)：128-135.

[15]于东，孙欣，高丙团，等.考虑风电不确定出力的风电并网协调优化模型[J].电工技术学报，2016，31(9)：34-41. Yu Dong，Sun Xin，Gao Bingtuan，et al.Coordinated optimization model for wind power integration considering wind power uncertainty output[J].Transactions of China Electrotechnical Society，2016，31(9)：34-41.

[16]赵书强，王明雨，胡永强，等.基于不确定理论的光伏出力预测研究[J].电工技术学报，2015，30(16)：34-41. Zhao Shuqiang，Wang Mingyu，Hu Yongqiang，et al.Research on the prediction of PV output based on uncertainty theory[J].Transactions of China Electrotechnical Society，2015，30(16)：34-41.

[17]Riccobono A，Santi E.Comprehensive review of stability criteria for DC distribution systems[C]//Energy Conversion Congress and Exposition，2012：3917-3925.

[18]Middlebrook R D.Input filter considerations in design and application of switching regulators[C]//IEEE IAS Annu，1976：366-382.

[19]Wildrick C M，Lee F C，Cho B H，et al.A method of defining the load impedance specification for a stable distributed power system[J].IEEE Transactions on Power Electron，1996，10(3)：280-285.

[20]Feng Xiaogang，Ye Zhihong，Xing Kun，et al.Impedance specification and impedance improvement for DC distributed power system[C]//30thIEEE Power Electronics Specialists Conference，1999，2：889-894.

[21]Feng Xiaogang，Liu Jinjun，Lee F C.Impedance specifications for stable DC distributed power systems[J].IEEE Transactions on Power Electronics，2002，17(2)：157-162.

[22]Sudhoff S D，Glover S F，Lamm P T.Admittance space stability analysis of power electronic systems[J].IEEE Transactions on Aerospace & Electronic Systems，2000，36(3)965-973.

[23]Sudhoff S D，Glover S F.Three-dimensional stability analysis of dc power electronics based system[C]//IEEE Power Electronics Specialists Conference，2000，1：101-106.

[24]Suryanarayana H，Sudhoff S D.Refinements in generalized immittance based stability analysis of DC power electronics based distribution systems[C]//Electric Ship Technologies Symposium，2015：80-85.

[25]Sudhoff S D，Loop B P，Byoun J，et al.A new procedure for calculating immittance characteristics using detailed computer simulations[C]//IEEE Power Electronics Specialists Conference，2007：901-908.

(编辑 赫蕾)

Steady-State Stability Analysis of Isolated Power System Based on Improved Generalized Immittance Method

HuJianFuLijunWangGangMaFan

(National Key Laboratory of Science and Technology on Vessel Integrated Power System Naval University of Engineering Wuhan 430033 China)

Stability is an important element to be considerated in the design and analysis of isolated power system. Due to the conservatism of the existing stability criterion, which makes the isolated power system cost a lot for stable operation. Tighter restrictions are also put forward for system cascade. In this paper, consider the gain margin and phase margin constrain at the same time and deduce the stability criterion with smaller forbidden region to calculate generalized impedance constraint set and generalized load admittance set of the multi operating point system. An isolated power system consisting of a synchronous machine with a rectifier as a source and a constant power as load is analyzed by using the proposed method and which compared with existing method shows it can get more accurate results and reduced conservatism effectively.

Isolated power system，rectifier generation system，constant power load，stability analysis

10.19595/j.cnki.1000-6753.tces.160832

国家重点基础研究发展计划(973计划)(613294)和国家自然科学基金(51377167)资助项目。

2016-06-02 改稿日期2016-09-09

TM71

胡 健 男，1990年生，博士研究生，研究方向为电力系统稳定性分析与控制。

E-mail：417356933@qq.com(通信作者)

付立军 男，1967年生，教授，博士生导师，研究方向为电力系统设计与建模。

E-mail：Lijunfu2006@sina.cn