考虑定位力矩补偿的磁通切换永磁电机模型预测转矩控制方法
2017-08-31黄文涛
黄文涛 花 为 於 锋
(1.东南大学电气工程学院 南京 210096 2.南通大学电气工程学院 南通 226019)
考虑定位力矩补偿的磁通切换永磁电机模型预测转矩控制方法
黄文涛1花 为1於 锋2
(1.东南大学电气工程学院 南京 210096 2.南通大学电气工程学院 南通 226019)
为了减小定位力矩对磁通切换永磁(FSPM)电机性能的影响,提出了一种考虑定位力矩补偿功能的模型预测转矩控制(MPTC)方法。通过有限元分析获得FSPM电机定位力矩主要谐波的数学表达式,根据补偿控制理论,构建能够抵消定位力矩的补偿转矩模型。基于MPTC原理,利用补偿转矩模型、预测转矩模型和预测磁链模型共同设计价值函数,以获得最优开关状态。所提控制方法不但能实现定位力矩补偿和转矩脉动抑制,还具有较好的动态性能,并且适用于一般的永磁同步电机。仿真和实验结果验证了所提控制方法的有效性。
磁通切换永磁电机 定位力矩补偿 模型预测转矩控制 转矩脉动
0 引言
磁通切换永磁(Flux-Switching Permanent Magnet,FSPM)电机具有功率密度高、输出转矩大和反电动势正弦等优点,在新能源电动汽车和风力发电等领域被广泛应用[1-3]。
FSPM电机较高的气隙磁通密度与定转子双凸极结构会产生较大的定位力矩。定位力矩会引起电机运行时的转矩脉动、振动和噪声问题,从而降低了FSPM电机的性能及效率,并限制了其应用。很多学者对定位力矩进行了深入研究,目前关于定位力矩削弱的方法主要可分为两大类:一种是从电机本体设计角度对定位力矩进行优化,如辅助槽[4]、斜槽[5]、转子齿形状优化[6]、转子分段[7]等。此类方法能从根本上降低定位力矩,但会增加电机设计的难度与生产成本;另一种方法从控制角度,利用补偿控制的方法对定位力矩进行补偿,该方法可以在电机加工制作完成后,减小定位力矩对电机输出性能的影响[8,9]。文献[8]在q轴给定电流中附加补偿电流对理想定位力矩进行补偿,并在低速条件下验证了所提方法的有效性。文献[9]深入分析了FSPM电机定位力矩,并从转矩产生机理角度设计了补偿电流来补偿定位力矩。虽然这些控制策略都能有效补偿定位力矩,但其动态性能均未得到验证。
模型预测控制(Model Predictive Control,MPC)技术因其结构简单、动态性能优越,在电机驱动和控制领域被广泛应用[10-14]。MPC实现方式较多,其中有限控制集模型预测控制(Finite-Control-Set-MPC,FCS-MPC)受到了国内外学者深入地研究。根据控制变量的不同,FCS-MPC具体可分为有限控制集模型预测电流控制(Model Predictive Current Control,MPCC)和有限控制集模型预测转矩控制(Model Predictive Torque Control,MPTC)。MPCC以定子电流矢量为控制变量,通过对定子电流的约束来获得最优开关状态[13]。由于缺少对转矩的约束,当MPCC应用于永磁同步电机时,电机输出转矩易受定位力矩影响。MPTC以转矩和定子磁链幅值为控制变量,通过对二者的共同约束来获得最优开关变量,该方法能从一定程度上减小转矩脉动[15]。文献[16]将MPTC方法和占空比调制策略相结合,并将其应用到FSPM电机控制中,仿真结果表明该方法能降低逆变器开关频率和转矩脉动。然而,论文并未考虑定位力矩对电机性能的影响。
本文基于MPTC策略,提出一种补偿FSPM电机定位力矩的控制方法。首先,通过理论分析得到定位力矩的数学表达式;然后根据补偿控制策略,设计可抵消定位力矩的补偿转矩模型,并利用其与MPTC中的预测转矩和磁链模型共同构建价值函数,通过优化价值函数获得最优开关状态;最后利用仿真和实验验证了所提控制方法的稳态和动态性能。
1 三相12/10极FSPM电机
1.1 结构与特性
图1为一台三相12/10极FSPM电机的拓扑结构。该电机定、转子呈双凸极结构,转子上既无绕组也无永磁体,结构简单,适合高速运行。若将一块U形硅钢片导磁铁心和一片永磁体组成的部分称之为一个模块,则FSPM电机的定子部分是由12个模块依次紧贴拼装而成。每个U形导磁铁心围成的槽中并排放置了两个集中绕组线圈,12个线圈分成3组,每4个串联成一相。
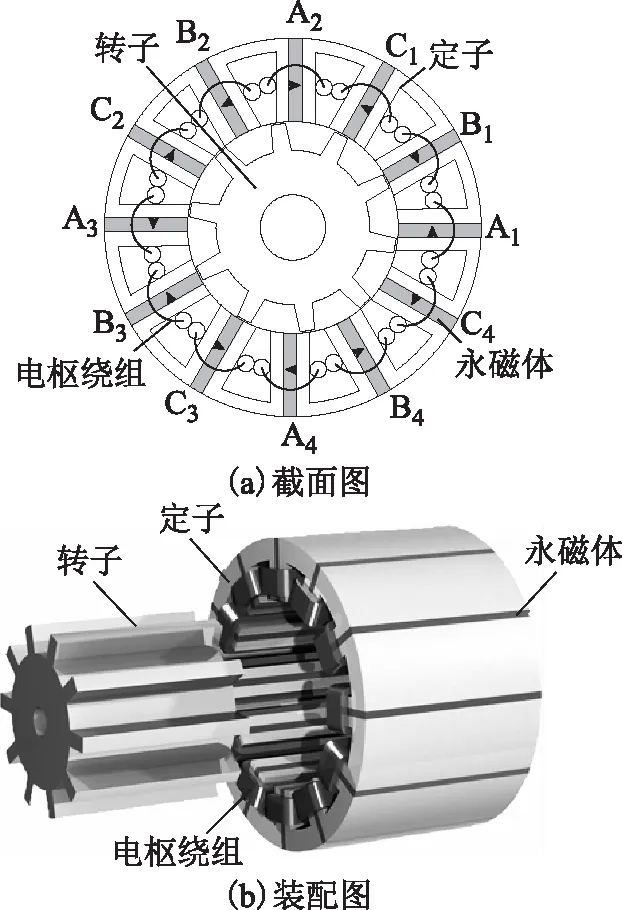
图1 三相12/10极FSPM电机结构Fig.1 Structure of three-phase 12/10 FSPM machine
图2a为额定转速(1 500 r/min)条件下FSPM电机的空载反电动势仿真波形,图2b为空载反电动势波形的快速傅里叶变换(Fast Fourier Transform,FFT)分析结果。仿真和分析结果表明,FSPM电机反电动势正弦度较好,总谐波失真(Total Harmonic Distortion,THD)较低。若忽略高次谐波,则可认为三相空载反电动势仅由基波分量构成,其可表示为
(1)
式中,Pr为转子极数;ωr为转子机械角速度;Em为反电动势基波幅值。
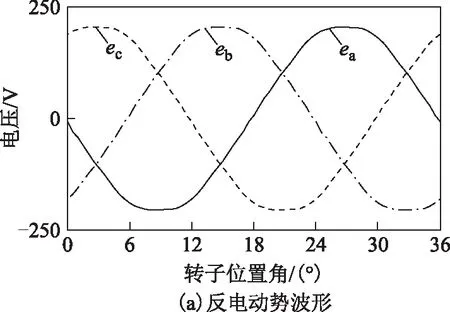
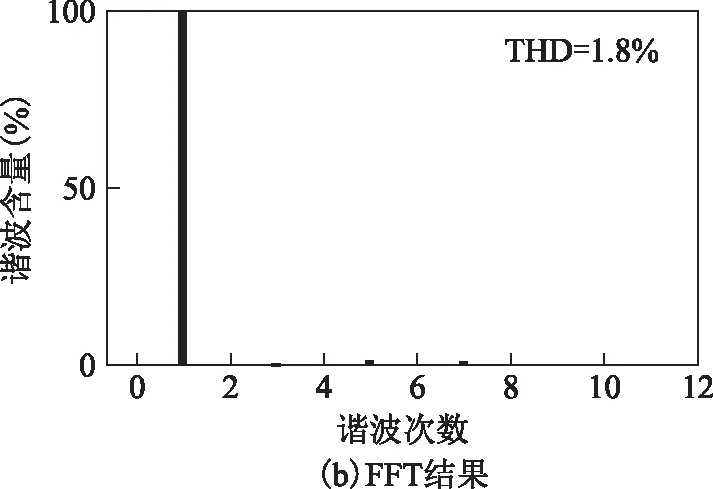
图2 空载反电动势Fig.2 Backelectromotive force at no load
1.2 定位力矩
在定子槽距范围内,FSPM电机定位力矩周期由电机的定子槽数和转子极数决定,其表达式为
(2)
式中,Ps为定子槽数;HCF为取Ps和Pr最大公约数。
对于本文中的三相12/10极FSPM电机,Np=5,则定位力矩周期可以机械角度表示为
(3)
采用有限元软件计算得到的定位力矩波形如图3所示,从图中可见定位力矩周期与理论计算值一致,定位力矩峰值为1.2 N·m,占额定转矩(13.38 N·m)的9%。仿真结果表明,该FSPM电机的定位力矩是关于转子位置的周期性函数。为得到定位力矩的数学表达式,利用FFT对定位力矩波形进行分析,结果见表1。定位力矩谐波含量较高,其中基波分量和2次谐波分量的幅值起主导作用。若忽略2次以上的高次谐波,则可得到FSPM电机定位力矩表达式为
(4)
式中,Tcmh为定位力矩谐波分量的幅值;θr为转子机械位置角;φcogh为定位力矩谐波分量相位角;h为谐波次数;M=2。
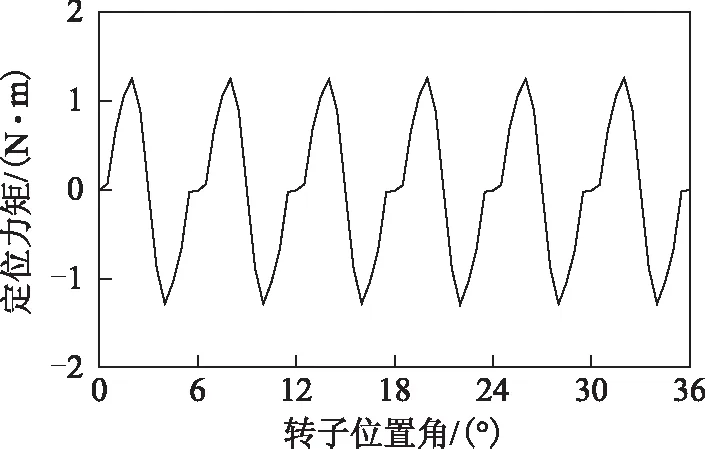
图3 定位力矩仿真波形Fig.3 Simulated waveform of the cogging torque
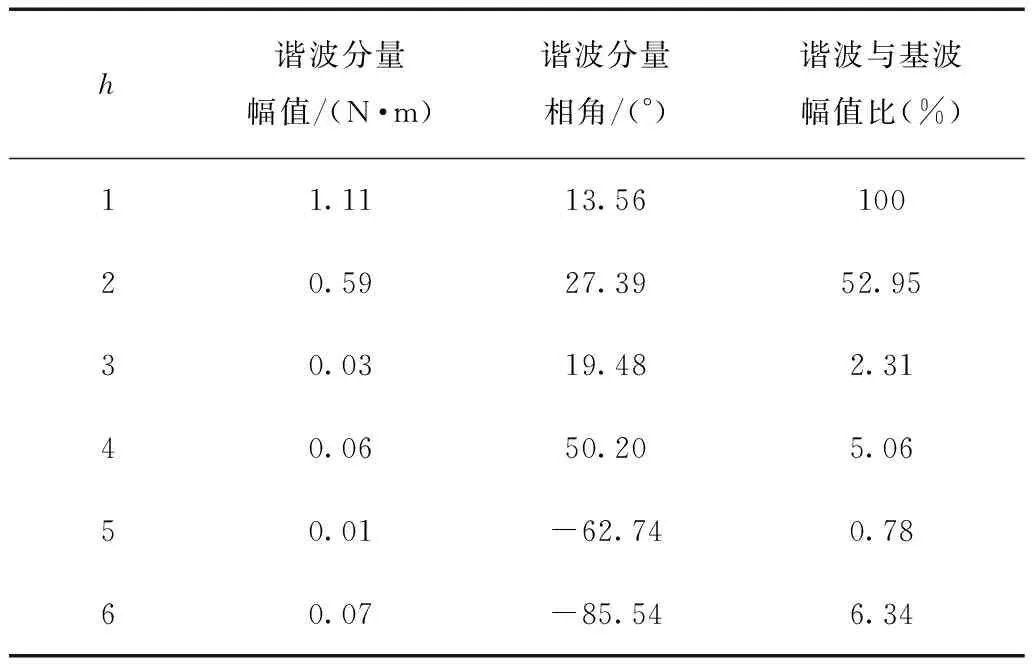
h谐波分量幅值/(N·m)谐波分量相角/(°)谐波与基波幅值比(%)11.1113.5610020.5927.3952.9530.0319.482.3140.0650.205.0650.01-62.740.7860.07-85.546.34
1.3 数学模型
d-q旋转坐标系中FSPM电机电流微分方程和磁链方程分别为
(5)
(6)
式中,ud、uq、id、iq、Ld、Lq、ψd和ψq分别为定子电压、电流、电感和定子磁链的d、q轴分量;Rs为定子电阻;ψf为永磁体磁链幅值。
FSPM电机电磁转矩Tem由永磁转矩Tpm、磁阻转矩Tr和定位力矩Tcog三部分组成,即
(7)
2 FSPM电机模型预测转矩控制
2.1 定子磁链参考计算
FSPM电机的磁链幅值参考并不是一个定值,其随负载转矩变化而变化。根据磁链自适应方法[17]和id=0的控制策略,定子磁链幅值参考表达式可表示为
(8)
2.2 预测模型
利用式(9)将FSPM电流微分方程式(5)进行离散化
(9)
可得到电流预测模型为
(10)
式中,Ts为采样时间;k和k+1分别为第k次采样和第k+1次采样。
将式(10)代入式(6)则可得到定子磁链预测模型为
(11)
从控制角度而言,定位力矩可视为FSPM电机的固有干扰,在构建预测转矩模型时,可暂不考虑。由永磁转矩和磁阻转矩分量构建的预测转矩模型为
(12)
2.3 定位力矩补偿
为了减小定位力矩对FSPM电机输出性能的影响,需要对定位力矩进行补偿。根据补偿控制思想[8,9],本文在获得定位力矩数学模型的基础上,通过直接注入与定位力矩幅值相同、相位相反的补偿转矩来抵消定位力矩,从而减小转矩脉动。根据1.2节中的定位力矩表达式,可构建补偿转矩模型为
(13)
2.4 价值函数
为了得到最优开关状态,根据所获得的预测磁链模型、预测转矩模型和补偿转矩模型设计价值函数。与传统的MPTC价值函数类似,需要有权值系数连接转矩和定子磁链幅值。本文所设计的价值函数为
(14)
式中,i={0,…,7};λ为定子磁链幅值的权值系数。考虑定位力矩补偿的FSPM电机MPTC策略结构如图4所示。
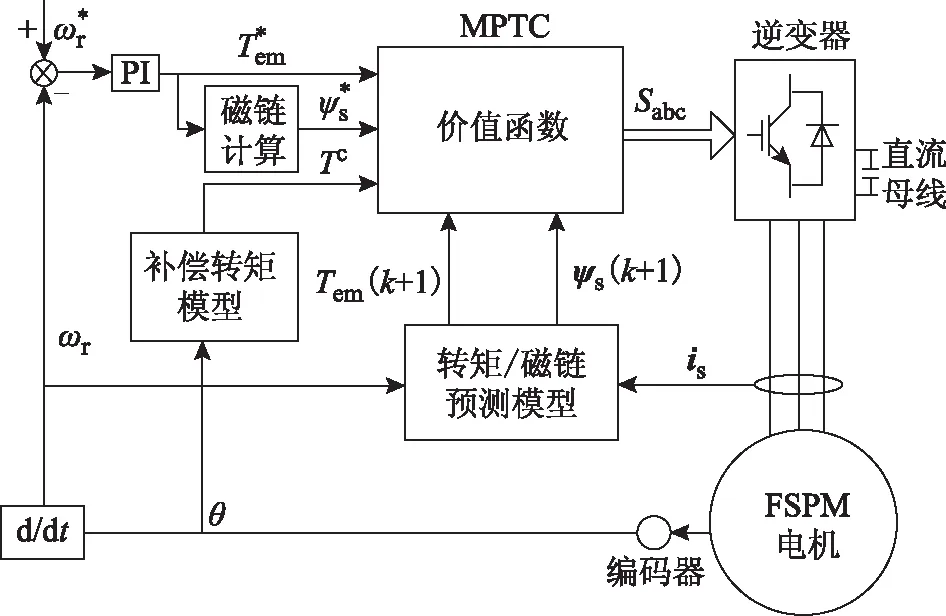
图4 考虑定位力矩补偿的FSPM电机MPTC策略Fig.4 MPTC scheme of FSPM machine with cogging torque compensation
3 仿真验证
在Matlab/Simulink环境中对图4所示的控制策略进行仿真验证,FSPM电机参数见表2。转速调节器参数为KP=0.01,KI=2,价值函数中的连接权值λ=150。图5为FSPM电机在600 r/min、5 N·m稳态条件下,补偿转矩模型作用前、后的仿真波形。从图中可以看出,补偿前,相电流谐波含量较低,其中A相电流THD约为9%,然而转矩受定位力矩影响,脉动较大,峰值达到1.8 N·m。补偿后,受补偿转矩作用,相电流谐波含量上升,其中A相电流THD约为18%,而转矩脉动明显降低,峰值约为1 N·m。稳态仿真结果表明,本文所提控制方法可有效补偿定位力矩,并降低转矩脉动。
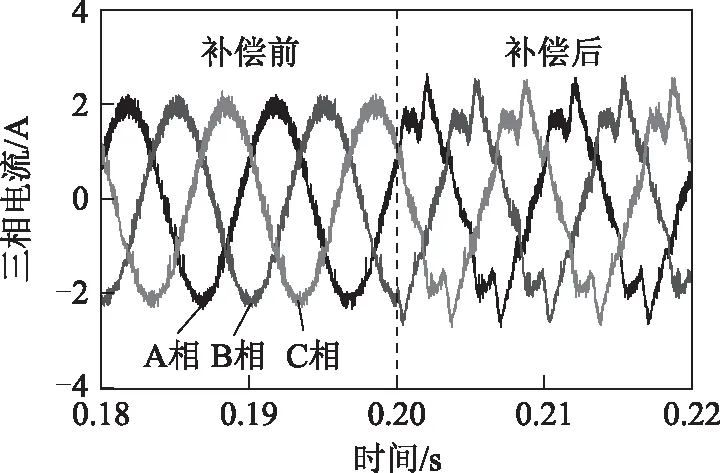
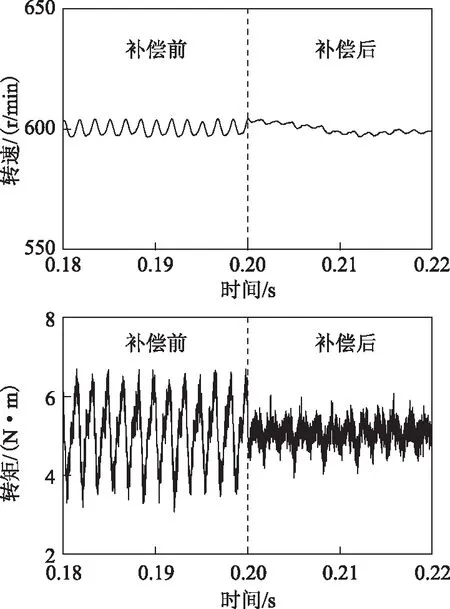
图5 本文所提控制策略稳态仿真波形Fig.5 Simulated waveforms of the proposed control scheme at the steady-state
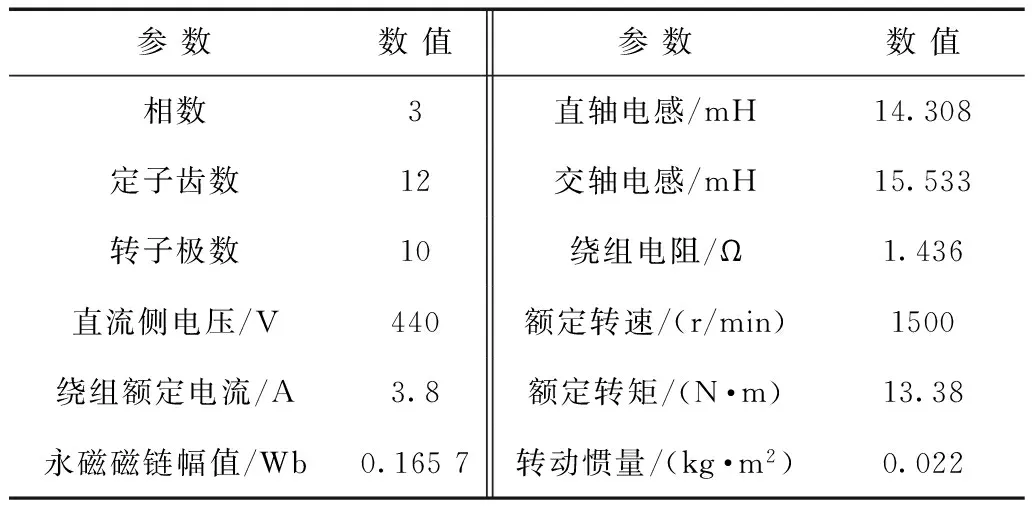
参数数值参数数值相数3直轴电感/mH14.308定子齿数12交轴电感/mH15.533转子极数10绕组电阻/Ω1.436直流侧电压/V440额定转速/(r/min)1500绕组额定电流/A3.8额定转矩/(N·m)13.38永磁磁链幅值/Wb0.1657转动惯量/(kg·m2)0.022
图6为本文所提控制方法的动态仿真波形。在t=0.25 s时,转速给定由600 r/min突变为-600 r/min。从图中可以看出,在本文所提控制方法作用下,FSPM电机相电流、转速和转矩响应较快,定位力矩补偿效果不受电机转速和负载变化影响。动态仿真结果表明本文所提控制方法具有较好的动态性能。
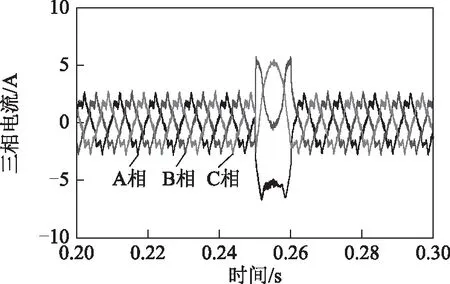
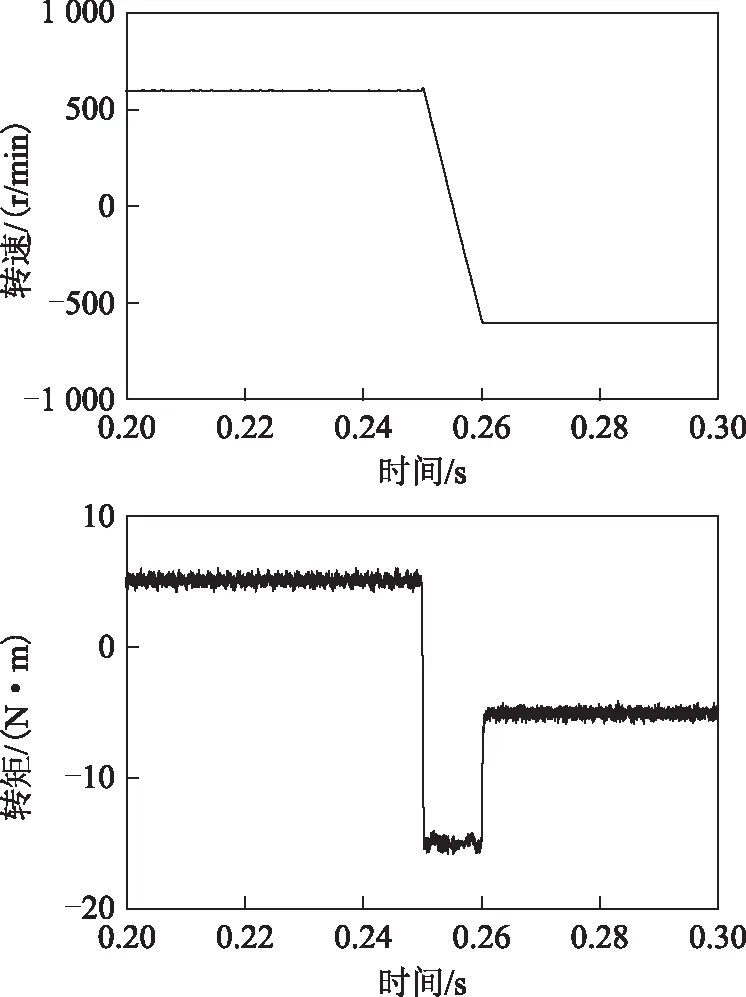
图6 本文所提控制策略动态仿真波形Fig.6 Simulated waveforms of the proposed control scheme at the dynamic-state
4 实验验证
为了进一步验证本文所提控制策略的有效性,在一台三相FSPM电机控制平台(如图7所示)上进行了实验验证。电机参数同仿真参数(见表2)。图7中,负载为磁粉制动器,三相电流和直流母线电压分别通过LEM霍尔传感器获得,转子位置信号通过2048线光电编码器得到。控制器采用dSPACE1104控制板,采样频率为10 kHz。转速调节器参数为KP=0.05,KI=0.4,价值函数中的连接权值λ=90。

图7 实验平台Fig.7 Experimental platform
图8为FSPM电机在600 r/min、5 N·m负载稳态条件下,补偿转矩模型作用前、后的输出波形。补偿转矩作用后,电流THD上升,且幅值有所增大,而转矩脉动明显降低,峰值由2 N·m降低为1.2 N·m。稳态实验结果与稳态仿真结果较为一致。
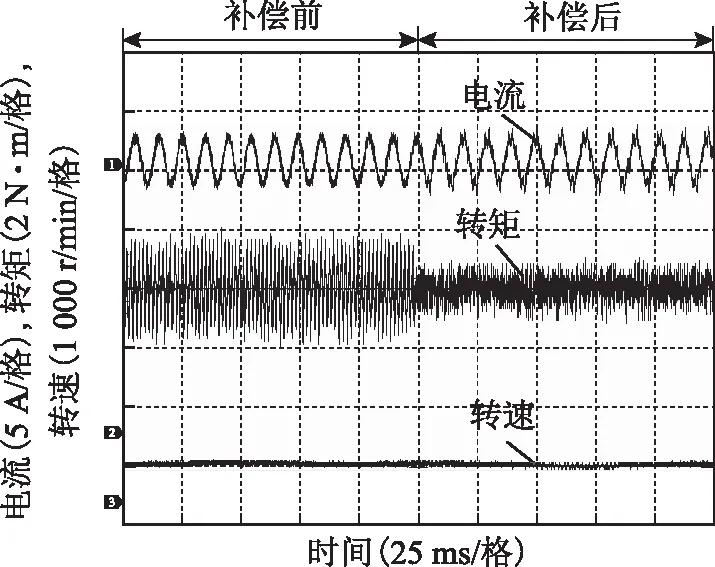
图8 稳态实验波形Fig.8 Experimental waveforms at the steady-state
图9为FSPM电机在本文所提控制策略作用下的起动响应曲线。电机由静止状态加速至600 r/min、4 N·m负载状态,经过100 ms,电流、转矩和转速均达到稳定。转矩脉动较低,为1.2 N·m。图10为FSPM电机在本文所提控制策略作用下的转速突变响应曲线。在6 N·m负载条件下,转速给定由600 r/min突变为-600 r/min,经过100 ms,转速达到稳定,定位力矩补偿效果不受转速变化影响,该结果与仿真结果一致。
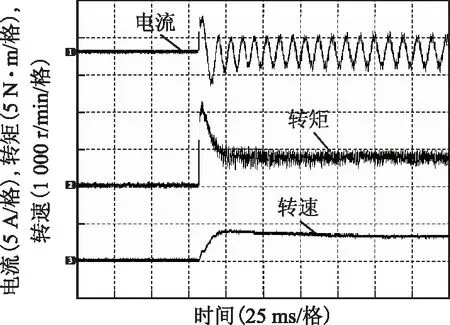
图9 起动响应Fig.9 Responses to startup
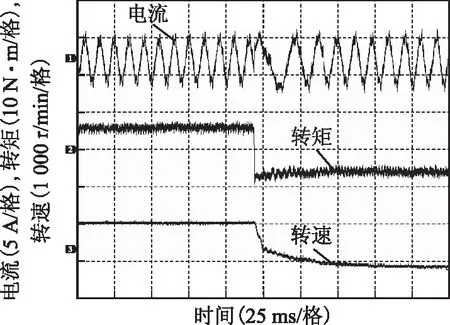
图10 转速突变响应Fig.10 Responses to speed step-change
图11为转速不变、负载变化条件下,FSPM电机响应曲线。由于磁粉制动器不能实现瞬态加载,故加载实验的响应时间长于转速突变实验的响应时间。图11中,转速保持600 r/min不变,负载转矩由2 N·m变为7 N·m,经过200 ms,负载转矩达到稳定,本文所提控制方法对定位力矩的补偿作用亦不受转矩变化影响。稳态和动态实验结果表明,本文所提控制方法不但能有效补偿定位力矩,降低转矩脉动,还具有较好的动态性能。
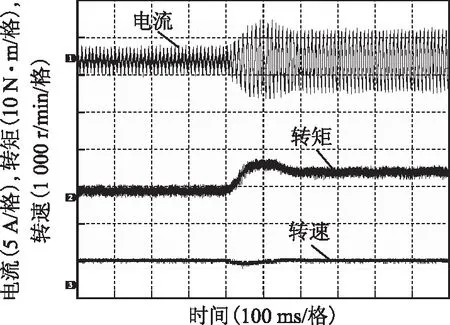
图11 负载变化响应Fig.11 Responses to the load change
5 结论
为了减小定位力矩对FSPM电机性能的影响,基于补偿控制思想和FCS-MPC策略,本文提出了一种考虑定位力矩补偿作用的MPTC方法,并对该方法的稳态和动态性能进行了仿真和实验验证。结果表明,所提出的控制方法通过引入补偿转矩,能有效补偿FSPM电机定位力矩并降低转矩脉动,同时还具有较好的动态性能。该方法为FSPM电机高性能控制提供了一种新思路,也为拓展FSPM电机的工程应用提供了一条新途径。
[1] 程明,张淦,花为.定子永磁型无刷电机系统及其关键技术综述[J].中国电机工程学报,2014,34(29):5204-5220.
Cheng Ming,Zhang Gan,Hua Wei.Overview of stator permanent magnet brushless machine systems and their key technologies[J].Proceedings of the CSEE,2014,34(29):5204-5220.
[2] Hua Wei,Cheng Ming,Zhang Gan.A novel hybrid excitation flux-switching motor for hybrid vehicles[J].IEEE Transactions on Magnetics,2009,45(10):4728-4731.
[3] Cheng Ming,Zhu Ying.The state of the art of wind energy conversion systems and technologies:a review[J].Energy Conversion and Management,2014,88:332-347.
[4] Hua Wei,Cheng Ming.Cogging torque reduction of flux-switching permanent magnet machines without skewing[C]//International Conference on Electrical Machines and Systems,Wuhan,2008:3020-3025.
[5] Jin M J,Wang Y,Shen J X,et al.Cogging torque suppression in a permanent magnet flux-switching integrated-starter-generator[J].IET Electric Power Applications,2010,4(8):647-656.
[6] Zhao Jing,Yan Yashuang,Li Bin,et al.Influence of different rotor teeth shapes on the performance of flux switching permanent magnet machines used for electric vehicles[J].Energies,2014,12(7):8056-8075.
[7] Fei Weizhong,Luk P C K,Shen Jianxin.Torque analysis of permanent-magnet flux switching machines with rotor step skewing[J].IEEE Transactions on Magnetics,2012,48(10):2664-2673.
[8] 刘承军,张辉,邹继斌.永磁同步电机齿槽定位力矩补偿[J].电工技术学报,2007,22(7):131-135.
Liu Chengjun,Zhang Hui,Zou Jibin.Compensation for the cogging torque of permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2007,22(7):131-135.
[9] 贾红云,程明,花为,等.基于电流谐波注入的磁通切换永磁电机定位力矩补偿方法[J].中国电机工程学报,2009,29(27):83-89.
Jia Hongyun,Cheng Ming,Hua Wei,et al.Cogging torque compensation for flux-switching permanent magnet motor based on current harmonics injection[J].Proceedings of the CSEE,2009,29(27):83-89.
[10]王伟华,肖曦,丁有爽.永磁同步电机改进电流预测控制[J].电工技术学报,2013,28(3):50-55.
Wang Weihua,Xiao Xi,Ding Youshuang.An improved predictive current control method for permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2013,28(3):50-55.
[11]Zhang Yongchang,Yang Haitao,Xia Bo.Model predictive control of induction motor drives:flux control versus torque control[J].IEEE Transactions on Industry Applications,2016,52(5):4050-4060.
[12]张永昌,杨海涛,魏香龙.基于快速矢量选择的永磁同步电机模型预测控制[J].电工技术学报,2016,31(6):66-73.
Zhang Yongchang,Yang Haitao,Wei Xianglong.Model predictive control of permanent magnet synchronous motors based on fast vector selection[J].Transactions of China Electrotechnical Society,2016,31(6):66-73.
[13]Cheng Ming,Yu Feng,Chau K T,et al.Dynamic performance evaluation of a nine-phase flux-switching permanent-magnet motor drive with model predictive control[J].IEEE Transactions on Industrial Electronics,2016,63(7):4539-4549.
[14]魏玉香,夏长亮,刘涛,等.两电机转矩同步系统有限集模型预测控制[J].电工技术学报,2016,31(19):115-122.
Wei Yuxiang,Xia Changliang,Liu Tao,et al.Finite control set model predictive control for dual-motor torque synchronous system[J].Transactions of China Electrotechnical Society,2016,31(19):115-122.
[15]Rodriguez J,Kennel R M,Espinoza J R,et al.High-performance control strategies for electrical drives:an experimental assessment[J].IEEE Transactions on Industrial Electronics,2012,59(2):812-820.
[16]Cai Hua,Xu Wei,Yang Wenwu,et al.New model based predictive torque control algorithm in combination with duty ratio modulation strategy for flux-switching permanent magnet synchronous machines[C]//International Conference on Electrical Machines and Systems,Busan,2013:1160-1165.
[17]Fan Ying,Zhang Li,Cheng Ming,et al.Sensorless SVPWM-FADTC of a new flux-modulated permanent-magnet wheel motor based on a wide-speed sliding mode observer[J].IEEE Transactions on Industrial Electronics,2015,62(5):3143-3151.
(编辑 于玲玲)
A Model Predictive Torque Control Scheme for Flux-Switching Permanent Magnet Machines with Cogging Torque Compensation
HuangWentao1HuaWei1YuFeng2
(1.School of Electrical Engineering Southeast University Nanjing 210096 China 2.School of Electrical Engineering Nantong University Nantong 226019 China)
To alleviate the influence of the cogging torque,this paper develops a model predictive torque control (MPTC) scheme with cogging torque compensation for flux-switching permanent magnet (FSPM) machines.Firstly,the mathematical expression of the main harmonic components of cogging torque is obtained by finite element analysis.Then,according to the compensating control theory,a cogging-torque-compensating model is constructed to counteract the cogging torque.Further,based on the MPTC method,the cogging-torque-compensating model,the predictive torque model and the predictive flux model are employed to design the cost function.Both simulations and experiments verify that the developed control scheme not only compensates the cogging torque and suppresses the torque ripple,but also offers good dynamic performances.It should be emphasized that it is also applicable to conventional permanent magnet synchronous machines.
Flux-switching permanent magnet machine,cogging torque compensation,model predictive torque control (MPTC),torque ripple
江苏省科技支撑计划(工业部分)资助项目(BE2014114)。
2016-08-20 改稿日期2017-01-19
10.19595/j.cnki.1000-6753.tces.L70654
TM351
黄文涛 男,1989年生,博士研究生,研究方向为永磁同步电机预测控制。
E-mail:hwt109@126.com(通信作者)
花 为 男,1978年生,教授,博士生导师,研究方向为新型永磁电机本体分析设计与控制等。
E-mail:huawei1978@seu.edu.cn
