T型直线超声波电动机的运行机理及其特性分析

王光庆 徐文潭 杨斌强

(浙江工商大学信息与电子工程学院 杭州 310018)

T型直线超声波电动机的运行机理及其特性分析

王光庆 徐文潭 杨斌强

(浙江工商大学信息与电子工程学院 杭州 310018)

提出了一种新型T型直线超声波电动机，利用PZT d31模式激发压电双晶悬臂梁产生纵向振动，并通过驱动足与滑条间的摩擦作用带动滑条作直线运动。研究了电动机结构和运行机理，采用有限元方法对T型直线超声波电动机定子进行了建模和分析；利用冲量定理和力平衡原理建立电动机定子和滑条接触面力传递模型，仿真分析了不同预压力作用下电动机的速度-推力输出特性，实验验证了仿真分析结构的正确性。实验结果表明，在激励电压幅值Vpp为200 V和激励频率为23.75 kHz作用下，电动机在预压力为50 N时的空载直线速度达到250 mm·s-1，在预压力为200 N时的最大推力达到7.6 N。

直线超声波电动机 压电双晶悬臂梁 T型结构 运行机理 d31模式 力传递模型

0 引言

超声波电动机是利用压电材料的逆压电效应激发定子弹性体产生超声频域的振动，并通过摩擦接触驱动与之耦合的动子做旋转或直线运动。超声波电动机具有结构简单、低速大力矩、响应速度快、断电自锁、无噪声和不受电磁干扰等优点，广泛用于精密器械、航空航天、医疗仪器、工业自动化和机器人等高新技术领域[1,2]。

超声波电动机按运动方式可分为旋转型和直线型。直线超声波电动机具有结构设计灵活、体积小、运动精度高和良好的控制特性，在微机电系统中具有广泛的应用前景[3]。陈强等[4]研究了一种利用两组正交双压电晶片激发振动双足型直线超声波电动机的运行机理，建立了电动机的有限元模型，分析了电动机振动特性，并利用LabView阻抗方法测量了电动机定子的输入阻抗。万志坚等[5]研究了一种利用8片PZT8压电陶瓷和一块磷青铜材料矩形板粘接而成的面内弯纵型直线超声电动机，分析了直线超声电动机定子质点的切向和法向运动。王剑等[6]利用定子的一阶扭振和一阶纵振模态研制了旋转-直线型两自由度超声波电动机。W.H.Lee等[7]研制了一种碟型直线超声波电动机用于超薄电子产品中。Shi Yunlai等[8]和Wan Zhijian等[9]利用纵振动和弯曲振动研制了一种基于面内模态的直线超声波电动机。Yang Xiaohui等[10]利用压电陶瓷的弯曲振动研制了纵弯复合型直线超声波电动机，电动机在峰峰值450 V驱动电压激励下输出最大速度为560 mm/s，最大输出力为55 N。Hou Xiaoyan等[11]利用三个压电叠堆d33模式产生的纵向振动研制了一种基于面内振动模态的小型直线超声波电动机。该电动机结构简单，易于控制，电动机定子结构尺寸为12 mm×4 mm×4 mm，每个压电叠堆由18片厚度为0.3 mm的压电陶瓷片和18片铝电极粘接而成，陶瓷片在机械上串联、电学上并联，压电叠堆制作工艺复杂，制造成本也较高。另外，电动机在运行过程中，因弯曲振动的影响，压电叠堆中陶瓷片与电极之间会受到较大的弯曲力变形，容易使陶瓷片与电极之间产生脱胶断裂现象。

本文采用三个压电双晶悬臂梁结构代替三个压电叠堆，研制了一种利用PZT d31模式工作的T型直线超声波电动机。每个压电双晶悬臂梁由两片极化方向相反、工作模式为d31的陶瓷片粘接在金属悬臂梁基板上、下表面构成。当两压电陶瓷在极化方向(3轴)受激励电压作用时，同时在1轴方向产生相反的扩张或收缩变形，在两个反向变形的作用下，悬臂梁的弯曲振动被抑制，只存在沿1轴方向上的伸长或收缩变形。该电动机结构简单，制造方便，成本低廉。

1 T型电动机结构及运行机理

1.1 电动机总体结构

本文所研制的T型直线超声波电动机结构如图1所示，主要由定子、滑条、底座、导轮、预压力调节螺栓和弹簧组成。定子由固定框、三个压电双晶复合悬臂梁和一个带有驱动足的中心质量块构成。定子通过五个螺钉安装固定在底座上，预压力调节螺栓和弹簧产生的压紧力使滑条与定子驱动足接触。为了保持滑条的平稳性，滑条的前、后两端通过压紧力支撑在底座的两个导轮上，导轮对滑条起导向和支撑作用。为了保证三个压电悬臂梁与固定框的连接处是固定边界条件，要求固定框的刚度远大于压电悬臂梁的刚度，这样固定框的变形远小于悬臂梁的变形，其对悬臂梁振动特性的影响可以忽略。三个压电双晶复合悬臂梁一端与中心质量块相连，另一端固定在定子固定框上，它们在结构上组成一个T型。每个压电双晶复合悬臂梁是由两片极化方向相反的压电陶瓷片(沿厚度方向极化)通过粘合剂粘接在金属弹性板的上、下表面构成，如图2所示。

图1 T型直线超声波电动机结构原理示意图Fig.1 Schematic of the T-shaped linear ultrasonic motor structure

图2 定子结构简图Fig.2 Schematic of the motor stator

1.2 运行机理

当相位差为180°的正弦激励电压分别沿x轴方向(极化方向)施加在左、右压电双晶悬臂梁压电陶瓷上时，电动机模态I被激发。左侧悬臂梁表面两压电陶瓷因z轴方向施加的电场(如图3a所示)作用，PZT1和PZT2在z轴方向上同时产生大小相等、方向相反的弯曲扩张运动B1和B2，且B1=-B2，在B1和B2的合成作用下，压电悬臂梁沿3轴方向上的弯曲振动被抑制，仅存在沿x轴方向的伸长变形，如图3b所示。同理，右侧悬臂梁表面两压电陶瓷在电场(如图3c所示)作用下，PZT3和PZT4在z轴方向上同时产生大小相等、方向相反的弯曲收缩运动B3和B4，且B3=-B4，在B3和B4的合成作用下，悬臂梁的弯曲振动被抑制，仅存在沿x轴方向的收缩变形，如图3d所示。左侧悬臂梁的伸长变形和右侧悬臂梁的收缩变形将使质量块和驱动足沿x方向做水平右向移动；在左、右两悬臂梁产生伸长和收缩变形作用下，下侧压电双晶复合悬臂梁将向右产生弯曲振动。反之，质量块和驱动足做水平左向移动。对于下侧压电双晶复合悬臂梁而言，压电陶瓷的极化方向沿z轴(即陶瓷的3轴方向)，形变方向沿y轴，此即压电陶瓷的y轴方向，当正弦激励电压施加在下侧压电双晶悬臂梁的两压电陶瓷上时，电动机模态II被激发，PZT5和PZT6在z轴方向上同时产生大小相等、方向相反的扩张(或收缩)运动B5和B6，且B5=-B6，在B5和B6的合成作用下，悬臂梁的弯曲振动被抑制，仅存在沿y轴方向的伸长(或收缩)变形，导致质量块和驱动足沿y轴方向做向上或向下移动。此时，左、右两侧压电悬臂梁则产生向上或向下的弯曲振动。当电动机模态I和模态II同时被激发时，驱动足表面质点将在xOy平面内产生椭圆运动轨迹，驱动与之接触的滑块做直线运动。

图3 压电双晶复合梁d31振动模式Fig.3 d31 modes of the bimorph cantilever beam

假设驱动足在模态I被激发状态下产生沿x方向的振动为[12，13]

ux(t)=u1sin(ω1t+φ1)

(1)

式中，u1、ω1和φ1分别为模态I被激发时驱动足的振动幅值、频率和初始相位角。

驱动足在模态II被激发状态下产生沿y方向的振动为

uy(t)=u2sin(ω2t+φ2)

(2)

式中，u2、ω2和φ2分别为模态II被激发时驱动足的振动幅值、频率和初始相位角。

当模态I和模态II的频率和激励频率一致时，即ω=ω1=ω2，则驱动足的运动轨迹可由式(1)和式(2)复合而成，当φ1-φ2=90°，则有

(3)

式(3)反映了驱动足的运动轨迹是一个椭圆。

2 T型电动机定子有限元模型

利用有限元方法对电动机定子的特性和结构进行优化分析。图4为电动机定子结构有限元模型，其中质量块、驱动足以及压电双晶悬臂梁的金属弹性体选用3D八节点线性结构SOLID45单元建模，压电陶瓷片选用3D八节点六面体耦合场SOLID5单元建模。压电陶瓷表面电极采用SHELL63薄膜单元建模。由于压电陶瓷与金属弹性体之间的粘合剂的厚度很小，建模分析中忽略了它们的影响。

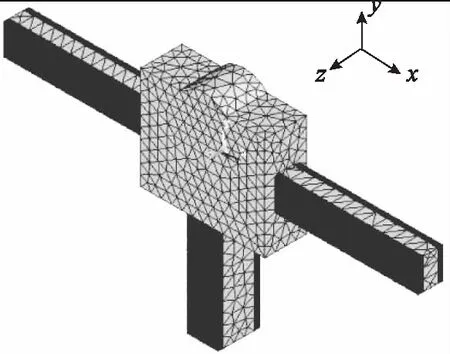
图4 电动机定子有限元模型Fig.4 FEM model of the motor stator

图2中“+”、“-”符号表示压电陶瓷片的极化方向，在有限元模型中压电陶瓷的极化方向是由压电材料PZT压电常数矩阵中d31、d33和d15符号决定的。因图2中PZT1和PZT2、PZT3和PZT4、PZT5和PZT6的极化方向相反，故它们的压电常数d31、d33和d15的符号相反。建模中，将PZT1和PZT2压电电极进行节点自由度耦合，耦合点设置为电压自由度，其中，PZT1和PZT2外表面电极的节点电压自由度耦合为通用节点“1”和“2”，PZT1、PZT2与金属基板相粘接的两个压电电极耦合成一个参考点，其参考电动势设为0；PZT3和PZT4外表面电极的节点电压自由度耦合为通用节点“3”和“4”，PZT3、PZT4与金属基板相粘接的两个压电电极耦合成一个参考点，其参考电势设为0。另外，PZT1和PZT3的极化方向也是相反的。图2中下侧压电双晶悬臂梁中PZT5和PZT6的极化方法是相反的，因此PZT5的压电常数d31、d33和d15与PZT6的压电常数d31、d33和d15的符号相同。将下侧压电电极的各个面进行节点耦合，耦合点设置电压自由度。PZT5和PZT6外层压电片两侧电极的节点电压自由度耦合为通用节点“5”和“6”，PZT5、PZT6与金属基板相粘接的两个压电电极耦合成一个参考点，其参考电动势设为0。为了模拟压电悬臂梁与固定框之间的固支边界连接条件，有限元模型中在三个压电悬臂梁与固定框相连的一端施加了x、y、z三个方向的位移约束。

电动机定子模型中，质量块的结构尺寸为12 mm×10 mm×4 mm，左、右压电双晶悬臂梁的结构尺寸为20 mm×3 mm×2.4 mm，下压电双晶悬臂梁的结构尺寸为3 mm×15.1 mm×3 mm。电动机定子结构材料参数见表1。

表1 电动机定子材料参数Tab.1 Material parameters of the motor stator

2.1 模态分析

经有限元仿真分析得到的电动机定子工作模态如图5所示，其中模态I是左侧压电双晶悬臂梁沿水平方向伸长变形，右侧压电双晶悬臂梁沿水平方向收缩变形，下压电双晶悬臂梁在左、右两压电双晶悬臂梁的变形作用下向右弯曲变形，质量块和驱动足向右移动，模态I的振动频率为22 642 Hz。模态II是下侧压电双晶悬臂梁产生向上的伸长变形，左、右侧压电双晶悬臂梁在下压电双晶悬臂梁的变形作用下产生向上弯曲振动，质量块和驱动足向上移动，模态II的振动频率为22 689 Hz。模态I与模态II振动频率基本保持一致，相对误差为0.21%。图5结果还表明：定子模态I和模态II的振动主要发生在xOy平面内，这正是本文设计所期待的工作平面。

图5 电动机定子工作模态Fig.5 Working Modals of the motor stator

2.2 谐响应分析

为了获取电动机定子的动态特性，对电动机定子的谐响应特性进行了有限元计算和分析。为了激发电动机定子模态I和II，给左、右压电双晶悬臂梁的两片压电陶瓷施加相位差为180°的正弦激励电压V1和V2，给下压电双晶悬臂梁的两片压电陶瓷施加与V1相位差为90°的激励电压V3，如式(4)～式(6)所示。

V1=100sin(ωt)

(4)

V2=100sin(ωt+π)

(5)

(6)

式中，ω=2πf，f为激励电压频率，其变化范围设定为[20,25]kHz。电动机定子结构阻尼系数设置为0.01。

经有限元计算得到电动机定子驱动足的位移幅值响应和相位响应曲线如图6所示。从图6a中可以看出，驱动足水平方向(沿x方向)的振动位移幅值和垂直方向(沿y方向)的振动位移幅值分别在激励频率22 625 Hz和22 675 Hz时达到最大，且两者远大于沿z轴方向的振动位移，这说明电动机定子的振动位移主要发生在xOy平面内，与模态分析结果一致。此外，定子驱动足水平方向和垂直方向的振动特性具有相近的相位响应特性，如图6b所示。

图6 定子谐响应分析结果Fig.6 Resonant response of the motor stator

若单独激发电动机定子模态I，即给左、右压电双晶悬臂梁的两片压电陶瓷施加正弦激励电压V1和V2，下压电双晶悬臂梁的两片压电陶瓷施加正弦激励电压为0V，计算得到驱动足x方向的振动位移在频率22 625 Hz时达到最大。同理，若单独激发电动机模态II，即给左、右压电双晶悬臂梁的两片压电陶瓷施加正弦激励电压0 V，下压电双晶悬臂梁的两片压电陶瓷施加正弦激励电压为V3，计算得到驱动足y方向的振动位移在频率22 675 Hz时达到最大，这与图6所示的结果比较一致。分析结果表明定子x和y方向振动位移的大小主要取决于各自方向上所施加激励电压的幅值和频率，而彼此之间影响较小。这说明定子x和y方向的振动位移具有很好的解耦性，这有利于电动机结构的优化和驱动控制电路的设计。另外，从图5和图6的谐响应分析结果还可以看出在模态I和模态II分别被激励时，定子的振动频率分别为22 625 Hz和22 675 Hz，与模态分析计算得到的振动频率是一致的。谐响应和模态分析两者频率误差主要是由于前者考虑了耦合电压的影响，而后者未考虑耦合电压的影响。

2.3 瞬态分析

将式(4)～式(6)正弦电压分别加载到左、右和下压电双晶悬臂梁的两片压电陶瓷上，激励电压频率为22 625 Hz，每个周期分成10个加载子步，定子结构阻尼为1%。通过有限元计算得到驱动足x和y方向的振动位移时间历程曲线如图7所示。由图7可知，电动机定子经过2 ms后进入稳定振动状态，表明具有较快的位移响应速度，可以用在一些响应速度要求较快的场合，如微型机器人的驱动与控制。稳态后，电动机定子在x和y方向的振动位移幅值分别达到1.9 μm和1.4 μm，振动速度分别达到270 mm·s-1和200 mm·s-1。

图7 定子驱动足的振动位移Fig.7 Vibration displacements of the stator teeth

从图7中提取电动机定子x和y方向的振动位移可以得到稳态时定子椭圆运动轨迹，如图8所示。从图8可以看出驱动足质点的运动轨迹是一个倾斜的椭圆，这对电动机的机械输出特性会有一定的影响，可以通过调整驱动电压V1和V3的相位差来补偿。

图8 定子椭圆运动轨迹Fig.8 Elliptical orbit of the stator

另外，由于定子结构具有良好的对称性，电动机正、反向运行特性具有较好的一致性，只要V1和V2对调分别施加在左、右压电双晶悬臂梁上，即可实现电动机的反向运行。此时，定子驱动足质点的椭圆轨迹与正向运行时的椭圆轨迹关于x=0对称，如图8所示。

3 电动机机械特性分析

根据瞬态分析得到的电动机定子驱动足振动位移结果，以滑条为研究对象，在y方向利用冲量守恒定理，在x方向利用力平衡原理，则有[13-17]

(7)

(8)

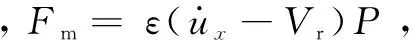
表2 定子性能仿真参数
Tab.2 Simulation parameters of the stator

根据文献[14，15]，积分式(7)和式(8)可得电动机一个周期内的水平速度Vr和平均输出推力FT为

(9)

(10)

式中，PT为临界预压力，PT=kfUy，其中Uy为y方向振动位移uy的幅值；Vmax为定子驱动足质点水平方向振动最大速度；φ为接触角。表2是用于仿真计算的电动机定子结构参数[12]。

图9为电动机定子与滑条间预压力与接触角之间的关系曲线，可以看出，随着定子与滑条间预压力的增加，接触角也逐渐增大。当预压力增加到临界点260N时，接触角φ=2π，表明定子与滑条表面整个振动周期都接触。此后，总预压力继续增加，接触角则保持不变。

图9 接触角与预压力关系曲线Fig.9 Relationship between the contact angle and preload

图10为不同预压力作用下，电动机空载速度和推力之间关系的仿真结果。从图10可以看出，电动机推力与空载速度呈线性递减关系，预压力增大，接触面越大，输出推力也增大，但输出速度却减小。当预压力增大到大于200N时，电动机由断续接触状态变为连续接触状态，此时，电动机输出推力达到最大值8N。继续增大预压力，电动机输出推力基本保持恒定，但输出速度急剧下降，这表明电动机定子受到的预压力过大，电动机处于过压状态。当电动机预压力较小时(P0≤10N)，电动机空载速度达到最大值268mm·s-1，这与有限元瞬态分析结果270mm·s-1比较吻合。

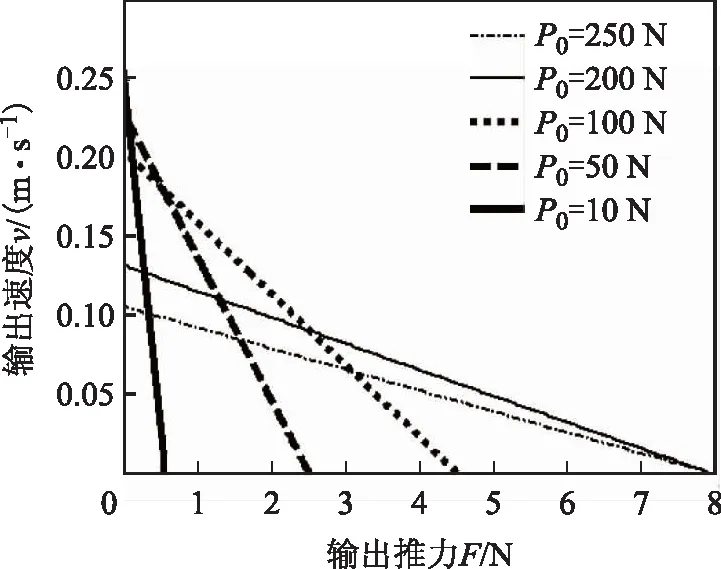
图10 不同预压力下推力与速度关系Fig.10 Thrust-speed curves of the motor

4 样机与实验结果

按照优化设计尺寸加工制作的直线电动机样机及T型定子如图11所示，T型定子采用一体化线切割机械加工而成，这样可以保证悬臂梁与框架之间固定连接。

图11 直线电动机样机及T型定子Fig.11 Prototype motor and the T-shaped stator

图12为利用阻抗分析仪(型号为PA70)对样机定子阻抗测试的结果。由图12可以看出，当水平压电双晶悬臂梁(x方向)被激励时，电动机定子谐振频率为23.74 kHz。当垂直压电双晶悬臂梁(y方向)被激励时，定子谐振频率为23.78 kHz。实验测试结果与模态I、II的计算结果相比较，两者之间存在约1.1 kHz的误差，误差产生的主要原因有：①T型定子悬臂梁结构和压电陶瓷片尺寸存在加工误差；②悬臂梁固定框使得定子整体刚度增大，导致谐振频率偏大。因此，为了减少谐振频率实验结果的误差，在确保T型定子悬臂梁和压电陶瓷尺寸精度的前提下，应尽量增大固定框架的质量，降低其对定子谐振频率的影响。

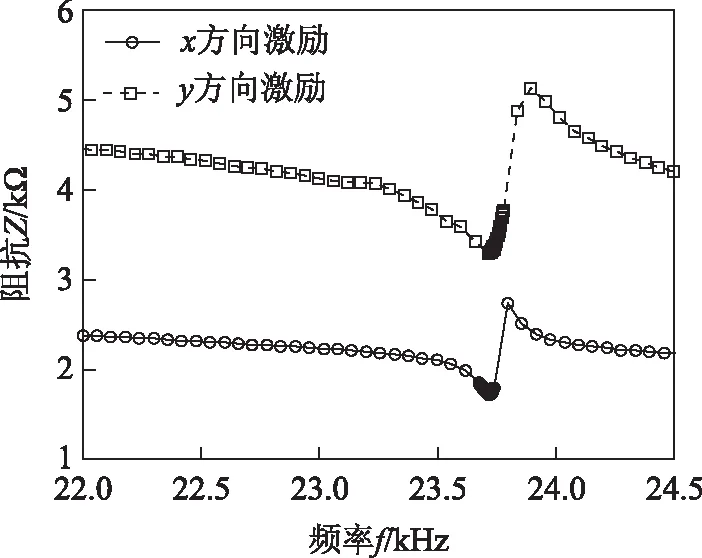
图12 样机阻抗测试结果Fig.12 Impedance results of the motor

图13为直线电动机不同预压力作用下的速度-推力特性实验结果，电动机激励电压幅值Vpp为200 V，激励频率为23.75 kHz。在预压力为50 N时，电动机空载直线速度达到250 mm·s-1，推力达到2.6 N；随着预压力的增大，电动机输出推力增大，空载直线速度下降，在预压力为200 N时，空载直线速度为130 mm·s-1，最大推力为7.6 N。与图10仿真分析结果比较可以看出，实验结果与仿真结果比较接近，说明本文直线电动机设计方法是正确可行的。

图13 电动机速度-推力特性实验结果Fig.13 Experimental results of Speed-thrust characteristics

5 结论

利用压电双晶悬臂梁的纵振动模式研制了一种T型直线超声波电动机，通过对电动机有限元、仿真和实验分析，得到以下结论：

1) 所设计的直线超声波电动机结构简单，可以避免压电叠堆因弯曲振动产生的脱胶断裂现象。

2) 仿真结果表明T型直线超声波电动机在激励电压幅值Vp为100 V和激励频率为22 625 Hz作用下，电动机空载直线速度达到270 mm·s-1，最大推力达到8 N。

3) 有限元分析结果表明所设计的直线超声波电动机x和y方向的振动位移具有良好的解耦性，有利于驱动控制电路的设计。

4) 实验结果表明在激励电压幅值Vpp为200 V和激励频率为23.75 kHz作用下，预压力为200 N时，电动机空载直线速度为130 mm·s-1，最大推力为7.6 N，实验结果与仿真结果比较接近，证明本文预测模型是正确可行的。

下一步研究工作重点：①继续优化设计T型定子结构，解决悬臂梁与固定框之间连接方式、固定框刚度效应等对定子谐振频率、振动特性的影响；②深入开展直线超声波电动机的理论模型与数值分析研究；③完善直线超声波电动机的实验研究，包括电动机阻抗特性、频率响应特性、机械输出特性(如效率-推力特性)等。

[1] Sashida T，Kenjo T.An introduction to ultrasonic motors[M].NewYork：Oxford University Press，USA，1993.

[2] Zhao C S.Ultrasonic motors technologies and applications[M].Beijing：Science Press，2011.

[3] Henderson D A.Simple ceramic motor inspiring smaller producers[J].Stroke，2006，50(10)：14-16.

[4] 陈强，徐志科，蒋春容，等.双足驱动双压电晶片直线超声波电动机运行机理研究[J].振动与冲击，2014，33(22)：21-25.

Chen Qiang，Xu Zhike，Jiang Chunrong，et al.Operation mechanism of linear ultrasonic motor installed with bimorphs and double-driving feet[J].Journal of Vibration and Shock，2014，33(22)：21-25.

[5] 万志坚，胡泓.面内弯纵型直线超声电动机的驱动与摩擦分析[J].振动、测试与诊断，2014，34(2)：229-236.

Wan Zhijian，Hu Hong.Analysis on friction driving of linear ultrasonic motor with In-plane bending and longitudinal mode[J].Journal of Vibration，Measurement & Diagnosis，2014，34(2)：229-236.

[6] 王剑，白洋，郭吉丰.旋转-直线型两自由度超声波电动机建模与设计[J].电工技术学报，2013，28(11)：48-53.

Wang Jian，Bai Yang，Guo Jifeng.Modeling and optimal design of the rotary-liner type two-degree-of-freedom ultrasonic motors[J].Transactions of China Electrotechical Society，2013，28(11)：48-53.

[7] Lee W H，Kang C Y，Paik D S，et al.Butterfly-shaped ultra slim piezoelectric ultrasonic linear motor[J].Sensors and Actuators A：Physical，2011，168(1)：127-130.

[8] Shi Yunlai，Zhao Chunsheng.A new standing-wave-type linear ultrasonic motor based on in-plane modes[J].Ultrasonics，2011，51(4)：397-404.

[9] Wan Zhijian，Hu Hong.Modeling and experimental analysis of the linear ultrasonic motor with in-plane bending and longitudinal mode[J].Ultrasonics，2014，54(3)：921-928.

[10]Yang Xiaohui，Liu Yingxiang，Chen Weishan，et al.Longitudinal and bending hybrid linear ultrasonic motor using bending PZT elements[J].Ceramics International，2013，39(Supplement 1)：S691-S694.

[11]Hou Xiaoyan，Pueh L H，Jin O C，et al.Design and finite element analysis of a new stack ultrasonic motor based on in-plane mode[J].Smart Materials and Structures，2012，21(11)：115002-1150011.

[12]王瑞霞，金龙，潘鹏，等.一种方底座短柱超声波电动机的设计[J].电工技术学报，2015，30(2)：134-139.

Wang Ruixia，Jin Long，Pan Peng，et al.A short cylindrical ultrasonic motor with square base[J].Transactions of China Electrotechical Society，2015，30(2)：134-139.

[13]Guo Jifeng，Gong Shujuan，Guo Haixun，et al.Force transfer model and characteristics of hybrid transducer type ultrasonic motors[J].IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2004，51(4)：387-395.

[14]蒋春容，陆旦宏，金龙.中空环形行波型超声波电动机定子振动机械模型[J].电工技术学报，2015，30(7)：112-118.

Jiang Chunrong，Lu Danhong，Jin Long.An analytical model of the stator vibration in the hollow ring type traveling wave ultrasonic motor[J].Transactions of China Electrotechnical Society，2015，30(7)：112-118.

[15]王光庆，岳玉秋，展永政.纵-弯复合旋转式超声波电动机的优化设计与性能分析[J].电工技术学报，2015，30(22)：33-41.

Wang Guangqing，Yue Yuqiu，Zhan Yongzheng.Optimum design and performances analysis of the longitudinal-bending hydrid rotating type ultrasonic motor[J].Transactions of China Electrotechnical Society，2015，30(22)：33-41.

[16]王光庆，陆国丽，郭吉丰.基于能量等效的行波型超声波电动机解析模型[J].机械工程学报，2008，44(2)：74-81.

Wang Guangqing，Lu Guoli，Guo Jifeng.Analytical model of traveling wave type ultrasonic motor based on the energy equivalent method[J].Chinese Journal of Mechanical Engineering，2008，44(2)：74-81.

[17]曲建俊，李锦棒.基于电接触法的行波超声电动机接触特性研究[J].声学学报，2015，40(5)：625-630.

Qu Jianjun，Li Jinbang.Contact characteristics of a traveling wave ultrasonic motor based on an electric contact method[J].Acta Acustica，2015，40(5)：625-630.

(编辑 于玲玲)

Operating Mechanism and Characteristics Analysis of a T-Shaped Linear Ultrasonic Motor

WangGuangqingXuWentanYangBinqiang

(School of Information and Electronic Engineering Zhejiang Gongshang University Hangzhou 310018 China)

A novel T-shaped linear ultrasonic motor was proposed.The d31mode of the PZT was used to excite the bimorph cantilever beams to generate a longitudinal vibration，which can push the slider to move in a straight line with the friction force between the driving feet and the slider.The general structure and operating principle of the new motor were introduced at first.Then the stator of the T-shaped linear ultrasonic motor was modeled with the finite element method (FEM)，and the force transferring model of the contact surface between the stator and the slider was established based on the impulse theorem and the force equilibrium law.With this model，simulations on the speed-thrust characteristics under different pre-load were performed，and the validity of the model was testified by the experimental results.Experimental results show that when the motor is excited by a voltage with peak-peak amplitude of 200 V and frequency of 23.75 kHz，the no-load speed of the motor reaches 250 mm·s-1when the pre-load is 50 N，and the maximum thrust reaches 7.6 N when the pre-load is 200 N.

Linear ultrasonic motor，bimorph cantilever beams，T-shaped structure，operating mechanism，d31mode，force transferring model

国家自然科学基金(51277165)、浙江省自然科学基金(LY15F010001)和浙江省教育厅(Y201223050)资助项目。

2016-04-22 改稿日期2017-01-15

10.19595/j.cnki.1000-6753.tces.160544

TM356

王光庆 男，1975年生，博士，教授，研究方向为超声波电动机及压电振动能量采集技术。

E-mail：kele76@163.com(通信作者)

徐文潭 男，1992年生，硕士研究生，研究方向为超声波电动机。

E-mail：1135987261@qq.com