阻抗不匹配引起的逆变器-IPMSM系统直流侧振荡抑制方法对比
2017-08-31方晓春钟志宏杨中平
方晓春 钟志宏 杨中平 林 飞
(北京交通大学电气工程学院 北京 100044)
阻抗不匹配引起的逆变器-IPMSM系统直流侧振荡抑制方法对比
方晓春 钟志宏 杨中平 林 飞
(北京交通大学电气工程学院 北京 100044)
随着逆变器-内置式永磁同步电机(IPMSM)系统输出功率的增加,其输入阻抗与直流供电端LC滤波环节输出阻抗不再匹配,引发逆变器直流侧电压、电流振荡。针对IPMSM,推导了逆变器-电机系统采样双电流调节器控制时的输入导纳模型,用于系统稳定性分析。参考异步电机系统振荡抑制方法,根据IPMSM转矩公式,提出直轴电流补偿法和直轴电压补偿法两种振荡抑制办法。结合交轴电流补偿法、交轴电压补偿法思想,推导了分别加入四种振荡抑制方法后的逆变器-IPMSM系统输入阻抗,采用奈奎斯特判据,分析各振荡抑制方法的有效性。依据电机模型与控制系统模型,分析不同方法的优劣,提出电压补偿法优于电流补偿法、交轴补偿法优于直轴补偿法的观点。通过实验验证了各振荡抑制方法的有效性和交轴电压补偿法的优势。
内置式永磁同步电机 阻抗匹配 直流侧振荡 阻尼补偿 振荡抑制
0 引言
直流供电逆变器-电机传动系统在电机高性能闭环控制下,随着系统输出功率的增加,会出现逆变器直流侧电压、电流振荡的不稳定现象[1,2]。该不稳定现象是由于LC滤波环节输出阻抗与逆变器-电机系统输入阻抗的不匹配造成的。该类阻抗不匹配失稳现象可以通过改变LC滤波环节输出阻抗和逆变器-电机系统输入阻抗两个方面进行抑制。两者分别被称为被动与主动阻尼补偿策略。被动阻尼补偿策略通过改变硬件电路参数实现阻抗匹配,在实际应用中受诸多条件限制[3,4]。主动阻尼策略在电机控制指令中注入补偿信号进行振荡抑制,是解决该类不稳定现象的可靠方案[5,6]。
永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)具有功率密度高、效率高、可进行全封闭设计减小维护量等优点[7,8],在轨道交通等工业领域被广泛关注。永磁同步电机有表面式和内置式两种转子结构,其中内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor,IPMSM)的永磁体位于电机转子内部,电机机械强度高,磁路气隙小,功率密度大,尤其适合轨道交通应用。当PMSM被应用于城轨列车等直流供电传动系统时,需对阻抗不匹配引起的直流侧振荡进行抑制。
逆变器-电机系统输入阻抗模型和补偿信号的注入点选择是主动阻尼补偿策略两个关键研究点。逆变器-电机系统输入阻抗模型可分为理想恒功率源模型和控制系统频域导纳模型。根据理想模型进行系统参数设计和阻尼补偿,很可能得到过保险的系统阻尼解决方案[9]。建立逆变器-电机控制系统线性化模型,进行频域特性分析是当前的主流分析方法[10,11]。现有文献为简化逆变器-电机系统的输入阻抗表达式,电机往往采用表贴式永磁同步电机,其交、直轴电感相等,电机状态方程简单;电机控制采用id=0控制,进一步简化输入阻抗解析式。
针对逆变器-PMSM系统,现有文献中的主动阻尼补偿策略通常把阻尼补偿信号注入点选择在电机交轴控制量上,即往往采用交轴电流补偿法与交轴电压补偿法进行振荡抑制。文献[12]基于异步电机系统,对在交轴与直轴电压上注入补偿信号的效果进行了比较,并得到在直轴电压上进行补偿效果更好的结论。IPMSM控制过程中,交、直轴电气量相互耦合,且直轴电流直接影响输出转矩的磁阻转矩部分,在交轴或直轴控制量上进行振荡补偿都有理论依据。但尚无文献针对PMSM直轴电流或电压补偿法进行研究,更缺乏不同主动阻尼补偿法振荡抑制效果之间的对比研究。
本文针对IPMSM,建立双电流环控制下的输入导纳模型,用于分析系统稳定性和设计振荡抑制方法。参考异步电机系统直轴补偿法,结合IPMSM模型,提出用于IPMSM系统的直轴电流补偿法与直轴电压补偿法,并与现有的交轴电流补偿法和交轴电压补偿法进行对比研究。针对加入阻尼补偿后的系统导纳模型进行推导,采用奈奎斯特定理,对振荡效果进行验证。根据电机模型与控制系统模型,对不同振荡抑制方法的优劣进行分析,得出双电流调节器控制下逆变器-IPMSM系统的较优振荡抑制方法。通过实验,对所提观点进行了论证。
1 振荡机理与系统模型
1.1 振荡机理
图1为直流供电逆变器-电机传动系统拓扑简图。假设控制器带宽无限大,逆变器为连续能量转换系统,PMSM输出转矩或转速能完美跟随指令值,逆变器-PMSM系统可视为理想恒功率负载而呈现负阻抗(导纳)特性。该模型下,系统稳定的基本条件是系统阻尼系数为正,系统稳定判据为
(1)
式中,P0、uc0分别为稳态输出功率与直流电压;R、L、C分别为直流侧电阻、电感、电容。式(1)是该类不稳定现象的经典通用判据。根据理想模型判据,系统随着输出功率的上升逐渐失稳;逆变器直流侧参数的取值与逆变器-电机系统呈现的负阻抗特性是该类不稳定现象的根本原因。
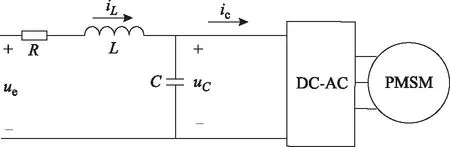
图1 传动系统结构简图Fig.1 The structure diagram of drive system
为进行更加合理的振荡抑制控制器设计和系统性能分析,求解系统综合线性化模型,进行频域特性分析是很有必要的。对此类传动系统稳定性进行频域特性分析,可以引用直流分布式电源系统的一般性结论。文献[13]提出,对于如图2所示的典型直流分布式电源系统,即使各子模块单独设计满足稳定性要求,集成的大系统由于各子系统间的交互关系,也可能会出现系统性能下降,甚至出现不稳定现象,导致中间直流母线电压、电流振荡。其根本原因是电源侧输出阻抗Zout与负载侧输入阻抗Zin不匹配。解决方案为综合设计系统阻抗匹配关系,使得电源侧输出阻抗Zout与负载侧输入阻抗Zin的阻抗比Zout/Zin满足奈奎斯特稳定判据。
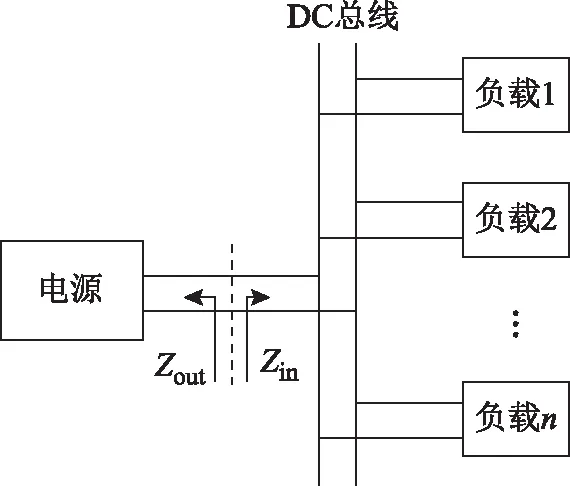
图2 典型直流分布式电源系统Fig.2 Typical DC distributed power system
直流供电逆变器-电机系统直流侧振荡是图2所示直流分布式电源系统阻抗不匹配失稳问题的一个特例。电源侧具有一个较大的滤波电感和较小的支撑电容,系统需要匹配负载侧输入阻抗Zin才能实现系统稳定性控制。Zout/Zin转换为系统导纳模式则为Yin/Yout,可视为系统环路增益。判断传动系统稳定性的闭环传递函数可表示为[14]
(2)
式中,Yin为逆变器-电机系统输入导纳;Yout为直流侧LC环节输出导纳。根据该级联电气系统开环传递函数,即导纳比Yin/Yout就可判断传动系统阻抗是否匹配,系统是否稳定。具体判据为:针对开环传递函数Yin/Yout,绘制奈奎斯特图,当ω从-∞变化到+∞时,奈奎斯特曲线不环绕点(-1,0)。
1.2 系统导纳模型
直流侧LC环节输出导纳Yout推导较为简单,且在众多文献中皆有描述,本文直接给出结果,为
(3)
逆变器-电机系统输入导纳Yin的求解需要分别针对逆变器、电机以及电机控制系统进行建模。假设逆变器无能量损耗,交流侧输出功率等于直流侧输入功率,即
(4)
式中,uC为逆变器直流侧电容电压;ic为逆变器直流侧输入电流;id、iq分别为电机d、q轴电流;ud、uq分别为d、q轴电压。考虑控制延时Td,逆变器电压模型为
(5)
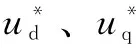
IPMSM在两相同步旋转坐标系下定子电压方程与运动方程为
(6)
(7)
式中,Ld、Lq分别为d、q轴电感;Rs为定子内阻;ψf为永磁体磁链;pn为极对数;Ωr为机械角速度;J为驱动系统旋转结构转动惯量;Tl为负载转矩;Tm为摩擦转矩。采用双电流调节器,并对交、直轴电流进行解耦控制,是PMSM在未进行弱磁控制时的典型控制框架。从而,电流调节器可表示为
(8)
式中,Gq(s)、Gd(s)分别为交、直轴电流PI控制器,Gq(s)=(kqp+kqi/s),Gd(s)=(kdp+kdi/s);pnΩrLqiq与pnΩr(ψf+Ldid)是电机的解耦项。对式(4)~式(8)依次进行线性化可得
(9)
令
(10)
将式(10)代入式(9)的第二~第五个等式,可以得到
(11)
令
(12)
将式(11)、式(12)带入式(9)的第一个等式,可得到双电流调节器控制下逆变器-IPMSM输入导纳为
(13)
2 振荡抑制策略
主动阻尼补偿的本质在于改变电机输出转矩,将直流侧振荡的电能转换成电机输出机械能,以达到抑制振荡的目的。对于电机控制系统,阻尼补偿信号注入点包括转矩(转速)指令、电流指令和电压指令。阻抗不匹配引起的直流侧振荡频率接近且小于直流侧LC谐振频率,将阻尼补偿信号加在转矩(转速)指令上受控制带宽限制而影响振荡抑制效果。因此,阻尼补偿信号往往加在电流或电压指令上。IPMSM转矩公式为
(14)
根据式(14),交、直轴电流都能够直接影响电机输出转矩。从而,即使控制过程中交、直轴完美解耦,在交轴或直轴控制量上注入阻尼补偿信号都能达到抑制振荡的目的。
2.1 交轴电流补偿法
提取直流环节电压振荡信号,经过比例控制器进行缩放,修正交轴电流指令抑制系统振荡的主动阻尼补偿策略称为交轴电流补偿法。图3为交轴电流补偿法控制框图,其中Hqc为补偿控制器,由比例控制器和带通滤波器构成,为
(15)
式中,ζ为阻尼比;ωc为滤波器中心截止频率;Kqc为交轴电流补偿法的控制系数,取正值。加入补偿后,式(9)的第五个等式变为
(16)
令
(17)
将式(10)、式(17)带入式(16)与式(9)的第二~第四个等式,得到
(18)
将式(12)、式(18)带入式(9)的第一个等式,即可得到采用交轴电流补偿法后的逆变器-IPMSM输入导纳方程为
(19)
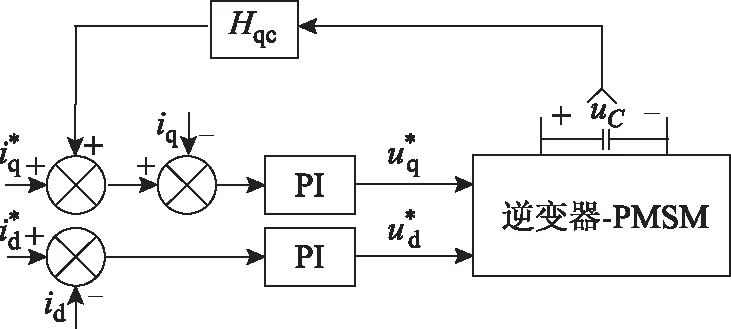
图3 交轴电流补偿法控制框图Fig.3 q-axis reference current based compensator
为验证振荡抑制方法的有效性,对比未加补偿与加入交轴电流补偿法后的Yin/Yout奈奎斯特图。本文研究基于图4所示的7.5 kW电机平台,平台关键参数见表1。

图4 7.5 kW永磁同步电机对拖实验平台Fig.4 7.5 kW PMSM experimental platform
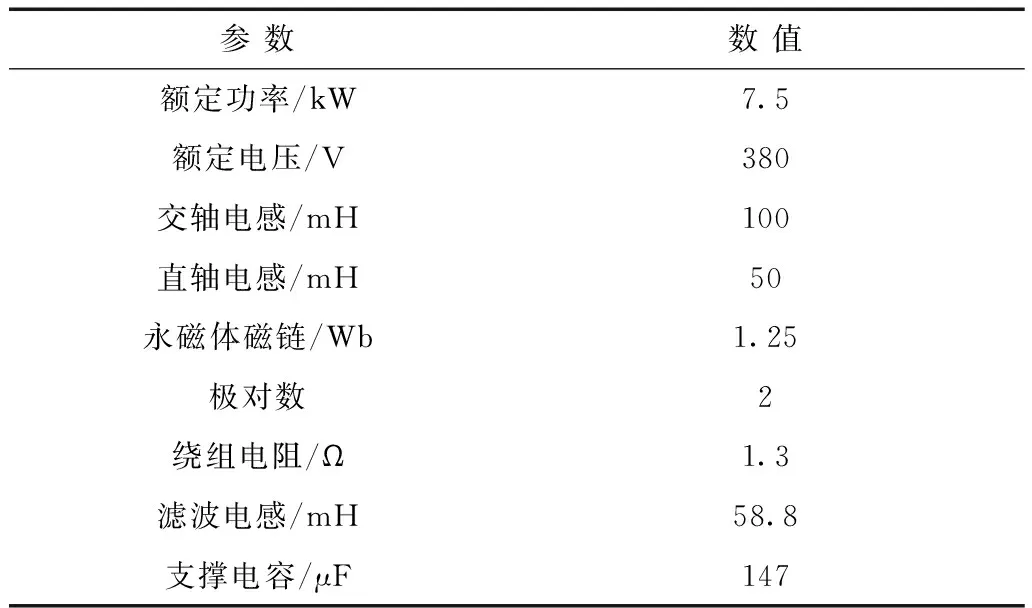
参数数值额定功率/kW7.5额定电压/V380交轴电感/mH100直轴电感/mH50永磁体磁链/Wb1.25极对数2绕组电阻/Ω1.3滤波电感/mH58.8支撑电容/μF147
设表1所示电机机械角速度为40 rad/s,交轴电流指令值为12 A,直轴电流指令值为-5 A,交、直轴电流指令满足最大转矩电流比控制。对比加入振荡抑制方法前后的Yin/Yout奈奎斯特曲线如图5所示。
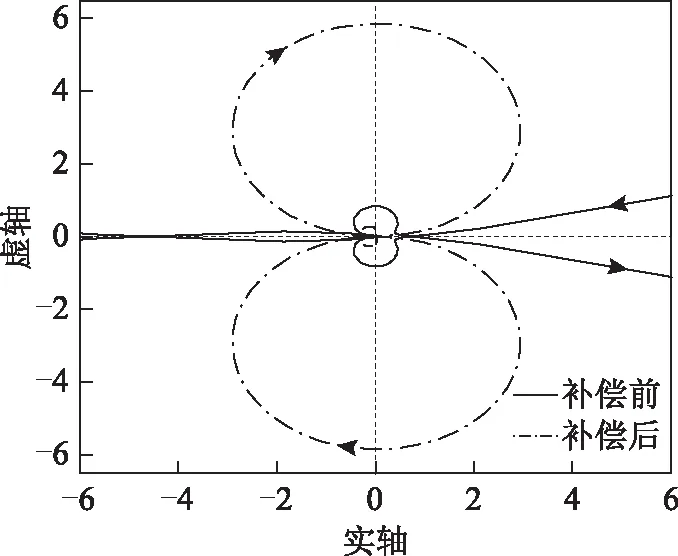
图5 采用交轴电流补偿法前后系统奈奎斯特图对比Fig.5 Nyquist diagram with and without q-axis reference current based compensator
从图5中可以明显观察到,在补偿之前,系统在(-1,0)左侧有一次穿越,系统不稳定;补偿之后,系统在(-1,0)左侧没有发生穿越。交轴电流补偿法明显抑制了振荡现象的产生。
2.2 交轴电压补偿法
提取直流环节电压振荡信号,经过比例控制器进行缩放,修正交轴电压指令抑制系统振荡的主动阻尼补偿策略称为交轴电压补偿法。与2.1节推导过程相似,可以得到加入交轴电压补偿法后的逆变器-IPMSM输入导纳方程为
(20)
其中
(21)
式(21)中比例控制器参数Kqv取正值。采用与图5相同的平台参数与电机运行状态,对比加入交轴电压补偿法前后的Yin/Yout奈奎斯特曲线如图6所示。
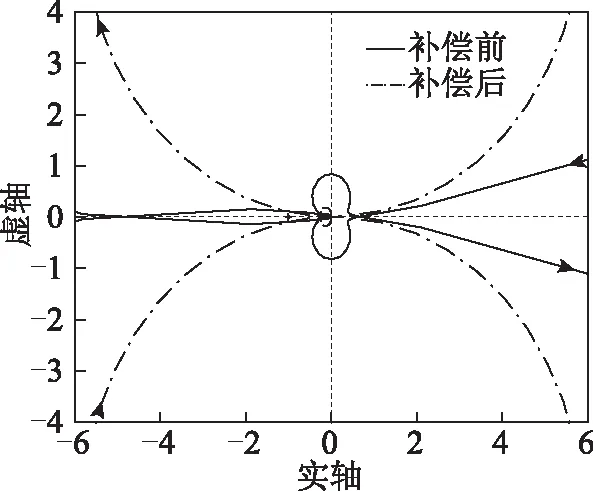
图6 采用交轴电压补偿法前后系统奈奎斯特图对比Fig.6 Nyquist diagram with and without q-axis reference voltage based compensator
由图6可知,交轴电压补偿法对振荡有明显的抑制作用。
2.3 直轴电流补偿法
提取直流环节电压振荡信号,经过比例控制器进行缩放,修正直轴电流指令抑制系统振荡的主动阻尼补偿策略称为直轴电流补偿法。与2.1节推导过程相似,可以得到加入直轴电流补偿法后的逆变器-IPMSM输入导纳方程为
[P1-D(s)P2]-1+[Gdc(s)+D(s)Z3]·
(22)
其中
(23)
式(23)中比例控制器参数Kdc取负值。采用与图5相同的平台参数与电机运行状态,对比加入直轴电流补偿法前后的Yin/Yout奈奎斯特曲线如图7所示。

图7 采用直轴电流补偿法前后系统奈奎斯特图对比Fig.7 Nyquist diagram with and without d-axis reference current based compensator
由图7可知,直轴电流补偿法对振荡也有明显的抑制作用。
2.4 直轴电压补偿法
邓翠玉等学者[27] 于2017年对24个条目的慢性病病耻感量表进行了汉化并检验了其在脑卒中患者中的信效度。总量表效度为 0.932,重测信度为0.881,证明此中文版慢性病病耻感量表的信效度良好,条目简单易懂,患者可在6min~10min完成,具有良好的适用性。慢性病病耻感量表即是以神经系统疾病为基础发展而来测量病耻感的研究工具,可以为我国神经系统疾病病耻感的测量提供统一的评估工具。
提取直流环节电压振荡信号,经过比例控制器进行缩放,修正直轴电压指令抑制系统振荡的主动阻尼补偿策略称为直轴电压补偿法。与2.1节推导过程相似,可得到加入直轴电压补偿法后的逆变器-IPMSM输入导纳方程为
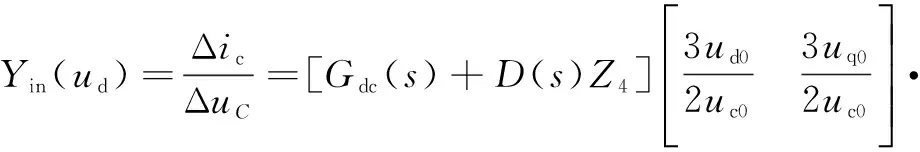
[P1-D(s)P2]-1+[Gdc(s)+D(s)Z4]·
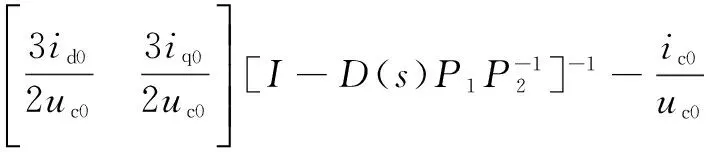
(24)
其中
(25)
式(25)中比例控制器参数Kdv取负值。采用与图5相同的平台参数与电机运行状态,对比加入直轴电压补偿法前后的Yin/Yout奈奎斯特曲线如图8所示。
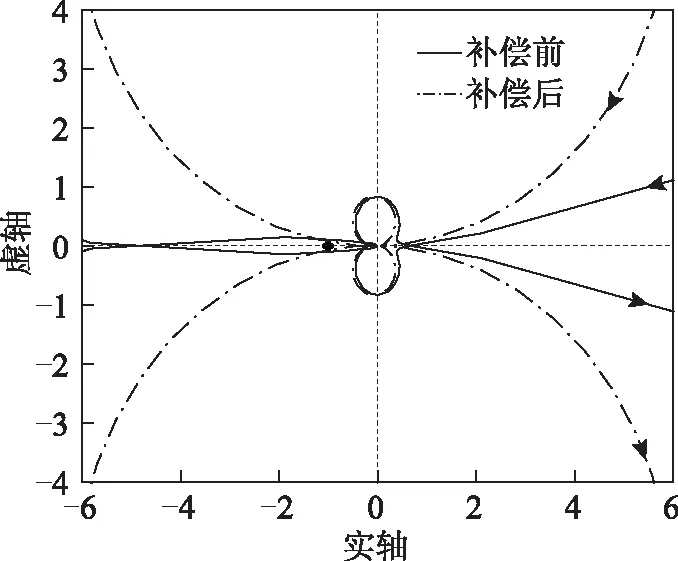
图8 采用直轴电压补偿法前后系统奈奎斯特图对比Fig.8 Nyquist diagram with and without d-axis reference voltage based compensator
由图8可知,直轴电压补偿法对振荡的抑制效果同样明显。
2.5 补偿效果对比分析
在2.1节、2.3节的理论分析中发现,电流补偿法从提取振荡信号到最终发生作用,需要经过电流调节器,得到的系统输入导纳存在一项电流调节器的传递函数。如式(17)的Z1比式(21)的Z2多了一项Gq(s),式(23)的Z3比式(25)的Z4多了一项Gd(s)。从而推论,电流补偿法较电压补偿法更易受电流环PI参数的影响,系统的鲁棒性更差。
综上所述,相较于直轴电压、电流补偿法,交轴电流补偿法、交轴电压补偿法更适合用于双电流调节器控制下逆变器-IPMSM系统阻抗不匹配振荡的抑制。
3 实验
基于图4所示实验平台,从补偿策略对谐波的抑制效果和电流环控制参数变化对补偿效果的影响两个方面对比四种补偿策略,验证交轴电压补偿法为最优主动阻尼补偿方案。
3.1 谐波抑制效果对比
图9为未加补偿以及四种补偿策略下,直流侧电压与交轴电流波形。电机转速450 r/min,交轴电流指令逐渐增加,达到8 A后保持不变。其中,图9a未加补偿策略,图9b采用交轴电流补偿法,图9c采用交轴电压补偿法,图9d采用直轴电流补偿法,图9e采用直轴电压补偿法。
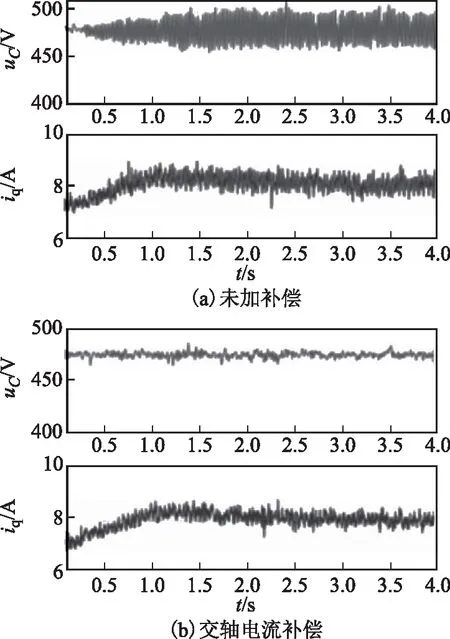
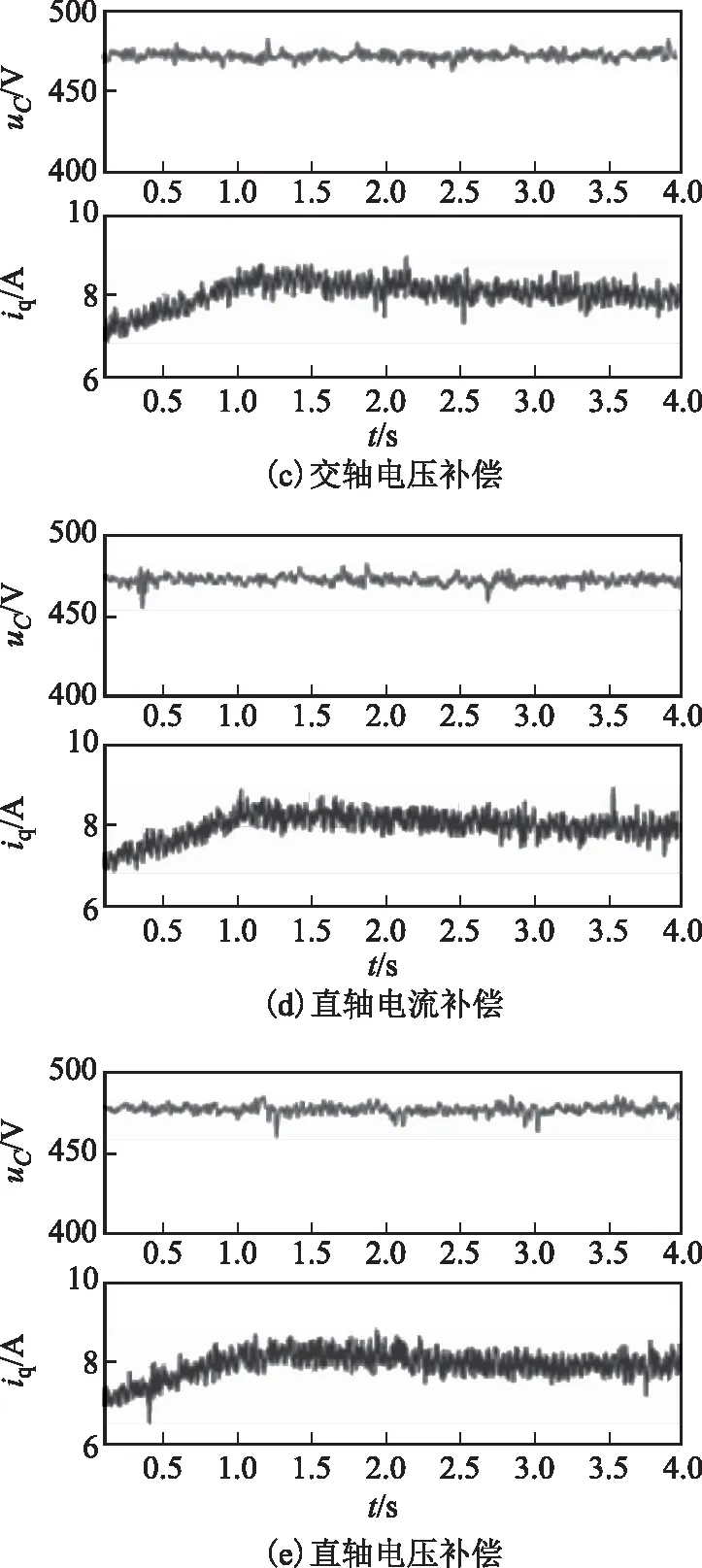
图9 不同补偿策略的振荡抑制实验对比Fig.9 Oscillation suppression with different compensators
如图9a所示,随着系统功率增加,直流侧电压开始出现明显振荡。加入主动阻尼补偿后,直流侧电压振荡消失,四种补偿策略对系统振荡均有明显的抑制效果。对图9所示的直流电压进行FFT分析,对比四种补偿方式的振荡抑制效果。为使不同组的实验结果具有可比性,本文在原有的电压波形上叠加了一个幅值为5的10 Hz正弦信号,以10 Hz交流信号为基波进行FFT分析。观测含量最高的谐波频率附近的谐波含量,对比抑制效果见表2。由表2可见,四种补偿方式都能达到很好的振荡抑制效果。其中,交轴电流补偿法和交轴电压补偿法对谐波的抑制效果优于直轴电流补偿法和直轴电压补偿法,而交轴电流补偿法和交轴电压补偿法对谐波的抑制效果接近。
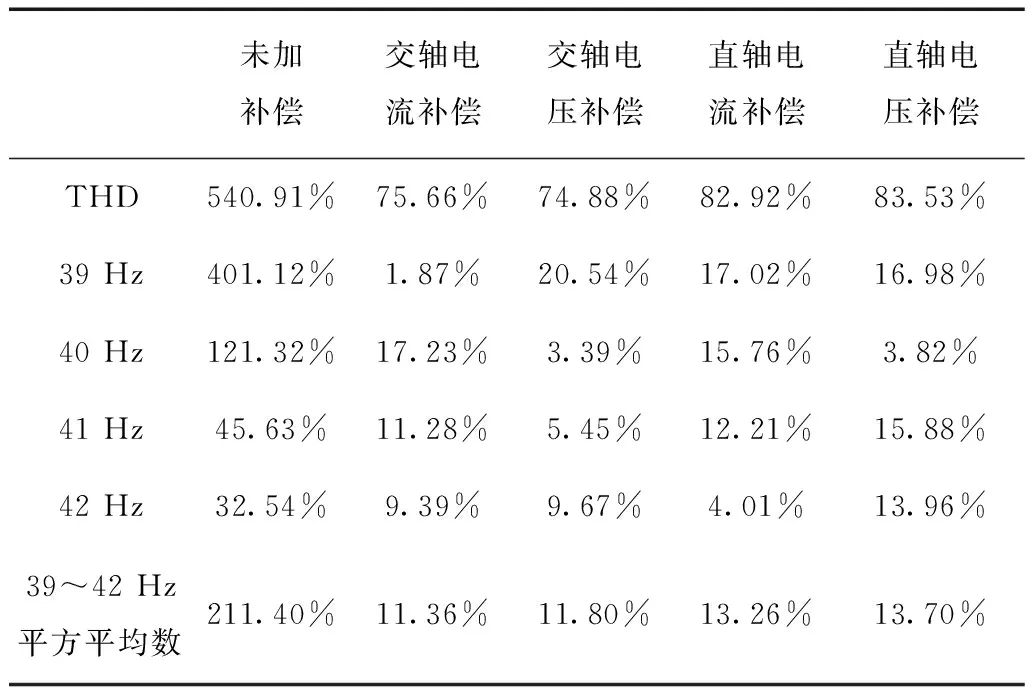
表2 不同阻尼补偿策略谐波含量对比Tab.2 Harmonic content of DC voltage with different compensators
3.2 电流环参数影响对比
图10为未加补偿情况下,采用两组不同的交轴电流调节器PI参数时系统的直流侧电压波形和电机交轴电流波形。
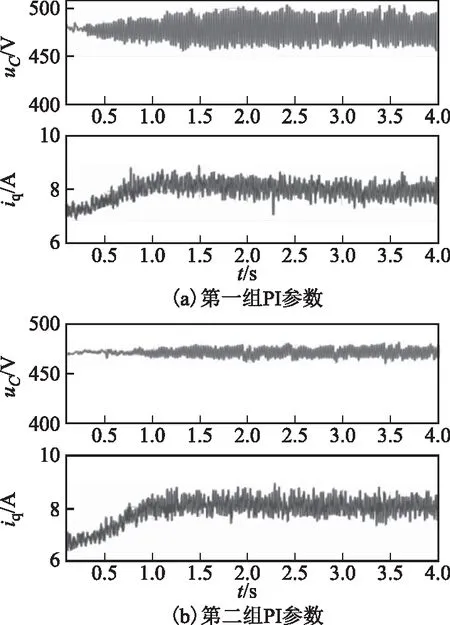
图10 未加补偿且采用不同PI参数时实验波形Fig.10 Experiment results without compensator and with different PI parameters
图11为分别采用上述两组PI参数时,基于交轴电流进行阻尼补偿的直流侧电压和电机交轴电流波形。在两组PI参数下,电流均能快速跟随指令,电机运行良好;且采用第二组PI参数时,系统直流电压振荡幅值相对更小。其中,图11a的PI参数与图9所示实验采用的PI参数相同。

图11 PI参数不同时交轴电流补偿法实验结果Fig.11 Experiment results of q-axis current based compensator with different PI parameters
由图11可见,进行交轴电流补偿后,第二组PI参数下电流响应明显变差。对直流电压进行FFT分析,THD分别为75.66%与141.74%,两者相差66.08%。图12为分别采用上述两组PI参数时,基于交轴电压进行阻尼补偿的直流侧电压和电机交轴电流波形。加入阻尼补偿对电流响应影响并不明显。对直流电压进行FFT分析,THD分别为74.88%与92.77%,两者相差17.89%。
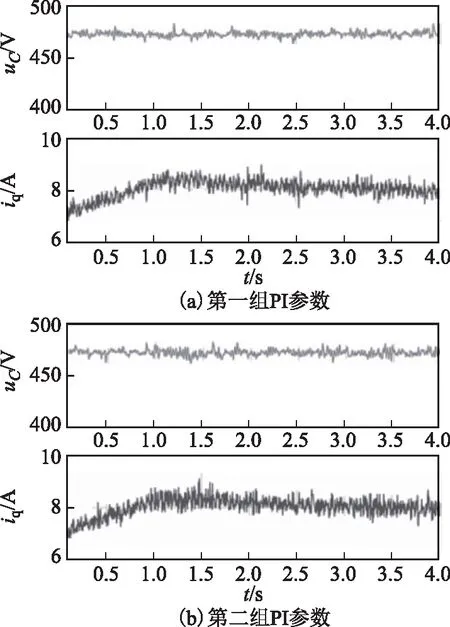
图12 PI参数不同时交轴电压补偿法实验结果Fig.12 Experiment results of q-axis voltage based compensator with different PI parameters
从而验证了,相较于交轴电压补偿法,交轴电流补偿法对交轴电流调节器PI参数的变化相对敏感,系统鲁棒性不如交轴电压补偿法。
实验结果验证了对于双电流调节器控制下的逆变器-IPMSM系统,交轴电压补偿法更为适用。
4 结论
本文针对直流供电逆变器-IPMSM传动系统的阻抗不匹配振荡抑制方法展开研究:推导了双电流调节器控制下逆变器-IPMSM系统输入导纳,为分析系统稳定性提供理论模型;参考异步电机系统振荡抑制方法,依托IPMSM模型,提出直轴电流补偿法、直轴电压补偿法两种主动阻尼补偿方法,丰富了可选择的振荡抑制办法;推导了加入交轴电流补偿法、交轴电压补偿法、直轴电流补偿法、直轴电压补偿法四种主动阻尼补偿方法后的逆变器-IPMSM系统输入导纳,为理论分析补偿方法有效性与进行补偿参数设计提供理论模型;依据IPMSM模型与电机控制模型,提出对于抑制双电流调节器控制下的逆变器-IPMSM系统阻抗不匹配振荡,交轴电压补偿法最为适用。实验验证了四种阻尼补偿方法的有效性和交轴电压补偿法的优势。
[1] Mosskull H,Galic J,Wahlberg B.Stabilization of induction motor drives with poorly damped input filters[J].IEEE Transactions on Industrial Electronics,2007,54(5):2724-2734.
[2] 赵雷廷,刁利军,董侃,等.地铁牵引变流器-电机系统稳定性控制[J].电工技术学报,2013,28(6):101-107.
Zhao Leiting,Diao Lijun,Dong Kan,et al.Research on stabilization control for metro traction converter-motor system[J].Transactions of China Electrotechnical Society,2013,28(6):101-107.
[3] Lee W,Sul S.DC-link voltage stabilization for reduced DC-link capacitor inverter[J].IEEE Transactions on Industrial Applications.2014,50(1):1740-1744.
[4] 方晓春.城轨列车永磁同步牵引电机控制与逆变器直流侧振荡抑制研究[D].北京:北京交通大学,2016.
[5] Maheshwari R,Munk-Nielsen S,Lu K.An active damping technique for small DC-link capacitor based drive system[J].IEEE Transactions on Industrial Applications.2010,9(2):1205-1209.
[6] Mohamed A,Radwan A,Lee T.Decoupled reference voltage based active DC-Link stabilization for PMSM drives with tight-speed regulation[J].IEEE Transactions on Industrial Electronics,2012,59(12):4523-4536.
[7] 高雅,刘卫国,骆光照.牵引机车用永磁同步电机断电-重投控制系统研究[J].电工技术学报,2016,31(6):100-107.
Gao Ya,Liu Weiguo,Luo Guangzhao.Research of power down-rejoining on control system for permanent magnet synchronous motor used in traction engines[J].Transactions of China Electrotechnical Society,2016,31(6):100-107.
[8] 方晓春,胡太元,林飞,等.基于交直轴电流耦合的单电流调节器永磁同步电机弱磁控制[J].电工技术学报,2015,30(2):140-147.
Fang Xiaochun,Hu Taiyuan,Lin Fei,et al.Single current regulator flux-weakening control of PMSM based on the D-Q current cross-coupling effect[J].Transactions of China Electrotechnical Society,2015,30(2):140-147.
[9] Magne P,Marx D,Nahid-Mobarakeh B,et al.Large-signal stabilization of a DC-link supplying a constant power load using a virtual capacitor:impact on the domain of attraction[J].IEEE Transactions on Industrial Applications,2012,48(3):878-887.
[10]Liu Xinyun,Forsyth A,Cross A.Negative input-resistance compensator for a constant power load[J].IEEE Transactions on Industrial Electronics,2007,54(6):3188-3196.
[11]Liutanakul P,Awan A,Pierfederici S,et al.Linear stabilization of a DC bus supplying a constant power load:a general design approach[J].IEEE Transactions on Power Electronics,2010,25(2):475-488.
[12]Maheshwari R,Munk-Nielsen S,Lu K.An active damping technique for small DC-link capacitor based drive system[J].IEEE Transactions on Industrial Electronics,2010,9(2):1205-1209.
[13]Feng Xiaogang,Liu Jinjun,Lee F C.Impedance specifications for stable DC distributed power systems[J].IEEE Transactions on Power Electronics,2002,17(2):157-162.
[14]赵雷廷.地铁牵引电传动系统关键控制技术及性能优化研究[D].北京:北京交通大学,2014.
(编辑 于玲玲)
Comparative Research on DC Side Oscillation Suppression Methods for Inverter-IPMSM System Caused by Impedance Mismatch
FangXiaochunZhongZhihongYangZhongpingLinFei
(School of Electrical Engineering Beijing Jiaotong University Beijing 100044 China)
Due to mismatch of output impedances of LC and input impedance of inverter-motor system,inverter-IPMSM(Interior Permanent Magnet Synchronous Motor) system will lose stability with a large output power.That means DC current and voltage oscillation.For stability analysis,input admittance formulas of inverter-IPMSM system under double current control are derived.Reference induction motor system oscillation suppression methods and combined with IPMSM torque formula,two oscillation suppression methods based ond-axis voltage and current command separately are proposed.These two methods are compared with the existing oscillation suppression methods based on q-axis voltage and current command separately.Input admittance formulas of inverter-IPMSM system with oscillation suppression are derived.The Nyquist theorem is adopted to verify the validity of the oscillation suppression methods.According to the motor model and control system model,the oscillation suppression method based on q-axis voltage is considered to be the best.Experimental verification of the viewpoints is carried out.
Interior permanent magnet synchronous motor(IPMSM),impedance matching,DC side oscillation,damping compensation,oscillation suppression
2016-08-19 改稿日期2016-12-16
10.19595/j.cnki.1000-6753.tces.L70326
TM341
方晓春 男,1987年生,博士,研究方向为电力电子与电气传动。
E-mail:me330221789@163.com(通信作者)
钟志宏 男,1993年生,硕士研究生,研究方向为电力电子与电气传动。
E-mail:15121522@bjtu.edu.cn
