Laval喷管内二氧化碳凝结过程研究

孙文娟， 曹学文， 杨 文， 靳学堂

(1.中国石油大学 储运与建筑工程学院， 山东 青岛 266580； 2.中国石化销售有限公司 华南分公司， 广东 广州 510620)

Laval喷管内二氧化碳凝结过程研究

孙文娟1， 曹学文1， 杨 文2， 靳学堂1

(1.中国石油大学 储运与建筑工程学院， 山东 青岛 266580； 2.中国石化销售有限公司 华南分公司， 广东 广州 510620)

设计Laval喷管结构，结合内部一致经典成核理论和Gyarmathy液滴生长理论，建立超声速凝结相变欧拉双流体数学模型，对超声速流动条件下天然气中二氧化碳气体的凝结过程进行数值模拟研究，并分析入口二氧化碳摩尔分数对凝结过程的影响。结果表明，气体进入喷管后高速膨胀，温度降低，二氧化碳气体在喷管扩张段发生自发凝结现象，凝结核在短距离内急剧产生，液相质量分数持续增加，直至喷管出口；入口气体中二氧化碳摩尔分数从0.05增至0.14，凝结起始位置前移6.82 mm，极限成核率和液滴数量减少，液滴生长速率加快，液滴粒径增加，喷管出口液相质量分数由0.1238增至0.1991；不同入口二氧化碳摩尔分数下喷管出口二氧化碳液化率均高于60%，出口气相中二氧化碳摩尔分数较入口大幅降低，入口二氧化碳摩尔分数小于0.10时，出口均可降低到0.03以下。

Laval喷管； 凝结； 液化； 天然气脱碳； 数值模拟

近年来，天然气工业在改善能源结构、推动低碳经济过程中展现出快速发展的良好态势[1]。随着天然气需求量的迅速增长，天然气净化工业的地位也愈益重要，脱碳工艺是气体净化的重要环节，当天然气中二氧化碳含量超过质量指标时，必须采用合适的方法将其脱除至规定值以内[2]。同时，二氧化碳减排及利用问题越来越受到重视[3]，但目前传统的天然气脱碳方法大多将脱出的二氧化碳直接排放，造成严重的资源浪费和环境污染，不符合节能减排的要求。

超声速旋流分离技术为这一问题提供了新的解决途径，其核心是利用气体高速膨胀产生的低温凝结效应结合旋流分离技术实现混合气体中凝点较高组分的冷凝分离[4]。超声速旋流分离装置具有结构紧凑、无需添加化学药剂、无转动部件等优点[5]，目前在天然气脱水、脱重烃[6-11]及天然气液化领域[12-13]已开展了大量理论及实验研究，若能将其应用到天然气脱碳领域，则可在脱除二氧化碳的同时得到液态二氧化碳产品，实现二氧化碳的回收利用，对于天然气净化行业的节能减排具有重要意义。二氧化碳在喷管内发生凝结液化是实现旋流分离的前提，目前尚未见天然气中二氧化碳在Laval喷管内凝结液化方面的相关报道，笔者主要针对喷管内二氧化碳气体的凝结液化过程进行数值模拟研究，并分析二氧化碳含量波动对其凝结过程的影响。

1 Laval喷管设计

基于流动特征，Laval喷管可分为收缩段(亚声速区)、喉部(临界区)、扩张段(超声速区)三部分[14]，为保证进入喷管的气流均匀，收缩段前需有一定长度的稳定段。考虑真实气体效应，采用BWRS真实气体状态方程计算喉部热力学参数[15]，以确定喉部尺寸；稳定段长度和直径均与喉部尺寸有关，稳定段长度取为喉部直径的10倍左右，稳定段直径取为喉部直径的8倍左右；收缩段设计采用双三次曲线法，该方法能为喉部提供较为均匀的气流，前后两曲线连接点相对坐标取为0.45；扩张段分为圆弧段、直线段和消波段三部分，在加速气流的同时消除膨胀波的影响；考虑黏性作用，从喉部开始进行边界层修正，修正角取0.5°[14]。利用编制的MATLAB程序进行结构设计，喷管型面及尺寸如图1所示。

图1 Laval喷管结构示意图Fig.1 Structural schematic of the Laval nozzle

2 超声速流动凝结相变数学模型

2.1 成核模型及液滴生长模型

2.1.1 成核模型

采用Girshick等[16-17]提出的经Lamanna[18]修正后的内部一致经典成核理论(Internally consistent classical theory，ICCT)计算液滴成核率，表达式见式(1)。

(1)

2.1.2 液滴生长模型

凝结核心形成以后，凝结相变将进入液滴生长阶段，由于凝结核粒径较小，在气流中以相同的速度运动，且由于成核过程极短，所形成凝结核心总数的数量级与气体分子的数量级相比非常小，彼此碰撞的可能性很小，因此目前气体高速膨胀过程中液滴的生长理论不考虑液滴的相互碰撞和聚并，仅考虑单一液滴与周围气体的传质和传热过程[4-5,19]。采用Gyarmathy模型[20]计算液滴生长速率，表达式见式(2)，凝结液滴临界半径采用式(3)计算。

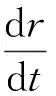
(2)

(3)

2.2 气-液控制方程组

基于欧拉双流体模型，忽略气-液相间速度滑移，建立气、液流动控制方程组，气相流动控制方程包括气相质量守恒方程(见式(4))、二氧化碳气体质量守恒方程(见式(5))、动量方程(见式(6))、能量方程(见式(7))，液相控制方程包括液相质量方程(见式(8))、液滴数目方程(见式(9))、液滴半径方程(见式(10))，诸方程中添加由于凝结相变而产生的源项，源项表达式如式(11)～式(14)所示。

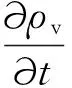
(4)

(5)

(6)

(7)

(8)

(9)

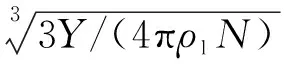
(10)

Sm=-m

(11)

Su=-mui

(12)

Sh=m(hlv-h)

(13)

SY=m

(14)

(15)

2.3 数值计算方法

(1) UDS及UDF：数值计算中，由于气体凝结相变的产生，需要增加液相流动控制方程组，且气、液相流动控制方程组中有源相存在，因此需要对FLUENT进行二次开发。通过用户自定义标量(User-Defined Scalar, UDS)增加液相流动控制方程组，利用C语言编写用户自定义函数(User-Defined Function, UDF)添加诸方程中的源项，气体比热容、黏度、导热系数等参数[21]也利用C语言编写相应的UDF程序，嵌入到FLUENT中进行计算。

(2) 网格划分：采用ANSYS ICEM CFD进行网格划分，采用结构网格，对边界层网格进行加密，为排除计算精度对网格密度的依赖性，进行网格无关性验证，逐步加密网格，最终确定计算网格数为17400。

(3) 湍流模型：为闭合流动控制方程组，需引入合适的湍流方程，选用k-ω湍流模型，该模型包含了可压缩性影响，适用于受到壁面限制的流动。

(4) 求解器及离散化方法：选用基于密度法的求解器，该方法适用于求解可压缩流动；采用二阶迎风格式离散流动方程，采用一阶迎风格式离散湍流动能方程和湍流耗散率方程。

(5) 边界条件：喷管入口设定为压力入口，指定总压、静压、湍流参数(湍流强度和水力半径)、总温、气体组成；出口设定为压力出口，因出口为超声速流动，所有流动参数将从内部外推而得，故不进行相应设置；壁面设定为无滑移、无渗流、绝热边界。

2.4 模型验证

通过空气中水蒸气在Laval喷管内的凝结液化实验验证所建模型，采用压力分布测试系统测量喷管内压力分布，采用多波长消光法颗粒测试系统测量喷管内凝结液滴数目分布。为了便于测量，所用喷管为矩形截面喷管，总长为177.29 mm，喉部尺寸为5.00 mm×8.00 mm，入口尺寸为40.00 mm×8.00 mm，出口尺寸为12.30 mm×8.00 mm。喷管入口压力为7.83×105Pa，入口温度为290.25 K，入口湿度为97.6%。

实验测得喷管内压力及液滴数目分布数据与模拟所得计算结果如图2所示。由图2可知，实验所测喷管内压力变化趋势与数值模拟结果较为吻合，说明所建数学模型对流场预测具有较好的准确性。实验所测喷管内液滴数目变化趋势与数值模拟结果基本一致，液滴生成后数目保持不变，说明模型中忽略液滴碰撞与聚并的假设较为合理；实验数据与模拟结果偏差在2个数量级左右，与目前国内外常用气体凝结参数测试方法结果偏差相当[19,22]，且模拟结果较为准确地捕捉到了凝结起始位置，说明所建数学模型可准确描述喷管内气体的超声速凝结流动过程。

由图2还可知，实验数据与模拟结果仍存在偏差，原因分析如下：(1) Laval喷管扩张段内气流为超声速，测试装置对液滴的捕捉在超声速流动条件下存在一定困难，测量的准确性受到影响；(2) 尽管实验系统中已安装过滤器以防止固体及液体颗粒的携带，但受过滤设备的限制，仍无法完全消除颗粒对自发凝结过程的影响，使得液滴数目存在一定的偏差。

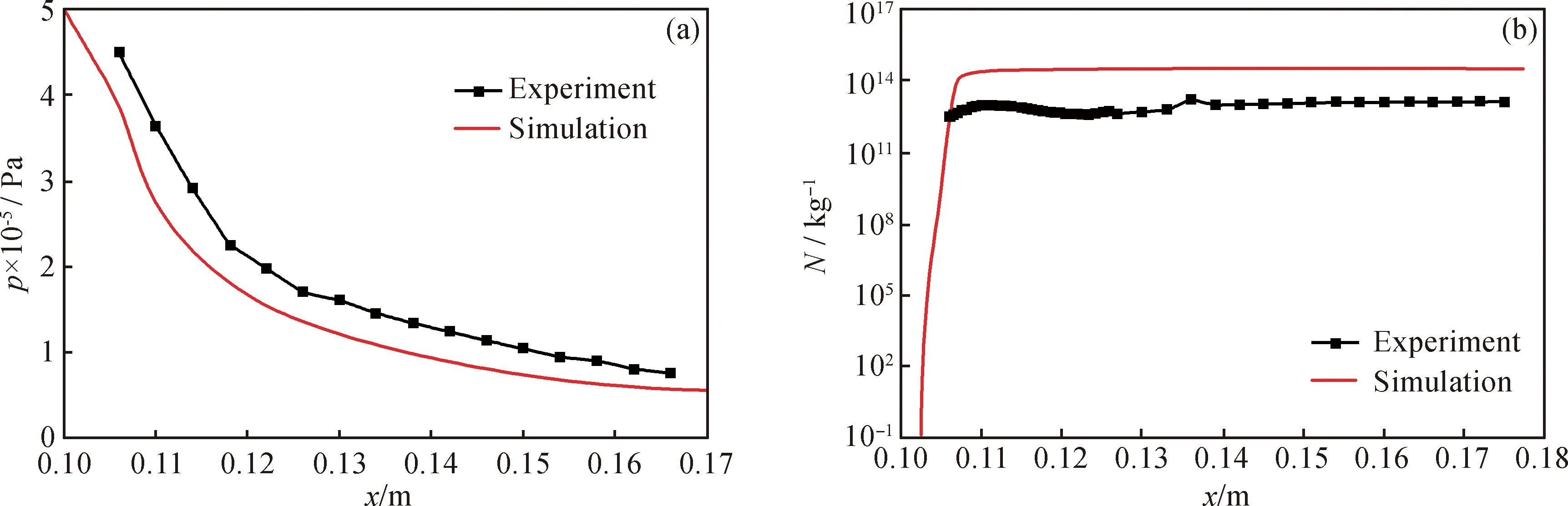
图2 Laval喷管内压力(p)及液滴数目(N)的实验结果与数值计算结果对比Fig.2 The comparison between experimental data and simulation results(a) p; (b) N

3 结果与讨论

3.1 二氧化碳气体凝结过程

天然气是一种包含多种组分的气体混合物，为简化计算，选取天然气的主要成分甲烷和二氧化碳构成的二元系进行研究。采用上述所建凝结相变数学模型，对二氧化碳-甲烷双组分气体在喷管内的凝结流动过程进行模拟计算。入口压力为4×106Pa，入口温度为293.15 K，入口二氧化碳摩尔分数为0.05工况条件下，喷管内气体流动参数及凝结参数分布如图3所示。

由图3可知，甲烷和二氧化碳混合气体进入喷管后高速膨胀，马赫数逐渐增大，压力、温度逐渐降低，过冷度逐渐增大，气体处于极度热力学不平衡状态，在喷管扩张段距离喉部36.77 mm处，二氧化碳气体发生自发凝结现象，大量凝结核在短距离内急剧产生，成核率峰值可达2.366×1027(m-3·s-1)，之后由于凝结潜热的释放，过冷度降低，成核条件不再具备，成核率又急剧下降为0，成核过程结束，液滴数目达到最大值后保持不变。由于壁面摩擦效应的影响，贴近喷管壁面处成核率较喷管中心区域低，如图3(e)所示，使得液滴数目分布呈现出中间数量密度高而贴近壁面处低的规律，如图3(f)所示。由于气体仍处于过冷状态，更多二氧化碳分子将在临界凝结核心表面不断液化，凝结液滴得以继续生长，液相质量分数相应增加，在喷管出口处可达0.1238，为后续的旋流分离脱除创造了条件。

3.2 二氧化碳摩尔分数对凝结过程的影响

为探讨超声速旋流分离脱碳技术对二氧化碳摩尔分数波动的适应性，保持入口温度压力不变，逐渐增加入口气体中二氧化碳摩尔分数，对二氧化碳摩尔分数为0.08、0.10、0.12、0.14的混合气体在喷管内的凝结液化过程进行模拟研究，喷管中心轴线处气体温度、过冷度、成核率、液滴数目、液滴生长速率、液滴半径分布如图4所示。

从图4(a)～图4(c)可见，随着入口气体中二氧化碳摩尔分数的增加，气体将更早达到凝结成核所需要的极限过冷状态，成核起始位置向前移动，当入口二氧化碳摩尔分数为0.08时，成核起始点距离喉部34.29 mm，入口二氧化碳摩尔分数增至0.14时，成核起始点前移至距离喉部29.95 mm处，向前移动了4.34 mm。但由于成核位置越靠近喉部，发生凝结时的温度越高，使得成核率峰值由 8.257×1025(m-3·s-1)降至4.870×1024(m-3·s-1)，凝结液滴数目由3.122×1019kg-1降至1.607×1018kg-1。从图4(d)、图4(e)可以看出，入口二氧化碳摩尔分数较高时，液滴生长速率较大，液滴半径相应增加。由前述分析可知，气体高速膨胀产生的液滴生长过程可忽略液滴间的相互碰撞，仅考虑单一液滴与周围气体的传热传质过程。按气体动力学理论，气体分子的运动是随机的，气体分子与液滴表面的碰撞频率与分子的平均自由程以及液滴半径有关，气体分子平均自由程采用式(16)计算。一般用Knudsen数描述气体分子与液滴碰撞的情况[23]，表达式见式(17)。

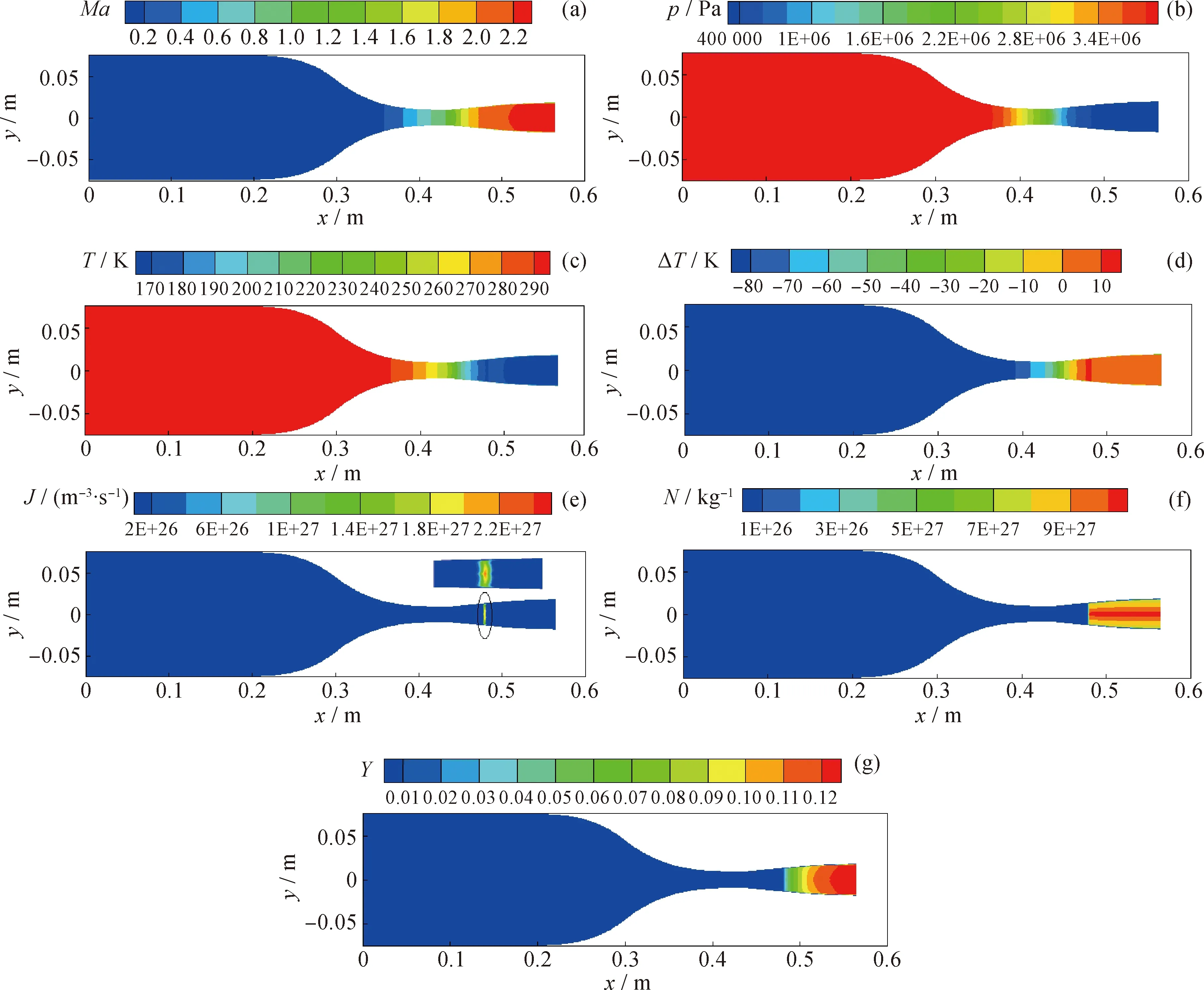
图3 喷管内凝结流动参数分布图Fig.3 Flow and condensation parameters distribution in the nozzle(a) Ma; (b) p; (c) T; (d) ΔT, ΔT=Ts-T; (e) J; (f) N; (g) Y

(16)

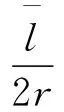
(17)

当二氧化碳摩尔分数增加时，二氧化碳气体分压力增大，气体分子平均自由程减小，Knudsen数减小，液滴粒径相对于周围气体分子来说就越大，二氧化碳气体分子碰撞到液滴的概率增加，使得液滴生长速率加快。

3.3 二氧化碳液化率

随着二氧化碳气体的凝结，液相质量分数增加，气相中的二氧化碳含量随之降低，二氧化碳液化率是影响超声速旋流分离装置脱碳性能的重要参数之一，定义为：

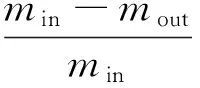
(18)

不同二氧化碳摩尔分数下喷管出口液相质量分数、气相中二氧化碳摩尔分数及液化率如图5所示。从图5(a)可知，虽然入口二氧化碳摩尔分数增多时凝结液滴数量较少，但由于液滴粒径更大，出口液相质量分数仍然有所增加，由0.1238增至0.1991。由图5(b)可知，喷管出口气体中二氧化碳摩尔分数较入口大幅降低，随着入口气体中二氧化碳摩尔分数的增大，出口气体中二氧化碳残余量增多，喷管入口二氧化碳摩尔分数为0.05时，出口气体中二氧化碳摩尔分数可降至0.0009，入口二氧化碳摩尔分数小于0.10时，出口均可降低到0.03以下，达到我国商品天然气的要求。由图5(c)可见，随着入口气体中二氧化碳摩尔分数的增加，二氧化碳液化率呈下降趋势，但不同二氧化碳摩尔分数下喷管均能实现60%以上的液化率。

图4 不同二氧化碳摩尔分数喷管中心轴线处凝结流动参数分布Fig.4 Flow and condensation parameters distribution along nozzle axis with different CO2 mole fractions(a) T, ΔT; (b) J; (c) N; (d) dr/dt; (e) r

4 结 论

(1) 二氧化碳和甲烷混合气体进入Laval喷管后膨胀至超声速，温度降低，在喷管扩张段达到一定过冷度后二氧化碳气体发生凝结成核及液滴生长现象，形成气-液两相流动，随着二氧化碳气体的凝结，气相中的二氧化碳摩尔分数逐渐降低，通过气-液分离可实现二氧化碳的脱除和液体二氧化碳的回收利用。

(2) 对于结构固定的喷管，保持入口压力温度不变，增加入口气体中二氧化碳的摩尔分数将使其更早达到凝结成核所需的临界条件，凝结起始位置前移，成核率峰值及成核数量减少，但液滴生长速率加快，液滴粒径增大，在喷管出口能达到更大的液相质量分数。

(3) 超声速旋流分离脱碳技术对二氧化碳摩尔分数波动具有一定的适应性，不同入口二氧化碳摩尔分数下喷管出口气相中二氧化碳摩尔分数均大幅降低，液化率均高于60%，但出口气体中二氧化碳残余量随入口二氧化碳摩尔分数的增加而增大，为使分离后气体中二氧化碳摩尔分数降至允许范围内，需针对装置操作参数和结构参数进一步开展提高二氧化碳液化率方面的研究，为今后液化分离并回收液体二氧化碳产品装置的研发提供理论基础。

图5 不同二氧化碳摩尔分数喷管出口液相质量分数(Y)、二氧化碳残余量(mout)及液化率(Rl)Fig.5 Liquid mass fraction(Y), CO2 residual quantity(mout) and liquefaction rate(Rl) at the nozzle outlet with different CO2 mole fractions(a) Y; (b) mout; (c) Rl

符号说明：

E——气体总能，J/kg；

h——气体总焓，J/kg；

hlv——凝结潜热，J/kg；

J——成核率，m-3·s-1；

kB——Boltzmann常数，1.3806505×10-23J/K；

keff——有效导热系数，W/(m·K)；

Kn——无量纲Knudsen数；

m——单位时间单位体积内凝结的液滴质量，kg/(m3·s)；

min——入口气体中二氧化碳摩尔分数；

mout——出口气体中二氧化碳摩尔分数；

mv——单个二氧化碳分子质量，kg；

Ma——马赫数；

N——自发凝结液滴数目，kg-1；

p——压力，Pa；

pv——二氧化碳气体实际压力，Pa；

Prv——气体Prandtl数；

r——液滴半径，m；

rc——凝结液滴临界半径，m；

Rl——二氧化碳液化率；

Rv——气体常数，J/(kg·K)；

S——气体过饱和度；

Sh——能量源相，J/(m3·s)；

Sm——质量源相，kg/(m3·s)；

Su——动量源相，kg/(m2·s2)；

SY——湿度源相，kg/(m3·s)；

t——时间，s；

T——气体温度，K；

Ts——气体压力对应的饱和温度，K；

ui，uj——轴向与径向速度，m/s；

x——轴向坐标，m；

xi，xj——轴向与径向位置坐标，m；

y——径向坐标，m；

Y——液相质量分数；

γ——气体比热比；

δij——Kronecker delta数；

ΔT——过冷度，K；

θ——无因次表面张力；

λv——气体导热系数，W/(m·K)；

μ——气体黏度，kg/(m·s)；

ρ——混合相密度，kg/m3；

ρc——二氧化碳气体密度，kg/m3；

ρl——液相密度，kg/m3；

ρv——气相密度，kg/m3；

σ——液滴表面张力，N/m；

τeff——有效应力张量。

[1] 贾承造, 张永峰, 赵霞. 中国天然气工业发展前景与挑战[J].天然气工业, 2014, 34(2): 1-11. (JIA Chengzao, ZHANG Yongfeng, ZHAO Xia. Prospects of and challenges to natural gas industry development in China[J].Natural Gas Industry, 2014, 34(2): 1-11.)

[2] 陈颖, 张雪楠, 梁宏宝, 等. 富含CO2天然气净化技术现状及研究方向[J].石油学报(石油加工), 2015, 31(1): 194-202. (CHEN Ying, ZHANG Xuenan, LIANG Hongbao, et al. Present situation and research directions of purification technology used in natural gas containing rich CO2[J].Acta Petrolei Sinica (Petroleum Processing Section), 2015, 31(1): 194-202.)

[3] 罗金玲, 高冉, 黄文辉, 等. 中国二氧化碳减排及利用技术发展趋势[J].资源与产业, 2011, 13(1): 132-137. (LUO Jinling, GAO Ran, HUANG Wenhui, et al. Carbon dioxide emission reduction and utilization technology in China[J].Resources & Industries, 2011, 13(1): 132-137.)

[4] 马庆芬. 旋转超音速凝结流动及应用技术研究[D].大连: 大连理工大学, 2009.

[5] 文闯. 湿天然气超声速旋流分离机理研究[D].青岛: 中国石油大学, 2014.

[6] 文闯, 曹学文, 张静, 等. 基于旋流的天然气超声速喷管分离特性[J].石油学报(石油加工), 2011, 27(1): 150-154. (WEN Chuang, CAO Xuewen, ZHANG Jing, et al. Separation characteristics of supersonic swirling flow nozzle for natural gas[J].Acta Petrolei Sinica (Petroleum Processing Section), 2011, 27(1): 150-154.)

[7] 温艳军, 梅灿, 黄铁军, 等. 超音速分离技术在塔里木油气田的成功应用[J].天然气工业, 2012, 32(7): 84-86. (WEN Yanjun, MEI Can, HUANG Tiejun, et al. Application of supersonic separator technology in the Tarim Oil Field[J].Natural Gas Industry, 2012, 32(7): 84-86.)

[8] MACHADO P B, MONTEIRO J G M, MEDEIROS J L, et al. Supersonic separation in onshore natural gas dew point plant[J].Journal of Natural Gas Science and Engineering, 2012, 6: 43-49.

[9] SHOOSHTARI S H R, SHAHSAVAND A.Predictions of wet natural gases condensation rates via multi-component and multi-phase simulation of supersonic separators[J].Korean Journal of Chemical Engineering, 2014, 31(10): 1845-1858.

[10] HAGHIGHI M, HAWBOLDT K A, ABDI M A. Supersonic gas separators: Review of latest developments[J].Journal of Natural Gas Science and Engineering, 2015, 27(1): 109-121.

[11] CAO Xuewen, YANG Wen. The dehydration performance evaluation of a new supersonic swirling separator[J].Journal of Natural Gas Science and Engineering, 2015, 27(3): 1667-1676.

[12] 杨文, 曹学文, 徐晓婷, 等. 高速膨胀天然气凝结流动特性[J].石油学报(石油加工), 2016, 32(1): 73-81. (YANG Wen, CAO Xuewen, XU Xiaoting, et al. Flow and condensation characteristics of natural gas with high speed expansion[J].Acta Petrolei Sinica (Petroleum Processing Section), 2016, 32(1): 73-81.)

[13] 杨文, 曹学文, 王迪, 等. 提高喷管内天然气液化效率的方法[J].石油学报(石油加工), 2016, 32(2): 277-288. (YANG Wen, CAO Xuewen, WANG Di, et al. Methods of improving the natural gas liquefaction efficiency in nozzle[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2016, 32(2): 277-288.)

[14] 易仕和, 赵玉新, 何霖, 等. 超声速与高超声速喷管设计[M].北京: 国防工业出版社, 2013.

[15] 李震东. 超音速旋流分离器喷管设计与相变特性研究[D].青岛: 中国石油大学, 2006.

[16] GIRSHICK S L, CHIU C P. Kinetic nucleation theory: A new expression for the rate of homogeneous nucleation from an ideal supersaturated vapor[J].The Journal of Chemical Physics, 1990, 93(2): 1273-1277.

[17] GIRSHICK S L. Comment on: Self-consistency correction to homogeneous nucleation theory[J].The Journal of Chemical Physics, 1991, 94(1): 826-827.

[18] LAMANNA G. On nucleation and droplet growth in condensing nozzle flows[D].Netherlands: Eindhoven University of Technology, 2000.

[19] 蒋文明. 多组分凝结性超音速流传热传质理论及实验研究[D].北京: 北京工业大学, 2010.

[20] GYARMATHY G. Grundlagen einer theorie der nassdampfturbine[D].Zürich: Eidgenoessische Technische Hochschule Zuerich, 1962.

[21] 童景山.流体热物性学[M].北京: 中国石化出版社, 2008.

[22] WOLK J, STREY R. Homogeneous nucleation of H2O and D2O in comparison: The isotope effect[J].Journal of Physical Chemistry B, 2001, 105(47): 11683-11701.

[23] 蔡颐年, 王乃宁. 湿蒸汽两相流[M].西安: 西安交通大学出版社, 1985.

Study on the Carbon Dioxide Condensation Process in a Laval Nozzle

SUN Wenjuan1, CAO Xuewen1, YANG Wen2, JIN Xuetang1

(1.CollegeofPipelineandCivilEngineering,ChinaUniversityofPetroleum,Qingdao266580,China;2.SouthChinaBranch,SINOPECSalesCo.Ltd.,Guangzhou510620,China)

The Laval nozzle was designed and an Euler-Euler two-phase flow mathematical model was developed to simulate the spontaneous condensation process of carbon dioxide from natural gas in the supersonic condition using the internally consistent classical theory and the Gyarmathy model. The effect of carbon dioxide mole fraction on the condensation process was also analyzed. The results showed that carbon dioxide gas condensed spontaneously in the divergent section of the nozzle due to the refrigeration effect caused by supersonic expansion. The condensation nuclei were generated intensively within a narrow distance. The mass fraction of liquid phase would continue increasing until the nozzle outlet. When the mole fraction of the carbon dioxide in the inlet gas stream increased from 0.05 to 0.14, the nucleation process moved forward by 6.82 mm with decreasing maximum nucleation rate and droplet number. However, the droplet radius increased as a result of a larger droplet growth rate, and the liquid mass fraction at the nozzle’s exit rose from 0.1238 to 0.1991. The carbon dioxide liquefaction rate was higher than 60% and the carbon dioxide mole fraction in the outlet gas stream significantly decreased for various carbon dioxide mole fractions at the nozzle’s entrance. The mole fraction of carbon dioxide inside the natural gas stream at the outlet was lower than 0.03 when the inlet mole fraction was less than 0.10.

Laval nozzle; condensation; liquefaction; natural gas decarburization; numerical simulation

2016-09-09

国家自然科学基金项目(51274232)和中央高校基本科研业务费专项资金项目(16CX06004A)资助

孙文娟，女，博士研究生，从事天然气加工与处理技术研究

曹学文，男，教授，博士，从事天然气加工与处理技术研究；E-mail:caoxw2004@163.com

1001-8719(2017)04-0763-08

TE645

A

10.3969/j.issn.1001-8719.2017.04.022