区域天顶对流层延迟时空变化特性及其建模研究
2017-08-31费添豪
尹 晖,费添豪
(武汉大学 测绘学院,湖北 武汉 430079)
区域天顶对流层延迟时空变化特性及其建模研究
尹 晖,费添豪
(武汉大学 测绘学院,湖北 武汉 430079)
介绍几种常用的全球对流层延迟改正模型和几种区域对流层延迟模型的建立方法,再利用美国密歇根州的8个测站天顶对流层延迟数据对天顶对流层延迟进行研究,得出天顶对流层延迟在时间尺度及空间尺度上的变化规律,与经度和纬度相关性一般,与高程强相关。通过美国密歇根州的4个测站数据分别计算3种区域对流层延迟模型,得出各个模型的精度,并比较它们的优劣,结论是一次线性插值模型是三者中精度最高的模型。
天顶对流层延迟;时空变化特性;区域拟合模型
对流层延迟是限制全球定位系统精度的重要原因之一,对流层延迟是指电磁波信号在传播过程中穿越高度为50 km以下空间范围内所收到的信号延迟,主要由干延迟和湿延迟组成,其中干延迟易建立比较精确的模型,湿延迟没有明显的规律,建模较为复杂[1]。目前常用的对流层延迟模型大部分都是全球性模型,如需要气象参数的霍普菲尔德(Hopfield)、萨斯塔莫宁(Saastamoinen)和勃兰克(Black)等模型以及不需要气象参数的EGNOS、UNB3等模型,但上述模型在局部地区的测量中精度不是很理想[2]。
近年来,随着CORS系统的广泛使用及高精度定位需求的不断增加,对流层延迟改正量的精确获取成为亟需解决的问题。本文首先简要介绍霍普菲尔德(Hopfield)模型和几种区域对流层延迟建模方法,利用美国密歇根州8个测站相对天顶对流层延迟时间间隔为1 s的数据,对其天顶对流层延迟进行分析研究,得出天顶对流层延迟在时间尺度及空间尺度上的变化规律。其次利用了美国密歇根州4个测站的相对天顶对流层延迟数据分别采用3种区域对流层延迟模型进行了编程计算,分析比较各个模型验证站天顶对流层延迟计算值与真值之差的RMS来反映其拟合程度,以此作为评判模型优劣的标准。从而为选择合适的区域对流层延迟模型提供参考。
1 常用对流层延迟改正模型
1.1 霍普菲尔德(Hopfield)模型
(1)
(2)
(3)
式中:k1,k2和k3为常参数(K2/mbar),k1=77.6,k2=71.6,k3=3.747×105;P0为地面气压,T0为地面温度,ew为地面水汽压,H为测站大地高(m)。Hd为干大气层顶高(m),Hw为湿大气层顶高(m)。Hd,Hw,ew取值如下:
Hd=40 136+148.72(T0-273.16),
(4)
Hw=11 000,
(5)
(6)
实际计算中,通常取标准气压温度和温度为P0=1 013.25 mbar,T0=293.15 K,相对湿度RH=0.5。
1.2 萨斯塔莫宁(Saastamoinen)模型
在建立Saastamoinen模型时,一般将对流层分为两部分,第一部分是从地面到高程约12 km处的对流层顶部,它的温度与高程成反比,通常高程每升高1 000 m温度就会降低6.5度;第二部分是指从对流层顶部一直到50 km处的平流层顶这一范围,可以认为在这一部分中温度不变[4]。
Saastamoinen模型的计算公式如下:
(7)
其中:φ为纬度值,δR为由路径弯曲所造成的延迟的改正项,其值为E和hs的列表函数,hs为测站高程(km),B为hs的列表函数,W(φ·H)为纬度和高程的函数,
W(φ·H)=1+0.002 6 cos 2φ+0.000 28hs.
(8)
经过数值拟合后上述公式可以表示为
(9)
式中:es为水汽压,
es=RHexp(-37.246 5 +0.213 66T-
0.000 256 908T2).
(10)
RH为相对湿度,
RH=RH0exp[-0.000 639 3(H-H0)]=
0.5exp[-0.000 639 3(H-H0)].
(11)
RH0为参考站高程H0处的相对湿度。一般情况下取H0为0,RH0=50%。
1.3EGNOS模型
欧盟为了更便利地解得对流层延迟,建成了无需输入实测气象数据就能计算出精度不低的对流层延迟的EGNOS模型。该模型提供5个气象参数:大气压、大气温度、水汽压、水汽梯度和温度梯度。在海平面处的5个气象元素仅和测站纬度和年积日相关,可由气象资料拟合求得其相关函数模型[5-6]。
在知道了测站处于海平面处的对流层延迟之后结合测站高程可以求出测站处的对流层延迟,其公式如下:
(12)
(13)

(14)
(15)
式中:gm=9.784 m/s2,k1=77.604 K/mbar,k2=377 600 K2/mbar,p为海平面处的大气压(mbar),e为海平面处的水汽压(mbar)。
可以用下面公式来计算测站平均海平面处气象参数
(16)
其中,ξ(φ,D)是关于5个气象参数的函数,只与测站所在的纬度φ和年积日D相关;北半球Dmin=28,南半球Dmin=211;ξ0(φ)为各气象参数的年平均值;Δξ0(φ)为各气象参数的季节变化值。
2 区域对流层延迟建模方法
2.1 反距离加权模型
反距离加权内插模型是一种确定性插值方法,是利用相近的地方有相似的性质的原理,相距越近的两个点越相似,每个内插点都会受到附近点的影响,这种影响会随着数据点和内插点之间距离的增大而逐渐变小,而且在一定范围之外,其影响可以忽略不计[7]。但是,普通的反距离加权法有一些不足的地方,反距离加权的内插曲面的导数在数据点处趋于无穷大,由于加权平均的原因,某些数据细节会丢失。所以采用改进反距离加权法来消除上述模型的不足,也就是用距离倒数的p次幂当做权来计算[8]。公式如下:
(17)
式中:n为数据点个数,xi,yi为数据点i的高斯平面坐标,其值可由高斯投影正算即由大地坐标B,L导出高斯平面坐标(x,y)[9],D为内插点的延迟值,D(xi,yi)为i点的天顶对流层延迟值,pi为i点的权,计算公式如下:
(18)
当式中p=1时,即为反距离加权模型,当p不等于1时为改进的反距离加权模型,si为i点到内插点之间的几何距离。
2.2 一次线性插值模型
一次线性插值是将天顶对流层延迟值与位置呈线性关系的基础上建立的,其公式为
D=a0+a1x+a2y.
(19)
其中:D为天顶方向对流层延迟值,a0,a1,a2为3个拟合系数,x为测站高斯平面横坐标,y为测站高斯平面纵坐标[10]。
2.3 与高程相关的一次曲线拟合模型
若天顶对流层延迟与经纬度相关性不大,但与高程呈强相关,那么可以用仅与高程相关的一次曲线拟合模型,其公式如下:
D=a0+a1H.
(20)
式中:D为测站天顶对流层延迟值,a0,a1为两个拟合系数,H为测站大地高。此模型只顾及到天顶对流层延迟值与测站高程的关系,却没有顾及对流层延迟与经纬度的关系,比较适合较小的测量区域的模型建立,它的优势在于需要的已知测站点较少,只需要两个就行。
3 天顶对流层延迟时空变化特性
本文的数据是采用美国密歇根州2016年3月5日的8个测站相对天顶对流层延迟时间间隔为1 s的数据,图1为测站的点位分布图。
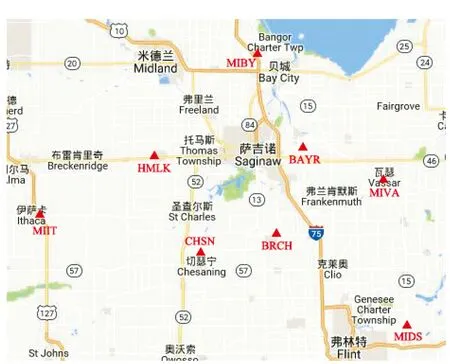
图1 测站的点位分布图
首先将各测站的相对对流层延迟的时间序列用图表示出来,观察分析其随时间的变化规律。再根据这些测站的经度、纬度、高程和天顶方向对流层延迟值可以算出纬度与天顶方向对流层延迟、经度与天顶方向对流层延迟、高程与天顶方向对流层延迟值的相关系数,从而得出天顶对流层延迟的空间变化规律。
3.1 天顶对流层延迟随时间的变化规律
选取BAYR站为基准站,可以画出其他各个测站相对于BAYR基准站相对天顶对流层延迟随时间变化图如图2所示。
计算得出各基站相对于BAYR延迟偏差的RMS如表1所示。

表1 各基站相对于BAYR延迟值的RMS mm

图2 各测站相对于BAYR的ZTD随时间变化图
上面各个基站随时间上的变化规律可以看出各基站某些时间的变化趋势都表现出一致性,而表1也给出了各基站相对于BAYR天顶对流层延迟值偏差的RMS,可以看出每个基站偏差的RMS都小于5 mm,由此可以表明所给的天顶对流层延迟数据有比较高的精度。
3.2 天顶对流层延迟随空间的变化规律
为了分析天顶对流层延迟跟空间相关的关系,将所给的7个测站相对于BAYR的相对天顶对流层延迟值进行分析,首先将每个基站的每天的数据求得其平均值,并将其相对坐标和天顶方向对流层延迟统计到表2中。
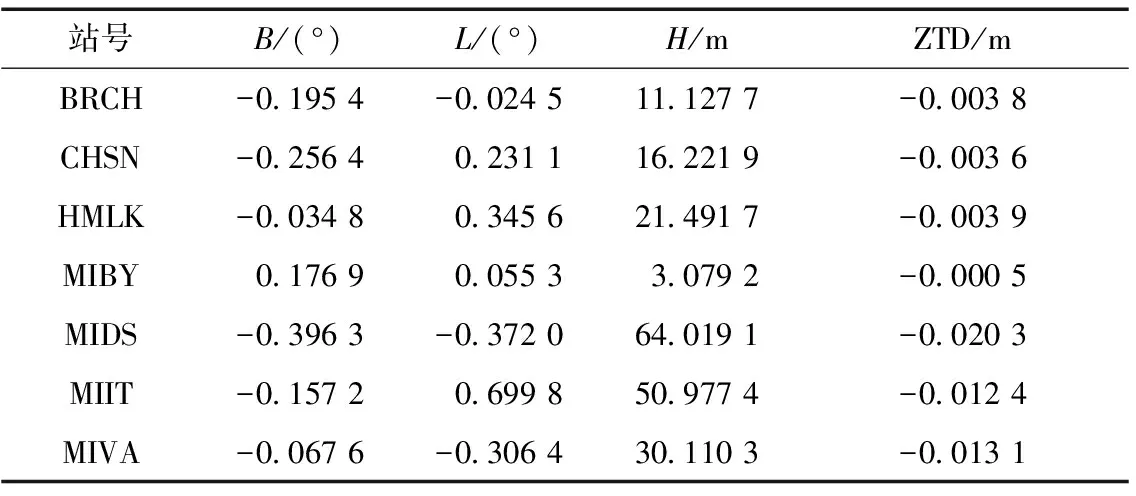
表2 各基站相对BAYR的经纬度高程以及ZTD
利用MATLAB求出表2中矩阵的相关系数矩阵如下:

(21)
从结果中可以看出,各测站ZTD与测站纬度的相关系数是0.665 8,与测站经度的相关系数是0.302 9,与测站高程的相关系数是-0.951 5。由此可以得出结论:测站天顶方向的对流层延迟与纬度的相关性一般,与经度几乎不相关,与高程呈负相关,由此也能看出与高程相关的一次曲线拟合模型可行。
4 区域对流层延迟模型的比较分析
4.1 算法流程
3种模型都是使用几个已知站的数据进行拟合,求解出系数后,再将一个未参与拟合的基站的数据作为验证站来检验模型的优劣。其中反距离加权模型是将验证站到各已知站的距离的倒数作为权,通过式(17)就能计算出模型内插出的验证站处的相对天顶对流层延迟值,再与已知值进行对比。
一次线性插值模型的算法思想是先将各基站坐标(X,Y,Z)通过坐标转换转化到大地坐标系下的(B,L,H),然后再将大地坐标系坐标(B,L,H)通过高斯正算投影到高斯平面上,将各已知站的数据代入式(19),采用最小二乘法平差后可以得到a0,a1,a2为3个拟合系数,将验证站投影到高斯平面的坐标代入式(19)即可得到模型在验证站处的天顶对流层延迟值,与实测值对比。
与高程相关的一次曲线模型是现将各测站的坐标转化成大地坐标系坐标,得到其大地高后,将其代入到式(20)中,用最小二乘法解得a0,a1两个拟合系数,最后将验证站的高程代入求得验证站处的天顶对流层延迟计算值,并与实测值进行比较。
4.2 数据分析
本文利用美国密歇根州2015年6月12日的4个测站时间间隔为5 s的数据拟合来比较一下各个模型的优劣。各测站的点位分布如图3所示,各测站的基本信息如表3所示。

图3 各测站点位分布
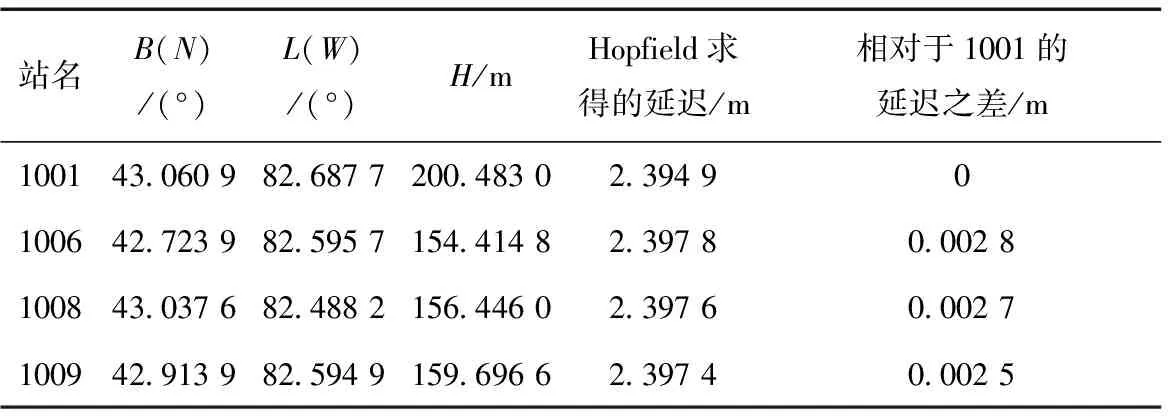
表3 各基站的信息
将各个模型的计算结果用excel作出模型值与实测值的比较图,其中反距离加权模型计算的结果如图4所示,一次线性插值模型计算结果如图5所示,一次曲线拟合模型计算结果如图6所示。

图4 1009站实测相对ZTD值和反距离拟合值比较

图5 1009站实测相对ZTD值和一次线性插值比较

图6 1009站实测相对ZTD值和一次曲线拟合值的比较
最后计算出各个模型在验证站处偏差的RMS如表4所示。
由4表可以看出,3种模型中最优的模型为一次线性插值模型,其次为一次曲线拟合模型,精度最差的为反距离加权模型,其中一次线性插值模型既考虑到了平面位置对天顶对流层延迟的影响,也顾及到了高程相对于天顶方向对流层延迟的影响,所以精度最高,然而一次曲线拟合模型仅顾及到了天顶对流层延迟与测站高程之间的关系,却没有考虑到平面位置对天顶对流层延迟的影响,因此精度较差。

表4 3种模型计算的1009站偏差的RMS mm
5 结 论
本文通过分析多个基站的对流层延迟数据,得到对流层延迟的时空特性,并在此特性的基础上,采用3种比较常用的模型来计算数据,并评定各种模型的精度。通过数据分析可以看出,一次线性插值模型是三者中精度最高的模型,因此在区域对流层延迟解算中一次线性插值模型是在3个模型中比较好的选择。
[1] 李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2010.
[2] 刘立龙,黄良柯,姚朝龙,等.基于区域CORS网天顶对流层延迟4D建模研究[J].大地测量与地球动力学,2012,32(3):45-49.
[3] 陈招华.区域精密对流层延迟建模[D].长沙:中南大学,2010.
[4] 董春来,李传奇,蒋廷臣.对流层延迟改正模型的敏感性分析[J].测绘通报,2014(9):70-72.
[5] 王兴,高井祥,李增科,等.EGNOS模型在对流层延迟插值方法改进中的应用[J].测绘科学技术学报(信息科学版),2015,32(4):353-356.
[6] 赵岩.区域对流层延迟建模分析[D].长沙:中南大学,2013.
[7] 夏元平,吴友平,张静.对流层延迟改正内插方法的比较[J].北京测绘,2007(4):25-27.
[8] 靳国栋,刘衍聪,牛文杰.距离加权反比插值法和克里金插值法的比较[J].长春工业大学学报,2003,24(3):53-57.
[9] 孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社,2010.
[10] 邱蕾,罗和平,王泽民.GPS网络RTK流动站的对流层内插改正分析[J].测绘工程,2011,20(5):70-73.
[11] 姚宜斌,张瑞,易文婷,等.一种新的区域对流层拟合模型及其在PPP中的应用[J].武汉大学学报,2012,37(9):1024-1027.
[责任编辑:刘文霞]
Space-time variation characteristics and model of regional zenith tropospheric delay
YIN Hui,FEI Tianhao
(School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China)
This paper introduces several commonly-used global troposphere delay correction models and the methods of several regional tropospheric delay models. The eight station data of zenith tropospheric delay from Michigan are studied, with a conclusion that the zenith tropospheric delay in the time scale and the change regularity of spatial scales, correlate less with latitude and longitude than the elevation. The four station data from Michigan are calculated respectively on three regional tropospheric delay models. The precision of each model is obtained and compared with its advantages and disadvantages, the conclusion is that a linear interpolation model is the highest of the three precision models.
zenith tropospheric delay(ZTD);temporal and spatial variation characteristics;regional fitting model
著录:尹晖,费添豪.区域天顶对流层延迟时空变化特性及其建模研究[J].测绘工程,2017,26(11):1-5,11.
10.19349/j.cnki.issn1006-7949.2017.11.001
2016-10-17
国家自然科学基金资助项目(51077105);国家电网公司总部科技资助项目(SGSX0000YJJS(2014)457);国家电网公司科技攻关团队资助项目(SG11013)
尹 晖(1962-),女,教授,博士.
P258
A
1006-7949(2017)11-0001-05
