多阶段递进式预测模型在基坑变形中的应用研究

周永胜

(陕西铁路工程职业技术学院,陕西 渭南 714000)

多阶段递进式预测模型在基坑变形中的应用研究

周永胜

(陕西铁路工程职业技术学院,陕西 渭南 714000)

为实现对基坑变形的高精度预测，提高预测结果的稳定性,采用支持向量机、BP神经网络及GM(1,1)作为基础预测模型，并建立了对应各模型参数优化的一阶递进预测模型。以一阶递进预测结果为基础，构建了多种定权与非定权的二阶组合预测模型；以马尔可夫链理论为基础，建立了三阶递进的误差修正模型，实现了对基坑变形的多阶段递进式预测。结果表明：通过各阶段的递进预测，预测精度及稳定性都有了很大的提高，验证了递进预测思路的有效性和可行性。通过对基坑变形的递进式预测研究，以期为基坑的变形提供一种新的思路。

基坑；递进预测模型；支持向量机；BP神经网络；GM(1,1)模型；组合预测；误差修正

1 研究背景

基坑是城市建设中常遇的工程建设之一，由于其所处的环境较为复杂，在施工过程中，基坑会出现不同程度的变形。为避免基坑变形造成严重的工程事故，应对基坑的变形进行监测，尽可能地在后续对其进行变形预测，进而便于采取相应的应对措施。

许多学者已在这方面进行了研究，并取得了一定的成果，如：杨爱婷等[1]采用ACO-BP神经网络对基坑的变形进行预测，结果表明该预测模型对基坑变形的预测精度较高；曹净等[2]则将最小二乘支持向量机(LSSVM)引入到基坑的变形预测中，并结合小波变换和时间序列建立了基坑的综合变形预测模型，通过实例验证了该模型的有效性和可行性；李莉等[3]则将GM(1,1)模型引入到基坑的变形预测中，并采用多种方法对该模型进行优化，很大程度上提高了预测精度，工程价值较为明显。同时，组合预测模型也被广泛的应用到了基坑的变形预测中，如石星照等[4]采用灰色关联定权的方法对单一模型的预测权值进行求解，得出组合预测模型具有更好的稳定性和准确性；钱大林等[5]、任丽芳等[6]则将神经网络的定权模式引入到基坑的组合变形预测过程中，实例验证其能较好地预测基坑的变形。

上述基坑的变形研究均未综合将多种预测模型引入到基坑变形预测过程中，也未研究递进式预测模型在基坑变形预测中的效果。因此，本文以支持向量机(SVM)、BP神经网络及GM(1,1)预测模型为基础，构建多阶段的基坑变形预测模型，并分阶段探讨其预测效果，以期为基坑的变形预测提供一种思路。

2 基本原理

2.1 建模思路

本文期望构建基坑变形的递进预测模型，对基坑的变形进行预测，主要的步骤为：

(1) 以支持向量机、BP神经网络及GM(1,1)为单一预测模型，并利用最小二乘优化、蚁群算法及参数修正，对3种预测模型进行一阶递进优化。

(2) 利用特尔菲法和变异系数法的定权组合模型、误差倒数法和BP神经网络的非定权组合模型，对单一一阶递进预测结果进行组合预测，实现对基坑变形的二阶递进预测。

(3) 利用马尔可夫链对最优的二阶递进预测模型结果进行误差修正优化，实现三阶递进预测。

(4) 对比本文不同阶段的预测结果，验证本文预测模型的有效性。

通过多阶段的递进预测，旨在探讨不同预测模型在基坑变形中的适用性及本文预测思路的可行性和有效性。

2.2 一阶递进预测模型

在一阶递进预测过程中，共应用了支持向量机、BP神经网络及GM(1,1)模型，并对其采取了相应的优化措施。

2.2.1 支持向量机

支持向量机可以利用非线性的映射关系，将输入信息投射到高维空间，并结合相应的风险最小原则和缩小模型的误差边界，实现对样本的非线性预测，具有较高的预测精度。但支持向量机在预测过程中，需要进行二次规划，因此本文选用最小二乘法对其二次规划进行线性处理，以达到优化的目的。而最小二乘支持向量机是将预测样本表示为(xi,yi)，其线性回归可表示为

(1)

式中：w为权值系数；b为常值偏差。

基于风险最小原则，可将回归问题转变为

(2)

式中：c为惩罚因子；ξi为松弛因子。

而其约束条件为

(3)

同时，最小二乘支持向量机的核函数选用径向基函数，可将其表示为

(4)

式中K(x,xi)为核函数。

进而结合求解约束条件，可将LSSVM的预测函数模型表示为

(5)

式中δi为拉格朗日乘子。

2.2.2 BP神经网络

BP神经网络是通过正向传播和反向传播不断反复，实现误差权值的反馈调节，若输入层为X=(x1,x2,…,xn)T(n为输入层节点个数)；输出层为yk(m为输出层节点个数)；隐含层为xj(n1为隐层节点个数)，其传播过程可表示为[7]：

(6)

(7)

式中：wjk为输出层与隐含层对应节点间的权值；wij为输入层与隐含层对应节点间的权值；Qk为输出层对应节点的阈值；Qj为隐含层对应节点的阈值。

在BP神经网络的训练过程中，采用Newton对权值进行修正，表示为

(8)

式中：J为雅可比矩阵；I为初始迭代矩阵；E为误差向量;u为误差修正参数。若式(8)中的u足够大时，可将误差的修正公式进一步表示为

(9)

通过上式不断地对训练中的误差进行修正，直到误差满足期望要求，而其输出误差可表示为

(10)

式中dk为第k节点处的实测样本值。

但BP神经网络的收敛速度较慢，且易陷入局部极小的问题，影响了BP神经网络的预测精度，因此本文采用蚁群算法对其进行优化。其思路是利用蚁群算法对连接权值进行优化学习，获得最优权值，进而达到对网络结构的全局优化。

2.2.3 GM(1,1)模型

若具有n个样本组成的序列为x(0)，表示为[8]

(11)

为消除原始样本的波动性和随机性，对x(0)(k)进行一阶累加，得到序列x(1)(k)，并表示为

(12)

其中，对应节点数据为

(13)

对x(1)(k)序列建立一阶微分方程,即

(14)

式中a和b为系数，可以通过最小二乘法计算得到。

当得到参数a和b后，可完整表示灰色理论的时间响应序列，并将预测值表示为

(15)

但该模型存在预测精度较差，效果不佳的特点。为克服该缺点，采用最小二乘法的基本原理，对初始值进行优化，并利用改进背景值的方法，实现对预测过程中参数的优化，进而达到对模型的优化处理。2.2.3.1 二阶递进预测模型

考虑到一阶递进预测仍具有精度不高的缺点，为提高基坑变形预测的精度及稳定性，在二阶递进预测阶段，采用组合预测的方法对一阶预测的结果进行组合，以期提高预测精度。

在组合预测的过程中，共采用了定权组合和非定权组合2种模式，其中定权主要包含了特尔菲法和变异系数法，而非定权主要包含了误差倒数法和BP神经网络。

二阶递进预测旨在避免单一预测结果的不稳定性，提高预测结果的精度及其可靠性。

2.2.3.2 三阶递进预测模型

三阶递进预测模型主要是对前一阶段预测结果的预测误差进行修正，采用的方法是马尔可夫链误差修正法(MC误差修正法)。其思路是将预测值的相对误差进行划分，共划分为n个区间，即S=[S1，S2，…，Sn]，并将由状态Si经过m步转变到Sj状态的概率表示为[9-10]

(16)

式中：Mij(m)为状态转移所需的次数；Mi为Si状态的个数。

(17)

式中：F(x)为修正后预测值；f(x)为预测值；ΔU，ΔD分别为预测相对误差的上、下限；Δ*为平均相对误差。

另外，由于二阶递进预测结果之间具有一定的差异性，因此，本文只选取组合预测过程中最优的预测结果进行误差修正。

表1 一阶递进预测结果统计

注：1个测量周期为2 d

3 实例分析

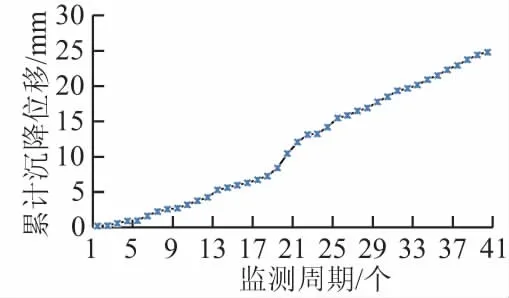
图1 基坑沉降变形曲线Fig.1 Curve of foundation pit’s settlement

为验证本文预测模型的有效性，以文献[1]为实例分析来源，对其基坑变形数据进行预测。由文献[1]可知，基坑的变形数据类型为沉降变形，共监测了40个监测周期，每个监测周期是2 d，其变形曲线如图1所示。同时，基坑的最大沉降速率为2.04 mm/d，最小沉降速率为0.05 mm/d，平均沉降速率为0.621 mm/d。

3.1 一阶递进预测

结合本文的预测思路，首先对基坑的变形进行一阶递进预测，预测结果统计如表1所示。

由表1可以知道，支持向量机、BP神经网络、GM(1,1)这3种不同预测模型的结果具有一定的差异，但一阶递进优化均比传统预测模型不同程度的提高了预测精度，且传统预测模型的相对误差精度多集中在3%～4%之间，而一阶递进预测模型的相对误差多集中在2%～3%之间。为进一步分析不同预测模型及一阶递进预测的效果，以相对误差绝对值的期望和方差为指标，评价两者之间的差异，结果见图2。

图2 相对误差期望对比Fig.2 Comparison of expected relative error between conventional prediction and first-order progressive prediction

由图2可知，通过一阶递进预测，3种预测模型的预测精度均表现出不同程度的提高。其中，在传统预测过程中，BP神经网络和GM(1,1)模型的预测精度相当，并优于支持向量机预测模型;而在一阶递进预测过程中，ACO-BP神经网络模型的预测精度最高，其次是LSSVM模型和优化GM(1,1)模型，但三者之间的差异均不大。对比一阶递进前后的预测精度，得出各模型的优化效果具有一定的差异，其中以BP神经网络的一阶递进效果最好，其次是支持向量机模型，最后是GM(1,1)模型。

3.2 二阶递进预测

为进一步提高预测精度在采用组合预测的方法，对一阶递进预测结果进行二阶递进预测。在组合预测中，采用定权和非定权两种组合预测模式。定权主要包含了特尔菲法和变异系数法，其组合预测结果如表2所示。

表2 二阶定权组合预测

通过定权组合预测，预测精度较一阶递进预测模型的精度均有一定程度的提高，特尔斐法的最大相对预测误差为2.78%，最小相对误差为0.61%；而变异系数法的最大相对误差为3.04%，最小相对误差为0.87%。对比得出，特尔斐法的组合预测效果要优于变异系数法。

同时，非定权主要包含了误差倒数法和BP神经网络，组合的预测结果如表3所示。

表3 二阶非定权组合预测

由表3分析可知，非定权组合预测的预测精度较一阶递进预测模型的结果也具有一定程度的提高，误差倒数法的最大相对预测误差为2.81%，最小相对误差为0.27%；而BP神经网络的最大相对误差为2.66%，最小相对误差为0.45%。

同时，采用相对预测误差的期望及方差对二阶递进预测模型的预测效果进行评价，结果见表4。

表4 二阶递进预测模型结果对比

由表4对比二阶递进组合预测的结果可知，在预测精度方面，递进预测模型均高于传统的递进组合预测模型，且非定权组合预测较定权组合预测也具有更高的预测精度，其中以BP神经网络的组合预测模型精度最高；在预测稳定性方面，递进预测模型较传统的组合预测模型也具有更高的稳定性。综合对比，本文在二阶递进预测结果中，可选择BP神经网络组合预测的结果作为三阶递进预测的数据基础，进而探讨三阶递进预测的效果。

3.3 三阶递进预测

再采用马尔可夫链(MC)理论建立三阶递进的误差修正模型，对二阶递进预测中的最优预测结果进行误差修正，结果如表5所示。

表5 三阶递进预测结果

由表5可知，通过三阶递进的误差修正，进一步提高了本文的预测精度。其中，传统MC误差修正预测的相对误差的期望值为1.25%，方差为0.28，而三阶递进MC误差修正预测的相对误差的期望值为0.76%，方差为0.13。对比可知，三阶递进预测不仅进一步提高了预测精度，也提高了预测结果的稳定性，且本文的预测结果均优于传统预测的结果，也证明了本文预测模型的有效性。

3.4 预测结果的对比分析

为综合分析本文预测模型的适用性和可行性，采用预测误差的平方和为指标，进一步评价不同阶段及不同预测模型的效果。并考虑到一阶、二阶递进预测过程中，预测结果具有多样性，且不同预测节点在不同阶段的预测结果也具有差异，因此进一步采用平均误差平方和作为评价指标，结果如表6所示。

表6 不同阶段预测结果对比

对比不同阶段的预测结果，得出通过各阶段的不断递进，预测精度都有了提高，验证了递进预测思路的有效性和可行性；同时，预测模型较传统的预测模型，也具有更好的预测精度。综合得出，多阶段递进式预测模型及思路具有可行性和有效性，为基坑的变形预测提供了一种较好的思路。

4 结 论

(1) 通过一阶递进预测，得出传统预测模型具有一定的不足;通过对参数的优化，能很好的提高预测精度，且一阶递进预测模型预测结果的相对误差多集中在2%～3%之间。

(2) 通过二阶递进预测，得出本文采用的二阶递进组合预测模型均一定程度上提高的预测精度及稳定性，且非定权组合预测的结果优于定权组合预测的结果，并以BP神经网络的组合预测效果最好。

(3) 通过三阶递进预测，得出本文建立的MC误差修正模型具有其有效性，进一步提高了预测精度及其稳定性。

(4) 对比不同阶段的预测结果，得出通过各阶段的不断递进，预测精度及稳定性都有了提高，验证了本文递进预测思路的有效性和可行性。

[1] 杨爱婷,高正夏,卞志兵,等. 基于时间序列ACO-BP神经网络在基坑变形预测中的应用研究[J]. 路基工程,2015,(2):58-62.

[2] 曹 净,丁文云,赵党书,等. 基于LSSVM-ARMA模型的基坑变形时间序列预测[J]. 岩土力学,2014,35(增2):579-586.

[3] 李 莉,陈鹏宇,段新胜. 基坑变形预测的灰色二次优化模型[J]. 辽宁工程技术大学学报(自然科学版),2010,29(5):926-929.

[4] 石星照,顾胜宇. 基于灰关联定权组合模型的基坑变形预测分析[J]. 工程质量,2016,34(1):38-44.

[5] 钱大林,张志伟,靳璐岩. 基于神经网络的组合模型在基坑沉降预测中的应用研究[J]. 现代测绘,2014, 37(5):8-11.

[6] 任丽芳,袁宝远,王 江. 应用灰色神经网络组合模型预测深基坑变形[J]. 路基工程,2007(5):22-24.

[7] 杨 青,吉文来,石星照,等. 基于蚁群-BP神经网络的基坑变形预测[J]. 现代测绘,2012,35(6):13-14+27.

[8] 刘文生,吴作启,崔铁军,等. 基于改进灰色系统的深基坑变形预测方法研究[J]. 中国安全生产科学技术,2014,10(11):21-26.

[9] 刘淑官,黄声享,徐北海,等. 基于无偏灰色马尔科夫链的基坑沉降预测研究[J]. 测绘地理信息,2015, 40(4):10-13.

[10]黄传胜,张家生. 深基坑开挖变形的灰色马尔科夫链预测方法[J]. 铁道科学与工程学报,2011, 8(2):71-75.

(编辑：王 慰)

Application of Multi-stage Progressive Model to Predicting Foundation Pit Deformation

ZHOU Yong-sheng

(Shaanxi Railway Institute, Weinan 714000, China)

The aim of this research is to improve the precision of pit deformation prediction and enhance the stability of prediction results. Support vector machine, BP neural network and GM (1,1) are used as the basis of prediction model, and the corresponding first-order prediction models with parameters optimized are established. On this basis, the second-order combinatorial forecasting model of multiple fixed weight and non-fixed weight is established. In subsequence, on the basis of the Markov chain theory, the error correction model of three steps is established, and the progressive prediction of foundation pit deformation is realized. Results demonstrate that the prediction accuracy and stability are greatly improved by the progressive prediction of multiple stages, which verifies the validity and feasibility of the proposed method in this paper. The result is expected to provide a new idea for the prediction of foundation pit deformation.

foundation pit; progressive prediction model;support vector machines;BP neural network;GM(1,1); combinatorial forecasting; error correction

2016-05-08；

2016-06-17

周永胜(1977-)，男,甘肃天水人，讲师，硕士，主要从事铁道工程方面教学和研究工作，(电话)13572738156(电子信箱)18437224@qq.com。

10.11988/ckyyb.20160449

2017,34(8):47-51

TU753

A

1001-5485(2017)08-0047-05