福建省阔叶树多形地位(级)指数曲线模型研究

卓立新

(福建省林业调查规划院，福建 福州 350003)

福建省阔叶树多形地位(级)指数曲线模型研究

卓立新*

(福建省林业调查规划院，福建 福州 350003)

以福建省范围内收集到的1 907套阔叶树样木为建模数据，选择Korf生长方程，应用改进单纯形法，构建阔叶树多形地位(级)指数曲线模型。研究表明：所建立的阔叶树人工林、天然林多形地位(级)指数曲线模型误差较小、精度较高，可在林业生产活动中推广应用。

改进单纯形法；多形地位(级)指数；Korf生长方程

森林立地质量是影响林木产量的一大重要因素，不同立地条件有着不同的林木输出。科学预估森林生产潜力是森林经营活动顺利开展的一项重要基础工作。多形曲线模型是评定森林立地质量和预估各年龄林分平均高和优势高的有用工具。笔者以阔叶树为研究对象，选择Korf生长方程，应用改进单纯形法，构建多形地位(级)指数曲线模型，是一种低误差、高精度且简便实用的有效方法。

1 数据来源

在全省范围内收集阔叶树的样木(含解析木)、样地和标准地(统称样地)数据，样木共计1907套，样地共计665块(表1、表2)。

表1 样地主要林分因子分布范围

表2 样木主要测树因子分布范围

2 研究方法

2.1 模型原理

地位(级)指数曲线模型的实践意义在于预估各年龄的平均树高，该目标实现的前提条件是依据年龄和平均树高所确定的地位(级)指数准确。因此我们在所构造的平均树高和地位(级)指数均能写成显式表达式的多形地位(级)指数曲线模型的基础上，以平均树高和地位(级)指数两者的估测误差最小为目标函数[1-2]，采用改进单纯形法求解参数，建立简便、实用且满足精度要求的多形地位(级)曲线模型。

2.2 模型构造

选择Korf方程来描述平均树高生长过程：

H=a·e(-b/TC)

(1)

式中：H为平均树高，T为年龄，a、b、c为参数。

若林分T1、T2年对应的平均树高分别为H1、H2，消去(1)式中的参数b，得到差分方程：

H2=a·(H1/a)(T1/T2)C

(2)

参数a用来反映不同立地条件下林分的平均树高生长的极限，通常情况下，它与地位指数SI呈幂函数关系，即a=b1·SIb2。若T1=T0(基准年龄)，则H1=SI；若T2=T时，则H2=H，(2)式可转化为：

H=b1·SI·b2·[SI/(b1·SIb2)](T0/T)C

(3)

进一步整理得到用来反映不同立地条件下林分平均树高的生长过程的多形地位(级)指数曲线模型：

H=b1[1-(T0/T)C]·SI[b2+(1-b2)·(T0/T)C]

(4)

再进一步整理，得到多形地位(级)指数的显示表达式：

(5)

(5)式直接反映多形地位(级)指数与林分年龄和平均树高的函数关系，无须迭代计算，应用简便。

2.3 参数求解

研究构建地位(级)指数曲线模型的最终目标是利用所建立的曲线模型预估林分的平均树高。要保证达到最终目标且有现实意义，必须保证所确定的地位(级)指数准确无误。所以，以往求解多形地位(级)指数曲线模型参数所用的目标函数已不合适，现改进为既要保证平均树高估测误差绝对值最小，又要保证地位(级)指数的估测误差绝对值最小，即：

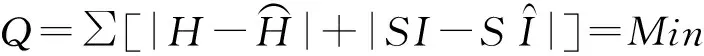
(6)

本次求解参数采用改进单纯形法[3-4]。

3 结果分析

阔叶树基准年龄取20 a，构建阔叶树地位(级)指数曲线模型(表3)，编制地位(级)指数(表4、表5)。

从地位指数统计指标分析阔叶树人工林、天然林地位(级)指数曲线模型的树高平均绝对误差<0.55 m，平均相对误差<5.5%，平均系统误差分别在-2%、1%左右，相关指数>0.80；拟合效果较好。从树高指数统计指标分析：阔叶树人工林、天然林地位(级)指数曲线模型的树高平均绝对误差<0.55 m，平均相对误差<5.5%，平均系统误差分别在3%、-1%左右，相关指数>0.95；拟合效果较好。

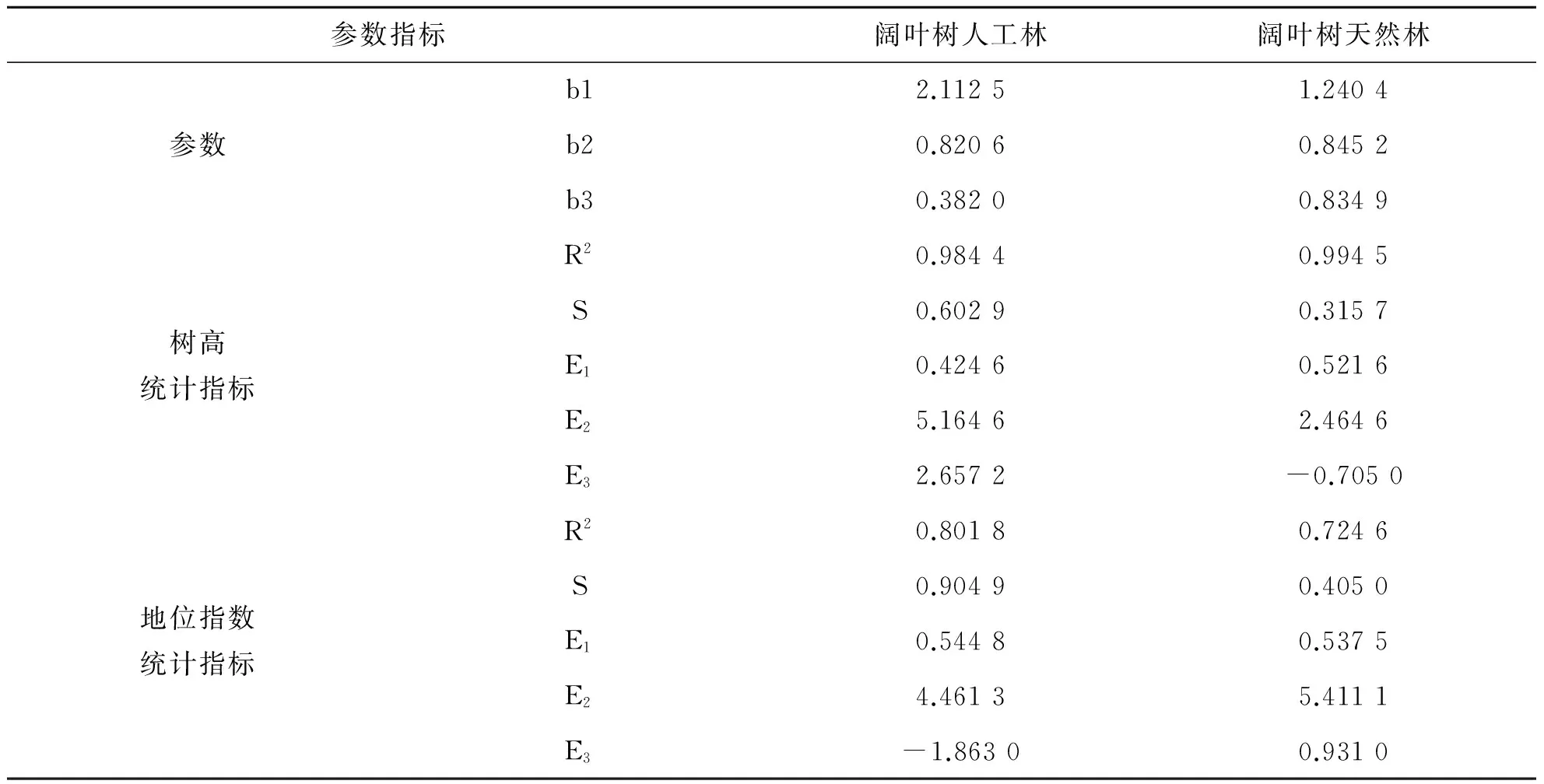
表3 阔叶树地位(级)指数曲线模型参数

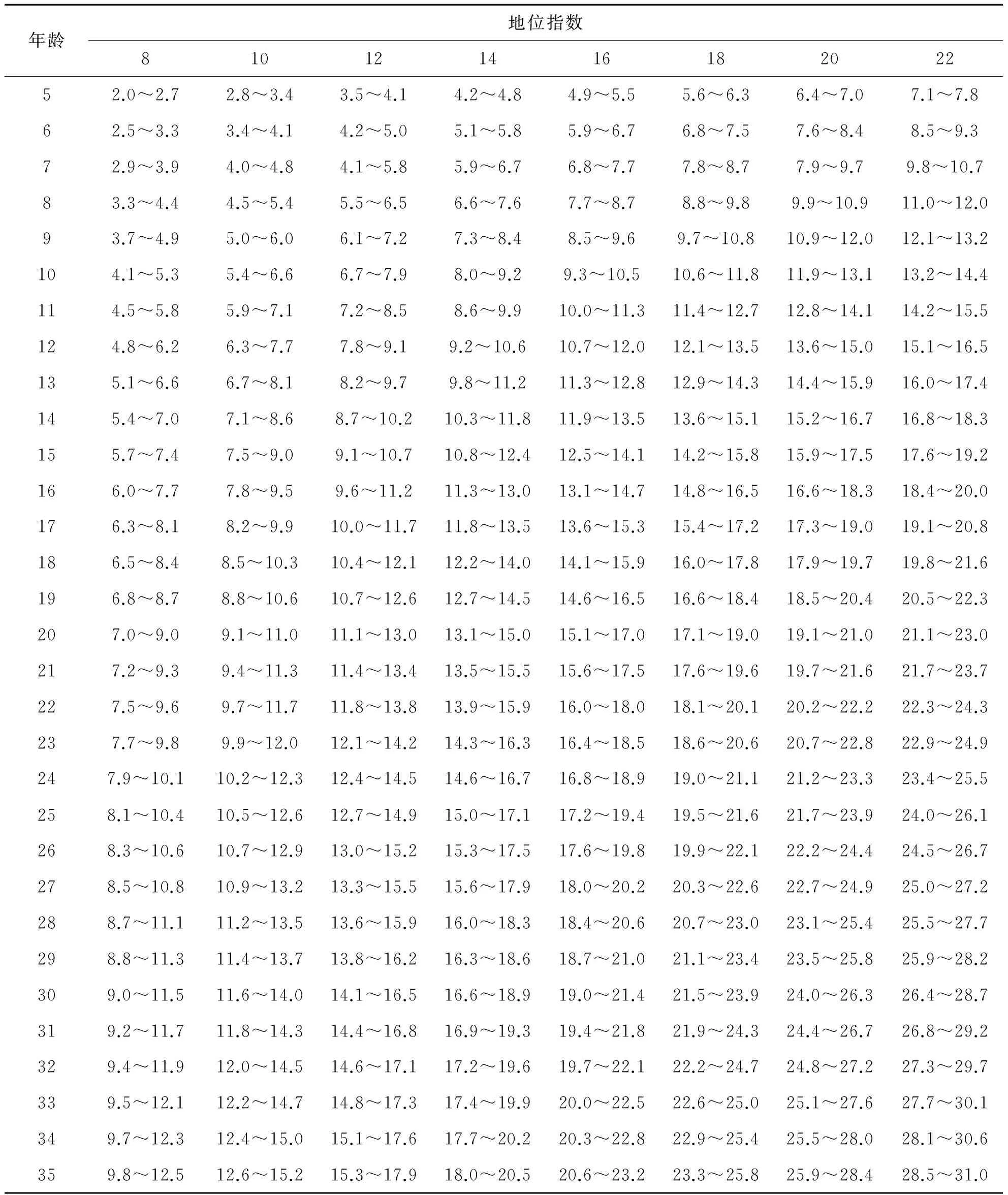
表4 阔叶树人工林地位指数

4 结论和讨论

建立的多形地位(级)指数模型能直接用年龄和平均树高的函数关系式表达，且以平均树高和地位(级)指数两者的估测误差最小为目标函数，所建立的模型误差小、精度高。

采用改进单纯形法求解参数，能避免异常数据对模型的影响，提高模型参数的稳定性，可作为建立简便、实用且满足精度要求的多形地位(级)曲线模型的一种新的技术方法。

本次编制的地位(级)指数表时，阔叶树基准年龄取20年，还值得商榷，所编的地位(级)指数表，仅是初步结果，实际使用精度需作进一步的检验。

表5 阔叶树天然林地位指数

续表五

年龄8101214161820224010.6～13.413.5～16.116.2～18.818.9～21.521.6～24.224.3～26.826.9～29.429.5～32.04110.7～13.513.6～16.316.4～19.019.1～21.721.8～24.424.5～27.127.2～29.729.8～32.34210.8～13.613.7～16.416.5～19.219.3～21.922.0～24.624.7～27.327.4～30.030.1～32.64310.9～13.813.9～16.616.7～19.419.5～22.122.2～24.824.9～27.527.6～30.230.3～32.94411.0～13.914.0～16.716.8～19.519.6～22.322.4～25.025.1～27.727.8～30.430.5～33.14511.1～14.014.1～16.917.0～19.719.8～22.522.6～25.225.3～28.028.1～30.730.8～33.34611.2～14.114.2～17.017.1～19.819.9～22.622.7～25.425.5～28.228.3～30.931.0～33.64711.3～14.214.3～17.117.2～20.020.1～22.822.9～25.625.7～28.428.5～31.131.2～33.84811.4～14.414.5～17.317.4～20.120.2～23.023.1～25.825.9～28.528.6～31.331.4～34.04911.5～14.514.6～17.417.5～20.320.4～23.123.2～25.926.0～28.728.8～31.531.6～34.25011.6～14.614.7～17.517.6～20.420.5～23.323.4～26.126.2～28.929.0～31.731.8～34.4

[1] 陈绍玲．马尾松人工林多形地位指数曲线模型的建模方法 [J]．中南林业科技大学学报，2007，28(2)：125-128.

[2] 施恭明．马尾松人工林货币收获表的研究 [J]．林业勘察设计，2011(1)：4-9.

[3] 江希钿，罗明永，黄以平．地位指数多形曲线的优化及与同形曲线的比较 [J]．福建林学院学报，1996，16(2)：130-134.

[4] 林思祖，林开敏，洪伟．改进单纯形法拟合多形地位指数曲线模型的研究 [J]．福建林学院学报，1997，17(2)：140-143.

[5] 骆期邦，曾伟生，贺东北．林业数表模型理论、方法与实践 [M]．长沙：湖南科学技术出版社，2001.

卓立新(1964-)，男，福建连江人，林业工程师，主要从事森林经理、规划设计、森林资源监测等领域研究，(E-mail)245936307@qq.com。

文献标识码：A 文章编号：1004-2180(2017)02-0029-05