“用样本的频率分布估计总体分布”教学设计及反思

执教者：哈尔滨市第三中学郜新利指导者：哈尔滨市第三中学 梁艳娟

“用样本的频率分布估计总体分布”教学设计及反思

执教者：哈尔滨市第三中学郜新利
指导者：哈尔滨市第三中学 梁艳娟

教学目标：

1.知识和技能

（1）能列出频率分布表，能画出频率分布的条形图、直方图；

（2）会用样本频率分布去估计总体分布.

2.过程与方法

（1）体会分布的意义和作用；

（2）初步体会样本频率分布和数字特征的随机性.

3.情感态度与价值观

（1）体会用样本估计总体的思想；

（2）通过研究具体问题，体会“探究学习”在学习过程中的作用，使学生体验成功，增强学习数学的自信心.

重难点分析：

重点：列出频率分布表，绘制频率直方图，用样本频率分布去估计总体分布.

难点：统计思维的建立.

教学环节：

复习回顾：某火柴厂生产壁炉火柴、书式火柴、酒店火柴、广告火柴等系列产品的技术已经成熟，现在要对一批新产品宾馆火柴的质量进行检验，应该如何操作？

师生互动：教师提问，学生思考讨论.

设计意图：使学生认识到用样本估计总体的必要性.

本节课我们来共同解决一个问题：

某城市为节约用水，计划确定一个居民月用水量标准a，超出a的部分按议价收费.如果希望大部分居民日常生活不受影响，怎样确定这个标准？需要做哪些工作？

现有100位居民的月均用水量（单位：t）

3.12.52.02.01.51.01.61.81.91.6

3.42.62.22.21.51.20.20.40.30.4

3.22.72.32.11.61.23.71.50.53.8

3.32.82.32.21.71.23.61.70.64.1

3.22.92.42.31.81.33.51.90.84.3

3.02.92.42.41.91.41.41.80.72.0

2.52.82.32.31.81.31.31.60.92.3

2.62.72.42.11.71.31.21.50.52.4

2.52.62.32.11.61.41.01.70.82.4

2.82.52.22.01.51.01.21.80.62.2

从表中只能看出：最小值是0.2t，最大值是4.3t，其他的在0.2—4.3t之间.

师生互动：教师用幻灯片演示，学生观察数据特点，并考虑分析数据的基本方法.

设计意图：用样本数据分布特征估计总体数据分布.

分析数据的基本方法：

1.表（频率分布表）2.图（频率分布直方图）

画频率分布直方图的一般步骤：

1.求极差：4.3-0.2=4.1，该样本数据的变化范围是0.2—4.3t.

2.定组距：当样本容量不超过100时，常分成5—12组.取组距为0.5t，则分组数=4.1÷0.5=8.2.因为组数必须取整，因此将数据分为9组.

3.适当分组：为将最小值包含在第一组内，常将第一组区间的左端点适当缩小，[0，0.5），[0.5，1），[1，1.5），…，（4，4.5]

4.列频率分布表：如下表.

?

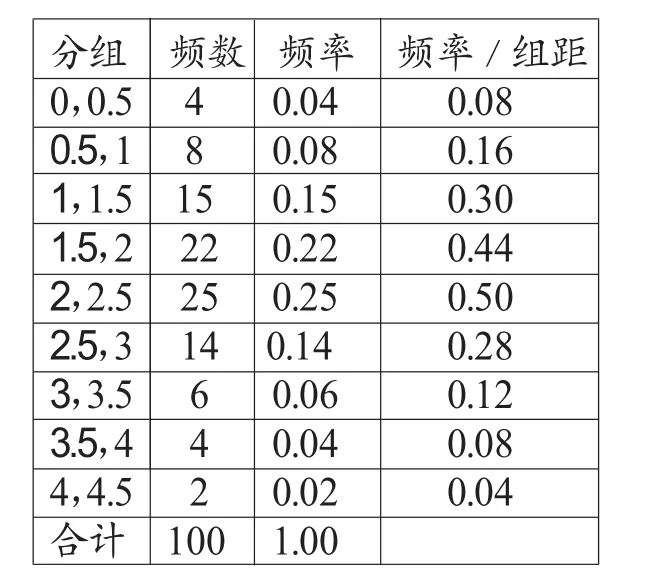
5.画频率分布直方图：如下图.

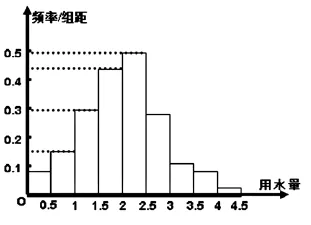
师生互动：教师引导，学生讨论，动手操作，共同解决问题.

设计意图：使学生形成规范的画频率分布直方图的步骤.

师：每个小矩形的面积代表什么？

生：各组频率.

师：所有小矩形面积的和是多少？

生：每个小矩形的面积代表频率，面积和为1.

师：频率分布直方图显示了样本数据分布的总体趋势.图中最高的小矩形说明什么？

生：说明月均用水量在[2，2.5）内的居民最多.

师：大部分居民的月均用水量都集中在什么区间？

生：在[1，3）之间.

师：居民的月均用水量的分布呈“山峰”状，而且是“单峰”的.另外还有一定的对称性.

师：如果当地政府希望使85%以上的居民每月的用水量不超出标准，根据频率分布表，该如何制定月用水量标准？

生：居民月用水量标准应定为3t.

师：3t的标准一定能保证85%以上的居民每月的用水量不超出标准吗？

生：不能.频率分布直方图具有随机性.

师：指导学生用图形计算器画频率分布直方图.

师：怎样减小误差？

生：思考并探讨.

师：频率分布直方图有没有不足之处？

生：频率分布直方图丢失原始数据.

例1：从一种零件中抽取了80件，尺寸数据表示如下（单位：cm）：

362.51×1 362.62×2 362.72×2 362.83×3

362.93×3 363.03×3 363.15×5 363.26×6

363.38×8 363.49×9 363.59×9 363.67×7

363.76×6 363.84×4 363.93×3 364.03×3

364.12×2 364.22×2 364.31×1 364.41×1

画出频率分布直方图.

总结频率分布直方图的特征：

1.每个矩形面积表示该组频率.

2.所有矩形面积和为1.

3.若样本容量为n，分组应在1+3.3lgn.

4.频率分布直方图形状与分组数有关.

5.有随机性.

6.丢失原始数据.

设计意图：让学生学会用图形计算器辅助学习.使学生体会分组变化对频率分布直方图形状和频率分布表中数据的影响.体会频率分布直方图的随机性.

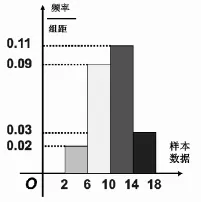
练习1：右图是容量为100的样本的频率分布直方图，试根据图中的数据填空：

（1）样本数据落在范围[6，10）内的频率为_____；

（2）样本数据落在范围[10，14）内的频数为_____；

（3）总体在范围[2，6）内的概率约为.

设计意图：让学生体会频率分布直方图的随机性和丢失原始数据的特点.

小结：

1.掌握了绘制频率分布直方图的步骤；

2.掌握了频率分布直方图的特征；

3.学习用样本估计总体的思想.

作业：教材57页练习1.

总结：

1.本节课三次使用了图形计算器，一是新知学习中的作图；二是新知学习中复杂数据的计算；三是课堂练习.

2.本节课涉及的知识点多，学生动手多，学生参与多.有了图形计算器的帮助，所有学生都能投入到学习过程中，教师提出的每个问题都在不同程度的学生那里得到了解决，实现了全员参与.本节课教师讲解少.教师的作用重在提出问题，引导学生逐步深入地进行学习.

3.本节课的教学效果，用学生的话说：“知识挺简单的，考试时要是能用计算器就好了.”

教学反思：

当时代的脚步推动我们不断向前进，当新课程的推行促使我们改进教学理念，当学生的成长要求我们推陈出新的时候，我们已经没有任何理由拒绝任何新的事物.新事物并不可怕，关键是我们能否恰当吸收与运用.图形计算器本身不是新事物，但新课程与图形计算器的结合并有效运用仍然是新事物.本节课特点在于探索现代信息技术在数学教学中的应用，发挥图形计算器处理大量数据的优势，让学生的学习更高效，也让学生体会数学的应用价值.

在学生使用图形计算器绘制频率分布直方图的环节，针对不同的分组情况，如选出有代表性的几名学生的不同分组方法，画出不同的频率分布直方图可以使学生体会到不同的组距对作图的影响，更有利于学生体会数据处理的灵活性及科学性.若将题目中的原始数据改为200个，再让学生体会不同的分组对作图的影响，课堂效果会更好.

课程中所蕴含的数学的过程学习，对实际问题的处理，数学能力的培养，都要求学生亲身参与.本节课的教学可以说为我们提供了一个参考的范例，更好地促进了广大一线教师对现代信息技术与数学教学相结合的探索.

编辑/王一鸣E-mail：51213148@qq.com