轮廓法测试残余应力中的数据处理
2017-08-31谢国贞吴运新刘瑶琼1
谢国贞 吴运新 龚 海 李 晨 刘瑶琼1, 姬 浩 张 伟
1. 中南大学机电工程学院,长沙,4100832. 高性能复杂制造国家重点实验室,长沙,4100833.有色金属先进结构材料与制造协同创新中心,长沙,4100834. 中国航空工业集团公司第一飞机设计研究院,西安,710000
轮廓法测试残余应力中的数据处理
谢国贞1,2,3吴运新1,2,3龚 海1,2,3李 晨4刘瑶琼1,4姬 浩4张 伟4
1. 中南大学机电工程学院,长沙,4100832. 高性能复杂制造国家重点实验室,长沙,4100833.有色金属先进结构材料与制造协同创新中心,长沙,4100834. 中国航空工业集团公司第一飞机设计研究院,西安,710000
使用轮廓法测量铝合金T形构件淬火残余应力,重点研究了测量误差的数据处理。采用包络处理、左右轮廓平均、Gauss混合模型拟合以及节点插值处理后,得到最终轮廓值,并将其作为边界条件反向加载到应力重构有限元模型中,得到待测面应力场。使用X射线衍射法对待测面边界处应力进行修正。将测量结果和有限元模拟淬火结果进行对比,利用统计学方法分析对比结果。结果表明:轮廓法和X射线衍射法结合可以很准确地描述T形构件淬火残余应力场。T形构件淬火残余应力最大拉应力出现在筋条和腹板交界处,靠近腹板一侧。
轮廓法;数据处理;铝合金;T形构件;残余应力
0 引言
7050高强铝合金具有强度高、断裂韧性好、抗腐蚀能力强和淬透性好等优点,是航空航天领域中被广泛应用的材料[1-2]。对可热处理强化的铝合金进行淬火处理是为了得到过饱和α固溶体,为其后时效强化、提高强度和硬度创造必要条件[3],但是在材料淬火急冷的过程中,材料内外温度差作用会引入大量 “外压内拉”的淬火应力[4]。较大的淬火残余应力会造成后期明显的加工变形,影响加工精度,尤其是在航空航天工业中,材料的去除率高达70%~95%。同时,较大的残余应力会降低零件疲劳寿命,造成安全隐患。由此,对淬火残余应力进行量化和分析有着重大意义。
目前,残余应力的测试方法分为破坏法和无损检测两大种类:破坏法又分为盲孔法、轮廓法、层削法和裂纹柔度法等;无损检测又分为X射线衍射法和中子衍射法等[5]。盲孔法已经有比较成熟的应用,但其检测结果为钻孔深度应力平均值。廖凯等[6]在铝合金厚板残余应力测试中,对裂纹柔度法和层削法作了深入研究。PRIME[7]首次提出了轮廓法测试原理,并利用轮廓法测试HSLA-100钢板的淬火残余应力[8]。TURSKI等[9]利用轮廓法测试3161不锈钢焊板的残余应力。ZHANG等[10]利用轮廓法测试VPPA焊接残余应力。无损检测中,X射线衍射法具有较高的测量精度,但是受限于X射线的穿透能力,该方法只能测量材料表面残余应力[11];相对而言,中子有较强的穿透能力,可实现毫米级别的探测,但设备昂贵稀少且国内尚在设备研制阶段。在轮廓法测试中,存在以下问题:线切割丝振荡,走丝不均;在三坐标机上测量轮廓时,工件不能绝对放置水平,导致测量结果是叠加在一个原始倾斜平面上的。由此,需采用合适的算法来处理以上误差,以达到准确测量截面应力的目的[12]。
本文采用轮廓法测试典型T形7050铝合金构件淬火残余应力,采用包络处理、左右轮廓数据平均处理、混合高斯模型拟合、有限元节点插值算法提高测量精度。
1 轮廓法原理
轮廓法测试材料内部残余应力的原理是在Bueckner叠加原理之上衍生出来的[7]。基本原理如图1所示。
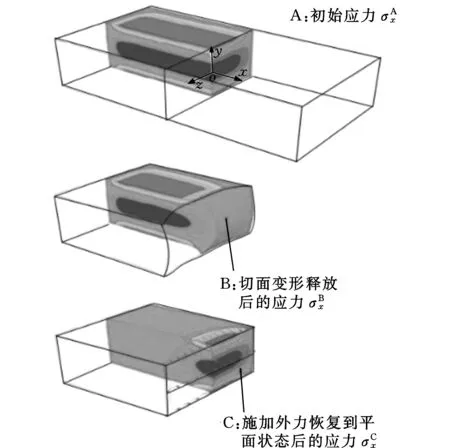
图1 轮廓法基本原理Fig.1 Fundamental principle of contour method
A中待测oxy平面上的初始应力为σA(x,y,z),B中平面oxy切割变形后截面上的应力为σB(x,y,z),C中对无应力试块施加外力使得切割变形后的曲面恢复到切割前的平面状态后的应力为σC(x,y,z)。根据Bueckner叠加原理,有
σA(x,y,z)=σB(x,y,z)+σC(x,y,z)
(1)

(2)
测得oxy截面上x方向变形量,将此变形量反向加载到无应力有限元模型中,即可得到截面应力。
2 实验
2.1 实验材料
选取某铝厂生产的7050-T7451铝合金厚板,加工成T形构件,试件长度为500 mm。具体截面尺寸如图2所示。
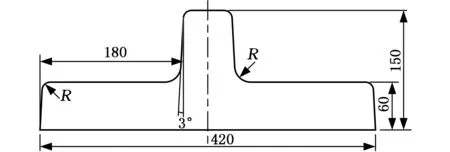
图2 构件截面尺寸Fig.2 Section size of the component
2.2 实验步骤
2.2.1 淬火
使用固溶加热炉JTRX20-6在2.5 h内将构件加热到475 ℃,并在475 ℃下保温2 h。然后将构件在15 s内转移到足够大的淬火池中,淬火池水温为20 ℃,入水方式为侧面入水。
2.2.2 试件切割
线切割的表面质量是影响轮廓法测试结果最大的因素。实验使用苏州三光DK7625P型慢走丝线切割机。走丝速度为1 mm/min,切割丝使用0.2 mm铜丝。为保证平面切割假设条件,实验中在切割面两边对称夹紧,并且不能引入装夹应力。
2.2.3 表面轮廓测量
使用MQ8106接触式三坐标测量仪。误差为0.1 μm,切割面上测点间距为5 mm×5 mm。
2.2.4 应力重构分析
将处理后的变形轮廓数据取反作为位移边界条件加载到无初始应力线弹性有限元模型中,得到的切割面正应力即所测截面正应力。使用无初始应力模型理由如下:①切割后试块残余应力场是未知的;②材料切割后,表层法向应力已释放为0,产生的法向变形量很小,施加在有限元模型后只会在截面表层产生影响[7]。理论上,所加载轮廓数据应为截面上所有测点相对于原始切割面的位移。由于实际中无法做到绝对零宽度切割,并且通过力和力矩平衡计算的原始切割面存在误差,故在应力重构分析中,约束模型x、y方向的移动自由度以及z方向的转动自由度,使得有限元模型通过力和力矩自适应自动寻找原始切割面,并能限制模型刚性位移。有限元约束条件如图3所示。
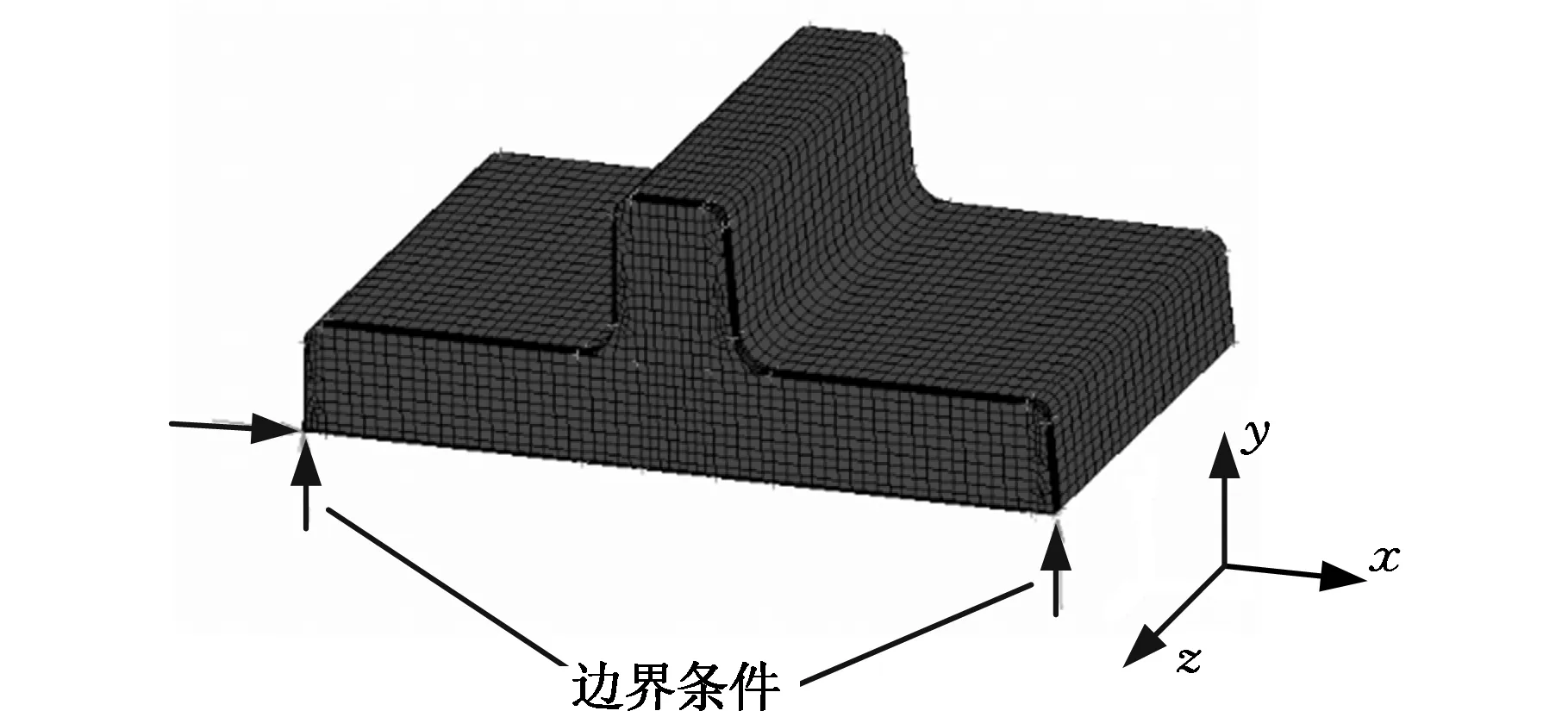
图3 应力重构有限元模型Fig.3 Finite element model of residual stress reconstruction
2.3 轮廓数据处理
2.3.1 轮廓包络处理
使用三坐标仪测量轮廓时,试件无法保持绝对水平,导致测量轮廓结果是叠加在一个原始倾斜面上的。使用轮廓包络处理可以消除这一误差。包络处理的基本原理是寻找距离最小的相互平行的两平面,使得所有的测点都被包络到两平行面之间。设定平行平面法向量为N(A,B,C),点(xi,yi,zi) 到面的距离方程为
(3)
包络面间距方程:
D=max(di)-min(di)
(4)

(5)
2.3.2 左右轮廓值平均
轮廓法假设线切割时,切割丝轨迹为绝对直线,即变形前的切割面是绝对平面,但是在实验中,平面假设是完全做不到的,切割丝存在横向振动或产生弧形走丝轨迹,这对单侧变形轮廓会有很大的影响,通过左右轮廓值平均可以消除这种误差。如图4所示,在边缘区域,左侧轮廓值明显大于右侧轮廓值。切割轨迹在中点处向左侧偏,切割平面在左侧形成了凹形,而在右侧形成了凸形,轮廓数据是在此基础上测量出来的。通过左右轮廓值平均可以消除这部分误差。

图4 左右轮廓值平均Fig.4 Average of left and right contour
2.3.3 轮廓拟合
当切割截面厚度发生突变时,放电电流也会发生突变。在突变位置会发生轮廓畸形,出现小“台阶”。这种误差无法通过左右轮廓平均处理来消除。此时,可以通过轮廓光滑拟合来消减这部分误差。轮廓拟合还可以消除部分测量误差。Prime[8]使用二维Fourier级数进行拟合;Prime[13]还使用过基于最小二乘法的B样条拟合;文献[14]则采用Sigmoid函数进行拟合。本文采用高斯混合模型拟合:
(6)
当N分别为4、6、8时,拟合结果如图5和表1所示。
N=4时的拟合效果明显比N=6、N=8时的拟合效果差,N=6、N=8两种情况只有很细微的差别。N=6、N=8时的残差平方和(SSE)已在10-4数量级,而且拟合优度已接近1,此时N再增大,对拟合优度已没有意义,反而会使测量误差的过滤效果变差。当拟合的数据点较少时,求解系数ai、bi、ci(i=1,2,…,N)无法得到唯一解,此时减小N,即可得到拟合结果。同时,数据点的减少也可减小SSE,提高拟合优度,不必担心N的适当减小对拟合效果的影响。使用高斯混合模型拟合轮廓数据有足够的精度,经高斯拟合后的轮廓如图6所示。

图6 高斯拟合后的轮廓Fig.6 Contour of the Gaussian fitting
2.3.4 有限元节点插值
为得到应力重构有限元模型截面节点的轮廓数据,本文采用MATLAB中的V4算法,将拟合后的轮廓数据在节点坐标上进行插值,得到最终轮廓数据。
2.4 应力分析
根据切割后一半的试件尺寸,在MSC.Marc中建立应力重构有限元模型,使用六面体八节点单元,泊松比为0.33,弹性模量为71 GPa。单元网格大小以及类型对有限元计算精度有很大影响。如图7所示,采用三种不同大小单元进行计算,取图8中L2路径的应力进行对比。发现当单元大小为2 mm×2 mm×2 mm时,计算结果和1 mm×1 mm×1 mm单元模型已经很相近,此时再减小单元尺寸已无意义,因此,在计算中选取2 mm×2 mm×2 mm六面体八节点单元。

图7 不同单元尺寸对计算结果影响Fig.7 The influence of different element size on the calculations

图8 轮廓法与淬火仿真结果对比Fig.8 Comparison of contour method and simulation results
根据切割前试件尺寸,在MSC.Marc中建立全尺寸有限元模型,模型网格大小、类型、材料参数与应力重构有限元模型一致,进行淬火仿真并提取所测截面正应力。
如图8所示,选取截面上5条路径,对比淬火仿真和轮廓法测试结果。5条路径应力对比结果如图9所示。
在使用三坐标仪时,边界区域轮廓无法测得。其轮廓数据是外插值所得,应力误差大。实验中,以X射线衍射方法对此区域进行应力补偿。在试件线切割前,使用加拿大Proto公司生产的iXRD便携式残余应力分析仪测量L5路径上垂直于切割面方向的应力。
从图9a~图9d可以看出,T形构件淬火残余应力呈现“外压内拉”的分布规律。轮廓法测得应力同有限元计算结果很接近,变化趋势相同。在相同淬火温度和淬火介质下,淬火残余应力的最大值和毕渥数Bi有关[8]:
Bi=hl/k
(7)
式中,h为表面传热系数;l为特征长度(厚度为2a的板特征长度为a,半径为R的球特征长度为R);k为固体导热系数。

(a)沿L1路径的应力

(b)沿L2路径的应力

(c)沿L3路径的应力

(d)沿L4路径的应力
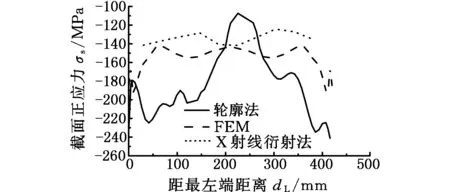
(e)沿L5路径的应力图9 5条路径应力对比Fig.9 Comparison of residual stress on 5 paths
由于筋条的存在,腹板区(L1、L3区)特征长度比筋条区(L2路径中下部)特征长度小,其残余应力最大值比筋条部位残余应力最大值小。腹板区域沿L3路径心部最大应力为155.8 MPa,边缘最大压应力为-175.6 MPa,轮廓法测量结果同有限元计算结果相近;筋条区域沿L2路径上,轮廓法测得最大拉应力为231 MPa,有限元计算结果为拉应力201 MPa,应力差别稍大。同时,T形构件淬火残余应力最大值出现在筋条和腹板交界线偏下处,实验中表征为L2路径应力不对称,最大值出现在靠近底面一侧;沿L4路径,应力分布左右对称,由于边界效应的影响,在两端由拉应力向压应力快速过渡。
沿L5路径,轮廓法所测得应力和有限元计算结果有大体相同的变化趋势,但应力值有较大差别。X射线衍射法和有限元计算结果比较接近。在中心区域,X射线测试结果在-128.44 MPa到-141.68 MPa之间浮动。定义测量相对偏差:
(8)

(9)


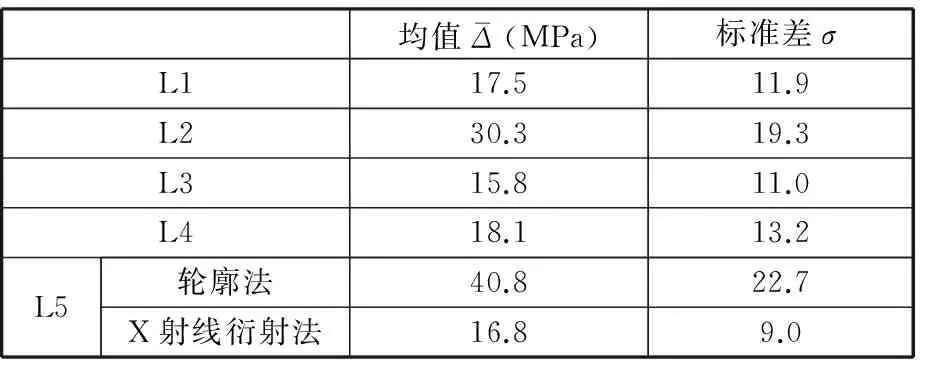
表2 均值、方差对比

正因为轮廓法对材料内部残余应力场有很好的测量效果,对于表面的应力测量误差较大,X射线衍射法能很好地描述表面应力水平,因此,将轮廓法和X射线衍射法相结合,可以准确描述测量截面的残余应力。
3 结论
(1)在测量表面轮廓时,包络处理可以消除工件不水平而造成的误差;使用截面左右两侧轮廓平均的方法来消除切割线走丝不直的误差;混合高斯模型可以很好地拟合轮廓数据,减小测量误差。
(2)T形构件在某一截面上淬火残余应力最大值出现在筋条与腹板交界线处,偏向于腹板的一边。
(3)轮廓法测量材料内部残余应力准确度较高。X射线衍射法所得表面残余应力有较高的可信度。可结合轮廓法和X射线衍射方法来测量材料某截面残余应力场。
[1] ZHONG Jue. Progress in the Basic Research of Improving Aluminum Materials Quality [J]. Light Alloy Fabrication Technology,2002,30(5):1-10.
[2] 杨守杰, 杨霞. 高强度铝合金的研究进展[J]. 粉末冶金工业,2010,20(5):47-52. YANG Shoujie,YANG Xia. Progress in High-strength Aluminum Alloy Research[J].Powder Metallurgy Industry,2010,20(5):47-52.
[3] 李兴杰.热处理对ADC12铝合金组织和性能的影响[D]. 沈阳:东北大学,2006. LI Xingjie. Effect of Heat Treatment on Microstructure and Properties of ADC12 Al Alloy[D].Shenyang:Northeastern University,2006.
[4] 曹明慧.7050铝合金典型构件淬火残余应力建模分析与实验研究[D].长沙:中南大学,2015. CAO Minghui. Modeling Analysis and Experimental Research on Quenching Residual Stress of 7050 Aluminum Alloy Typical Component[D].Changsha: Central South University,2015.
[5] 龚海. 铝合金厚板内应力演变规律及残余应力场评估模型研究[D].长沙:中南大学,2011. GONG Hai. Research on Evolution and Evaluation Model of Residual Stress in Aluminum Alloy Thick Plate[D]. Changsha: Central South University,2011.
[6] 廖凯, 吴运新, 龚海.基于积分法的铝合金厚板深度残余应力分析[J].中南大学学报(自然科学版),2010,41(1):179-183. LIAO Kai, WU Yunxin, GONG Hai. Analysis of Measuring Residual Stress Depth Profiling in Aluminum Alloy Thick Plate Using Integral Method [J]. Journal of Central South University (Science and Technology),2010,41(1):179-183.
[7] PRIME M B. Cross-sectional Mapping of Residual Stresses by Measuring the Surface Contour after a Cut [J]. Journal of Engineering Materials & Technology,2001,123(2):162-168.
[8] PRIME M B. Residual Stresses Measured in Quenched HSLA-100 Steel Plate [C]//Proceedings of the 2005 SEM Annual Conference and Exposition on Experimental and Applied Mechanics.Portland,2005: Paper Number 52.
[9] TURSKI M, EDWARDS L. Residual Stress Measurement of a 3161 Stainless Steel Bead-on-plate Specimen utilizing the Contour Method[J]. International Journal of Pressure Vessels & Piping,2009,86(1):126-131.
[10] ZHANG Y, GANGULY S, EDWARDS L, et al. Cross-sectional Mapping of Residual Stresses in a VPPA Weld Using the Contour Method [J]. Acta Materialia,2004,52(17):5225-5232.
[11] 张定铨,何家文. 材料中残余应力的X射线衍射分析和作用[M].西安:西安交通大学出版社,2000. ZHANG Dingquan, HE Jiawen. Residual Stress Analysis by X-ray Diffraction and Its Functions[M].Xi’an:Xi’an Jiaotong University Press,2000.
[12] 唐志涛, 刘战强, 艾兴. 高速铣削加工铝合金表面残余应力研究[J].中国机械工程,2008,19(6):699-703. TANG Zhitao, LIU Zhanqiang, AI Xing. Experimentation on the Superficial Residual Stresses Generated by High-speed Milling Aluminum Alloy[J]. China Mechanical Engineering,2008,19(6):699-703.
[13] PRIME M B. Laser Surface-contouring and Spline Data-smoothing for Residual Stress Measurement [J]. Experimental Mechanics,2004,44(2):176-184.
[14] 刘川, 庄栋. 基于轮廓法测试焊接件内部残余应力[J]. 机械工程学报,2012,48(8):54-59. LIU Chuan, ZHUANG Dong. Internal Welding Residual Stress Measurement Based on Contour Method[J]. Journal of Mechanical Engineering,2012,48(8):54-59.
(编辑 陈 勇)
Data Processing in Residual Stress Measurements Using Contour Method
XIE Guozhen1,2,3WU Yunxin1,2,3GONG Hai1, 2,3LI Chen4LIU Yaoqiong1,4JI Hao4ZHANG Wei4
1.College of Mechanical and Electrical Engineering, Central South University, Changsha,410083 2.State Key Laboratory of High Performance Complex Manufacturing,Changsha, 410083 3.Nonferrous Metal Oriented Advanced Structural Materials and Manufacturing Cooperative Innovation Center, Changsha,410083 4.AVIC the First Aircraft Institute, Xi’an,710000
The quenched residual stresses of T-shaped aluminum alloy were tested using the contour method, and the data processing of measurement errors was focused. The final contours were calculated by envelop processing, contour averaging, Gauss mixed model fitting and node interpolation, and then were reversed and loaded to the stress reconstruction FEM model as boundary conditions. Then the mapping of residual stresses along the cross section to be measured were obtained. The stresses at the edge were modified using X-ray diffraction method. The comparisons of measured results with quenching FEM results were analyzed via statistical methods. The results indicate that the quenched residual stress fields may be described accurately by combining contour method and X-ray diffraction method. The maximum tensile residual stress of the T-shaped specimen occurs at the junction of the rib and web, and close to the web.
contour method; data processing; aluminum alloy; T-shaped specimen; residual stress
2016-10-10
国家重点基础研究发展计划(973计划)资助项目(2012CB619505);国家自然科学基金资助项目(51327902,51405520);国家国际科技合作专项(2014DFA51250);高性能复杂制造国家重点实验室自主研究课题(ZZYJKT2016-02)
TG166.3
10.3969/j.issn.1004-132X.2017.15.003
谢国贞,男,1990年生。中南大学机电工程学院硕士研究生。E-mail: melaft@qq.com。吴运新,男,1963生。中南大学机电工程学院教授、博士研究生导师。 龚 海,男,1982年生。中南大学机电工程学院讲师。李 晨,女,1983年生。中国航空工业集团公司第一飞机设计研究院工程师。刘瑶琼,女,1986年生。中南大学机电工程学院博士研究生,中国航空工业集团公司第一飞机设计研究院工程师。姬 浩,男,1983年生。中国航空工业集团公司第一飞机设计研究院高级工程师。张 伟,男,1981年生。中国航空工业集团公司第一飞机设计研究院高级工程师。
