Phase estimation of phase shifts in two arms for an SU(1,1) interferometer with coherent and squeezed vacuum states∗
2017-08-30QianKunGong龚乾坤DongLi李栋ChunHuaYuan袁春华ZeYuQu区泽宇andWeiPingZhang张卫平
Qian-Kun Gong(龚乾坤),Dong Li(李栋),Chun-Hua Yuan(袁春华),4,†, Ze-Yu Qu(区泽宇),3,and Wei-Ping Zhang(张卫平)
1 Quantum Institute for Light and Atoms,School of Physics and Material Science,East China Normal University,Shanghai 200062,China
2 Department of Physics and Astronomy,Shanghai Jiao Tong University,Shanghai 200240,China
3 Department of Physics,Indiana University–Purdue University Indianapolis,Indianapolis 46202,USA
4 Collaborative Innovation Center of Extreme Optics,Shanxi University,Taiyuan 030006,China
Phase estimation of phase shifts in two arms for an SU(1,1) interferometer with coherent and squeezed vacuum states∗
Qian-Kun Gong(龚乾坤)1,Dong Li(李栋)1,Chun-Hua Yuan(袁春华)1,4,†, Ze-Yu Qu(区泽宇)1,3,and Wei-Ping Zhang(张卫平)2,4
1 Quantum Institute for Light and Atoms,School of Physics and Material Science,East China Normal University,Shanghai 200062,China
2 Department of Physics and Astronomy,Shanghai Jiao Tong University,Shanghai 200240,China
3 Department of Physics,Indiana University–Purdue University Indianapolis,Indianapolis 46202,USA
4 Collaborative Innovation Center of Extreme Optics,Shanxi University,Taiyuan 030006,China
We theoretically study the quantum Fisher information(QFI)of the SU(1,1)interferometer with phase shifts in two arms by coherent⊗squeezed vacuum state input,and give the comparison with the result of phase shift only in one arm. Different from the traditional Mach–Zehnder interferometer,the QFI of single-arm case for an SU(1,1)interferometer can be slightly higher or lower than that of two-arm case,which depends on the intensities of the two arms of the interferometer. For coherent⊗squeezed vacuum state input with a fixed mean photon number,the optimal sensitivity is achieved with a squeezed vacuum input in one mode and the vacuum input in the other.
phase estimation,quantum Fisher information,SU(1,1)interferometer
1.Introduction
Quantum enhanced metrology which has received a lot of attention in recent years is the use of quantum measurement techniques to obtain higher statistical precision than purely classical approaches.[1–16]Mach–Zehnder interferometer(MZI)and its variants were used as a generic model to realize highly precise estimation of phase.In order to achieve the ultimate lower bounds,[17,18]much work has been devoted to finding the methods to improve the sensitivity of phase estimation,such as(i)using the nonclassical input states(quantum resources):squeezed states[3,19,20]and NOON states,[21,22](ii)using the new detection methods:homodyne detection[23,24]and parity detection,[25–28]and(iii)using the nonlinear processes:amplitude amplification[29]and phase magnification.[13]Here we focus on the nonlinear amplitude amplification process to improve the sensitivity.In 1986,Yurke et al.[29]introduced a new type of interferometer where two nonlinear beam splitters(NBSs)take the place of two linear beam splitters(BSs)in the traditional MZI.It is also called the SU(1,1)interferometer because it is described by the SU(1,1)group,as opposed to the traditional SU(2)MZI for BS.The detailed quantum statistics of the two mode SU(1,1)interferometer was studied by Leonhardt.[30]The SU(1,1)phase states were also studied theoretically in quantum measurements for phase-shift estimation.[31,32]Furthermore,the SU(1,1)-type interferometers have been reported by different groups using different systems in theory and experiment,such as allopticalarms,[33–36]allatomic arms,[37–39]atom–light hybrid arms,[40–45]light–circuit quantum electrodynamics system hybrid arms,[46]and all mechanical modes arms.[47]These SU(1,1)-type interferometers provide different methods for basic measurement.
At present,many researchers are focusing on how to measure the phase sensitivities,where several detection schemes have been presented.[23,28,36]In general,it is difficult to optimize all the detection schemes to obtain the optimal estimation protocol.However,the quantum Fisher information (QFI)[4,5]characterizes the maximum amount of information that can be extracted from quantum experiments about an unknown parameter(e.g.,phase shiftφ)using the best(and ideal) measurement device.Therefore,the lower bounds in quantum metrology can be obtained by using the method of the QFI. In recent years,many efforts were made to obtain the QFI of different measurement systems.[48–66]For the SU(1,1)interferometers with phase shift only in one arm,the QFI with coherent states input was studied by Sparaciari et al.,[60,62]and the QFI with coherent⊗squeezed vacuum state input was presented by some of us.[28]Nevertheless in some measurement schemes,phase shifts in two arms are required to measure. For example,the phase sensitivity of phase shifts in two arms for the SU(1,1)interferometer with coherent states input was experimentally studied by Linnemann et al.[37]Jarzyna et al. studied the QFIs of phase shifts in the two-arm case for a MZI, and presented the relationship with the result of phase shift inthe single-arm case.[52]Since phase shift in the single arm is not simply equivalent to the phase shifts in two arms where one phase shift of them is 0,the QFIs of phase shifts in two arms for an SU(1,1)interferometer needed to be researched.In this paper,we study the QFI of SU(1,1)interferometer of phase shifts in two arms with two coherent states input and coherent⊗squeezed vacuum state input,and give the comparison with the result of phase shift only in one arm.These results should be useful for some phase measurement processes.
2.The QFI of phase shifts in two arms for an SU(1,1)interferometer
The QFI ℱ is the intrinsic information in the quantum state and is not related to actual measurement procedure as shown in Fig.1.It establishes the best precision that can be attained with a given quantum probe.[4,5]In this section,we study the QFIs of SU(1,1)interferometer of phase shifts in two arms,and compare them with the results of phase shift only in one arm.
2.1.NBS and phase shifts
In an SU(1,1)interferometer,the NBSs take the place of the BSs in the traditional MZI shown in Fig.1.Firstly,we theoretically describe the NBS briefly,which can be completed by the optical parameter amplifier(OPA)or four-wave mixing (FWM)process.The annihilation operators of the two modes a,b,and the pump field arerespectively.The interaction Hamiltonian for NBS is
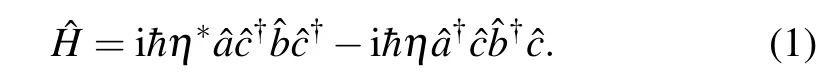
Because the pump field is very strong and the intensity of the pump field is not significantly changed in the mixing process, the initial and final states of the pump field are the same as the coherent state|αpump〉.Under the undepleted pump approximation,the Hamiltonian is written as
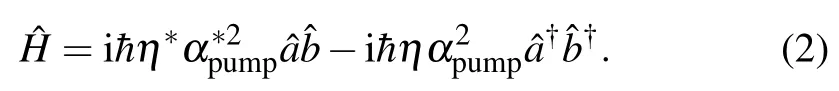
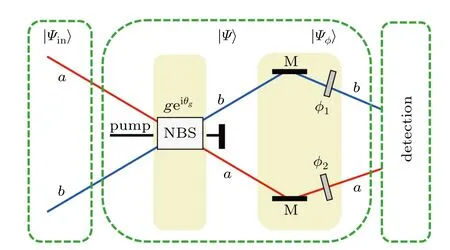
Fig.1.(color online)Schematic diagram of the parameter estimation process based on the SU(1,1)interferometer.g and θg describe the strength and phase in the first NBS process,respectively.a and b denote two light modes in the interferometer.In the Schrödinger picture,the initial state |Ψin〉injecting into a NBS results in the output|Ψ〉,and the state is transformed as|Ψφ〉after phase shifts.NBS:nonlinear beam splitter.φ1,φ2: phase shifts.M:mirrors.
The corresponding time-evolution operator is=is the two-mode squeezing parameter.In the Schrödinger picture,the initial state|Ψin〉injecting into an NBS results in thewhere the transformation of the annihilation operators is
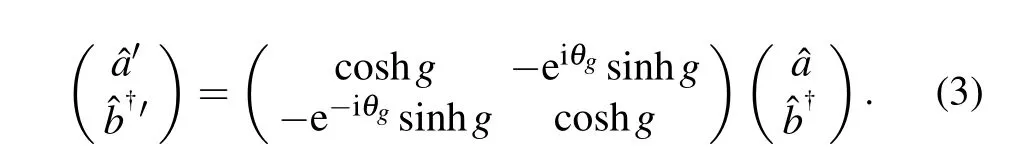
Secondly,we describe the phase shifts process.Different from the BS,the NBS involves three light fields where the pump field is classical and with a classical reference phase. The uncertainty of classical pump fieldis very small and the phase uncertainties are from the modes a and b. After the first NBS,as shown in Fig.1,the two beams sustain phase shifts,i.e.,the mode a and mode b undergo the phase shifts of φ1and φ2,respectively.Then we may write
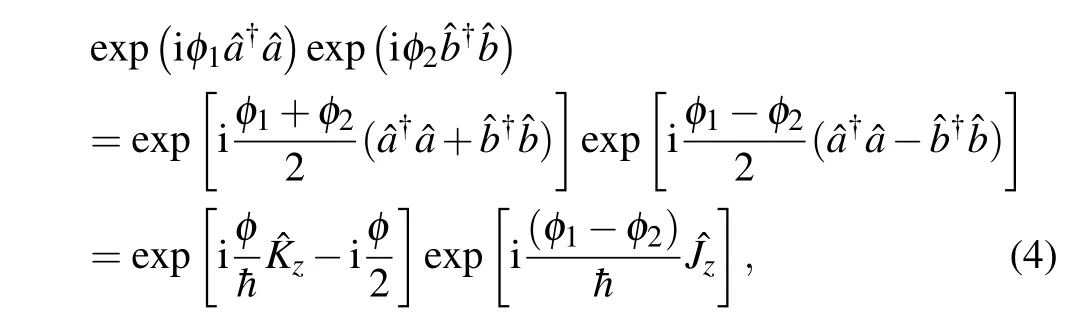
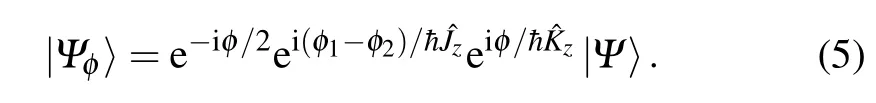
2.2.QFI
The QFI ℱ is defined as[4,5]
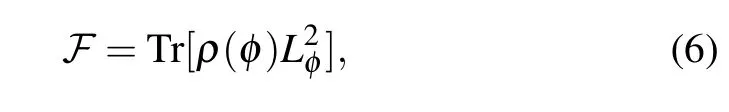
where the Hermitian operator Lφ,called symmetric logarithmic derivative,is defined as the solution of the equation∂φρ(φ)=[ρ(φ)Lφ+Lφρ(φ)]/2.In terms of the complete basis{|k〉}such that ρ(φ)=∑kpk|k〉〈k|with pk≥0 and∑kpk=1,the QFI can be written as[4,5,48–50]

Under the condition of lossless,for a pure state the QFI is reduced to[49,52]

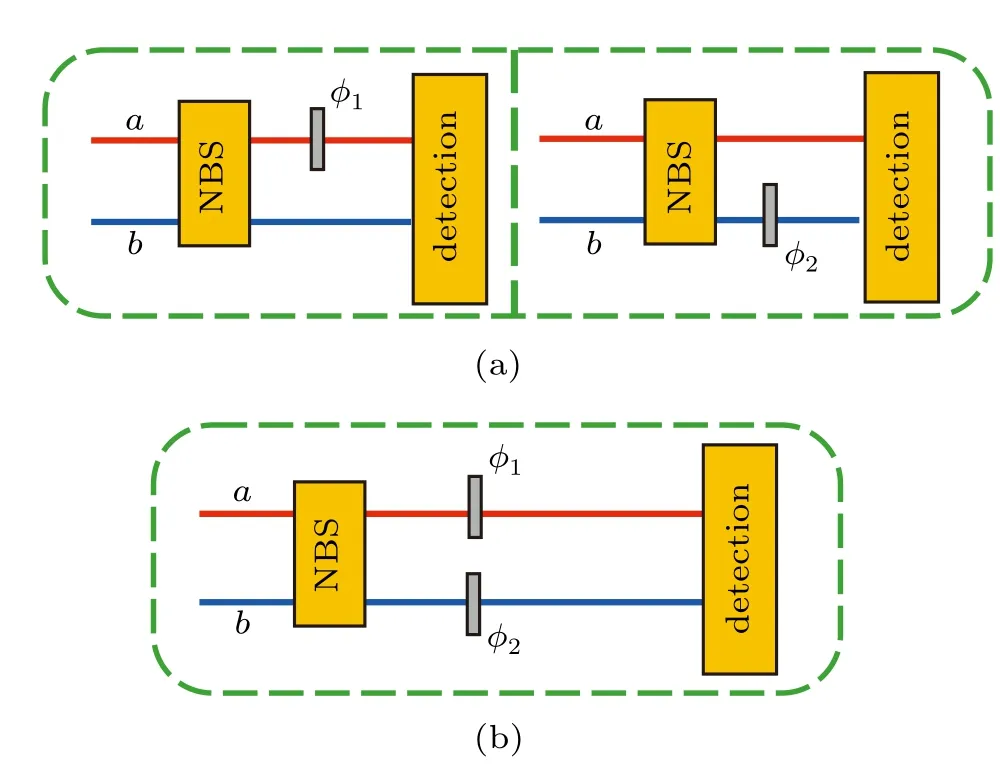
Fig.2.(color online)Different phase delay ways of the interferometer. (a)Phase shift in the single arm is divided into single upper arm and single lower arm due to the fact that the intensities of the two arms are not equal. (b)Phase shifts in the two arms.
Now,we give the QFIs with different input states under the condition of phase shifts in two arms.From Eq.(5),|Ψφ〉is the state vector just before the detection process of the SU(1,1) interferometer andThen from Eq.(8),the QFI can be worked out as

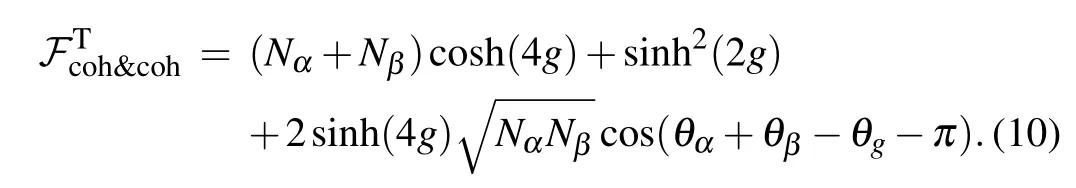
When θα+θβ−θg=π,the maximal QFIis reduced to
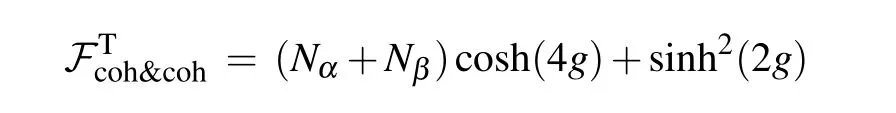
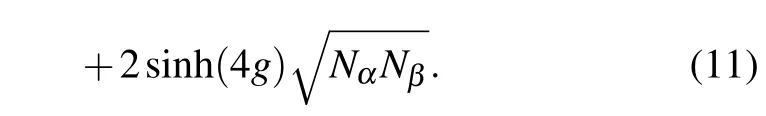
When Nα=Nβ=0(vacuum input)and Nα0,Nβ=0(one coherent state input),from Eq.(11)the corresponding QFIs are given by=sinh2(2g)and=Nαcosh4g+ sinh2(2g),respectively.
Next,we consider a coherent light combined with a squeezed vacuum light as the input|ψin〉=|α〉a⊗|0,ς〉b(α=|α|eiθα,Nα=|α|2,and|0,ς〉b=ˆSb(r)|0〉bis the singlemode squeezed vacuum state in the b-mode wherewith ς=r exp(iθς)the single-mode squeezing parameter),and the QFI can be worked out as
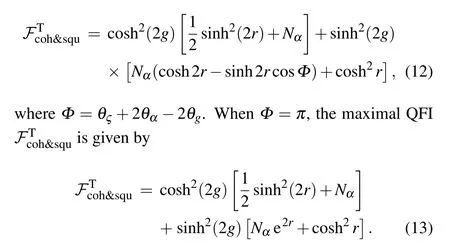
So far,we have given the QFI of SU(1,1)interferometer where the phase shifts in the two arms,and they as well as the QFIs with phase shift in the one arm case are summarized in the Table 1.The QFIs of phase shift in upper arm and in lower arm are also slightly different because the intensities in two arms of the interferometer are unbalanced.The QFI of single-arm case for an SU(1,1)interferometer can be slightly higher or lower than that of double arms case,which depends on the intensities of the two arms of the interferometer.Different from the SU(1,1)interferometer,the QFIs of the phase shifts in single upper arm and in single lower arm are the same due to the intensity balance of the two arms for the MZI.[52]

Table 1.The maximal QFIs of the SU(1,1)interferometer for different phase delay ways with different input states.
3.Quantum Cramér–Rao bound(QCRB)
Whatever the measurement chosen,the QCRB can give the lower bound for the phase measurement[4,5,48–50]
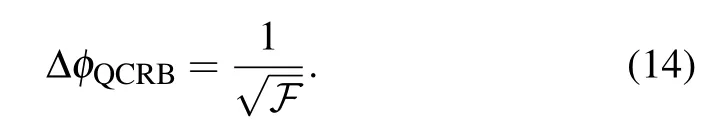
To describe the effect on the QCRB from the unbalanced input state,we introduce a parameter η defined by[24]
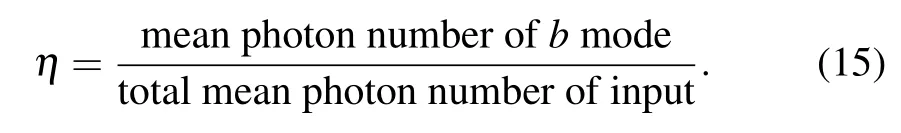
For the two coherent states input,η is equal to Nβ/Nin(Nin= Nα+Nβ),and the optimal phase sensitivities ΔφQCRBas a function of η are shown in Fig.3(a).When η is small, ΔφQCRBfrom the single upper arm case is the best.But when η is large,ΔφQCRBfrom the single lower arm case is the best.ΔφQCRBfrom the two-arm case is always an intermediate value.For a given fixed Ninand the two coherent states input case,the optimal value η is 0.5.Thus for the two coherent states input,the optimal input state isand the corresponding optimal QFI isThe optimal QFIas a function of the total input mean photon number Ninis shown in Fig.4(the blue dotted-dashed line).
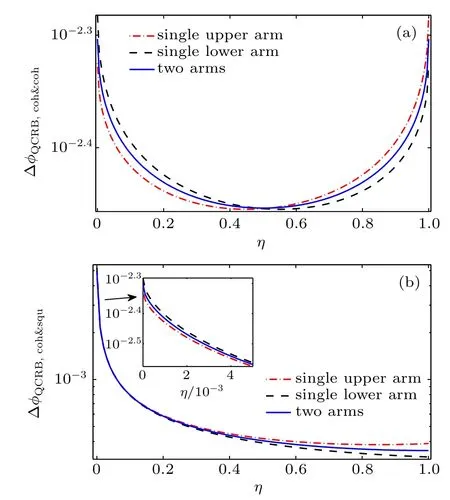
Fig.3.(color online)The QCRB versus the η for(a)two coherent states input and(b)coherent⊗squeezed state input.The inset in panel(b) shows a zoom of the graph for small values of η.Here,N in=200 and g=1.5.
For coherent⊗squeezed vacuum state input,η is equal to sinh2r/Nin(Nin=Nα+sinh2r),where the parameter η can be used to label the squeezing fraction of the mean photon number.When η=0 or η=1,the input state is only a coherent state|α〉aor only a squeezed vacuum state|0,ζ〉b.When 0<η<1,the input state is a coherent⊗squeezed vacuum state. For coherent⊗squeezed vacuum state input case,only the squeezed vacuum light as input and without the coherent state, the phase sensitivity is the highest shown in Fig.3(b).The optimal input state is|0〉⊗|0,ζ〉,and the corresponding optimal QFI is=(1+Nin)[2Nincosh2(2g)+sinh2(2g)], which is different from the commonly used optimal input state within MZI.[55,67,68]The reason is the number fluctuations and Pasquale et al.[69]have given the same result for generic two-mode interferometric setup recently.The optimal QFIas a function of Ninis shown in Fig.4(the red dashed line).For a fixed mean photon number(with number fluctuations),Hofmann suggested the form of Heisenberg limit is,which indicates averaging over the squared photon numbers.[70]In our proposalis defined asIn Fig.4,the black solid line is the Hofman limit for coherent⊗squeezed vacuum state input under the optimal condition.
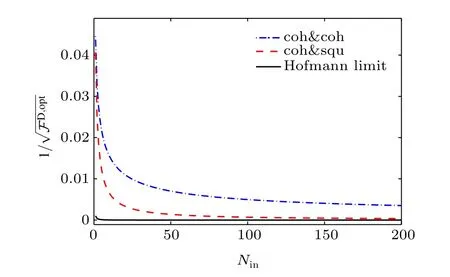
Fig.4.(color online)The optimal QFIs versus the total input mean photon number N in.The dotted-dashed line and the dashed line are the two coherent states input and coherent⊗squeezed state input,respectively.The solid line is the Hofmann limit with coherent⊗squeezed state input g=1.5.
For the lossy interferometers,the pure states evolve into the mixed states and the QFI will be reduced.However,the QFI of pure state puts an upper bound on that of mixed state. Here,we focus on the maximal QFI of the SU(1,1)interferometer,and then we ignore the losses in the interferometer.
4.Conclusion
The analytical expressions of QFI for an SU(1,1)interferometer with two coherent states and coherent⊗squeezed vacuum state inputs have been derived.For single-arm case, the QCRBs of phase shift in upper arm and in lower arm are slightly different because the intensities in two interferometric arms are asymmetric.The phase sensitivities of phase shifts between the single-arm case and two-arm case are also compared.The QCRB of single-arm case can be slightly higher or lower than that of two-arm case,which depends on the intensities of the two arms of the interferometer.For coherent state⊗squeezed vacuum state input with a definite input number of photons,the optimal condition to obtain the highest phase sensitivity is a squeezed vacuum in one mode and the vacuum state in the other mode.
[1]Helstrom C W 1976 Quantum Detection and Estimation Theory(New York:Academic)
[2]Holevo A S 1982 Probabilistic and Statistical Aspect of Quantum Theory(Amsterdam:North-Holland)
[3]Caves C M 1981 Phys.Rev.D 23 1693
[4]Braunstein S L and Caves C M 1994 Phys.Rev.Lett.72 3439
[5]Braunstein S L,Caves C M and Milburn G J 1996 Ann.Phys.247 135
[6]Lee H,Kok P and Dowling J P 2002 J.Mod.Optic.49 2325
[7]Giovannetti V,Lloyd S and Maccone L 2006 Phys.Rev.Lett.96 010401
[8]Zwierz M,Pérez-Delgado C A and Kok P 2010 Phys.Rev.Lett.105 180402
[9]Giovannetti V,Lloyd S and Maccone L 2004 Science 306 1330
[10]Giovannetti V,Lloyd S and Maccone L 2011 Nat.Photonics 5 222
[11]Ou Z Y 2012 Phys.Rev.A 85 023815
[12]Abbott B P,et al.2016 Phys.Rev.Lett.116 061102
[13]Hosten O,Krishnakumar R,Engelsen N J and Kasevich M A 2016 Science 352 1552
[14]Xiang G Y and Guo G C 2013 Chin.Phys.B 22 110601
[15]Zhang L J and Xiao M 2013 Chin.Phys.B 22 110310
[16]Wei C P,Hu XY,Yu YF and Zhang Z M 2016 Chin.Phys.B 25 040601
[17]Zwierz M,Pérez-Delgado CAand Kok P 2012 Phys.Rev.A 85 042112
[18]Pezzè L,Hyllus P and Smerzi A 2015 Phys.Rev.A 91 032103
[19]Xiao M,Wu L A and Kimble H J 1987 Phys.Rev.Lett.59 278
[20]Grangier P,Slusher R E,Yurke B and LaPorta A 1987 Phys.Rev.Lett. 59 2153
[21]Dowling J P 2008 Contemp.Phys.49 125
[22]Boto A N,Kok P,Abrams D S,Braunstein S L,Williams C P and Dowling J P 2000 Phys.Rev.Lett.85 2733
[23]Li D,Yuan C H,Ou Z Y and Zhang W 2014 New J.Phys.16 073020
[24]Hu X Y,Wei C P,Yu Y F and Zhang Z M 2016 Front.Phys.11 114203
[25]Anisimov P M,Raterman G M,Chiruvelli A,Plick W N,Huver S D, Lee H and Dowling J P 2010 Phys.Rev.Lett.104 103602
[26]Gerry C C and Mimih J 2010 Contemp.Phys.51 497
[27]Chiruvelli A and Lee H 2011 J.Mod.Optic.58 945
[28]Li D,Gard B T,Gao Y,Yuan C H,Zhang W,Lee H and Dowling J P 2016 Phys.Rev.A 94 063840
[29]Yurke B,McCall S L and Klauder J R 1986 Phys.Rev.A 33 4033
[30]Leonhardt U 1994 Phys.Rev.A 49 1231
[31]Vourdas A 1990 Phys.Rev.A 41 1653
[32]Sanders B C,Milburn G J and Zhang Z 1997 J.Mod.Optic.44 1309
[33]Hudelist F,Kong J,Liu C,Jing J,Ou Z Y and Zhang W 2014 Nat. Commun.5 3049
[34]Anderson B E,Gupta P,Schmittberger B L,Horrom T,Hermann-Avigliano C,Jones K M and Lett P D 2016 arXiv:1610.06891v1 [quant-ph]
[35]Plick W N,Dowling J P and Agarwal G S 2010 New J.Phys.12 083014
[36]Marino A M,Corzo Trejo N V and Lett P D 2012 Phys.Rev.A 86 023844
[37]Linnemann D,Strobel H,Muessel W,Schulz J,Lewis-Swan R J, Kheruntsyan K V and Oberthaler M K 2016 Phys.Rev.Lett.117 013001
[38]Gabbrielli M,Pezzè L and Smerzi A 2015 Phys.Rev.Lett.115 163002
[39]Gross C,Zibold T,Nicklas E,Estève J and Oberthaler M K 2010 Nature 464 1165
[40]Chen B,Qiu C,Chen S,Guo J,Chen L Q,Ou Z Y and Zhang W 2015 Phys.Rev.Lett.115 043602
[41]Chen Z D,Yuan C H,Ma H M,Li D,Chen L Q,Ou Z Y and Zhang W 2016 Opt.Express 24 17766
[42]Jacobson J,Björk G and Yamamoto Y 1995 Appl.Phys.B 60 187
[43]Haine S A 2014 Phys.Rev.Lett.112 120405
[44]Szigeti S S,Tonekaboni B,Lau W Y S,Hood S N and Haine S A 2014 Phys.Rev.A 90 063630
[45]Haine S A and Lau W Y S 2016 Phys.Rev.A 93 023607
[46]Barzanjeh S,DiVincenzo D P and Terhal B M 2014 Phys.Rev.B 90 134515
[47]Cheung H F H,Patil Y S,Chang L,Chakram S and Vengalattore M 2016 arXiv:1601.02324v1[quant-ph]
[48]Toth G and Apellaniz I 2014 J.Phys.A 47 424006
[49]Pezzè L and Smerzi A 2014 in Proceedings of the International School of Physics“Enrico Fermi”,Course CLXXXVIII“Atom Interferometry”edited by Tino G and Kasevich M(Societ`a Italiana di Fisica and IOS:Bologna),p.691
[50]Demkowicz-Dobrzanski R,Jarzyna M and Kolodynski J 2015 Prog. Optics 60 345
[51]Wang X B,Hiroshima T,Tomita A and Hayashi M 2007 Phys.Rep. 448 1
[52]Jarzyna M and Demkowicz-Dorbrzanski R 2012 Phys.Rev.A 85 011801(R)
[53]Monras A 2013 arXiv:1303.3682v1[quant-ph]
[54]Pinel O,Jian P,Treps N,Fabre C and Braun D 2013 Phys.Rev.A 88 040102(R)
[55]Liu J,Jing X and Wang X 2013 Phys.Rev.A 88 042316
[56]Gao Y and Lee H 2014 Eur.Phys.J.D 68 347
[57]Jiang Z 2014 Phys.Rev.A 89 032128
[58]Li Y L,Xiao X and Yao Y 2015 Phys.Rev.A 91 052105
[59]Safranek D,Lee A R and Fuentes I 2015 New J.Phys.17 073016
[60]Sparaciari C,Olivares S and Paris M G A 2015 J.Opt.Soc.Am.B 32 1354
[61]Ren Y K,Tang L M and Zeng H S 2016 Quantum Inf.Process.15 5011
[62]Sparaciari C,Olivares S and Paris M G A 2016 Phys.Rev.A 93 023810
[63]Strobel H,Muessel W,Linnemann D,Zibold T,Hume D B,Pezze L, Smerzi A and Oberthaler M K 2014 Science 345 424
[64]Lu X M,Yu S and Oh C H 2015 Nat.Commun.6 7282
[65]Hauke P,Heyl M,Tagliacozzo L and Zoller P 2016 Nat.Phys.12 778
[66]Liu P,Wang P,Yang W,Jin G R and Sun C P 2017 Phys.Rev.A 95 023824
[67]Pezzè L and Smerzi A 2008 Phys.Rev.Lett.100 073601
[68]Lang M D and Caves C M 2013 Phys.Rev.Lett.111 173601
[69]Pasquale A D,Facchi P,Florio G,Giovannetti V,Matsuoka K and Yuasa K 2015 Phys.Rev.A 92 042115
[70]Hofmann H F 2015 Phys.Rev.A 79 033822
10 March 2017;revised manuscript
9 May 2017;published online 31 July 2017)
10.1088/1674-1056/26/9/094205
∗Project supported by the National Natural Science Foundation of China(Grant Nos.11474095,11654005,and 11234003)and the National Key Research and Development Program of China(Grant No.2016YFA0302000).
†Corresponding author.E-mail:chyuan@phy.ecnu.edu.cn
©2017 Chinese Physical Society and IOP Publishing Ltd http://iopscience.iop.org/cpb http://cpb.iphy.ac.cn
杂志排行
Chinese Physics B的其它文章
- Improved control for distributed parameter systems with time-dependent spatial domains utilizing mobile sensor actuator networks∗
- Geometry and thermodynamics of smeared Reissner–Nordström black holes in d-dimensional AdS spacetime
- Stochastic responses of tumor immune system with periodic treatment∗
- Invariants-based shortcuts for fast generating Greenberger-Horne-Zeilinger state among three superconducting qubits∗
- Cancelable remote quantum fingerprint templates protection scheme∗
- A high-fidelity memory scheme for quantum data buses∗
