井眼轨迹预测及井眼轨迹三维可视化系统开发

马玉凤， 袁野

(东北石油大学 1. 计算机与信息技术学院学院; 2. 计算机与信息技术学院学院, 大庆 163318)

井眼轨迹预测及井眼轨迹三维可视化系统开发

马玉凤1， 袁野2

(东北石油大学 1. 计算机与信息技术学院学院; 2. 计算机与信息技术学院学院, 大庆 163318)

对钻井施工过程中的问题进行了调查，并对钻井井底盲区测量问题及对现行的井眼轨迹三维可视化系统进行了研究。对井眼轨迹测点方位计算问题，选取了符合我国国情的石油钻井圆柱螺线法，提出了方便利用计算机计算的算法并对其进行了简化。研究了基于支持向量机进行井眼轨迹预测的方法，并建立井眼轨迹预测的支持向量机模型；对井眼轨迹相关数据进行预测，并利用预测的数据进行各测点的测斜计算，构建井眼轨迹预测点，方便对其进行三维可视化；对基于切片法的井眼轨迹桶状建模进行了研究，并构建各点井筒切片，依次连接各切片。利用OpenGL实现了通过井眼估计预测数据进行井眼轨迹的三维可视化可视化软件开发，为钻井生产的成功施工提供帮助和指导。

三维可视化； 井眼轨迹预测； OpenGL； 支持向量机； 切片

0 引言

随着石油钻井工程技术的进步和发展，导向井与水平井的日益增多，井眼轨迹预测一直是钻井工程研究的热点。特别是在钻井施工过程中，需要随时定性、定量地通过随钻测量(MWD)传感器对井眼轨迹数据进行反馈，但是由于传感器距离钻头一般有8-20米的测量盲区距离，因此常规的井眼轨迹三维可视化方式并不能反应出钻头的实际位置与盲区井眼状况，这给实际生产中精确井眼轨迹控制带来了困难。目前国内外常用的井眼轨迹三维可视化系统一般忽略了井眼轨迹预测的方法的优化，现行的预测方法一种是基于底部钻具组合(BHA)受力的分析方法，这种方法计算过程复杂，并且需要特定的场合才有使用条件[1-5]。另一种仅仅是通过基于井眼轨迹预测的几何方法的数据分析[6,7]，这种单一的数据分析不能很好的反应井底状态，再次这种方法虽然简单但是预测结果存在较大误差。为此，在分析现场生产的几个主要影响因素的基础上，选择利用基于支持向量机的井眼轨迹预测方法分析井眼盲区。

1 井眼轨迹的计算

在钻井生产中，测得的数据被称为测斜数据，井眼轨迹计算的本质就是通过对现场采集的井眼轨迹的三大主要测斜数据——井深、井斜、方位角——进行测斜计算[8]。而测斜计算又是水平井井眼方位的根本，一般认为钻井生产中的井下钻井轨道是一条平滑连续的空间曲线。但是，经过MWD传感器测得的数据只是相对离散的各个测点的基本参数，无法知道连续的两测点之间井眼轨道的实际形态，因此测斜计算方法都是在特定的假设基础上建立的。所以在这里选用经由圆柱螺线法推导而来的校正平均角法来进行测斜计算[9-10]，这是由于我国的钻井方式多为旋转转盘式钻进方式，在这种钻进方式中井下管柱的轨道形态近似的看作是沿着圆柱壁行进的圆柱螺线，如图1所示。

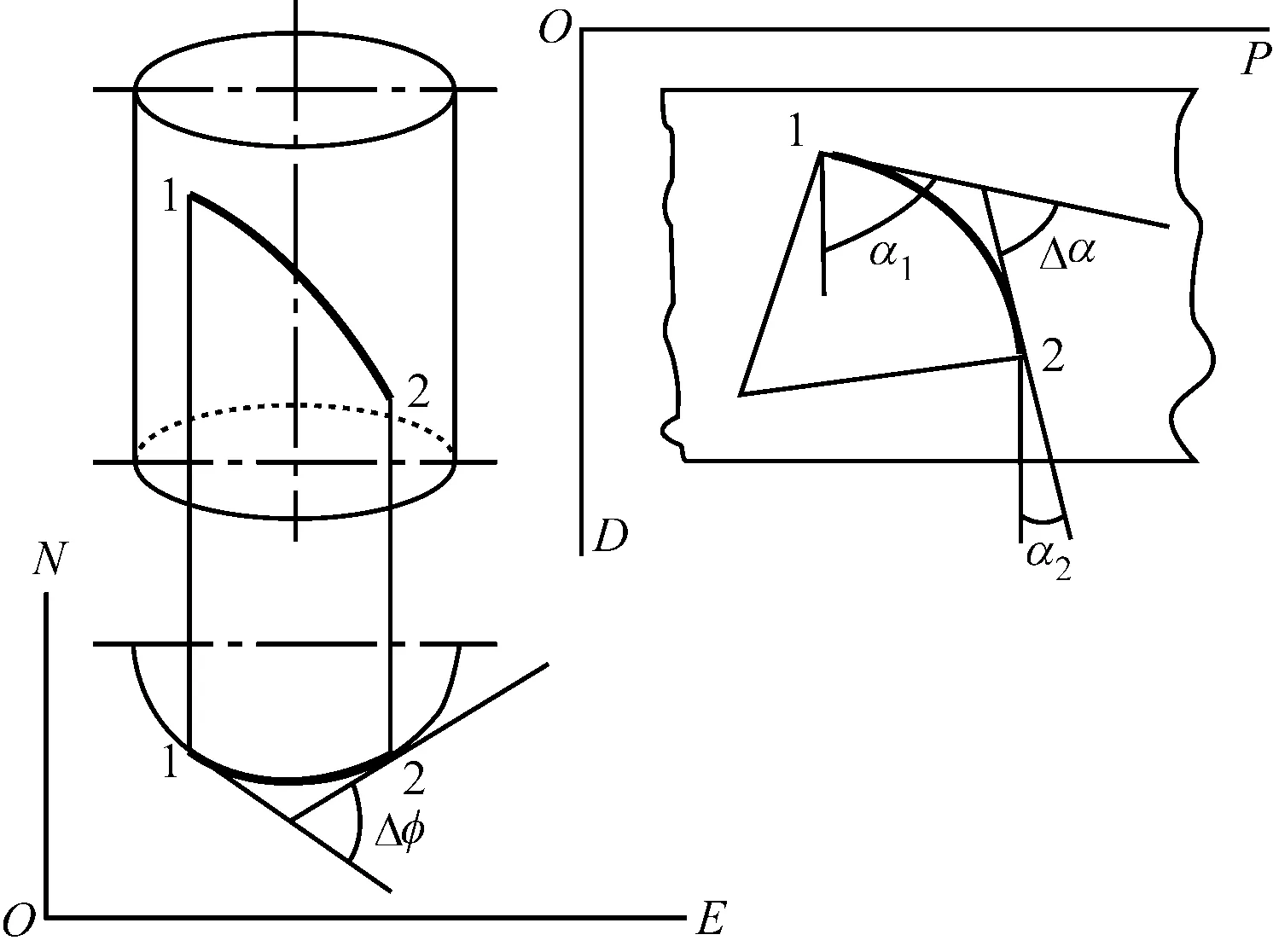
图1 圆柱螺线法的示意图

圆柱螺线法假设两测点间的测段为一条等变螺旋角的圆柱螺线，螺线在两段点处与上、下两测点的井眼方向线相切。其在水平投影图上是圆弧；在垂直剖面图上也是圆弧，如式(1)。

(1)

但是实际计算中Δα和Δφ这两个增量中任一个或同时为零时，都需要另选公式计算。所以在这里通过三角变换等方法对圆柱螺线法进行简化，可以得到校正平均角法，如式(2)

(2)

再通过上述公式所求的增量数据，就可以得没个测点的坐标，计算公式(3)。

(3)

在上述公式中：ΔE为东西位移增量；ΔN为南北位移增量；Δ为垂深增量；ΔS为水平投影长度增量；ΔL为井深侧段长度；α1、α2、Δα分别表示上下两测点处的井斜角和井斜角变化量；φ1、φ2、Δφ分别表示上下两测点处的方位角和方位角变化量.

2 基于支持向量机的井眼轨迹预测

用于非线性回归估计的支持向量机的基本思想是通过用内积函数定义的非线性变换将输入空间变换到一个高维空间，然后在这个高维空间中寻找输入变量和输出变量之间的某种线性关系[11，12]。

支持向量机算法是一个凸二次优化问题，保证找到的解是全局最优解并能较好地解决小样本、非线性、高维数等实际问题，特别是其小样本学习能力要远远优于传统的神经网络算法[13]。

类似于神经网络方法，用支持向量机进行参数的回归估计和在线预测，首先要选择训练样本。因此，在构造支持向量机的过程中，可通过选取BHA结构、钻进方式及已钻井眼轨迹等参数作为SVM学习和预测时的输入特征向量。经反复试验分析，选取如下5个参数作为特征输入向量:① 当前测点的井斜角x1；② 当前测点的钻进方式x2；③ 上一测点的钻进方式x3；④ 当前测点与上一测点间井段的井眼曲率x4；⑤ 上一测点与上上一测点间井段的井眼曲率x5。其中，x2和x3两个输入量反映了BHA结构及钻进方式的影响，x4和x5两个输入量反映了已钻井眼轨迹的影响，而x1输入量选用当前测点井斜角的目的是因为当前测点离钻头最近，同时也为了避免由于样本十分近似或完全一样而使学习过程出现不收敛的现象。此外，将钻头处的定曲率几何预测值与真实值的差值作为目标输出y，若记式(4)。

(4)

这样，由设一个集为{(Xi,Yi)}，i=1,2,…,1)},Xi∈RN为输入，Yi∈R为输出，l为样本数。

在此基础上假设所有样本数据都可以无误差的在精度ε通过非线性函数拟合，即得式(5)

(5)

用于拟合的非线性函数的形式如式(6)。

(6)

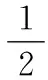
(7)

最终变为下面的优化问题如式(8)。

(8)

式中，C为惩罚系数，C越大表示对超出误差ε的数据点惩罚越大，C>0。

显然，这就是一个二次规划的非线性约束问题，这里可以采用拉格朗日乘子法，并引入核函数K(Xi,Yi)=[φ(Xi),φ(Yi)]，最终可以得到标准的二次规划问题形式，如式(9)。

(9)

其中

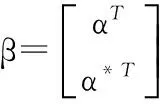
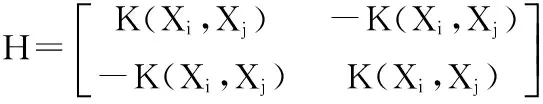
D=[ε-Y1,ε-Y2,…,ε-Y1,ε+Y1,ε+Y2,…,ε+Y2]T.

其中b可由标准支持向量求得，而核函数选择高斯核函数(RBF)[12]。

这样通过选取几口井有代表性的井，通过用这些井的井眼轨迹参数为样本，其中方差为106.2；惩罚系数C取90000；误差为0.05。以此对支持向量机进行训练后，既可用于其他井的井眼轨迹预测。SVM法与定曲率法井眼轨迹预测对比图，如图2所示。

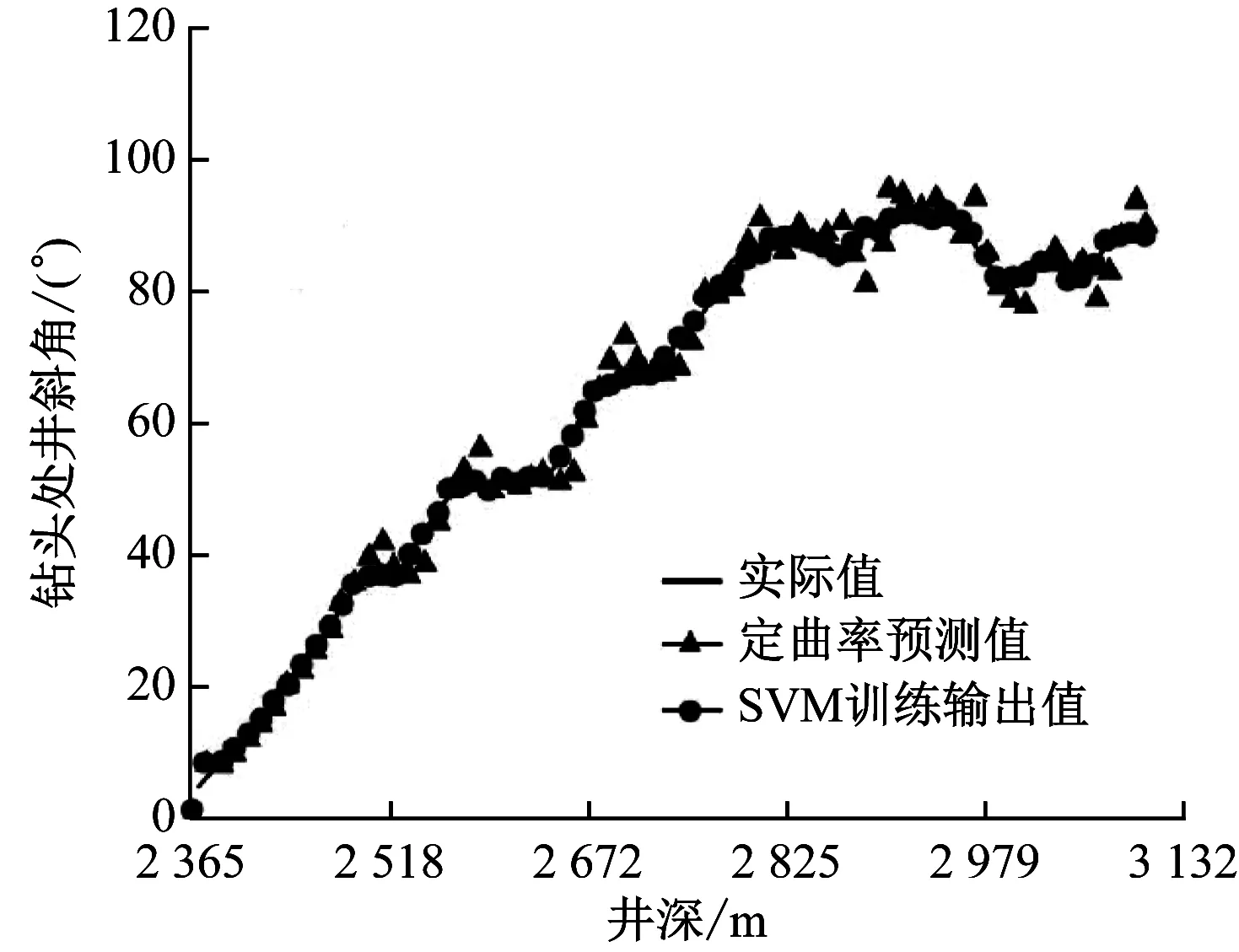
图2 SVM法与定曲率法井眼轨迹预测对比图

可以看到基于SVM的井眼轨迹盲区预测方法简单有效且预测精度远远高于传统的定曲率法。

3 三维井眼轨迹的绘制

由于在在水平井钻井实钻生产过程中受到各种地层应力的作用，钻头会发生不同程度的偏移，所以水平井的井眼轨迹不能简单的看做是由圆柱体构成。在将井眼轨迹筒状化时，若按圆柱体在测点间首尾连接在连接部位就会出现缝隙，这就需要对缝隙进行进一步处理，这样会极大的增加对缝隙处数据处理的计算量，造成系统的交互操作也不灵活。所以这里利用切片法[14]对井眼轨迹进行桶状绘制。

3.1 切片上全局坐标的计算

设全局坐标原点切片是以井筒半径R为半径、以全局坐标原点O为圆心的圆(设为圆O)，然后沿逆时针方向、以全

局坐标x轴为起点，将这个圆等分为n份，并得到圆O上对应的等分点Q0，则Q0的全局坐标与局部坐标Q′(x′,y′,z′)相等。然后再根据Q0点坐标计算目标切片等分点Q的全局坐标。在计算目标切片的全局坐标时首先将圆O沿全局坐标轴平移，使圆心O和目标切片圆心P点重合。再分别顺时针绕全局坐标x和z轴将圆O旋转一定角度(设为α、β)，Q0与目标等分点Q点重合。由三维平移和旋转变换公式得Q点全局坐标,为式(11)。

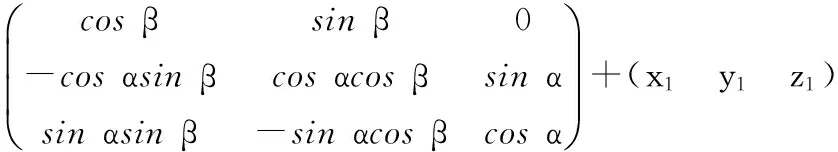
(11)

其中(x1y1z1)为Q点的全局坐标。

3.2 构建切片间的侧面

首先假设初始点P的坐标为00(记为P00点)，然后依次可以得到该切片上的n个等分点P00,P01,P02,…,P0n，再加入下一个切片的初始等分点P10后，其与P00、P01这时构成了第一个三角形；在加入P11，其与P10、P01这时构成了新的三角形。所以每加入一个点就与上一个三角形上的相邻的两个点构成一个新的三角形，这样相邻切片的侧面就有这些三角形构成了。然后利用OpenGL中的相关技术对三角形进行处理，就可以形成逼真的桶装三维井眼轨迹，如图3所示。

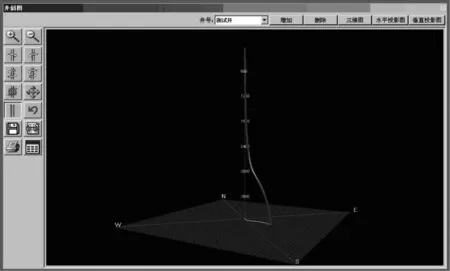
图3 桶装三维井眼轨迹

4 总结

本文利用基于支持向量机的井眼轨迹预测方法，总体上优于传统的几何预测法，能够很好的反应井底盲区的情况，有利于现场工作人员对井眼轨迹井眼轨迹进行控制，减少事故发生、改善钻井质量、降低生产能耗，从而提高生产效率。

[1] 张建群,阎铁.钻头与地层相互作用分析及井眼轨迹预测[J].石油学报,1991,12(4):102-109.

[2] 高德利.井眼轨迹控制问题的力学分析方法[J].石油学报,1996,17(1):115-121.

[3] HO H S. Prediction of drilling trajectory in directional wells via a new rock-bit interaction model[R].SPE16685,1987.

[4] Larspm P A. Three-dimensional, quasi-static,drill ahead BHA model for wellbore trajectory prediction and controls [R].SPE 23530,1991.

[5] Dahi T, Schmalhortst B.A new bottom hole assembly analysis program for the prediction of the bore hole path based on a sophisticated static algorithm[R].SPE21948,1991.

[6] 刘修善,石在虹,周大千.训一算井眼轨道的曲线结构法[J].石油学报，1994, 15(3): 126-133.

[7] 刘修善,艾池,王新清.井眼轨迹插值法[J].石油钻采工艺,1997,19(2):11-15.

[8] 刘巨保,岳欠杯.石油钻采管柱力学[M].北京：石油工业出版社,2011:1-17.

[9] Boyun Guo,Robert L.Lee,Stefan Miska.Constant-Curvature Equations Improve Design of 3D Well Trajectory[J].Oil & Gas Journal,1993.

[10] 韩志勇.定向钻井设计与计算[M].北京:北京石油大学出版社,2007:53-71.

[11] VAPNIK V N.统计学习理论的本质[M].张学工,译.北京:清华大学出版社,2000.85-124.

[12] VAPNIK V N.The nature of statistical learning theory [M].New York:Springer-Verlag,1999. 225-259.

[13] 史清江,王延江.用于非线性回归估计的支持向量机[A].贾磊.中国自动化学会第19届青年学术会议论文集[C].济南:山东大学出版社,2004:279 -284.

[14] 韩西安,杨海涛,邱铭铭,赵东杰.基于切片图像的血管三维重建方法[J].装备指挥技术学院学报,2002,13(3):85-90.

Development of Wellbore Trajectory Prediction and 3D Visualization System of Borehole Trajectory

Ma Yufeng1， Yuan Ye2

(1. School of Computer and Information Technology; 2. School of Computer and Information Technology; Northeast Petroleum University， Daqing 163318， China)

The problems in the construction process of drilling and drilling bottom blind measurement were studied. The current trajectory of 3D visualization system was designed. The trajectory measuring point range was analyzed. The cylinder helix method which is drilling in Chinese oil situation, was simplified for computer calculation. A wellbore trajectory prediction algorithm based on support vector machine was studied, and its model was established by using support vector machine. The prediction data of well trajectory, and the prediction data of each measuring point were calculated and well trajectory the prediction points were constructed for the convenience of 3D visualization of the barrel. The trajectory modeling based on slicing method was studied, as well as construction of shaft section. The OpenGL was used to realize the visualization of the borehole trajectory by the prediction data of the borehole, which can help and guide the successful construction of the drilling production.

3D visualization; Well trajectory prediction; OpenGL; Support vector machine； Slices

马玉凤(1990-)，女，硕士，研究方向：数字多媒体技术。 袁 野(1987-)，男，硕士，研究方向：仿真与可视化建模。

1007-757X(2017)08-0065-03

TP311

A

2017.03.08)