混凝土面板堆石坝应力变形有限元分析

韩 雪

(通河县水务技术服务中心，黑龙江 通河 150900)

混凝土面板堆石坝应力变形有限元分析

韩 雪

(通河县水务技术服务中心，黑龙江 通河 150900)

近年来，随着新理论和新方法的成功应用，坝工设计水准和现代化施工水平不断进步，混凝土面板堆石坝已成为应用最广泛的当前主流坝型之一。面板堆石坝中新技术的应用不仅简化了施工工序，同时保证了大坝的安全防汛度汛。文章结合工程实例，运用三维有限元计算软件计算了坝体及面板在施工期和蓄水期的应力变形分布规律，分析总结出面板坝在设计施工和运行管理时的特点，得出的结论对实际工程的设计施工带来一定的参考意义。

混凝土；面板堆石坝；应力变形；有限元；分析

0 前 言

混凝土面板堆石坝主要是上下游的堆石体支撑坝体结构，主要防渗结构为上游表面的混凝土面板，这种坝型应用较为普遍。特点是安全性高、施工方便、机械化施工，节省工期和工程造价，正是基于这些特点，目前被国内外在建众多大坝采用，成为首选坝型。

混凝土面板堆石坝从自身材料性质上来说具有以下特点[1]：堆石体层层碾压、大坝分区材料分别填筑、上游迎水面混凝土面板及、趾板以及多层止水。混凝土面板堆石坝本身兼具土石坝的特点，一定程度上克服了二者的局限性；堆石料可以就近取材，节省费用；施工速度快，大仓面薄层振动碾压施工；迎水面采用混凝土面板防渗，防渗效果突出；机械化施工程度高，工期得到保证；施工工艺较为简单适用，因为堆石坝自身过水的特点，直接影响工程导流和防汛度汛；施工过程受外界影响小比如高温、降雨等环境因素，工程进度加快；堆石料可就近采用开挖料。故混凝土面板堆石坝极具安全性和经济适应性。

1 有限元分析计算原理

1.1 材料非线性计算原理

堆石坝材料属于粗粒土，应力变形包括含材料非线性和几何非线性，一般情况下只认为存在材料非线性，单元的几何关系式表达如下：

{ε}=[B]{δ}e

(1)

(2)

式中：{F}e为单元节点力列向量；{δ}e为位移列向量。

材料非线形问题的应力与应变的关系表达为：

f({σ}，{ε})=0

(3)

这种非线形关系的[D]随应力发生变化，故劲度矩阵[K]随之变化，关系式表达为：

[K({δ})]{δ}=[R]

(4)

1.2 邓肯-张E-B模型

E-B模型[2]是在土料三轴试验基础上，将土体的偏应力与轴向应变的曲线变化近似认为其是双曲线。

1)切线弹性模量：

Et=K(1-RfS)2Pa(σ3/Pa)n

(5)

采用卸荷变形模量：

Eur=KurPa(σ3/Pa)d

(6)

2) 切线体积模量：

Bt=KbPa(σ3/Pa)m

(7)

工程实际上限制Bt取值在Et/3至17Et之间。

3) 模型参数

模型各参数需由三轴试验来确定。坝体一般分为主、次堆石区、垫层料区和过渡区等，各分区材料的参数值均不相同。

4)用E-B模型时的弹性矩阵：

B=E/3(1-2μ)

(8)

1.3 中点增量法

在工程实际运用中极为广泛，推导过程较为简单，在非线性有限元的分析方法被广泛应用。它对施工过程荷载加载部分进行模拟，分别求得施工过程的各阶段的材料的应力变形情况。其计算步骤如下[3]：

1)定义初始状态点Mi-1。可通过应力{σ}i-1计算求得材料的弹性常数Ei-1，vi-1然后形成劲度矩阵[K]i-1。

2)施加荷载：在结构上施加一半荷载{△R}i/2，解得位移增量。

(9)

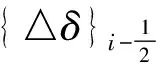
4)利用{R}i-1在结构上施加全荷载{△R}i，解得位移增量

(10)

求解出应力增量{△σ}i、应变增量{△ε}i，并对求出的应力和应变分量进行累加重复1-4的步骤，最终求解处施加各级荷载下对应增量的应力应变。

2 工程实例

某水利枢纽工程主要效益为供水灌溉，兼具发电防洪功能，控制流域面积308.6km2，水库正常蓄水位649.3m，总库容0.96亿m3。电站总装机40MW。工程主要建筑物为混凝土面板堆石坝、溢洪道、引水发电隧洞、电站组成[4]。

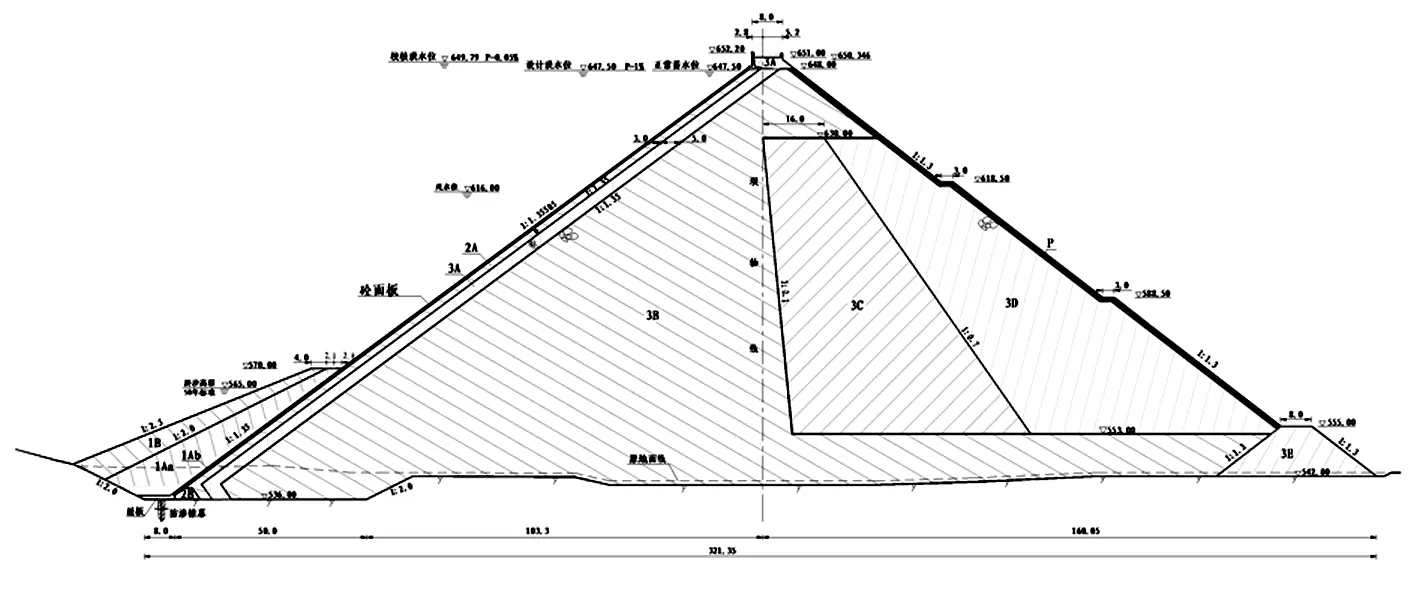
图1 混凝土面板堆石坝标准剖面图

2.1 计算模型

“啊，再有机会？这是诀别之语啊！琼儿要告诉羽弟：琼儿要与他生死与共。”最后一句是萧琼喊出来的。她含泪冲出了书屋。“琼儿不可以！”萧夫人追出书屋，可萧琼不顾母亲阻拦去马厩牵马也不备鞍就驭马冲出了萧家大院。

计算模型采用六面体八节点等参单元进行网格剖分，该模型单元类型根据坝体分区结构分为5种，共划分单元16268个，节点45172个。

2.2 计算参数

据工程设计方的材料试验检测报告，堆石体各分区材料的特性参数见表1。

表1 堆石体材料参数表

2.3 计算结果

2.3.1 坝体

竣工期最大横剖面的计算结果分别见图2-5，位移单位，m，应力单位，Pa。

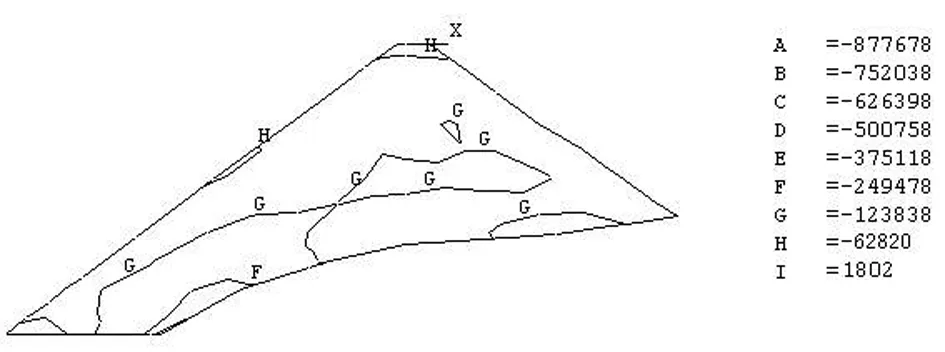
图2 坝体最大横剖面断面小主应力

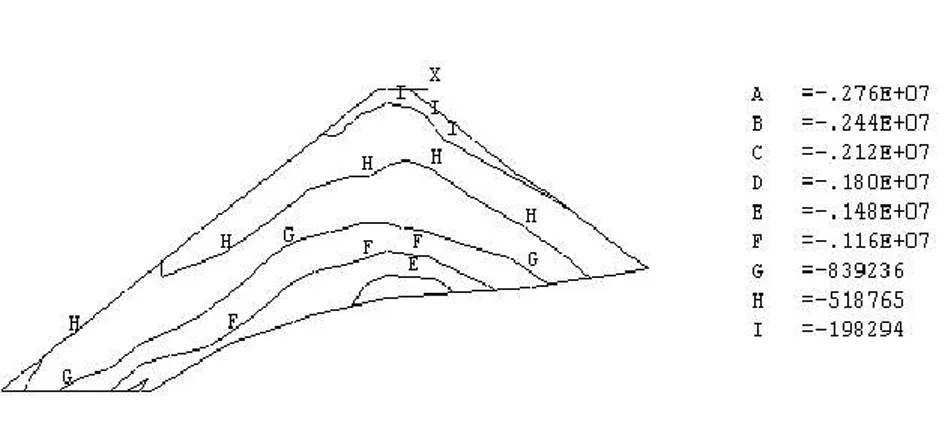
图3 坝体最大横剖面断面大主应力

图4 坝体最大横剖面断面水平位移

图5 坝体最大横剖面断面竖直位移

竣工期坝体最大沉降量从平面图上看基本位于河槽最深处，最大值为40.82cm,大约在坝体1/2位置处，；最大水平位移在上游大约2/3大坝位置处，最大值为5.15cm,，下游最大位移8.22cm,和上游最大位移位置相似，发生于左岸岸坡处；最大、小主应力均产生在坝体底部，最值为2.78MPa和0.85MPa。

2.3.2 面板

图6 面板顺坡向应力

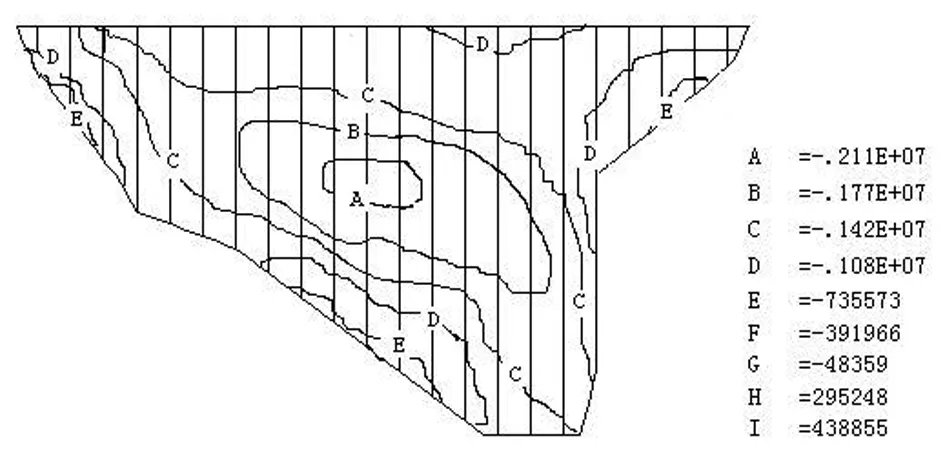
图7 面板轴向应力

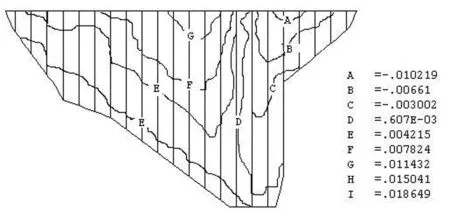
图8 面板顺坡向变形

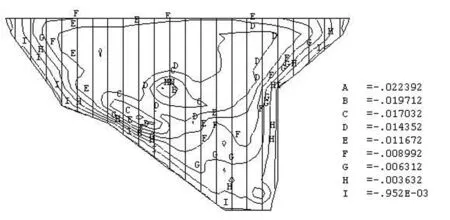
图9 面板挠度

在施工期，面板受外力作用主要是坝体自重，可以看出：面板在坝轴线方向的变形较小，向左、右最大位移分别为1.9cm和1.1cm。法向位移最大值2.28cm。挠度分布受河谷地形影响，最大挠度产生于左岸的面板位置处。施工期面板顺坡向应力均为压应力，最值3.84MPa，面板沿坝轴线方向均发生受拉现象，最值仅为0.42MPa，绝大部分面板受力仍为压应力。

考虑到文章篇幅和为了便于对比，将坝体蓄水期的结果以表2的形式给出：

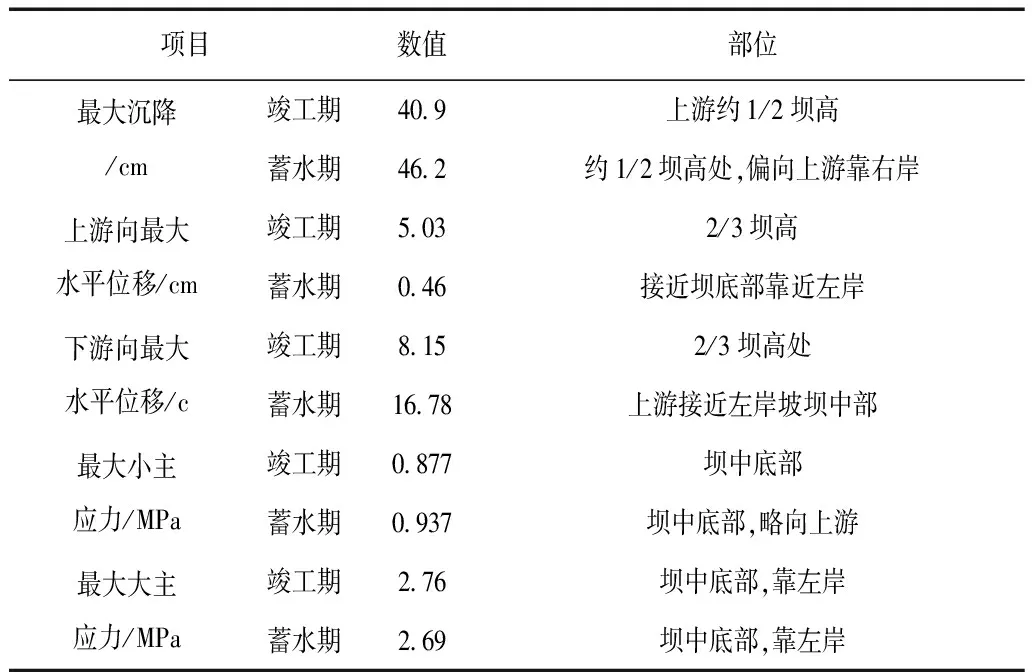
表2 不同工况坝体应力应变计算结果对比表

蓄水期从图中可得出：水荷载作用下，上游分区堆石体出现较大压缩变形，整个大坝的下游位移明显，表明水平位移的特征变化和基岩面的性态关系密切。坝体整体的沉降量均增大，但上游变化明显大于下游。大坝的应力值均比竣工期均偏大，最为明显的是坝体上游，下游影响较小。通过计算表格发现在水荷载作用下，小主应力变化明显比大主应力变化幅度大。

2.3.3 面板分析

面板应力应变计算成果见表3。

表3 面板结果对照表

面板蓄水期最大挠度大约在1/2坝高位置处，靠近面板中心。水平位移变化指向从两岸向河中央。轴向应力变化曲线表明面板中心受压，两岸周边缝附近受拉，大部分面板区域受到压应力，拉应力仅仅出现在岸边周边缝处。面板顺坡向应力表明面板主要承受压应力，周边缝附近位置处广泛存在，与轴向应力变化分析结果相同，这些拉应力区数值不大，但也应该引起重视。

由表可以得出：大坝内部各分区应力水平均偏低，面板应力变化与接缝变形均在设计要求和规范的允许范围内。

3 总 结

文章通过对堆石体材料的非线性特性进行分析的基础上，选取合适的数学模型对面板堆石坝进行有限元分析，结合工程实例计算出坝体和面板在不同工况下的应力变形情况，并对结果进行对比分析，认为坝体和面板的变形符合工程实测数据分布规律，该计算结果对此类工程的设计施工具有一定的参考作用。

[1]中华人民共和国电力部.DL/T5128-2001混凝土面板堆石坝施工规范[S].北京：中国电力出版社，2001.

[2]朱伯芳.有限元法原理与应用[M].北京：中国水利水电出版社，1998：10.

[3]曾以宁，屈智炯.土的非线性K-G模型研究[J].成都科技大学学报，1985(04)：143-149.

[4]迟守旭，庄小军.高混凝土面板坝压性垂直缝设计[J].山西建筑，2011，37(33)：208-209.

Finite Element Analysis of Stress Deformation for Concrete Slab Rock-fill Dam

HAN Xue

(Tonghe County Water Affairs Technology Service Center, Tonghe 150900, China)

In recent years, with the application of new ideas and new methods, the dam design level and modern construction level are progressive continuously, and the concrete slab rock-fill dam has been one of the most major dam style used widely. New technology applied in the slab rock-fill dam not only simplified the construction procedure but also guaranteed flood control over the dam. In combination with the project cases, this paper applied three-dimensional finite element calculation software to calculate the stress deformation layout law for dam body and slab during construction period and storage period, meanwhile, to analyze the slab characters as the time of slab design construction and operation management, the conclusion would bring a certain references for act project design and construction.

concrete; slab rock-fill dam; stress deformation; finite element; analysis

1007-7596(2017)06-0019-04

2017-05-20

韩雪(1968-)，女，黑龙江通河人，工程师。

TV641.43

B