岩体裂隙渗流区域非线性问题的数值求解分析

牟 宏，赵 巍

(大庆松嫩工程管理处，黑龙江 大庆 163311)

岩体裂隙渗流区域非线性问题的数值求解分析

牟 宏，赵 巍

(大庆松嫩工程管理处，黑龙江 大庆 163311)

防渗体系的构建一直是坝工设计中的重中之重，渗流分析是评价大坝安全稳定的主要指标之一，对渗流控制方案可行性和边坡抗滑稳定性的评价非常重要。由于渗流控制方程是线性的，通常无压渗流需指出渗流自由面的位置，而部分渗流区域边界的未知性和确定的必要性，使得连续介质的渗流分析转化为非线性问题。文章在三维裂隙网络渗流理论基础上，编制了求解非线性问题的相应程序，结合工程实例，通过对比数值模拟计算结果和工程实测结果，论证自编有限元程序的可行性。同时研究结果可以给类似工程设计提供一定的参考价值。

防渗体系；渗流控制；岩体裂隙；非线性问题；分析

0 前 言

渗流分析是大坝防渗设计的重要部分，在坝体出现安全事故中此方面是造成渗透破坏的重要原因之一[1]，问题在于对大坝的渗流分析考虑不全面。大坝渗流部位主要是坝体、边坡、基岩位置，还有许多由地下水运动、各类绕坝渗流等引起，这些渗流问题均是渗流区域的非线性问题，必须确定渗流自由面。自由面一般是可以随着降雨量和水位等外界因素的变化而变化，自由面上部为大气压。渗流区域非线性问题计算分析的重要环节是对渗流区域边界的确定，换言之是对渗流自由面和溢出面位置的确定，过程中确保迭代计算的稳定性。边界的确定是渗流分析研究的重要组成，同时渗流计算是评价大坝渗流安全稳定的主要指标，因此，对渗流区域非线性问题的正确求解以及分析研究具有重要的意义。

1 连续介质渗流非线性的渗透矩阵解析法

连续介质渗流区域求解中数学模型的确定主要是渗流方程的定解条件。连续介质渗流的非线性问题分为两种情形：饱和渗流和饱和-非饱和渗流，所以数学模型基于此分为两种。通常对于前者的二维非稳定流进行分析时，定解方程[2]以下4种：

1)Boussinesq方程式，原理是渗流自由面作为流量补给，看做水平面渗流的支撑方程，通常多用于在地下水运动的研究。

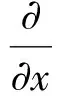
(1)

式中：H为地下水深；ε为为蒸发强度；ω为入渗强度。

2)Laplace方程式，渗流自由面当作流量补给，同时为下降流速条件，多用于结构稳定且不易压缩的堤坝。

(2)

3)扩散方程式，渗流自由面当作流量补给条件，基本假定是以杜布依为基础，故该方法多用于自由面变化程度小或者渗流坡降变化不大的土坝。

(3)

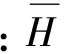
4)固结方程式，渗流自由面看成流量补给条件，对土体压缩性进行了定义，故多用于黏土筑坝的多种固结情形。

(4)

式中：sS为贮存系数。

在饱和-非饱和渗流分析中，常常使用Neuman方程式，此方程推导过程中不考虑渗流自由面的边界条件，做出特定假设后多用于非均质各向异性坝。所以该方程式转化式如下。

(5)

式中：C(ψ)为容水度；ψ为压力水头。

对于连续介质的非稳定渗流分析，渗流分布利用饱和渗流分析中的固结方程和自由面边界定解条件进行计算是符合实际的。

2 三维裂隙网络渗流自由面解析分析

多孔连续介质渗流分析主要是为了明确渗流的区域位置和边界条件，与裂隙岩体渗流分析的不同在于，不考虑岩块渗流的基础上，水流沿着裂隙方向流动，渗流也是基于此定向进行的。此时岩块主要承受水荷载，潜水面仅产生于裂隙处。因此，岩体裂隙渗流中渗流自由面是承压面和非连续的潜水面组合而成的曲面[3]。

2.1 潜水渗流自由面方程

岩体裂隙渗流分析的基本假定是岩块无渗透能力，水流只存在于岩体的裂隙网络中，各裂隙中水位高度的连接线组成的曲面定义为渗流自由面。故对各裂隙中水位的确定成为确定自由面的关键。此问题的研究原理类似连续介质渗流，确定水位这是一非线性问题，因为水位组成了岩体裂隙渗流的边界条件，同时满足既定位置上的水头高度和流量与外界渗出量的相同。假定裂隙岩体水流流态平稳，潜水自由面水量稳定，则渗流自由面各裂隙处端头水头差为零，即流量变化值为零。则潜水面边界方程见表达式(1)：

(6)

式中：Γ3为自由面边界；z为水流位置高度。

2.2 数值计算方法

在数值模拟分析计算时，定义面单元为裂隙单元，结点为裂隙之间的交叉点，在岩体三维裂隙网络渗流机理的基础上代入边界条件，即可得到各个结点上水头大小和流量值。

三维裂隙网络渗流数值模拟的基本单元采用的是二维渗流分析中的单元，本质上和连续介质二维渗流分析是相同的。对三维岩体裂隙网络渗流的非线性问题计算分析的过程如下：

1)网格划分整体的渗流区域，渗流计算第一步采用初始渗透系数作为整个渗流区域的渗透系数，然后建立整体渗透矩阵，在三维裂隙网络渗流原理基础上计算区域内各结点水头大小和流量值。

2)第一步求解出渗流场各结点水头值，与水流位置高度z进行比较，然后划分整个渗流区域为三个子区域R1、R2和R3。定义R1区域在渗流自由面上，R2区域在自由面下，R3区域为交错复合单元区。

3)给定子域R1的渗透单元渗透系数为K/1000；子域R2的渗透单元渗透系数与原始值保持一致。

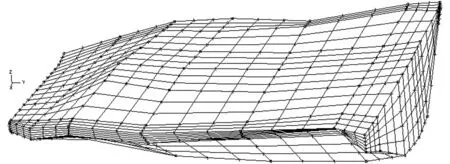
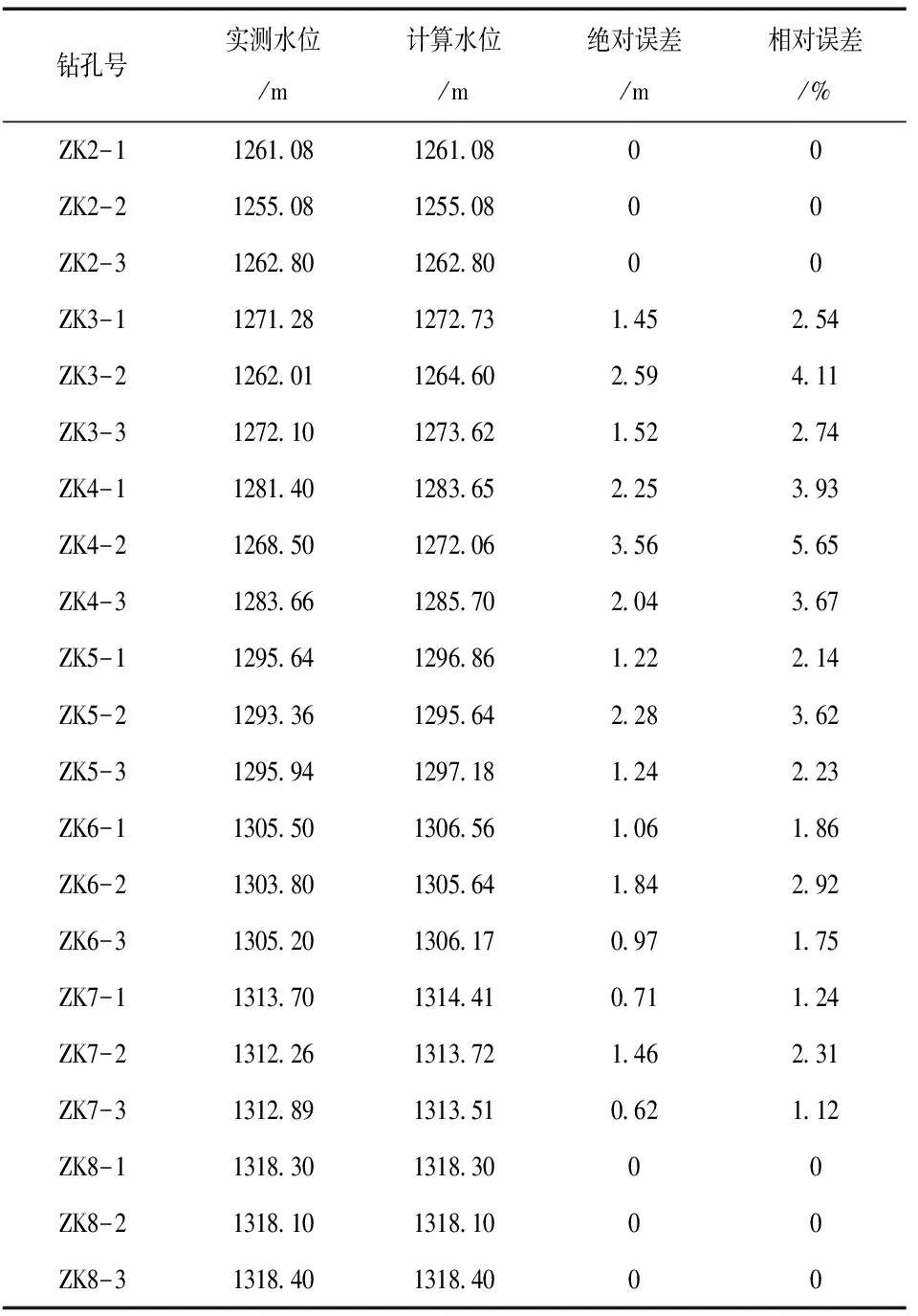
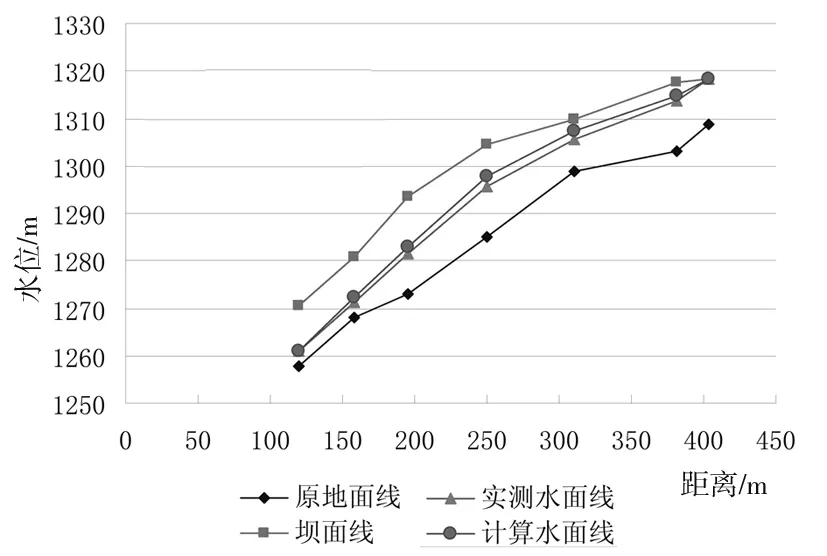
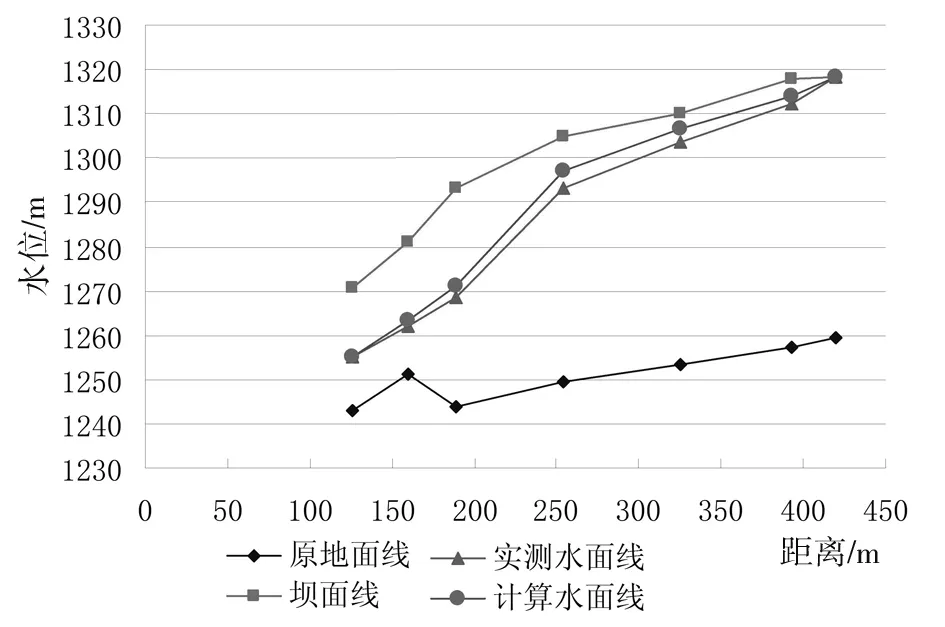
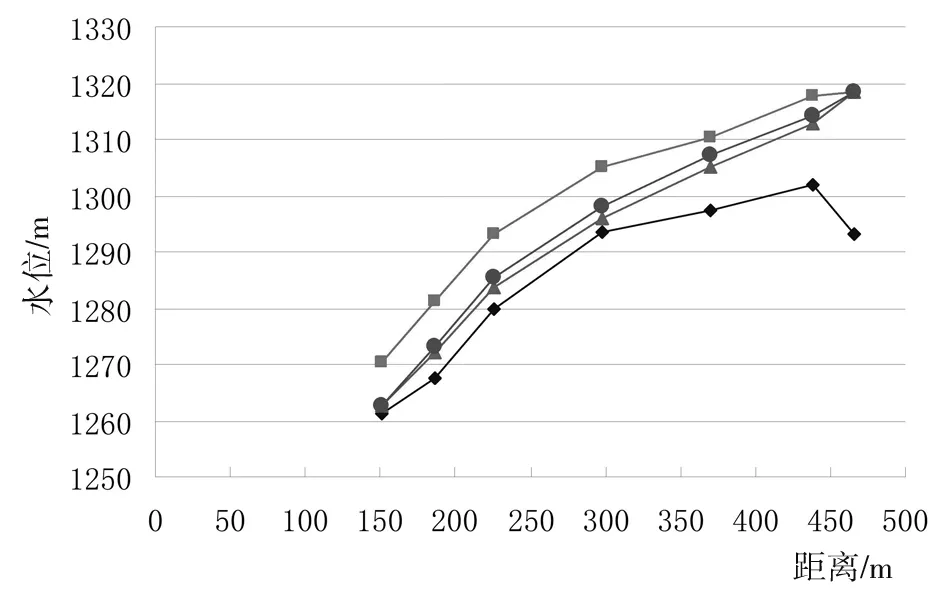
4)子域R3区域的复合单元，采用插值法逐个进行判断，通过对比分析高斯积分点的H和z计算结果，若H>z，则此高斯点认定为子域R2内，若H

5)对渗透矩阵进行重新组合，计算得出新的渗流场各个结点的水头大小和流量值。前提是以收敛准则为依据，判断精度要求，若满足，结束迭代过程；若精度不满足，重复运行过程(3)-(5)，最终使相邻两次迭代计算后的渗流自由面满足精度要求，此时可得出最终的渗流自由面位置。

3 工程实例

某尾矿库工程位于秦岭中部腹地山区，常年地貌是中高山侵蚀地貌。海拔位于1245-1948m之间，矿区地形南低北高，倾向为南西走向。矿区为一级支沟，沟长5.5km，底宽3-8m， “∨”型走向的河谷。初期坝和后期坝平面图见图1。工程防洪标准：初期校核洪水位为50-100a一遇；中、后期设计为200a一遇。河谷最大流量为160m3/h。工程所在库内布设坝面位移变形观测点3个，水位观测标尺5个，浸润线观测孔6个，定期观测并进行记录。

图1 初期坝和后期坝平面图

3.1 计算模型及网格划分

为更加符合工程实际观测，使得有限元计算结果和实际更加贴合，计算模型选取库区ZK2断面和ZK8断面之间的区域进行渗流分析。从上到下各断面的坝面线、浸润线、地面开挖线首尾相连形成三条曲线来进行计算分析。

尾矿库渗流数值模拟计算模型的建立的依据为ZK2-ZK8横断面图，计算区域是坝面线之下的大坝，区域不包括基岩下的覆盖层，计算模型的网格单元剖分图见2，采用软件ADINA进行的网格划分，模型中单元采用八结点六面体等参单元，总计剖分单元1628个，节点2174个。

图2 计算模型网格剖分

3.2 渗流计算参数与边界条件

渗流分析方法为有限单元法，ADINA建模后利用编制的SEEP程序进行计算。定义第一类水头边界为ZK2断面和ZK8断面的各自三个横断面，水头大小是各断面上的钻孔地下水位，其他表面均为第二类边界，通过第二类边界横断面上的各渗流量等于零。

考虑到现场试验渗透系数和实验室试验得出的渗透系数不同，渗流计算模型的渗透系数采用各大高校经反复演练并最佳拟合的物理参数，见表1。

表1 最佳拟合模型渗透系数

3.3 计算结果及分析

计算得出各钻孔计算水位和绝对误差如表2所示，(相对误差等于绝对误差和总水头的比值)。各截面浸润线实测值绘制的曲线图见图3-5所示。

表2 各钻孔计算水位及误差

图3 浸润面计算实测对比图(ZK2-1-ZK8-1)

图4 浸润面计算实测对比图(ZK2-2-ZK8-2)

图5 浸润面计算实测对比图(ZK2-3-ZK8-3)

综合各钻孔计算水位值和误差的对比分析，各横断面钻孔水位的实测值中间部位的计算误差明显>两边钻孔的水位值，工程实测结果中自由面上、下数值大、中间部位数值小，分布规律基本一致。实测值均<有限元计算出的各钻孔的计算水位值，采集点离钻孔ZK2和ZK8越近，误差越小，反之亦然。表格分析中最大相对误差5.68%，在允许范围内，表明该计算模型有限元分析计算结果中的浸润面位置虽比实测值偏高，但数值变化规律基本一致，直接验证了该计算程序的正确性和可行性。一定程度上说明，文章分析采用的最佳拟合模型和参照工程的各物理参数进行计算是正确的，符合工程实际。

5 结 论

文章基于连续介质非稳定渗流的原理，在渗流区域非线性问题的渗透矩阵和自由面三维裂隙网络渗流分析的基础上，利用有限元软件和自编程序对渗流区域非线性问题进行了研究，认为在应用单元渗透矩阵调整法时，对计算模型选取和区域边界条件的界定非常关键，特别在于渗流自由面的变化区域，有限元分析中的网格单元划分进行越密，则计算精度越高。通过计算结果和实测资料进行对比得出，认为采用该自编程序进行渗流区域非线性问题的求解是可行的。

[1]柴军瑞.岩土体水力学非线性问题[J].岩土力学，2003(24)：159-162.

[2]王均星，吴雅峰，白呈富.有自由面渗流分析的流形单元法[J].水电能源科学，2003，21(04)：23-25.

[3]梁业国，熊文林，周创兵.有自由面渗流分析的子单元法[J].水利学报，1997(08)：34-38.

Numerical Solution and Analysis for Nonlinear Problems about Rock-body Fissure Seepage Region

MU Hong and ZHAO Wei

(Daqing Songnen Project Management Administration, Daqing 163311, China)

Composition of the seepage protection system has been a priority for the dam project design and analysis of seepage is one of major index for evaluating the dam safety and stability, which is very important to evaluate the feasibility of seepage control scheme and slope stability against slip. Usually, the location of seepage free surface needs to be pointed out for unconfined seepage because the seepage control equation is linear, however, the unknown boundary of partial seepage region and necessity transforms the seepage analysis for continuous medium into the nonlinear problem. Based on the seepage theory of three-dimensional fissure net, this paper carried out a corresponding program to solve the nonlinear questions, combined with project cases, by comparing the calculated results with the observed results, it proves that the finite element grogram is feasible, simultaneously, the researched achievements may supply references for similar projects.

system of seepage protection; seepage control; fissure of rock body; nonlinear problem; analysis

1007-7596(2017)06-0006-04

2017-05-24

牟宏(1991-)，女，黑龙江大庆人，助理工程师；赵巍(1980-)，女，黑龙江大庆人，助理工程师。

TV

B