基于粗糙集的混合多属性目标威胁评估方法
2017-08-29刘静
刘 静
(山西国营大众机械厂,山西 太原 030024)
基于粗糙集的混合多属性目标威胁评估方法
刘 静
(山西国营大众机械厂,山西 太原 030024)
提出了一种基于粗糙集的混合多属性目标威胁评估方法。该方法根据水面舰艇防空作战中来袭目标的特点,确定影响威胁评估的各项指标,运用粗糙集理论确定评价指标权重,规避主观赋权的片面性,同时构造每个具体指标的效用函数。该方法提高了评估排序的合理性,算例表明该方法的可行性,为舰艇防空作战威胁评估提供了一条新的有效途径。
防空作战;粗糙集;威胁评估; 效用函数
现代防空作战的复杂性和不确定性日益凸显,为提高舰艇防空作战效能,混合多属性的威胁评估就显得十分必要。当前涉及空袭目标威胁评估的研究成果很多,如层次分析法[1]、核主成分[2]、灰色区间关联决策、贝叶斯网络和多属性决策法[6]等。
效用函数[3,4]通常用来表示消费者从消费既定商品组合中所获得满足的程度。现将效用函数概念扩展表示决策者在决策中所获得的效用与决策中各指标权重数量关系的函数,反映指标对于完成目标的贡献。
本文根据水面舰艇防空作战中来袭目标的特点,确定影响防空威胁评估的各项指标,并对其进行量化计算,同时引入粗糙集的粗糙依赖度计算评价指标权重,最后利用构造出的每个具体指标的效用函数进行威胁评估排序,即一种基于粗糙集的混合多属性目标威胁评估排序方法。
1 经典威胁评估模型
威胁评估是为确定敌方武器装备、兵力结构部署等对我方形成威胁的程度或等级。由此建立威胁评估的三级功能模型,如图1所示。

图1 威胁评估三级功能模型
由图1可知我方受到的总威胁程度为:
T=k·(w1·E+w2·I+w3·P).
(1)
式中,k为威胁修正系数;w1,w2,w3分别为敌方作战能力、敌方作战意图、敌方作战机会的权重,E、I、P为对应的量化值。
2 量化威胁指标[2]
影响防空威胁评估的指标很多,一般情况下考虑目标类型、目标距离、目标高度、目标速度和目标攻击角等因素。这些因素既有定量描述,又有定性描述,且相互关系较复杂,因此需要对上述因素进行综合评估。
2.1 目标距离
目标距离隶属度函数可表示为:
(2)
式中,D1=30 km,D2=300 km,kd=10-2。
2.2 目标速度
速度隶属度函数可表示为:
y(v)=1-exp(αv).
(3)
式中,v>0,单位为Ma;α=3×10-3×340=-1.02。
2.3 目标高度
对战机和反舰导弹而言,大都采用超低空突防的方式提高突防成功的概率。目标高度隶属度函数可表示为:
(4)
式中,a=0.05 km,kh=2×10-2。
2.4 目标舷角
目标舷角威胁隶属度函数表示为:
y(θ)=exp(-kθθ2),-90°≤θ≤90°.
(5)
式中,kθ=3.5×(π/180)2。
2.5 目标类型
根据既有的应用实例,量化常见空袭目标类型为{弹道反舰导弹、飞航反舰导弹、轰战机(攻击机)群、战斗机群、轰炸机、战斗机(攻击机)、电子战飞机、预警机、其他飞机},对应的威胁度量化值为{1,0.9,0.8,0.7,0.6,0.5,0.3,0.2,0.1}。
3 基于粗糙集的混合多属性目标威胁指标权重计算方法
粗糙集理论目前已广泛应用于解决不确定、不精确和不完全数据的多属性决策问题。
基于粗糙集的混合多属性目标威胁指数权重的计算步骤[5]如下:
步骤1:获取原始数据矩阵,构建决策信息系统。对于空中目标混合多属性决策问题,目标集T=(T1,T2,…,Tm)T,目标因素属性U=(U1,U2,…,Un)T,指标的权重向量为W=(W1,W2,…,Wn)T。
步骤2:计算指标ck的posc-ck(D)。
步骤3:计算指标ck关于D的重要性sig(ck)。
步骤4:归一化ck的重要性,得到ck的权重wk。
4 基于粗糙集的混合多属性目标威胁评估方法
1) 计算隶属度
根据原始数据,计算各个指标的隶属度函数,对所得数据进行归一化处理,得到n项指标,m个样本(m>n),即矩阵X;
2) 标准化处理

(6)
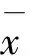
3) 计算威胁指数权重
将标准化后的矩阵X*定义为决策矩阵H。按照3中的步骤计算出目标威胁指数权重。
4) 构造效用函数
定量指标中,距离、高度、目标舷角属于成本指标,即指标值越小,威胁程度越高;而速度、目标类别属于效益型指标,即指标值越大,威胁程度越高。进行威胁评估前,需要规范化处理定量和定性指标,得到[0,1]范围内的各指标值的函数值。
构造效用函数,首先采用确定当量法找出效用值为0.5的结果值,其余效用按照比例内插法得到。方案Pi的成本指标的效用函数为
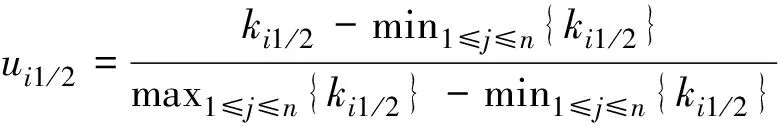
i=1,2,…,n
(7)
式中,max1≤j≤n{ki1/2}表示成本指标的最大值,min1≤j≤n{ki1/2}表示成本指标的最小值。

(8)
式中,max1≤j≤n{kj3/4/5}表示效益指标的最大值,min1≤j≤n{kj3/4/5}表示效益指标的最小值。
由上述各式可得到优选方案Pi的综合量化值Ei=W·ui=W·(ui1,ui2,ui3,ui4ui5)T,i=1,2,3,…,n
(9)
比较上述综合量化值Ei可得最大评估值。
5 实例应用
根据信息系统采集到的5批空中目标,经信息检测和相关综合等多级处理得到空袭目标威胁评估指标如表1所示。经量化评估后得到各指标的隶属度如表2所示。
运用粗糙集算出评估指数权重向量W=(0.646,0.124,0.0109,0.071,0.050)T。
由式(7)~(8)算得效用函数向量,由式(9)可得E1=0.68,E2=0.294,E3=0.911,E4=0.489,E5=0.078,故得到威胁评估的结果T3>T1>T4>T2>T5。
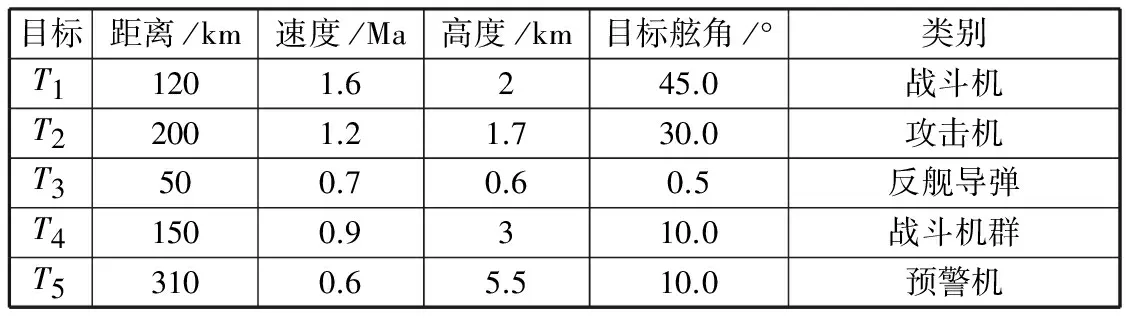
表1 空袭目标威胁评估指标
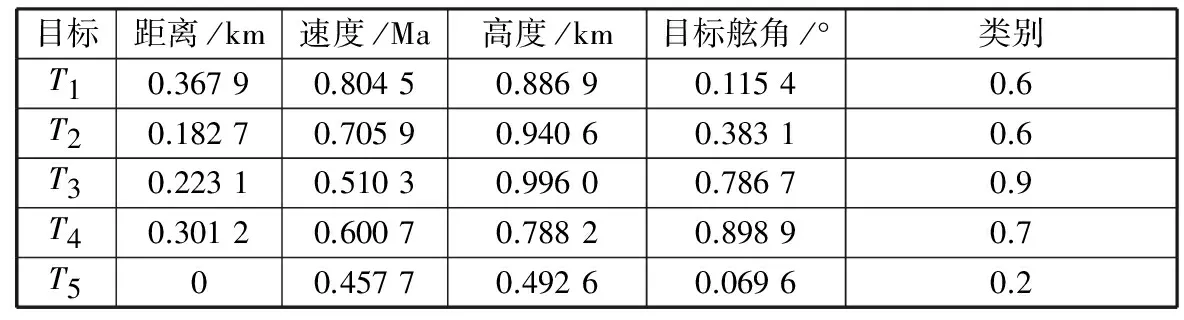
表2 各评估指标量化得到的威胁隶属度
6 结论
本文基于水面舰艇防空作战中来袭目标的特点,在效用函数的基础上引入粗糙集的权重赋值方法,克服了单一方法的片面性,提高了评估排序的合理性,可以更好地辅助指挥信息系统的辅助决策。
[1] 闫冲冲,郝永生.基于层次分析法(AHP)的空中目标威胁度估计[J].计算技术与自动化,2011,30(2):118-121.
[2] 陈维义,王少蕾,周菲.基于加权核主成分TOPSIS方法的舰艇防空威胁评估[J].海军工程大学学报,2014,26(1)87-91.
[3] 李保明,刘家壮.效用函数与纳什均衡[J].经济数学,2000,17(4):21-28.
[4] 宋亚楠,仲茜,刘斌.基于边际效用函数的网络资源调度[J].电子学报,2013,41(4):632-638.
[5] 李远远,云俊.粗糙集理论在综合评价中的应用研究[J].中国管理科学,2009(17)(专辑):192-196.
[6] 曲长文,何友,马强.应用多属性决策的威胁评估方法[J].系统工程与电子技术,2000,22(5):26-29.
A Hybrid Multi-attribute Target Threat Assessment Method Based on Rough Set
Liu Jing
(State-ownedDazhongMachineryPlant,TaiyuanShanxi030024,China)
A hybrid multi-attribute target threat assessment method based on rough set is proposed. Aiming at the characteristics of air-raid targets in air defense operations of surface ships, the threat assessment indexes of air defense operations are determined and quantified. The RS theory is applied to compute the weight coefficient. At the same time the utility function of each specific index is constructed, then improves the rationality of ranking. The feasibility of the method is verified by an example and provides an effective new approach to the threat assessment of air targets in air defense operations of surface ships.
air defense operation; rough set; threat assessment; utility function
2017-06-29
刘 静(1979- ),女,河北景县人,硕士,主要研究领域为智能控制、故障诊断。
1674- 4578(2017)04- 0044- 02
TP18,TP206
A
