基于全变差与非局部正则化的CS重建算法研究
2017-08-29孙铁强韩亚楠
孙铁强,韩亚楠
(华北理工大学信息学院,河北唐山063000)
基于全变差与非局部正则化的CS重建算法研究
孙铁强,韩亚楠
(华北理工大学信息学院,河北唐山063000)
压缩感知(Compressed sensing,CS)理论突破了传统奈奎斯特采样定理对信号带宽的限制,实现了从少量的观测值中精确重建原始图像。结合图像的非局部相似性及其在某种变换域的稀疏性的先验知识,提出了基于全变差与非局部正则化的压缩感知核磁图像重建算法。在该算法的求解过程中,用光滑且非凸函数logdet()代替秩,而不是传统的核范数,然后使用增广拉格朗日法,将函数的约束问题转化为非受限优化问题,通过交替极小化思想对优化问题进行求解,大大降低算法的复杂度。仿真结果表明,与传统的重建方法或TV约束重建方法相比,算法能够更好地提高重建核磁图像的峰值信噪比和视觉效果。
压缩感知;非局部相似性;全变差;图像重建
1 概述
压缩感知理论(Compressive Sensing,CS)理论[1,2]是由Dono⁃ho、Candes和Tao等人在2006年提出的一种新颖的采样理论。其主要内容是少量随机线性投影的可压缩或者稀疏信号包含了重建原始图像所需要的足够信息。实现了信号在采样速率远低于奈奎斯特采样定理要求的采样速率的情况下,完成信号的精确重建。压缩感知理论的数学模型表示如下:设图像信号为x∈RN,稀疏基为:ϕ∈[ ] ϕ1,ϕ2,…ϕN,图像信号表示为:

信号x在变换基ϕ仅有k个基线性表示,且k< 上式中,Α为传感矩阵,φ为观测矩阵,φ必须满足约束等距性: 信号x具有稀疏性,且测量矩阵满足约束等距性[3],则可将问题转化为下列所示的非线性优化问题,求解最小的l0范数,最后由测量值y实现对原信号的精确重建,如下所示: 压缩感知重建算法作为压缩感知理论的核心问题之一,直接关系到高维图像信号在实际中应用的成败,所以一直是该领域的研究热点。传统的CS重建算法基于图像在某一变换域的先验知识[4],通过求解特定的优化问题,实现对信号的重建。基于图像潜在先验知识许多学者先后提出小波阈值去噪法[5]、全变差去噪法[6]、奇异普分析去噪法[7]等。最具代表性是TV模型,利用稀疏图像的梯度属性,将全变差作为正则项[8]的图像重建算法,在图像去噪方面取得了很好的效果;近年来基于非局部相似模型的提出获得极大的关注,根据图像具有的自相似性质,Buades等[9]的非局部均值算法的提出,在有效保持图像纹理细节的同时是抑制图像噪声。本文在利用图像低秩属性的同时,引入稀疏性先验,同时考虑图像的局部信息和非局部信息,提出基于全变差与非局部正则化的图像压缩感知重建算法,并给出相应的求解算法,实现在相同的采样数据下,进一步提高图像的重建精度。 图像的非局部相似性即:自然图像内部的不同位置呈现出的形态结构相似的图像块,这种相似结构即使是在图像的边缘区域或纹理较丰富的区域也仍然广泛存在。在压缩感知图像重建算法的研究中,利用图像本身的自相似结构的先验知识,可以极大改善重建图像的质量。 在非局部相似块组的构建中,采用如下匹配算法[10]。假设估计图像首先从̂中得到n个样本小块表示位置i处的参考块,其大小为(例:6×6,d=36),以x̂i为中心在其周围范围寻找与它最相似的m个小块,块与块之间的相似度可用欧氏距离度量: 其中,T是事先定义的经验阈值;Gi表示收集到的所有相似块位置的集合;将每个相似块转为列向量并按其与参考块相似度大小排列,可得的相似块组其中组中每个块的结构相似性使得Xi是一个具有低秩特性的矩阵。事实上,Xi通常会被噪声污染,使得低秩约束产生偏差。所以,通常将矩阵Xi表示为Xi=Li+Wi,Li和Wi分别表示低秩矩阵和高斯噪声矩阵。低秩矩阵Li的求解可以表示为如下的优化问题得到: 其中ε表示一个很小的常数,函数E(X,ε)表示奇异值的对数和,所以函数E(X,ε)是一个光滑的非凸函数。文献[13]替代函数E(X,ε)可以实现比核范数更好的逼近秩。对于既不是方的也不是对称正定的矩阵Li∈Cn×m,n 在基于压缩感知的图像重建算法中,先验知识的使用能够极大提高重建图像的质量[14]。由于图像信号的复杂多变,目前的重建图像大都基于单一的稀疏先验,难以精确的保持图像的局部精细结构。本文结合图像的非局部相似性先验和全变差的稀疏先验,提出一种改进压缩感知的图像重建算法。假设图像的向量形式x∈Rn,Φ为测量矩阵,测量值为y重建模型如下: 其中y为图像x的初始采样,TV(x)代表图像x的全变差约束项。表示对每个样本邻域内取相似块xi的集合。L(Li,ε)为秩函数的替代。 其中D1和D2分别为二维图像水平和垂直方向的梯度算子。对于上述的重建模型,我们可以利用ADMM算法[15]的思想,通过交替极小化整个图像的x和低秩矩阵Li进行求解。也就是先固定一个值,对另一个值进行极小化求解,同理对其另外一个值求解,这样交替进行直到算法收敛结束。 首先对所求图像求一个初始估计值,然后对图像的每个像素l取相应的样本块xi,同时取每个样本块xi的相似块集合。然后,可以通过下面的极小化问题求解每一个Li: 其中,σ()k是第k步解,所以可以用如下的迭代方程求解: 其中,UξV是Xi的SVD分解形式,由于权重阈值是局部极小值,使得总体目标函数值下降。在文献[17]加权l1范数在逼近l0范数方面,具有更好的重建效果。当Li为向量时,非凸函数logdet()就是我们所熟知的加权l1范数,在文献[13]的仿真结果表明,在基于压缩感知的图像重建方面,logdet()比核范数具有更好的重建效果。 通过求解每个Li后,可以通过求解下面的最优化问题来求解整个图像: 上式直接求解,含有大量的矩阵求逆运算,计算量大,因此通常不会直接求解。在实际应用中,将上述方程分解成两个子问题分别进行求解。引入辅助变量可得: 其中,z∈CN是辅助变量,β是一个正标量,μ∈CN是拉格朗日乘子。令g=Dlx,则优化方程的迭代如下: ρ为一个常数,对于固定的x(l),μ(l)以及β(l),可得z()l+1的如下形式: 对角矩阵的值代表了覆盖这个像素位置的像素块的个数,每一项代表一个像素的位置。是一个对角矩阵,其中表示块平均值,通过寻找每个样本块的相似小块,求出相似小块平均值,所以(21)式可以通过如下形式简单求解。 通过对(19)的低秩矩阵Li的不断更新,获得一个未知图像的初步估计。之后用更新的低秩矩阵Li通过方程(20)迭代计算出x,这个过程一直迭代,到算法的最后收敛。 为了便于评价和对比3种MRI图像重建算法的性能,对此,本文将引入峰值信噪比(Peak Signal to Noise Ratio,简称PSNR)和相对误差两个指标对本文算法进行客观评价。峰值信噪比是指信号最大可能功率和影响其表示精度的破坏性噪声功率之比。可以反映重构图像质量。由于许多信号都有非常宽的动态范围,因此常用对数分贝(dB)为单位来表示。相对误差是指重建图像所造成的误差与原始图像之比。定义如下: 上式中n×n表示图像大小,MAXX代表图像中最大像素值。x̑,x分别代表重建图像和原始图像。PSNR越大,表示重建后的图像与原始图像越接近[16]。 图1 30%测量率下脑部扫描图1的重建结果 图1和图2分别给出了在相同采样数据量下,传统的重建算法,加权TV算法和本文重建算法的重建结果。本章算法重建后的图像PSNR较大且相对误差较小,有效的保留了图片的细节和轮廓;而LBP算法和加权TV算法重建结果呈现出较大伪影,有较明显的细节丢失,视觉效果差。由此,可以看出本文算法的重建结果更接近原始图像。 本文在图像自身稀疏先验的基础之上,利用图像的邻域结构信息,把图像的非局部相似性作为额外先验知识应用于压缩感知重建算法进行约束,并给出了最终的优化重建模型以及相应的优化求解算法。由仿真结果分析可知,在相同的采样率的情况下,使用本文算法重建图像的无论是视觉效果,还是峰值信噪比和相对误差都比传统的图像重建算法(LBP)和加权TV算法要好。由此可见,本文算法用于磁共振图像重建精确度较高,值的进一步研究。 图2 30%测量率下脑部扫描图2的重建结果 表1 30%测量率下MR图像重建结果的相对误差和PSNR [1]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306. [2]Candès E J,Tao T.Near-optimal signal recovery from random projections:universal encoding strategies?[J].IEEE Transactions on Information Theory,2006,52(12):5406-5425. [3]Candès EJ,Wakin MB,Boyd S.Enhancing Sparsity by Reweight⁃edl1Minimization[J].Journal of Fourier Analysis and Applica⁃tions,2008,14(5):877-905. [4]Qaisar S,Bilal R M,Iqbal W,Naureen M,Sungyoung L.Com⁃pressive sensing:from theory to applications,a survey.Journal of Communications and Networks,2013,15(5):443−456. [5]Bioucas D J M,Figueiredo M A T.A new TwIST:two-step it⁃erative shrinkage thresholding algorithms for image restora⁃tion.IEEE Transactions on Image Processing,2007,16(12):2992−3004. [6]Rudin L,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms.Physica D,1992,60(1−4):259−268. [7]Luo J H,Li W Q,Zhu Y M.Reconstruction from limited-an⁃gle projections Based on δ-u spectrum analysis.IEEE Trans⁃actions on Image Processing,2010,19(1):31−140. [8]Chambolle A,Lions P L.Image recovery via total varia-tion minimization and related problems.Numerische Math-ematik, 1997,76(2):167−188. [9]Buades A,Coll B,Morel J M.A non-local algorithm for image denoising.In:Proceedings of the 2005 Computer Vi-sion and Pattern Recognition(CVPR).San Francisco,CA:IEEE,2005. 60−65. [10]DABOV K,FOI A,KATKOVNIK V,et al.Image denoising by sparse 3-D transform-domain collaborative filtering[J].IEEE trans-actions on image processing,2007,16(8):2080-2095. [11]CAI J,CANDES E,SHEN Z et al.A singular value threshold⁃ing algorithm for matrix completion[J].SIAM journal of optimi⁃zation,2010,20(4):1956-1982. [12]M.Fazel,H.Hindi,and S.Boyd,”Log-Det heuristic for matrix rank minimization with applications to hankel and euclidean distance matri-ces,”in Proc.of Am.Control Conf.,pp.2156-2162,2003. [13]Weisheng Dong,Guangming Shi,Xin Li,Yi Ma and Feng Huang.”Com-pressive Sensing via Nonlocal Low-Rank Regu⁃larization.”IEEE Transac-tions on Image Processing A Publi⁃cation of the IEEE Signal Processing Society.2014,23(8):3618-3632. [14]Qaisar S,Bilal R M,Iqbal W,Naureen M,Sungyoung L.Com⁃pressive sensing:from theory to applications,a survey.Journal of Communications and Networks,2013,15(5):443−456. [15]D.Goldfarb and S.Ma.Fast multiple splitting algorithms for convex optimization.Arxiv preprint arXiv:0912.4570,2009. [16]Liu H Y,Wei Z H,Zhang Z R.Improved kernel regression model for image restoration[J].Journal of Image and Graphics, 2011,16(12):2140-2144. [17]E.Candes,M.Wakin,and S.Boyd,”Enhancing sparsity by reweighted l1 minimization,”Journal of Fourier Analysis and Applications,vol.14,no.5,pp.877-905,2008. Research on CS Reconstruction Algorithm Based on Total Variation and Nonlocal Regularization SUN Tie-qiang,HAN Ya-nan The Compressed sensing(CS)theory breaks through the limitation of the traditional Nyquist sampling theorem to the signal bandwidth,and realizes the accurate reconstruction of the original image from a small number of observations.Based on the non-local similarity of image and its a priori knowledge of sparsity in a certain transform domain,a new method of compres⁃sion-aware magnetic image reconstruction Based on total variation and non-local regularization is proposed.In the process of solving the algorithm,the smooth and non-convex functionlogdet()is used instead of the rank rather than the traditional ker⁃nel norm,and then the Augmented Lagrangian method is used to convert the constraint problem of the function into an unre⁃stricted optimization problem.Minimize the idea of solving the optimization problem,greatly reducing the complexity of the al⁃gorithm.The simulation results show that compared with the traditional reconstruction method or TV constraint reconstruction method,this algorithm can improve the peak signal-to-noise ratio and visual effect of reconstructed NMR image. Compressed sensing non-local similarity total variation Image reconstruction TP18 A 1009-3044(2017)21-0199-04 2017-06-25


2 非局部相似模型




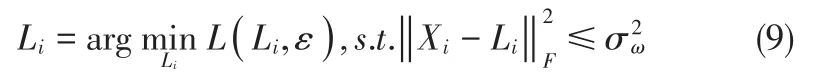
3 本文压缩感知图像重建







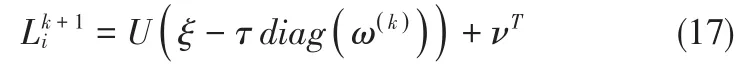





4 实验仿真及结果分析
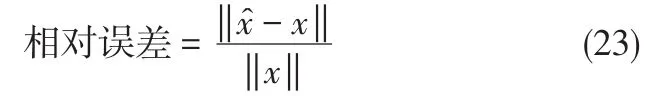


5 结束语


(North China University of Science and Technology,Information Institute,Tanshan 063000,China)
