电子设备橡胶隔振器静动态特性分析方法研究
2017-08-28王志海
李 钊,彭 超,王志海
(中国电子科技集团公司第三十八研究所国家级工业设计中心, 安徽 合肥 230088)
电子设备橡胶隔振器静动态特性分析方法研究
李 钊,彭 超,王志海
(中国电子科技集团公司第三十八研究所国家级工业设计中心, 安徽 合肥 230088)
橡胶隔振器采用粘弹性阻尼材料进行振动、冲击防护与控制,传统做法是依靠大量的经验公式和试验数据进行试错设计,效率低,成本高。文中针对电子设备中橡胶隔振器的静动态特性分析方法问题,系统建立了一套基于非线性有限元方法的求解策略。以某型橡胶隔振器为例,获得了其静刚度、蠕变和松弛特性等静态特性以及迟滞回环、谐响应和冲击响应等动态特性,并对橡胶隔振器设计和选型中的2个关键参数(橡胶超弹性和匹配质量)进行了讨论,可供橡胶隔振器设计方法研究参考。
橡胶隔振器;静刚度;动刚度;振动;冲击
引 言
随着电子设备不断向集成化、一体化和模块化方向发展,关键元器件或模块在宽频振动和高冲击力学环境下的结构可靠性是设计师面临的亟需解决的工程技术问题[1]。橡胶隔振器采用粘弹性阻尼材料进行振动、冲击防护与控制[2],具有结构紧凑、可设计性强、工艺性好、成本低廉等优点,广泛应用于电子、汽车、船舶和建筑等工程领域。橡胶隔振器的基本特性包括静态特性和动态特性[3-6]。静态特性以静刚度为基本指标,主要满足隔振系统的位移控制要求,广义上还包括隔振器长期存放或使用时静刚度发生偏移的蠕变或松弛特性;动态特性主要以动刚度和减振效率为基本指标,主要满足隔振系统的振动冲击控制要求,包括迟滞特性、谐响应特性和冲击特性等。由于橡胶材料和减振结构的复杂性,传统做法是依靠大量的经验公式和试验数据进行试错设计,通过反复设计、加工、试验、更改等不断改进设计方案,效率低,成本高。随着非线性有限元理论和计算机求解效率的不断提高,利用数值方法求解橡胶隔振器的力学特性逐渐发展起来[7-9],并为电子设备中橡胶隔振器的选型、设计和可靠性分析提供了重要参考。
本文针对某机载电子设备中橡胶隔振器的静动态特性分析方法进行了研究。首先建立了考虑橡胶超弹性和粘弹性的有限元分析模型;然后分析了橡胶隔振器的静刚度以及在蠕变和松弛现象中的静刚度偏移曲线,获取橡胶隔振器在动态载荷环境下的迟滞特性、谐响应特性和冲击特性等;最后对橡胶隔振器中的一些关键参数进行了数值考评,为橡胶隔振器的基本设计方法提供了重要参考。
1 有限元分析模型
本文以机载电子设备中某关键元器件所采用的橡胶隔振器为分析对象。该橡胶隔振器为平板式隔振器,结构紧凑、安装空间小、有防冲凸缘,如图1所示。它包括铝材安装板、橡胶减振结构以及内圈3部分。铝材安装板与电子设备基础安装位置通过4个螺栓孔相连,内圈位于橡胶结构的中心孔处,隔振元器件与内圈通过螺栓连接。
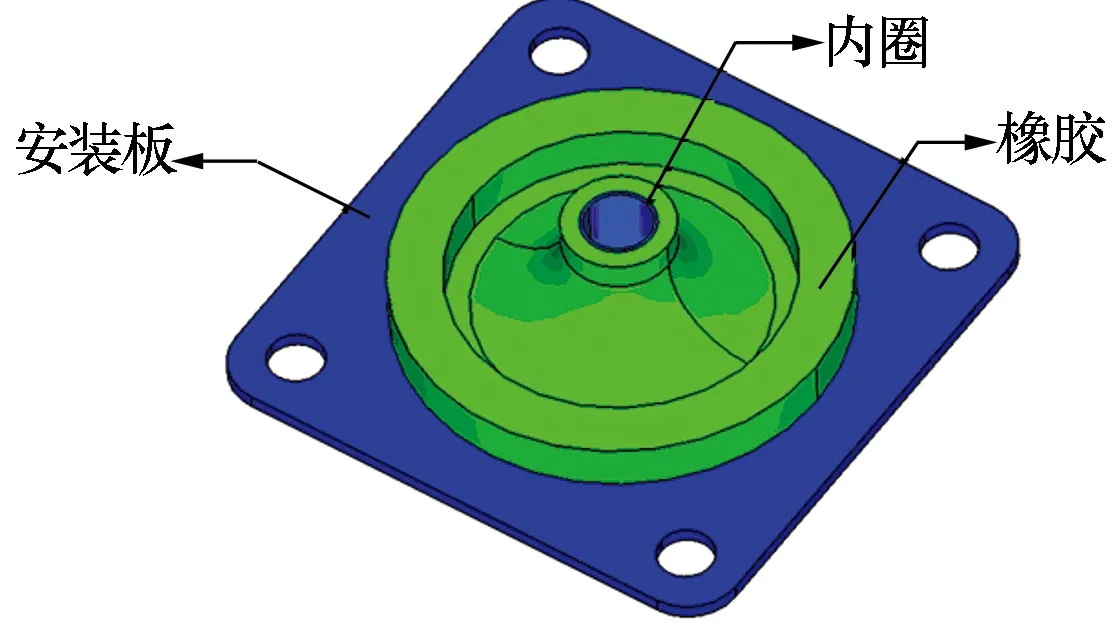
图1 橡胶隔振器结构示意图
根据橡胶隔振器的具体结构形式,建立有限元模型,如图2所示。建模中进行一定的简化,去除对结构力学性能影响较小的倒角、小螺纹等结构。铝材安装板、橡胶减振结构以及内圈均采用实体单元进行模拟,且绝大部分单元为具有较高网格质量的六面体单元,以提高求解精度,并降低计算时间;隔振元器件采用质量单元进行等效,设为公称负荷0.25 kg;质量单元与内圈通过刚性单元连接。橡胶减振结构和内圈沿周向划分为60个等份,整个分析模型共包含25 844个单元,29 714个节点。橡胶隔振器中的铝材安装板和内圈采用经典线弹性材料进行模拟,而橡胶减振结构由于高分子聚合物材料力学行为较为复杂,因此与常规的金属材料差异较大,通常表现为具有大变形特征的超弹性和具有动态阻尼特性的粘弹性,这也正是决定橡胶隔振器的静动态特性的关键因素。
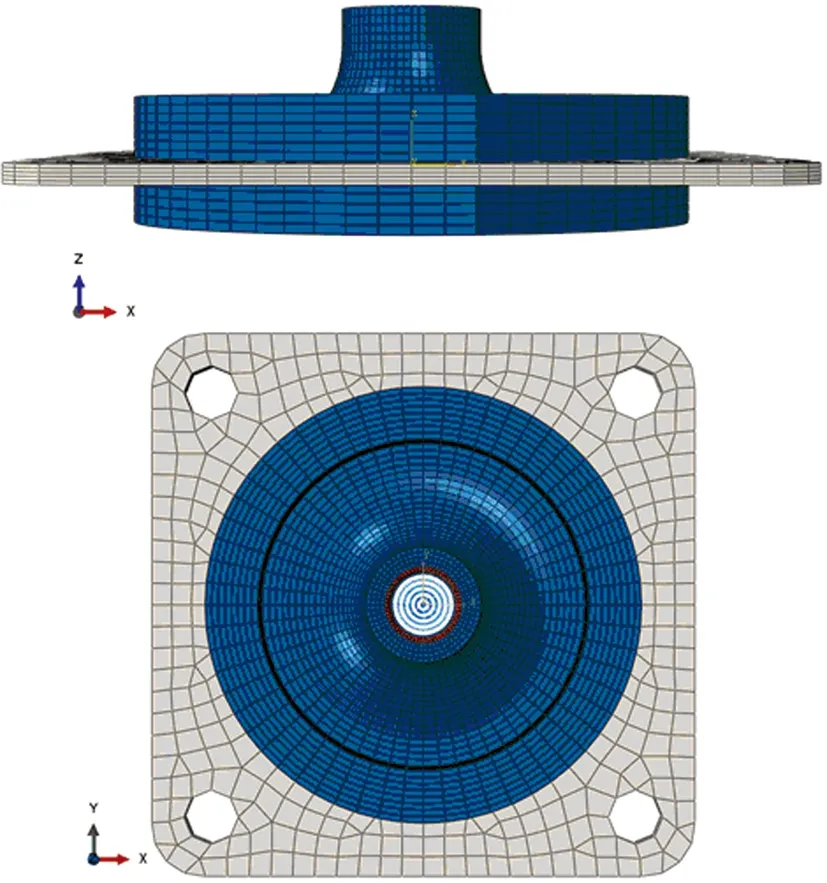
图2 橡胶隔振器网格模型
目前描述橡胶超弹性的本构模型主要分为2种,分别为唯象模型和统计热力学模型[3]。在工程有限元计算中常用到的模型为唯象本构模型,它从连续介质力学出发,假设橡胶材料的变形为各向同性的超弹性体均匀变形,将应变能密度函数表示成关于3个应变不变量(主伸长率或变形张量)的函数,主要有Mooney-Rivlin模型、Yeoh模型、Neo-Hooke模型及Ogden模型等。本文采用具有三次应变能函数的Yeoh模型:
U=C10(I1-3)+C20(I1-3)2+C30(I1-3)3
(1)
式中:U为橡胶材料应变能函数;I1为Cauchy-Green应变张量的第一不变量;C10、C20和C30为材料参数。
Yeoh模型中的材料参数可由简单变形实验数据拟合得到,并且可以用来预测其他变形的力学行为,描述的变形范围也较宽。材料参数选用由具有较高测试精度的自动网格法测得的试验结果。橡胶材料具有近乎不可压缩的特性,泊松比一般在0.5左右,采用常压力杂交三维实体单元C3D8H和C3D6H。
橡胶材料的粘弹性主要与激振频率和振幅相关[4],其中激振振幅相关性主要是由橡胶填充结构的断裂和重构引起的,较为复杂,这里暂不作考虑。在橡胶材料的频率相关性的研究中,采用的材料粘弹性本构模型主要有复常数模量模型、分数指数模型、微振子模型、标准流变学模型和分数导数模型等。目前主要采用基于各向同性假设的扩展Maxwell模型。该模型可以在较宽的频段内对橡胶材料的动态特性进行拟合,相关Prony级数参数可以通过动态试验获得,这里采用文献[4]给出的结果。
2 非线性问题求解策略
非线性问题求解按分析方法的不同分为隐式算法和显式算法两类[10]。隐式算法通过组合增量和迭代过程,增量地施加给定的载荷,逐步获得最终解答,适合求解静力学和一般动力学问题;显式算法则从上一个增量步前推出当前的动力学状态,无需进行迭代,但为了保持数值的可靠性和稳定性,必须采用很小的稳定时间增量(通过试算,本文所建模型的稳定时间增量约为9.49 × 10-8s),因此增量步数通常较隐式算法大几个数量级,一般用于求解高速动力学事件。此外,橡胶材料具有超粘弹性的高度非线性特征,无法采用传统上用于求解线性动力学的模态叠加法。基于以上原则,确定了如下橡胶隔振器静动态特性的求解策略:
1)橡胶隔振器静态问题采用隐式静态求解算法,安装孔处全部固定约束,在隔振元器件上分别沿轴向和径向施加位移边界条件,并定义橡胶可能产生接触的自接触关系,通过模拟得到的安装孔处的支反力可获得橡胶隔振器的静刚度;
2)橡胶隔振器蠕变和应力松弛问题先通过隐式静态求解算法获得橡胶隔振器静态解,而后保持载荷或位移边界不变,采用隐式准静态求解算法获得频率相关橡胶材料的时间响应;
3)橡胶隔振器迟滞问题采用隐式直接动力学分析算法,安装孔处全部固定约束,在隔振元器件上施加周期性位移边界条件,通过模拟得到的安装孔处的支反力以及隔振元器件的位移响应可获得橡胶隔振器的迟滞曲线;
4)橡胶隔振器谐响应问题采用隐式直接解法的稳态动力学算法,在安装孔处施加频域谐响应位移边界条件,通过模拟得到的隔振元器件处的位移响应可获得橡胶隔振器的频域减振特性;
5)橡胶隔振器冲击问题采用隐式直接动力学分析算法,在安装孔处施加冲击加速度条件,通过模拟得到的隔振元器件位移响应可获得橡胶隔振器的冲击曲线。
3 橡胶隔振器静态特性
图3为模拟得到的橡胶隔振器在轴向和径向的静态特性曲线。可以看出,它具有显著的非线性特征,呈现出与橡胶超弹性材料特性一致的S型。橡胶隔振器轴向和纵向的静刚度相近,且在小变形范围内径向刚度高于纵向刚度。在2个方向的静态加载中,橡胶材料的最大应变均在60%以上(如图4所示),且橡胶隔振器在径向位移加载至4.5 mm时发生了自接触,非线性计算由于复杂的局部接触变形情况在径向位移加载至7.5 mm时中止。
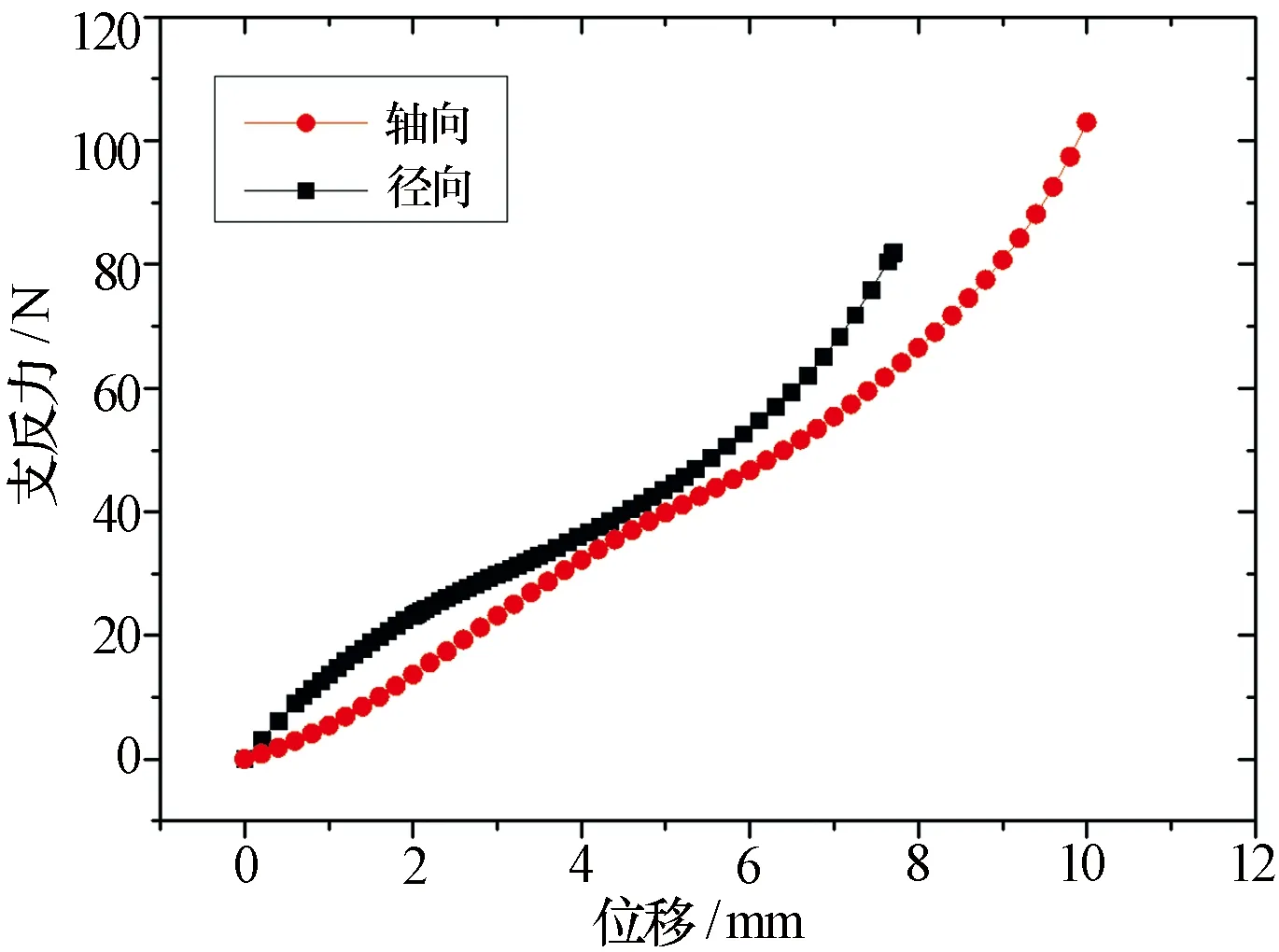
图3 橡胶隔振器静态特性曲线
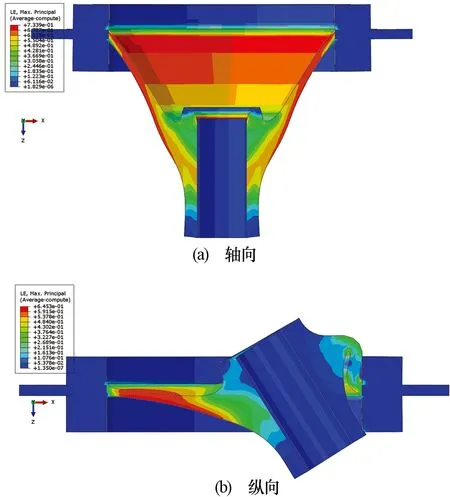
图4 橡胶隔振器静态应变分布截面图
橡胶隔振器的蠕变和应力松弛曲线如图5所示,0~0.01 s为静态力或位移加载过程,0.01~1 s为保持载荷或边界条件不变时的渐变过程。橡胶隔振器在蠕变过程中位移缓慢增加并趋于稳定,1 s时由于蠕变产生的偏离位移约为静态位移的13.4%。橡胶隔振器在应力松弛过程中隔振器受力先急剧减小,而后缓慢变小并趋于稳定,1 s时由于应力松弛产生的偏离载荷约为静态载荷的36.7%。这些准静态特性与典型的橡胶蠕变和应力松弛行为在变化趋势上是一致的。
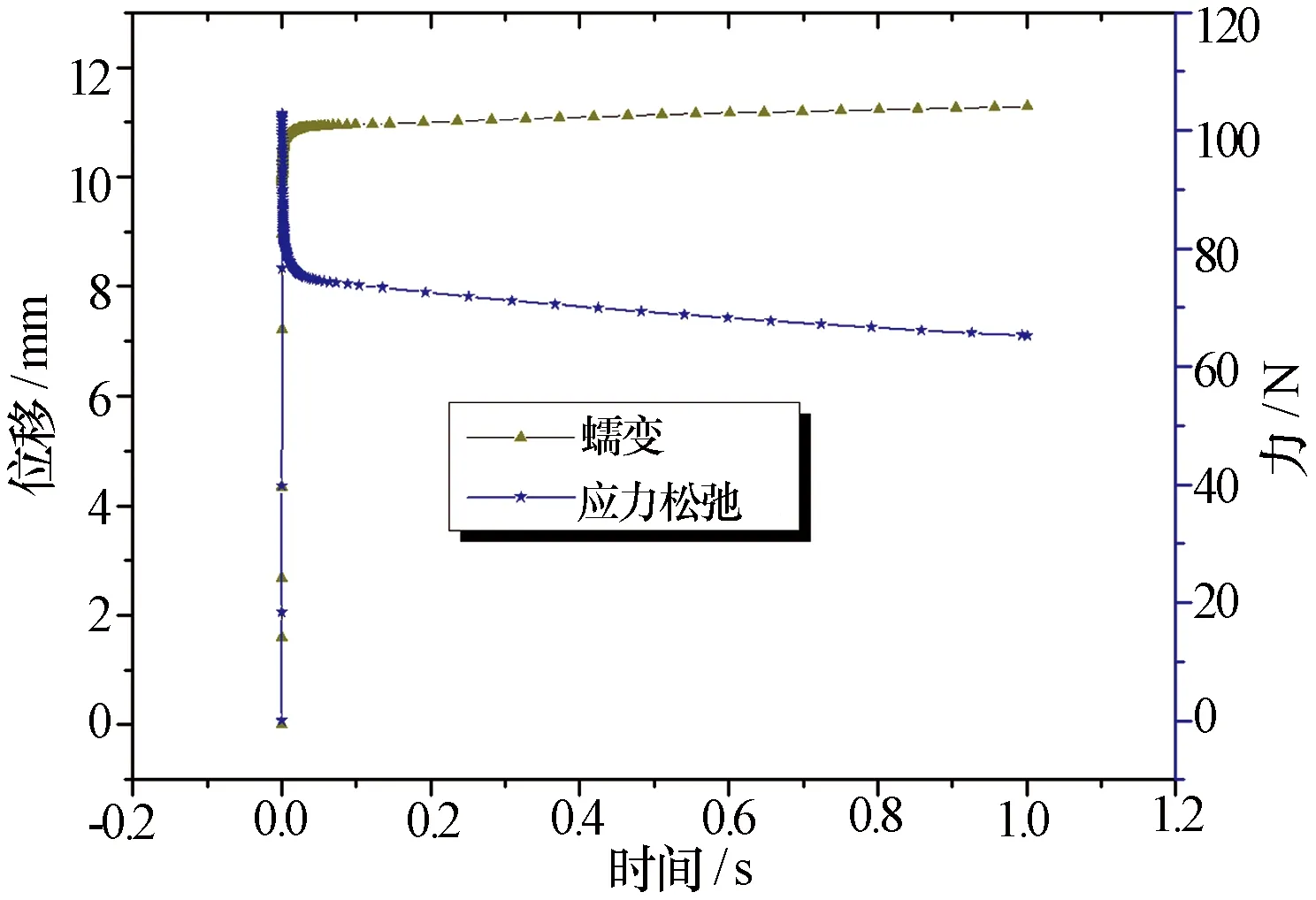
图5 橡胶隔振器静蠕变和应力松弛曲线
4 橡胶隔振器动态特性
图6为模拟得到的激励频率为20 Hz时的橡胶隔振器轴向动态特性曲线,分别为仅考虑橡胶超弹性和考虑橡胶粘超弹性下隔振器支反力与加载位移的关系曲线。从图6可以看出:仅考虑橡胶超弹性时,加载曲线与卸载曲线重合,系统无能量耗散;考虑橡胶粘超弹性时,加载曲线与卸载曲线不重合,形成一个封闭的迟滞回环,该回环的面积即为由材料粘性损耗引起的能量耗散。
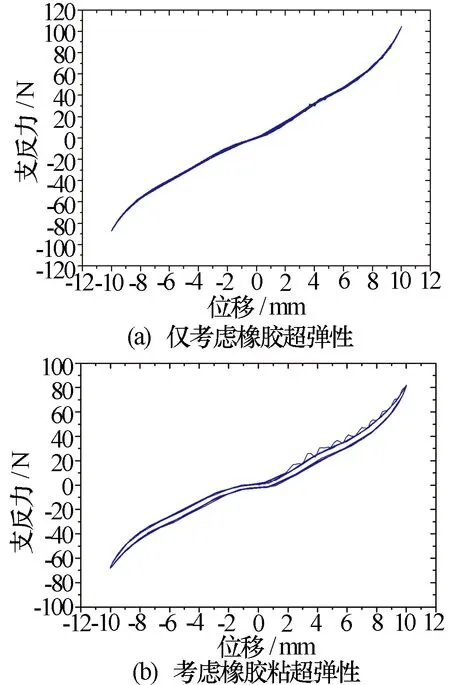
图6 橡胶隔振器轴向动态特性曲线
橡胶隔振器动刚度Kd和阻尼角δ可以由以下公式计算得到:
Kd=F0/X0
(2)
(3)
式中:F0为力的幅值;X0为位移的幅值;Uc为迟滞回环的面积。
橡胶隔振器动态特性与激励频率息息相关,为此考察了0.1~60 Hz范围内橡胶隔振器动刚度和阻尼角随激励频率的变化曲线,如图7所示。从分析结果可以看出:动刚度随着激励频率的增加而增加,橡胶隔振器具有刚度强化效应,且在低频段(0.1~1 Hz)时变化较为显著,高频段时变化较为平缓;阻尼角随着激励频率的增加先急剧减小,而后缓慢增加,因此橡胶隔振器在某一低频点处能量耗散最低。
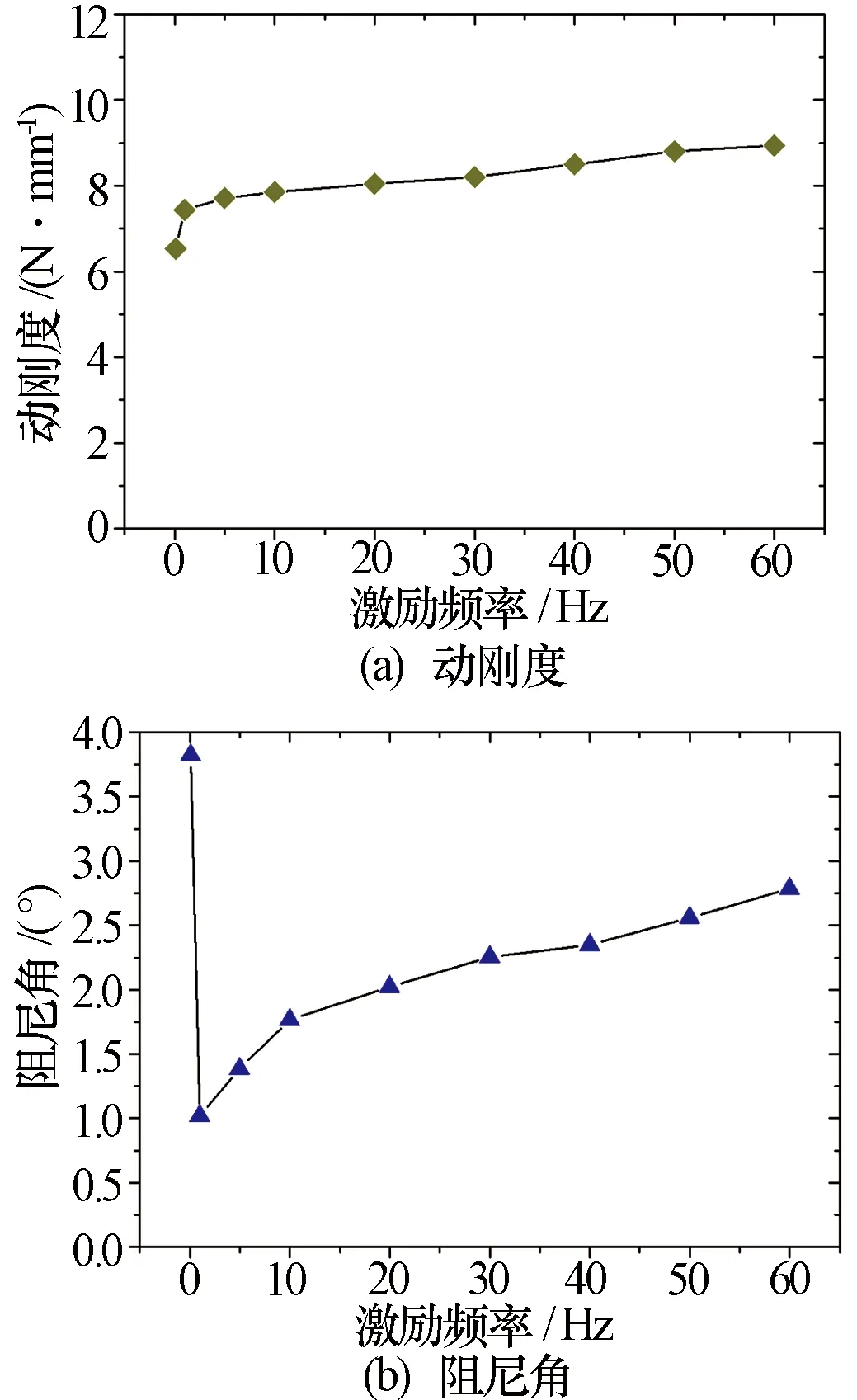
图7 橡胶隔振器动态特性随激励频率变化曲线
图8为模拟得到的频率范围在0 ~1 000 Hz内的橡胶隔振器谐响应特性曲线。从分析结果可以看出,隔振器位移输出曲线除了在几个共振频率点处的位移响应较大之外,其余频率段的位移响应均处于较低水平。由于基础位移幅值为1 mm,因此隔振器的传递率曲线(隔振器位移输出与基础位移输入之比)与隔振器位移输出曲线重合,传递率在共振频率为17 Hz时约为6.4,在共振频率为307 Hz和662 Hz时约为0.6,其余均低于0.1。
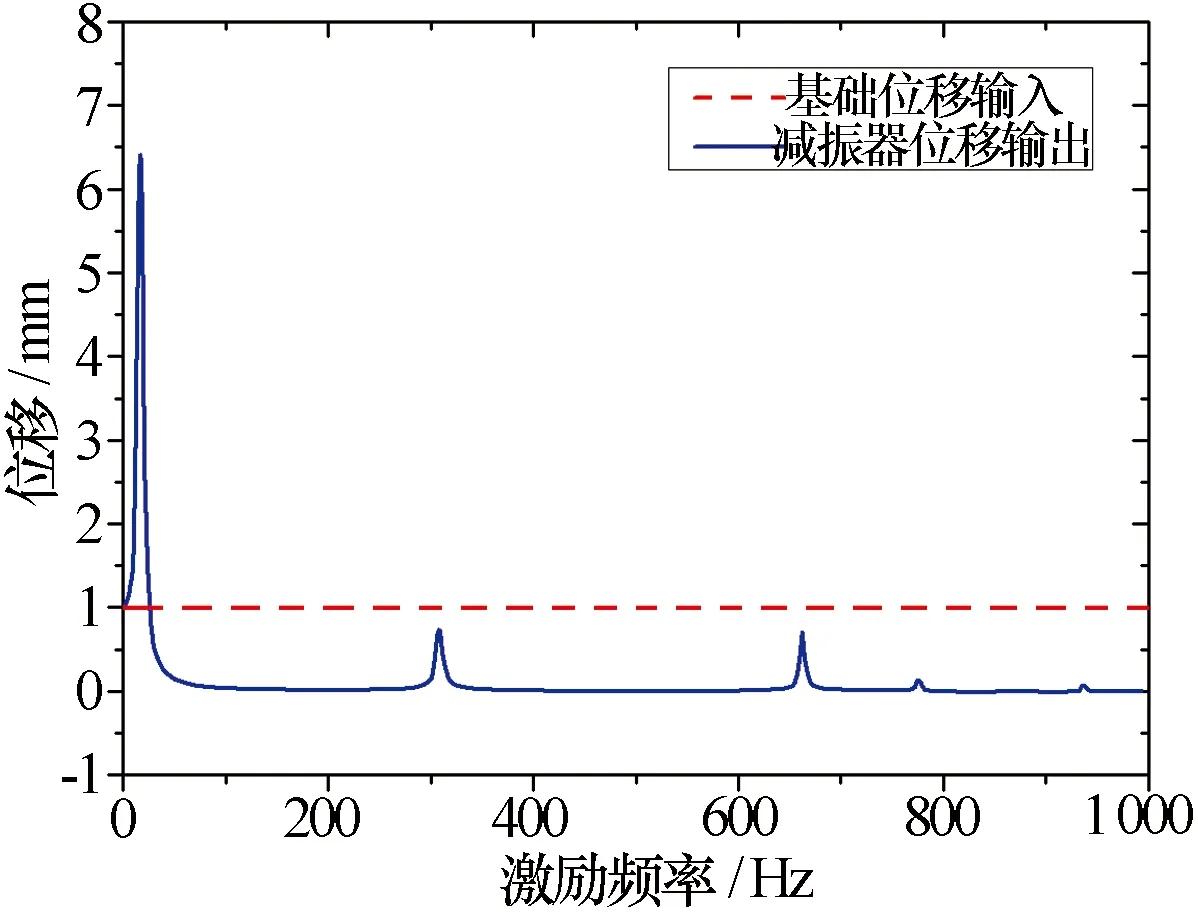
图8 橡胶隔振器动态特性谐响应曲线
图9为橡胶隔振器在峰值为20g的后峰锯齿波冲击条件下的加速度自由衰减响应曲线。冲击持续时间为11 ms,隔振器加速度输出在18 ms时达到第1个最大峰值,约为15.56g,据此计算冲击传递率Tsa:
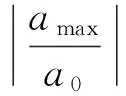
(4)
式中:amax为第1个最大峰值;a0为输入时的加速度峰值。
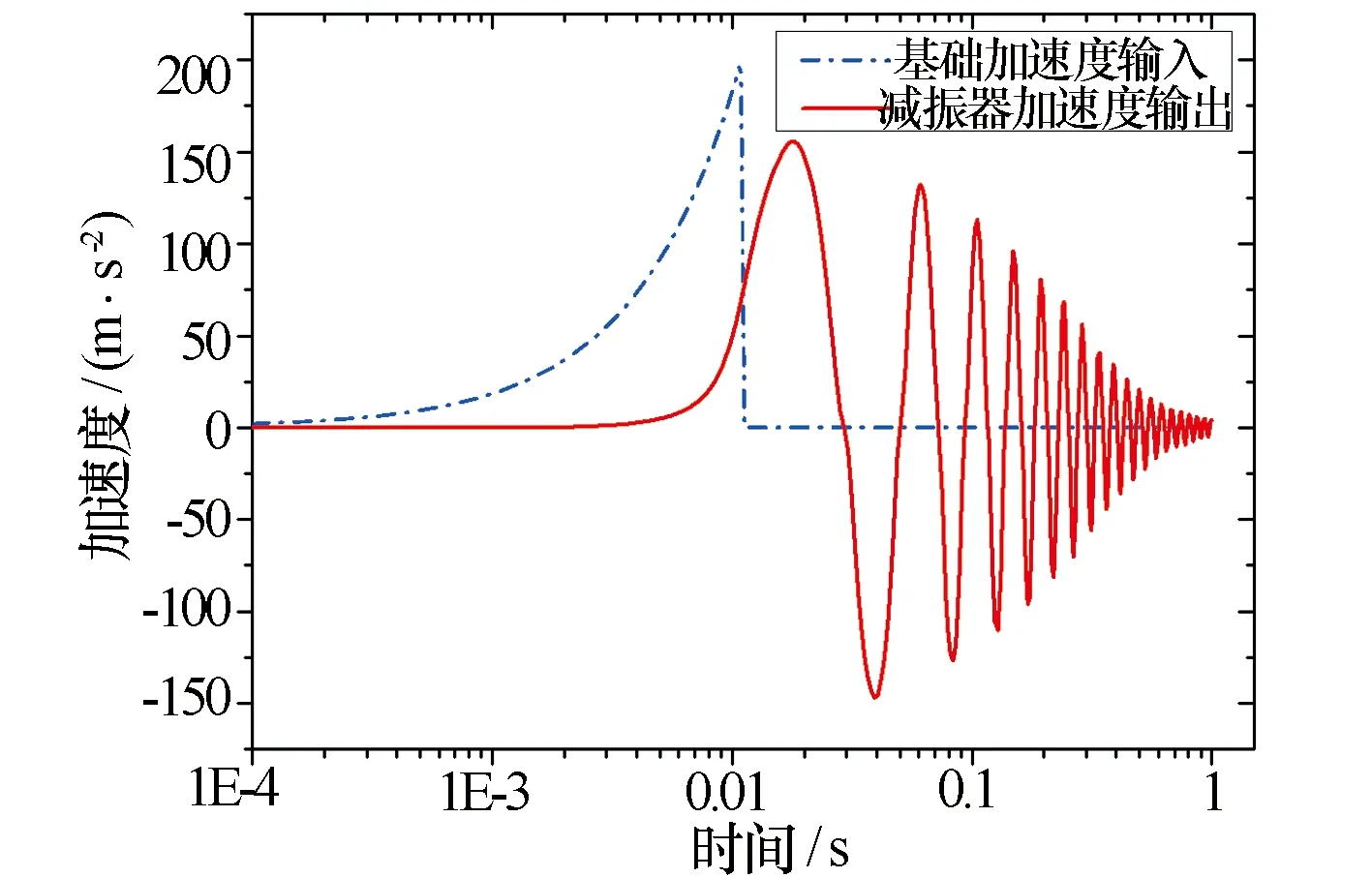
图9 橡胶隔振器在冲击条件下加速度自由衰减响应曲线
5 关键参数设计
基于以上分析方法,重点考察了橡胶隔振器设计和选型中的2个关键参数,橡胶超弹性和匹配质量(隔振器件质量)对减振性能的影响。
由于橡胶材料配方较多,材料性能参数差别较大,其最主要的超弹性性能更是千差万别。图10为采用5种超弹性材料参数(M0~M4,M0为上文分析采用的超弹性材料参数)时的橡胶隔振器谐响应曲线对比结果。从图10可以看出橡胶超弹性材料特性对隔振器谐响应特性的影响较大,各自的共振频率及传递率均不相同。因此在进行隔振器设计时除了构型设计之外,还必须关注材料的超弹性特性,以合理设计其动态减振行为。
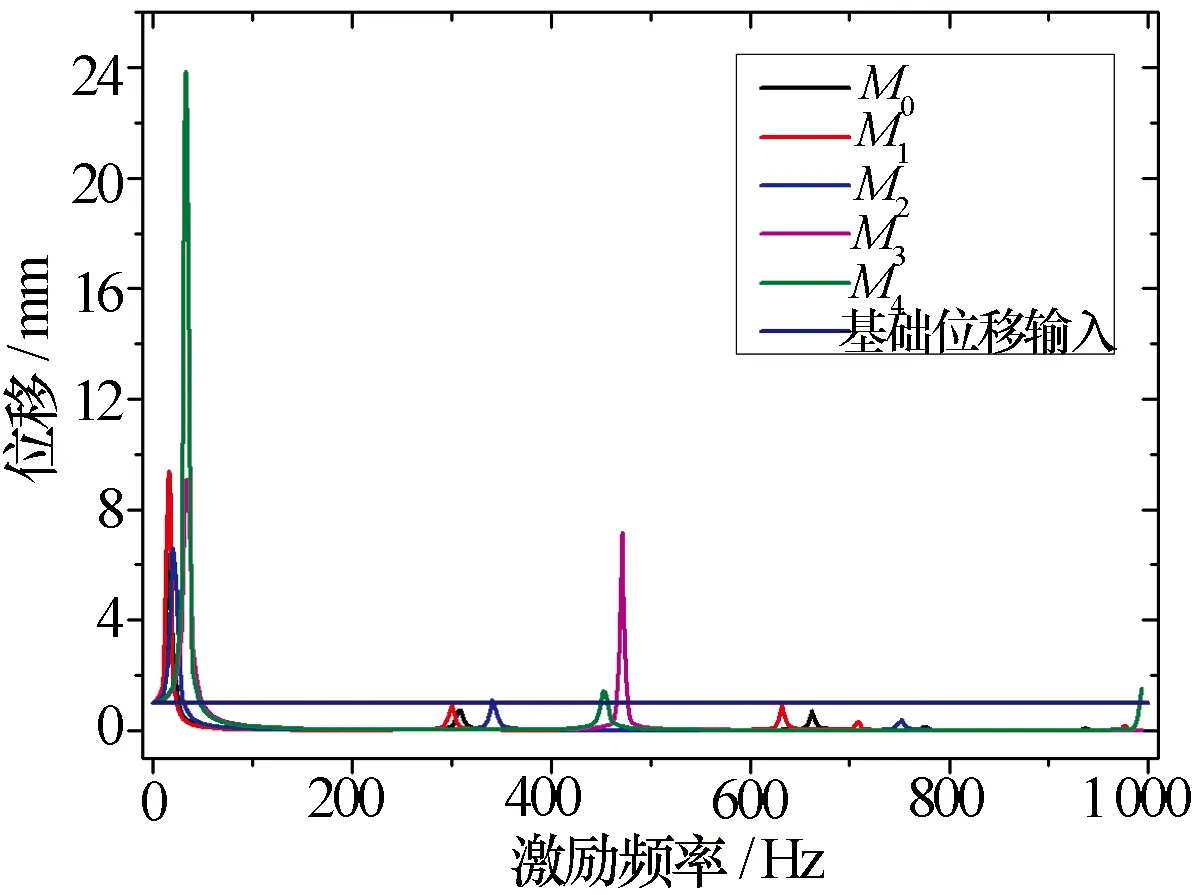
图10 橡胶超弹性特性对谐响应特性的影响
橡胶隔振器一般具有特定的使用范围,对于橡胶隔振器选型来说,匹配质量是最基本的参数。图11为采用不同匹配质量下隔振器的第1个最大峰值加速度滞后时间和加速度峰值的变化曲线。从图11可以看出:在所考查的匹配质量范围内,滞后时间随着匹配质量的增加而增加;加速度峰值随着匹配质量的增加先减小后增加,在0.5 kg附近时达到极小值,且在0.125 kg时加速度峰值大于冲击输入峰值(20g),此时橡胶隔振器未起到减振的作用,相反隔振器件的加速度输入反而放大。由此可见,隔振器选型时必须对匹配质量进行严格分析,方能起到预想的减振效果。
6 结束语
针对电子设备中橡胶隔振器的静动态特性分析方法问题,系统建立了一套基于非线性有限元方法的求解策略,以某型橡胶隔振器为例获得了其静刚度、蠕变和松弛特性等静态特性以及迟滞回环、谐响应和冲击响应等动态特性,并对橡胶隔振器设计和选型中的2个关键参数(橡胶超弹性和匹配质量)进行了讨论,可为橡胶隔振器设计方法研究提供参考。
[1] 平丽浩, 黄普庆, 张润逵, 等. 雷达结构与工艺[M]. 北京: 电子工业出版社, 2007.
[2] SHAW M T, MACKNINGHT W J. 聚合物黏弹性引论[M]. 上海: 华东理工大学出版社, 2012.
[3] 王锐. 橡胶隔振器动力学性能及设计方法研究[D]. 武汉: 华中科技大学, 2007.
[4] 潘孝勇. 橡胶隔振器动态特性计算与建模方法的研究[D]. 杭州: 浙江工业大学, 2009.
[5] 钱胜. 汽车橡胶隔振元件动静态特性研究及优化设计[D]. 合肥: 合肥工业大学, 2012.
[6] 张丽霞. 快速货车橡胶减振元件静动态特性分析[D].成都: 西南交通大学, 2013.
[7] 黄友剑, 张亚新, 卜继玲, 等. 基于显式积分技术求解大变形橡胶减振元件非线性准静态刚度的方法[J]. 中国铁道科学, 2012, 33(3): 74-78.
[8] 周相荣, 王强, 王宝珍. 一种基于Yeoh函数的非线性粘超弹本构模型及其在冲击仿真中的应用[J]. 振动与冲击, 2007, 26(5): 33-37.
[9] 黄德东, 吴斌, 徐超. 橡胶隔振器动刚度有限元数值预测方法研究[J]. 机械科学与技术, 2013, 32(5): 660-664.
[10] 克拉夫 R, 彭津 J. 结构动力学[M]. 王光远, 译. 北京: 高等教育出版社, 2006.
李 钊(1985-),男,高级工程师,博士,主要从事军用雷达装备力学仿真、测试与优化设计工作。
声 明
为适应我国信息化建设,扩大本刊以及作者的知识信息交流渠道,本刊已被封面上的数据库全文收录,其作者文章著作权使用费与本刊稿酬一次性付给。如作者不同意文章被收录,请在来稿时向本刊申明,本刊将作适当处理。
Study on Static and Dynamic Characteristics of Rubber Isolator forElectronic Equipment
LI Zhao,PENG Chao,WANG Zhi-hai
(National Industrial Design Center, the 38th Research Institute of CETC, Hefei 230088, China)
The viscoelastic damping material is used to provide vibration/shock protection and control of the rubber isolator. Traditionally, trial and error design are carried out by a large number of empirical formulas and test data, which is characterized by low efficiency and high cost. Aiming at the static and dynamic characteristics analysis problem of the rubber isolators in electronic equipment, a nonlinear finite element method is proposed to solve the problem. By taking a rubber isolator as an example, the static characteristics such as static stiffness, creep and relaxation properties and the dynamic characteristics such as hysteresis loop, harmonic response and impact response are obtained. And the two key parameters (rubber hyperelasticity and matching mass) in the design and selection of the rubber isolator are discussed, which can provide reference for the design method study of the rubber isolator.
rubber isolator; static stiffness; dynamic stiffness; vibration; impact
2016-11-27
TU112.59
A
1008-5300(2017)03-0020-05
