一道赛题的再思考

广东省广州市协和中学 (510160)

许云勇

一道赛题的再思考

广东省广州市协和中学 (510160)

许云勇

上述不等式也曾经作为第三届国际中学生数学竞赛试题，应该说它是数学中的一道经典不等式，对于该不等式，代数证明方法有多种，但基本上都是难以入手、计算量大，对学生的分析能力、计算能力都要求较高，笔者最近对该不等式作了一些探讨，得到一种更为简洁的几何证法，同时得到与上述不等式相关的两个新不等式链，现与读者分享.

一、结论的几何证明

证明：在ΔABC中不妨设a≥b≥c,如图1，以BC为边构造等边ΔA′BC，记AA′=d,则∠ABA′=B

图1

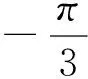
注：抓住不等式中等号成立的“关键”时刻，巧妙地通过分析一般时刻与关键时刻的异同，从而使得待证不等式通过几何关系、代数运算得以体现！

二、相关的不等式链

事实上，对于不等式(1)，我们可以得到一个更为完美的一个如下不等式链：

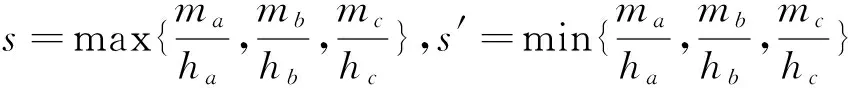
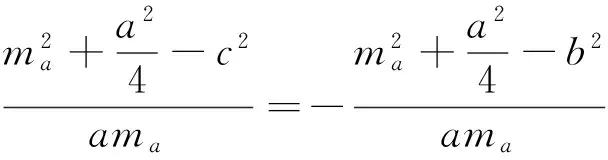
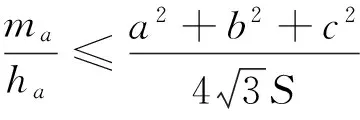
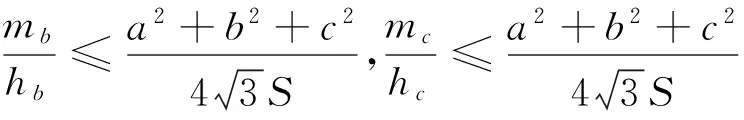
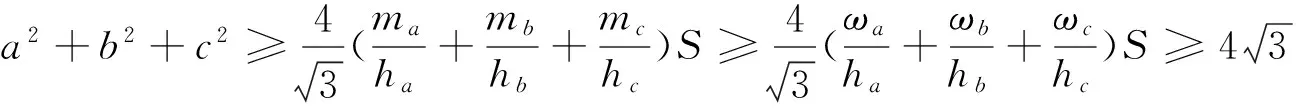
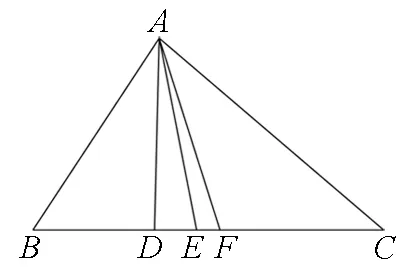
图2

若AC=AB,不难看出ha=ωa=ma.故ha≤ωa≤ma,同理可得hb≤ωb≤mb,hc≤ωc≤mc.

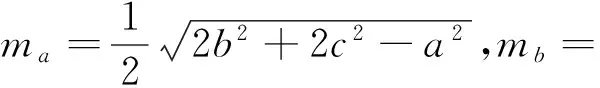
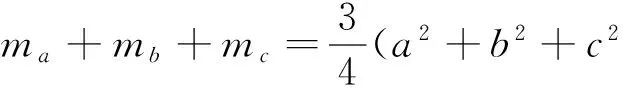
而由柯西不等式可知(a2+b2+c2)(ma+mb+mc)≥(ama+bmb+cmc)2,