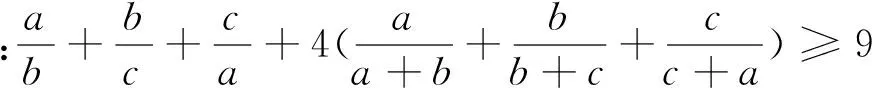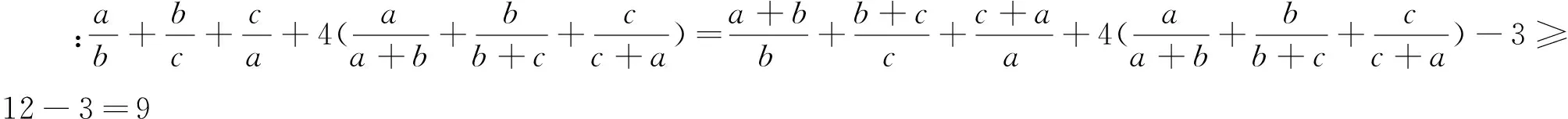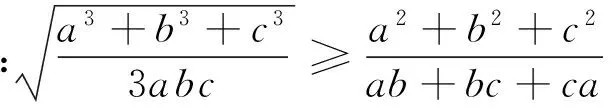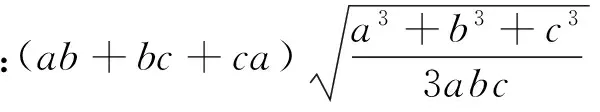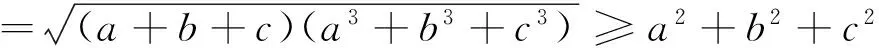2017年数学竞赛不等式赏析
2017-08-28浙江省绍兴鲁迅中学312000
中学数学研究(江西) 2017年8期
浙江省绍兴鲁迅中学 (312000)
陈少春
2017年数学竞赛不等式赏析
浙江省绍兴鲁迅中学 (312000)
陈少春
笔者把近期部分世界各地的不等式问题做了一些整理,与各位专家和读者一起欣赏.
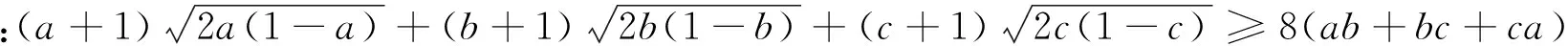

引申 该不等式还有上界:
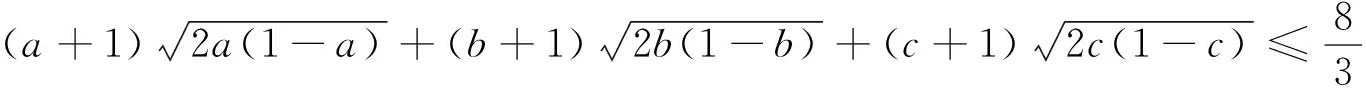
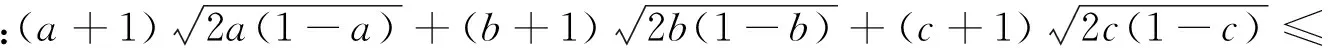
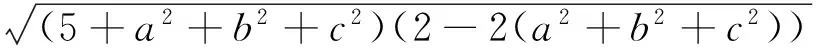
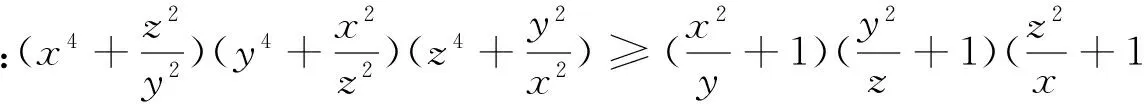
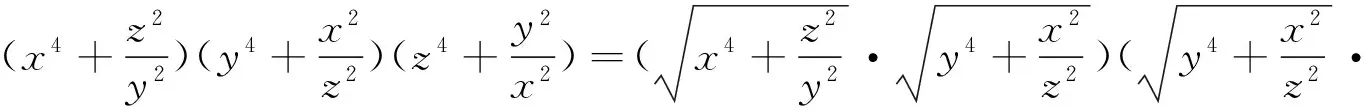
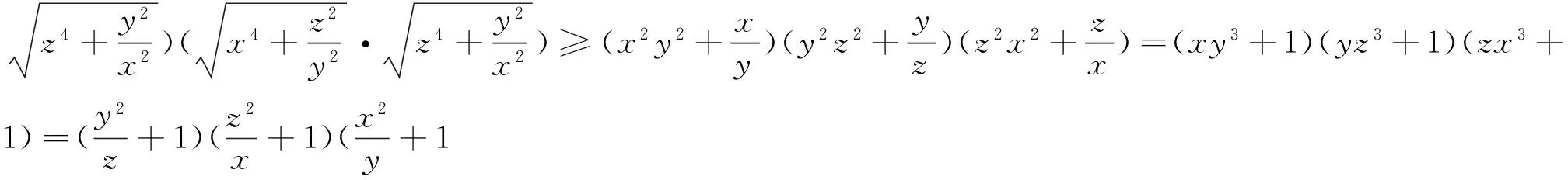

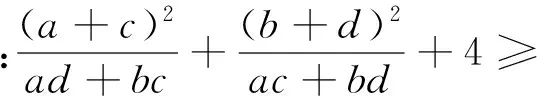
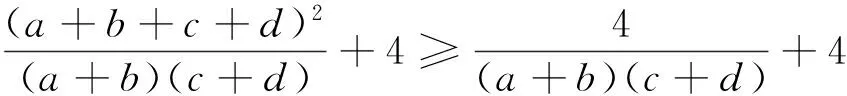
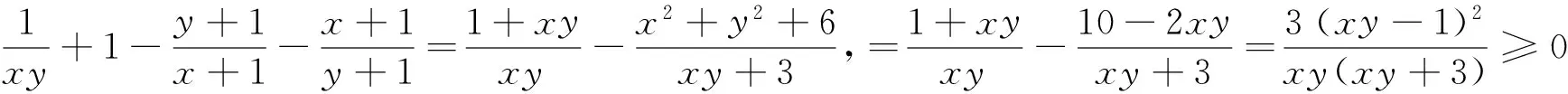



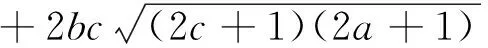
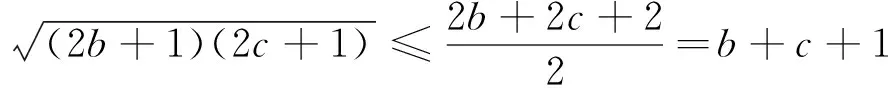
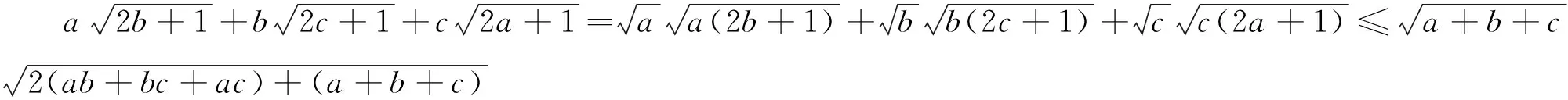
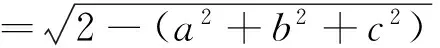
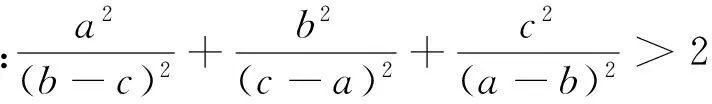

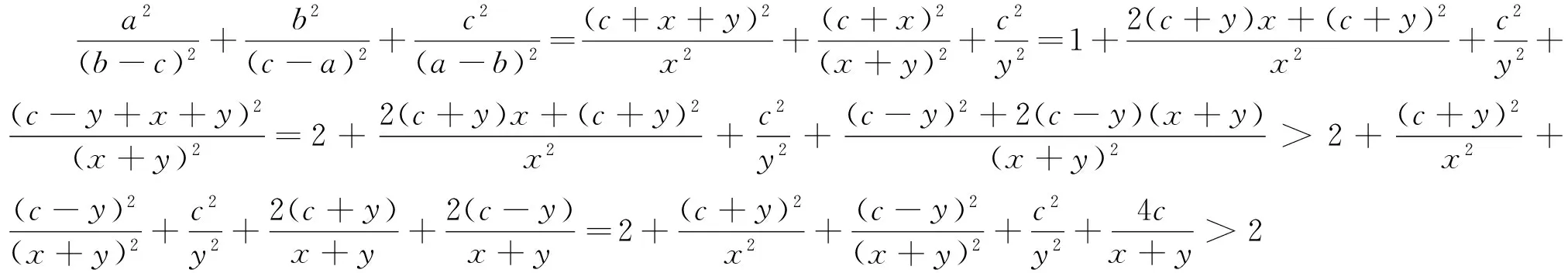

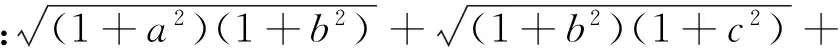
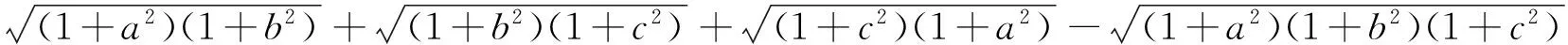
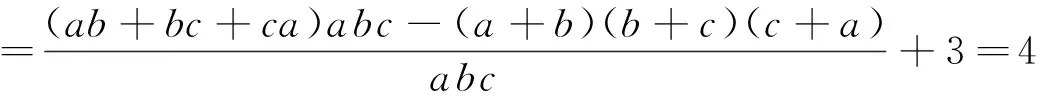
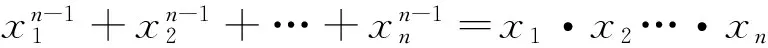
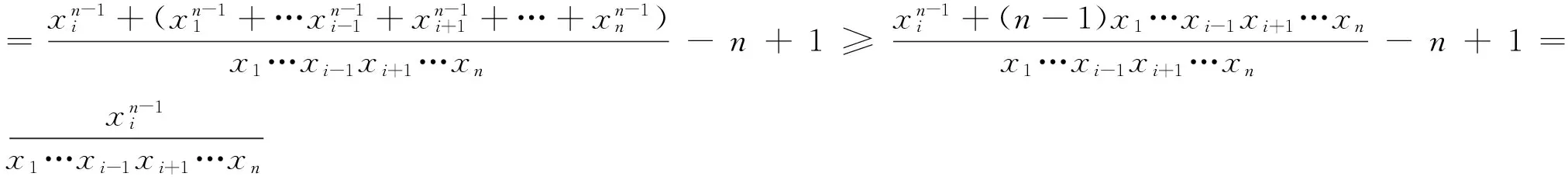
证明:(1+absin (β-α))2=1+2absin (β-α)+a2b2sin2(β-α)=1+2absin (β-α)+a2b2(1-cos2(β-α))≥1+2absin (β-α)+a2b2-(1-a2)(1-b2)=2absin (β-α)+a2+b2=(acosα+bsinβ)2+(asinα-bcosβ)2≥(acosα+b·sinβ)2,又acosα+bsinβ>0,1+absin (β-α)>0,所以acosα+bsinβ≤1+absin (β-α).