水下发射航行体出水过程瞬态响应的谱分析方法
2017-08-28吕海波岳之光武龙龙赵振军
吕海波,岳之光,武龙龙,李 明,赵振军
(北京宇航系统工程研究所,北京 100076)
水下发射航行体出水过程瞬态响应的谱分析方法
吕海波,岳之光,武龙龙,李 明,赵振军
(北京宇航系统工程研究所,北京 100076)
水下航行体在穿越水面时,受到移动式空泡溃灭压力作用,激起结构较大瞬态响应,因此其出水问题是工程设计的关注焦点。针对移动载荷作用下的水下航行体的瞬态响应问题,提出了基于冲击响应谱的谱分析方法,对于多模态下的综合方法进行了研究和比较,并对航行体出水动态响应进行了分析。采用本文方法可以在频域中迅速地获得结构动态响应解,并与时域解具有较好的一致性,且可以考虑外力随机分布下的动态响应,具有较好的适应性。
移动载荷;瞬态响应;空泡溃灭;冲击谱
0 引言
水下航行体在水下高速运动时,表面有空泡产生。而在穿越水面时,空泡发生溃灭[1-2],形成较大溃灭压力,从而激起结构较大瞬态响应,严重时可能造成结构破坏,因此高速航行体的出水问题是工程设计的关注焦点。目前仿真和实验结果表明,空泡溃灭压力在航行体表面是逐步推进的[3],呈现出移动载荷的特点。
对于航行体出水瞬态响应计算问题,目前已开展了相关研究[4-5],提出了瞬态响应计算方法。针对移动载荷,在桥梁、铁路领域也开展了一些研究[6-8]。在这些研究中,为获得精确解,主要采用时域求解的方法。但由于航行体结构复杂,影响因素众多,时域求解效率较低,多工况下难以快速获得所需结果。另一方面,由于外力具有较大随机性,因此结构响应的时域解也具有较大随机性,且由于不同模态振动之间相位差异,为工程设计应用带来了困难。
采用频域方法则可以快速对结构瞬态响应问题进行求解。考虑到这一优点,本文基于冲击响应谱的方法提出了一种移动载荷作用下方法航行体瞬态响应求解方法,并对载荷移动速度等参数对响应的影响规律进行了研究。
1 梁在移动载荷下的响应计算
首先考虑图1所示简支梁在移动载荷作用下的瞬态响应问题,即外力F以速度v从梁一端扫向另一端。梁的横向振动微分方程为:
(1)
式中,E为材料弹性模量,I为梁截面惯性矩,A为截面面积,ρ为材料密度,y为挠度。
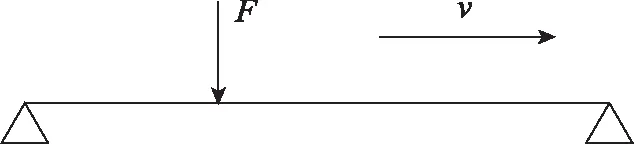
图1 受移动载荷作用下的简支梁Fig.1 Simply supported beam under a moving load
对于均匀梁的自由振动,式(1)变为:
(2)
而对于均匀简支梁,第i阶固有圆频率ωni为:
(3)
式中,l为梁的长度。其质量归一化振型φi可以用正弦函数来描述:
(4)
对于移动载荷,考虑集中力情况,当其移动速度为v时,对于第i阶振型而言,其运动方程为:
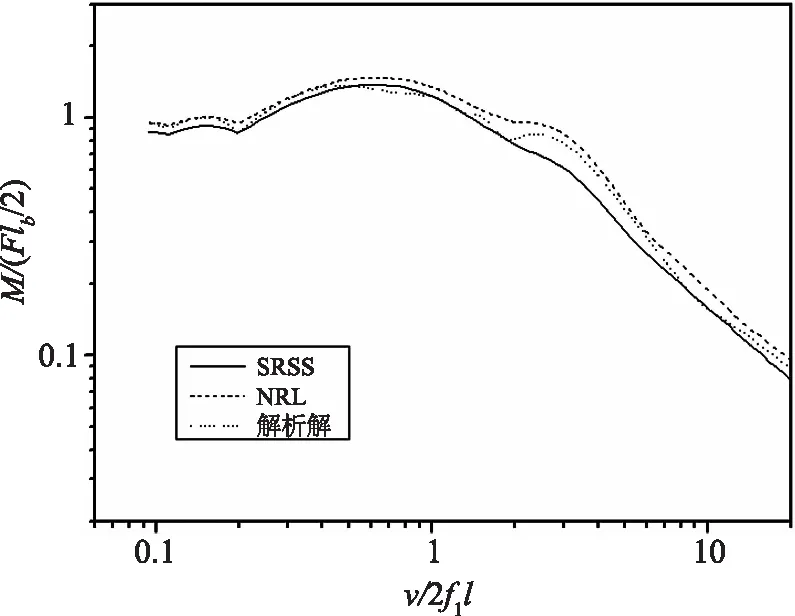
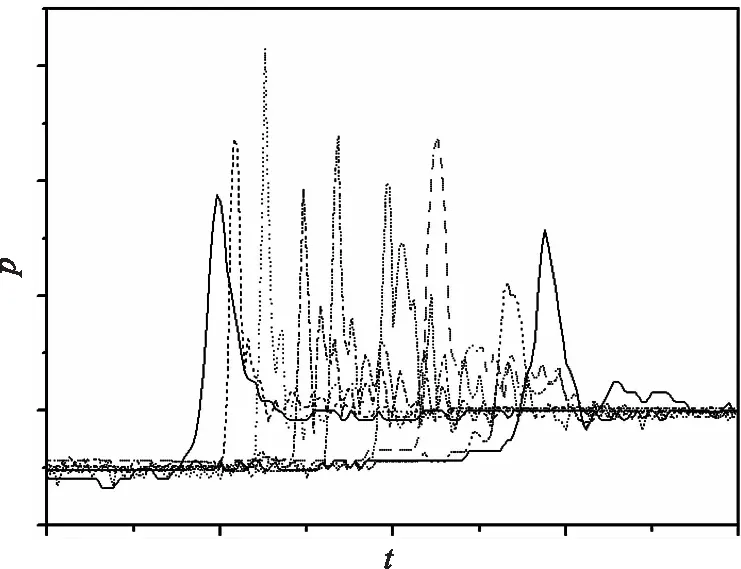
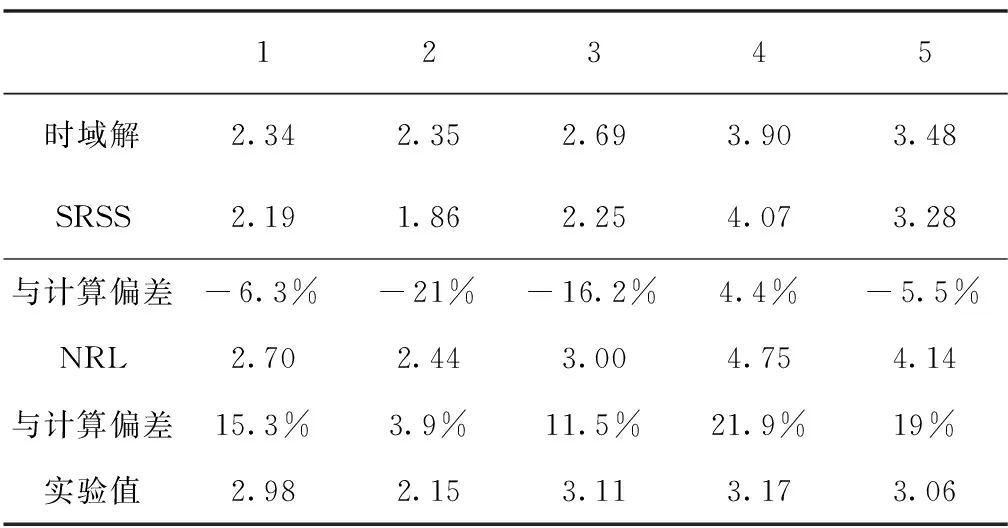
t 其中,qi为第i阶广义坐标,ζi为第i阶模态阻尼比。移动载荷在模态空间内就可以简化为若干个半正弦载荷组成的瞬态外力造成的冲击问题。 对于均匀简支梁某模态的运动方程,可以通过时域求解或解析解获得。实际上,工程中关注最大解的情况,对此采用冲击响应谱则可以迅速求解。冲击谱是指一有阻尼(或无阻尼)的单自由度振子受到一定冲击载荷作用下,振子的相对位移(或速度、加速度)的最大幅值随频率的变化关系。当冲击载荷为输入力时,系统的响应由Duhamel积分求得: (6) 在求得广义坐标最大解qi,max后,乘以振型可以得到该阶模态最大位移,或乘以模态弯矩、模态剪力等得到梁截面的弯矩、剪力。 对于自由-自由边界的梁模型,在计算中可基于公式(5)求得广义力Fφi(vt),并进一步求解得到该阶模态的响应。 在获得了各阶模态的最大响应后,可以将其进行叠加。由于从冲击谱求得的最大响应值忽略了相位和符号,因此无法获得如时域求解得到的精确解。但可以采用适当方法组合各阶最大响应,获得具有统计意义的合成解[9]。一般包括以下方法: (1)绝对值求和(ABS) (7) (2)2阶矩叠加(SRSS) (8) (3)美国海军研究实验室求和(NRL)[10] (9) 其中,yj,max是各模态中最大的模态响应。此方法将最大模态响应加到其余之和的平方根上。 (4)10%叠加法 (10) 该方法是对SRSS方法的改进,是为了考虑频率接近的模态间的叠加影响。一般规定频率值相差在10%以内的模态需考虑其相互作用,即 (11) 3.1 简支梁的响应 为验证本文方法,考虑一根5m长的简支梁,横截面边长为100mm,厚度为5mm的正方形,材料为钢,阻尼比为0.025。考虑前3阶弯曲模态,采用本文的方法对移动载荷F在不同速度下的响应,并与解析解进行对比分析。在此对梁1/4、1/2长度位置截面处的弯矩结果进行了计算,并对其进行了无量纲化处理,结果如图2所示。 (a)1/4长度处 (b)1/2长度处图2 移动载荷作用下的简支梁不同截面的弯矩Fig.2 Section moments of simply supported beam under moving loads 从计算结果可以看出,SRSS与NRL的趋势一致,且NRL解略高于SRSS。整体而言,NRL值基本高于时域解析解,是偏保守的;而SRSS值则可能漏掉危险工况。梁中点的弯矩最大,其时域解与NRL值吻合较好,误差较小,且弯矩最大值出现在v/2l约2/3的1阶频率处,表明在该速度下梁会被激起最大响应;而随着速度的增加,梁的响应逐渐减小。而1/4长度处的时域解与谱分析结果存在一定差别,误差较大,这主要是不同阶模态振动相位不同导致的。1/4长度处的时域解最大值出现在v/2f1l=2.1处,而谱分析结果表明在0.6~1.5的较宽范围内,该处均会出现较大响应。可以看出,应用谱方法与时域解联合开展研究,更有助于开展全面分析。 3.2 水下航行体出水响应 针对某水下航行体在出水过程中的响应采用本文方法进行了分析。该航行体在出水过程中受到的空泡溃灭压力如图3所示,可以看出,随着时间的推移,溃灭压力不断向后移动,且溃灭压力的量值和宽度也具有一定分散性,并随时间发生变化。在该移动载荷作用下,航行体结构中将产生较大动响应。 图3 移动式的空泡溃灭压力Fig.3 Moving cavity collapse pressure 在计算中考虑了航行体前5阶横向模态,其频率如表1所示,前两阶振型如图4所示。计算结果见表2,表中M1为1阶模态弯矩。可以看出,采用谱分析法可以获得与时域解较为一致的结果,其偏差在25%以内。同样的,NRL解大于SRSS解和时域解,是偏保守的。结果表明谱分析法具有较好的适应性,且能较好地考虑水动力的分散性。 表1 航行体各阶频率 表2 航行体截面弯矩计算结果(M/M1)对比 图4 航行体前两阶横向振型Fig.4 The first two transversal mode shapes 本文针对移动载荷作用下的水下航行体的瞬态响应问题,提出了基于冲击响应谱的谱分析方法,对于多模态下的综合方法进行了研究和比较,并对航行体出水动态响应进行了分析。结果表明: 1)采用本文方法可以在频域中迅速获得动态响应解,并与时域解具有较好的一致性。 2)外载荷的移动速度对结构响应有显著影响,且不同位置处的最大响应对应的临界速度与模态相关。 3)NRL解整体而言偏保守,本文方法可以考虑外力随机分布下的动态响应,具有较好的适应性,可用于工程设计。 [1] 尤天庆,张耐民,魏海鹏,等. 含气空泡出水过程数值模拟研究[J]. 振动与冲击,2015,34(18):106-110. [2] 王一伟,黄晨光,杜特专,等. 航行体垂直出水载荷与空泡溃灭机理分析[J]. 力学学报,2012,44(1):39-48. [3] 赵蛟龙,孙龙泉,张忠宇,等. 航行体出水空泡溃灭载荷特性研究[J]. 哈尔滨工业大学学报,2014,46(7):81-86. [4] 吕海波,权晓波,尹云玉,等. 考虑水弹性影响的水下航行体结构动响应研究[J]. 力学学报,2010,42(3):350-356. [5] 李国良,袁湘江,敖林. 潜射导弹出水载荷数值算法研究[J]. 力学与实践,2013,35(4):25-30. [6] 周华飞,蒋建群. 高速移动荷载下黏弹性半空间体的动力响应[J]. 力学学报,2007,39(4):545-553. [7] 付世晓,崔维成,陈徐均,等. 移动载荷作用下非线性连接浮桥的动力响应[J]. 上海交通大学学报,2006,40(6):1004-1009. [8] Michaltsos G, Sophianopoulos D, Kounadis A N. The effect of a moving mass and other parameters on the dynamic response of a simply supported beam[J]. Journal of Sound and Vibration, 1996, 191(3) : 357-362. [9] 贺少华,吴新跃. 转子系统冲击响应谱分析法研究[J]. 兵工学报,2010,31增刊(1):22-27. [10] O′Hara G J, Belsheim R O. Interim design values for shock design of shipboard equipment[R]. Washington DC: U. S. Naval Research Laboratory, 1963. A Spectrum Analysis Method of Dynamic Response of Underwater Vehicles under Moving Loads LYU Hai-bo, YUE Zhi-guang, WU Long-long, LI Ming, ZHAO Zhen-jun (Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China) The moving cavitation collapse pressure is the major excitation of structural transient response of underwater vehicles in the water-exiting process, which is an important focus in engeering design. A spectrum anslysis method based on shock response spectrum is applied to solve the dynamic response problem of underwater vehicles under moving loads. Different mode combination methods are analyzed and compared with experiments. The structure dynamic response results is able to obtained rapidly in frequency domain with this spectrum analysis method. The results also show good agreement with the time domain solution. Besides, the random distribution of loads is concerned in the method, which meets the reality well. Moving loads; Dynamic response;Cavitation collapse; Shock response spectrum 2017-01-09; 2017-03-17 总装备部预研基金(9140A14060311HT1901) 吕海波(1974-),男,硕士,研究员,主要从事结构动力学方面的研究。E-mail:lutro@tom.com O352/V215.5 A 2096-4080(2017)02-0042-04
2 多模态解合成
3 计算与分析



4 结论
