基于凯恩动力学的AUV建模

孙佳杰，杨柯，葛彤

（1.杭州电子科技大学机械工程学院，杭州310018；2.上海交通大学船舶海洋与建筑工程学院，上海200240）

基于凯恩动力学的AUV建模

孙佳杰1，杨柯1，葛彤2

（1.杭州电子科技大学机械工程学院，杭州310018；2.上海交通大学船舶海洋与建筑工程学院，上海200240）

推导出基于凯恩动力学的AUV运动学和动力学方程。采用广义速度取代速度和角速度，给出了广义惯性力和广义主动力的计算方法。推导出作用在AUV上的水动力的计算方法，并通过仿真实验给出了水动力系数。为了验证该模型的有效性，对AUV的深度控制、前进距离控制进行了仿真。仿真结果表明，该模型是有效的。

凯恩动力学；AUV；建模；广义速度

0 引言

计算机建模和仿真可以为机器人的研究提供巨大的帮助。动力学模型可以通过调整设计参数和水动力系数优化机器人的性能。AUV的动力学模型是研究AUV运动控制以及机械设计的基础。机器人的动力学可以采用理论力学和分析力学的动力学方程（例如，Newton-Euler（N-E）动力学方程、Lagrange-Euler（L-E）方程、Routh方程、Appell方程、Kane方程）来分析。采用不同的建模方法对同一机器人进行建模，最终结果是相同的。但是，运算速度和质量有很大差别。而运算速度和质量恰恰是实时控制的关键[1-2]。

N-E方程包含机器人模块间的相互作用力，很难消除该作用力以便获得机器人运动与受力之间的清晰表达式[3]。因此，N-E方程主要用于机器人设计阶段的受力分析。L-E方程、Routh方程和Appell方程通常为非线性差分方程，求解该方程时耗时长、运算速度慢[4-6]。Kane方程是1970年发展起来的分析力学的分支，方程的形式非常简单（只需加、减、乘、除运算），因此，非常适合创建复杂系统的动力学方程用于实时控制。例如，夏丹[7]提出了基于Kane动力学的机器鱼的波状运动模型；李新友[8]创建了基于Kane动力学的3UPS/S关联机构动力学模型；沈飞[9]提出基于Kane动力学的机器海豚动力学模型；Cheng[10]分析了四自由度平行髋关节模拟器的运动学；Liu[11]提出采用Kane动力学方程创建多体系统的动力学方程。Yang[12-13]推导出基于Kane动力学方程的水下蛇形机器人和水下四足行走机器人的动力学模型。

尽管Kane动力学已经出现在一些机器人的建模中，基于Kane动力学的AUV动力学模型仍然没有出现。本文提出了基于Kane动力学的AUV建模方法，该方法消除了N-E方程中的相互作用力和L-E方程中的势能或Gibbs方程。Kane方程采用广义速度，可以为非正交约束系统选取一组相互独立的运动变量，以便获得一阶差分方程形式的动力学模型。Kane方法可以将外部环境的作用力直接添加到AUV动力学方程，该方程可以方便地转化为适用于控制的闭环形式。AUV动力学方程可以为“哪些力真正影响动力学模型”提供物理解释。

1 水动力

1.1 水动力计算公式

AUV在运动过程中受到的水动力主要包括：浮力、附加质量力、附加质量矩、柯氏力、柯氏力矩、拖曳力和拖曳力矩。浮力可表示为

式中：ρ表示流体的密度；V表示AUV排开水的体积；g表示重力加速度。

附加质量力和附加质量矩取决于AUV的形状。考虑到AUV的对称性和载体坐标系原点的位置，附加质量力和附加质量矩可以表示为：

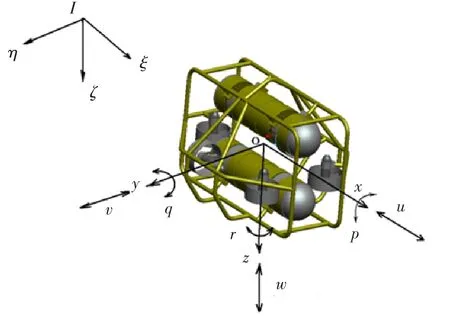
图1 AUV惯性坐标系与载体坐标系Fig.1 The inertia frame and body frame of AUV

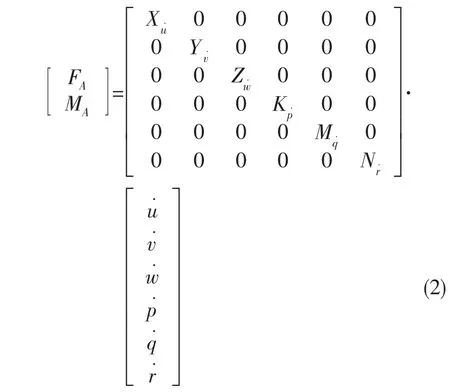
式中：u、v、w表示AUV速度在载体坐标系三个坐标轴的分量；p、q、r表示AUV角速度在载体坐标系三个坐标轴的分量，如图1所示；Xu˙、Yv˙、Zw˙表示与加速度相关的水动力系数；Kp˙、Mq˙、Nr˙表示与角加速度相关的水动力系数。

柯氏力和柯氏力矩可以表示为

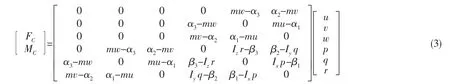
式中：m表示AUV本体的质量；Ix、Iy、Iz表示AUV本体相对于载体坐标系三个坐标轴的中心转动惯量，如表1所示；α1、α2、α3、β1、β2和β3可以表示为

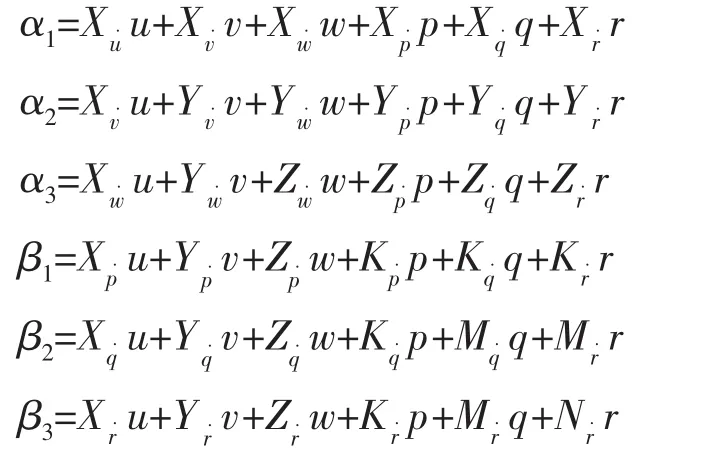
拖曳力和拖曳力矩分别为

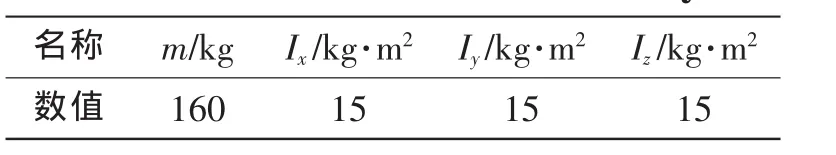
表1 AUV本体的参数Tab.1 Parameters of AUV body

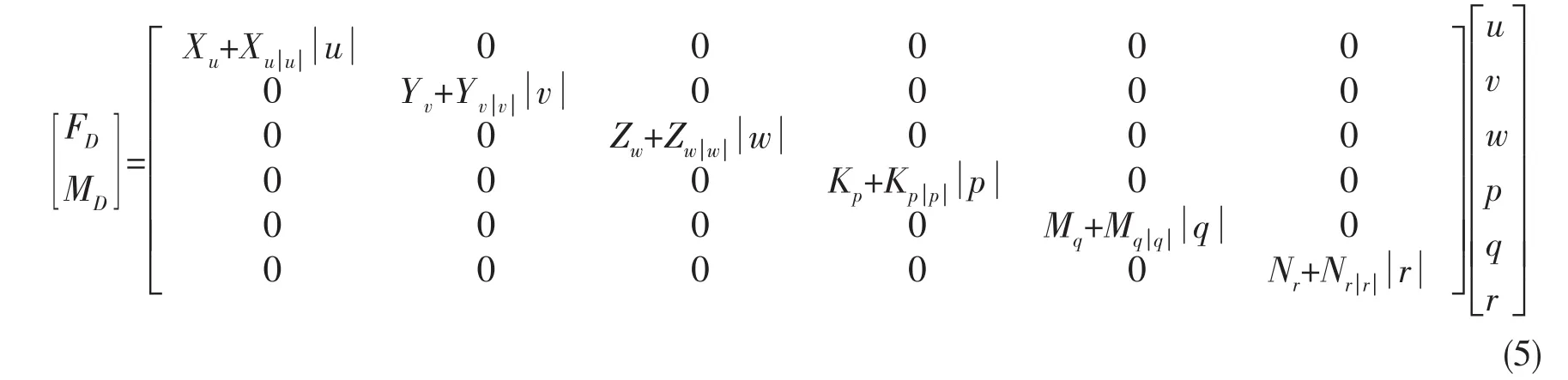
式中：Xu、Yv、Zw表示与速度相关的水动力系数；Kp、Mq、Nr表示与角速度相关的水动力系数；分别表示与相关的水动力系数。

有水流存在的情况下，AUV相对于水流的速度可以表示为

式中：uf、vf、wf为水流速度在载体坐标系三个坐标轴方向的分量。u′、v′、w′代替上述中的u、v、w即可获得水流作用下的水动力计算公式。

1.2 水动力系数

我们采用CFD软件设计AUV外形，通过Gambit导入AUV外形并对流体区域进行网格划分，最后将网格划分后的结果导入Fluent软件，设置边界条件，计算水动力系数。计算获得的水动力系数如表2～5所示，剩余水动力系数的取值为0。

表2 与速度相关的水动力系数Tab.2 Hydrodynamic coefficients associated with the velocity

表3 与速度的二次方相关的水动力系数Tab.3 Hydrodynamic coefficients associated with the square of the velocity

表4 与加速度相关的主要水动力系数Tab.4 The main hydrodynamic coefficients associated with the acceleration velocity

表5 与加速度相关的耦合水动力系数Tab.5 The coupling hydrodynamic coefficients associated with the acceleration velocity

2 运动学分析

本小节推导出AUV的速度、角速度、加速度、角加速度、偏速度和偏角速度的计算公式。速度对第r个广义速率求偏导数即可得到第r个偏速度，角速度对第r个广义速率求偏导数即可得到第r个偏角速度。为了便于描述我们引入Z函数。

2.1 广义坐标与广义速度

AUV可以等效为6自由度的刚体，因此，广义坐标可以定义为

式中：x0、y0、z0表示AUV质心在惯性坐标系中的位置；φ、θ、ψ表示AUV相对于惯性坐标系的姿态角。

广义速度可以定义为

本文用到两个坐标系：惯性坐标系和载体坐标系，如图1所示。两个坐标系之间可以通过坐标变换矩阵相互关联。从惯性坐标系到载体坐标系的变换矩阵可以表示为

式中：Z1=sinθ，Z2=cosφ，Z3=sinφ，Z4=cosθ，Z7=sinψ，Z9=cosψ。

2.2 运动学相关变量的计算

角速度可以表示为

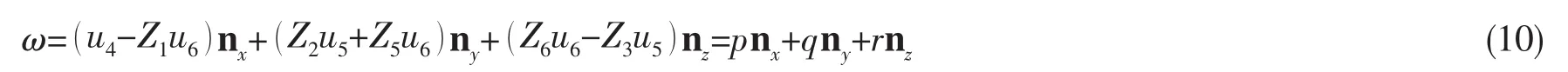
式中：nx、ny、nz为x、y、z轴方向的单位矢量；Z5=Z3Z4，Z6=Z2Z4。

AUV质心的速度可以表示为

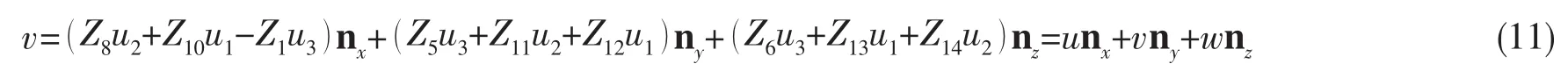
式中：Z8＝Z4Z7，Z10＝Z4Z9，Z11＝Z2Z9+Z1Z3Z7，Z12＝Z1Z3Z9-Z2Z7，Z13＝Z3Z7+Z1Z2Z9，Z14＝Z1Z2Z7-Z3Z9。

AUV上任意点的速度可以写成

式中：r为质心（载体坐标系原点）到任意点的矢径；（xa,ya,za）表示任意点在载体坐标系下的坐标。

角加速度为

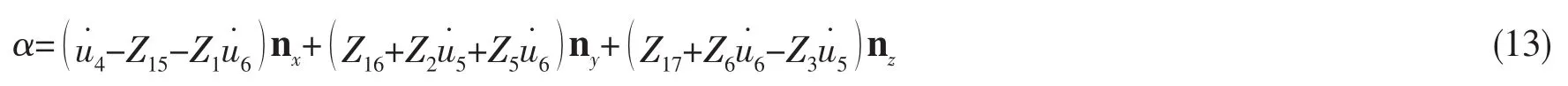
式中：Z15=Z4u5u6，Z16=Z6u4u6-Z3u4u5-Z1Z3u5u6，Z17=-Z2u4u5-Z1Z2u5u6-Z5u4u6。

加速度为

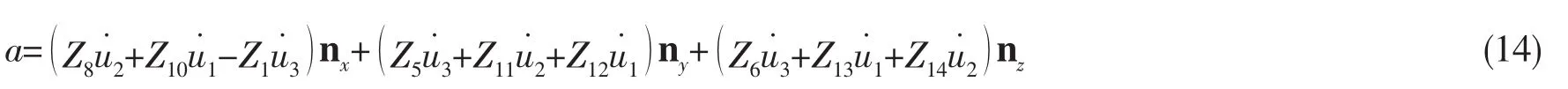
AUV上任意点的偏速度为

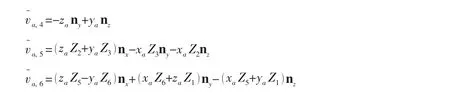
偏角速度为

3 动力学分析

本小结推导出基于凯恩动力学的AUV动力学方程。在推导过程中，首先计算出作用在AUV上的广义主动力和广义惯性力。作用在AUV上的力与作用点处的第r个偏速度点积，即可获得力对第r个广义主动力的贡献，力矩与第r个偏角速度求点积，即可得到力矩对第r个广义主动力的贡献。惯性力和惯性矩分别与偏速度和偏角速度求点积，即可得到惯性力和惯性矩对广义惯性力的贡献。

3.1 广义主动力和广义惯性力

作用在AUV上的力包括：惯性力F*、惯性矩T*、重力G、浮力B、附加质量力FA和附加质量矩MA、柯氏力FC和柯氏力矩MC、拖曳力FD和拖曳力矩MD、推进器的推力T1,T2,…,T6。惯性力、重力、附加质量力、柯氏力和拖曳力的作用点为质心，令（15）式中的xa=0，ya=0，za=0即可得到质心处的偏速度。同理，令（15）式中的xa、ya、za分别取浮心、推力作用点的坐标，即可得到浮心、推力作用点处的偏速度。

惯性力和惯性矩可以表示为

AUV本体对广义惯性力的贡献，可通过惯性力与质心处的偏速度点积、惯性矩与偏角速度点积获得。

重力对广义主动力的贡献为：

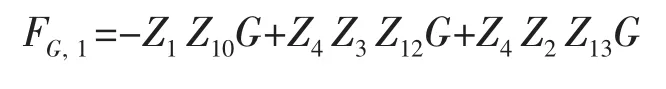
浮力对广义主动力的贡献为：

拖曳力和拖曳力矩对广义主动力的贡献为：

式中：FD,x、FD,y和FD,z为拖曳力在载体坐标系下的三个分量；TD,x、TD,y和TD,z为拖曳力矩在载体坐标系下的三个分量。

附加质量力和附加质量矩对广义主动力的贡献为：

柯氏力和柯氏力矩对广义主动力的贡献为：

推力对广义主动力的贡献为：

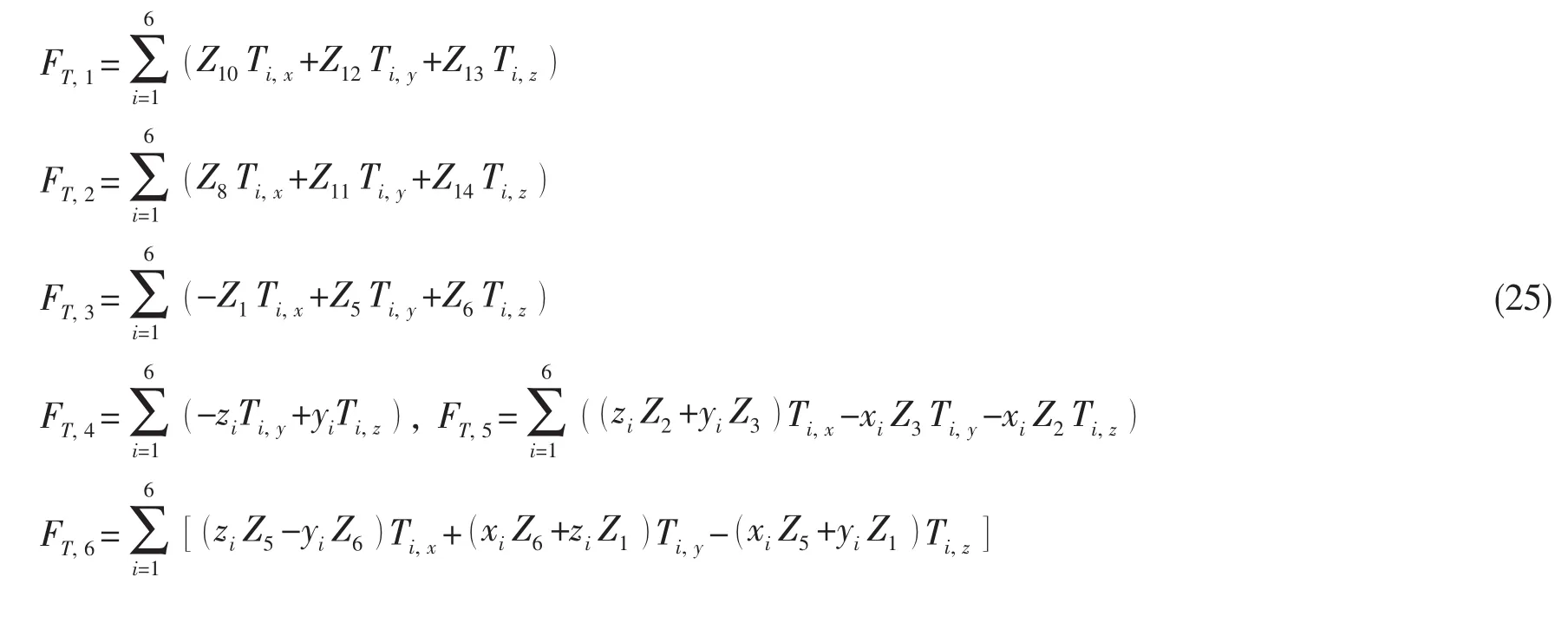
3.2 AUV凯恩动力学模型

AUV的凯恩动力学模型可以表示为

式中：

4 仿真验证

我们采用Matlab/Simulink中得S函数创建AUV凯恩动力学方程，在Simulink中设计AUV的控制系统，分别对AUV的深度控制（图2）和前进距离控制（图3）进行仿真。

由图2可以看出，0～16 s为AUV下潜的过程，16 s后，AUV达到期望的深度10m，并保持该深度不变。由图3可以看出，0～20 s为AUV前进的过程，20 s后，AUV达到期望的前进距离。仿真结果表明，我们创建的AUV模型是正确的。

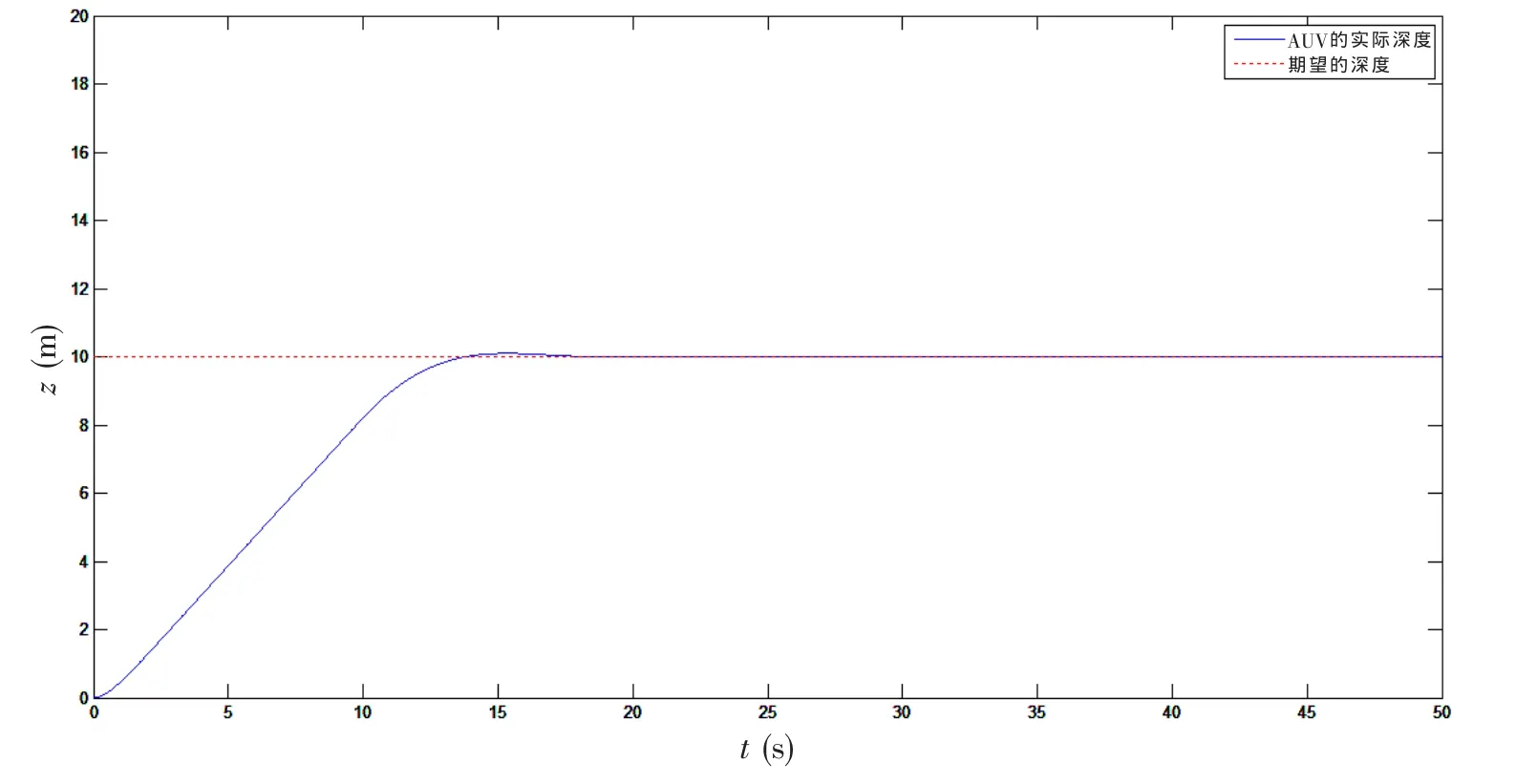
图2 AUV深度控制Fig.2 The deep control of AUV

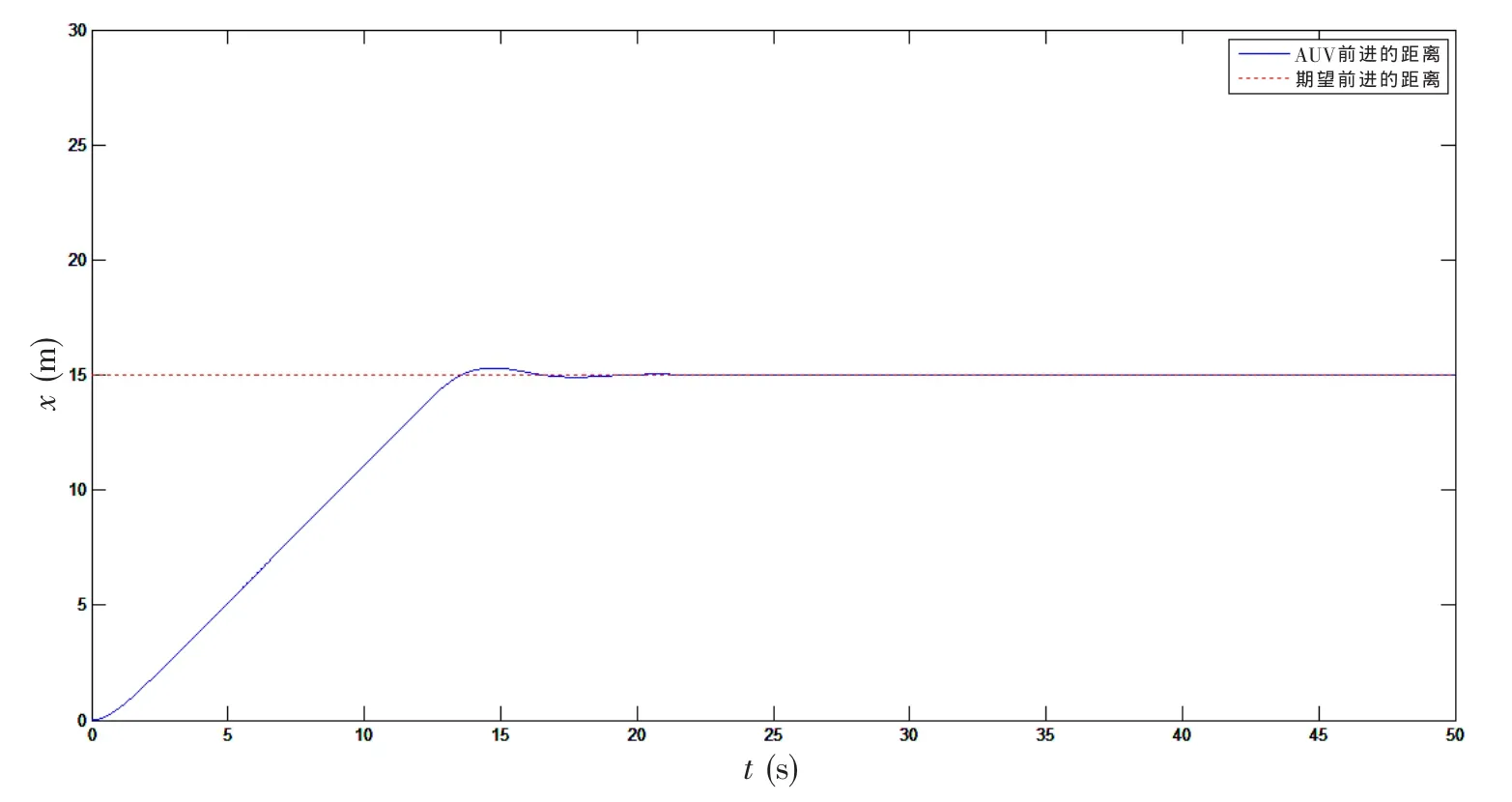
图3 AUV前进控制Fig.3 The forward control of AUV

5 结论

通过仿真实验，获得了AUV的水动力系数。详细介绍了基于凯恩动力学的AUV建模方法。通过该方法可以清晰地看出哪些力对AUV的动力学方程起作用。基于凯恩动力学建立的AUV模型，可以方便地转化成适用于控制的闭环形式。通过仿真，验证了基于凯恩动力学建立的AUV模型的有效性。

[1]管欣,张素民,詹军.基于凯恩方法的汽车悬架实时仿真模型[J].汽车工程,2010,32(8):649-653. Guan X,Zhang S M,Zhan J.A real-time simulation model for automotive suspension based on Kane’s method[J].Automotive Engineering,2010,32(8):649-653.

[2]孙占庚,金国光,常志,等.基于Kane方法的柔性机械臂系统动力学建模及其模态截取研究[J].天津工业大学学报,2009,28(4):61-63. Sun Z G,Jin G G,Chang Z,et al.Research of dynamic modeling of flexible manipulator system based on Kane’s method and its mode interception[J].Journal of Tianjin Polytechnic University,2009,28(4):61-63.

[3]Zhao D X.Dynamic analysis on a feeding and unloading manipulator using Kane’s method combined with screw theory[C]// Proceedings of the 2012 International Conference on Industrial Control and Electronics Engineering.Xi’an,China:IEEE, 2012:999-1002.

[4]Huang Y H,Liao Q Z,Wei S M,et al.Dynamics modeling and analysis of a front-wheel drive bicycle robot moving on a slope[C]//Proceedings of the 2010 IEEE International Conference on Automation and Logistics.Hong Kong,China:IEEE, 2010:43-48.

[5]Yang C F,Huang Q T,Ye Z M,et al.Dynamic modeling of a spatial 6-DOF parallel robots using Kane method for control purposes[C]//Proceedings of the 2010 2nd International Conference on Intelligent Human-Machine Systems and Cybernetics.Nanjing,China:IEEE,2010:180-183.

[6]Ge X F,Jin J T.Dynamics analyze of a dual-arm space robot system based on Kane’s method[C]//Proceedings of the 2010 2nd International Conference on Industrial Mechatronics and Automation.Wuhan,China:IEEE,2010:646-649.

[7]夏丹,陈维山,刘军考,等.基于Kane方法的仿鱼机器人波状游动的动力学建模[J].机械工程学报,2009,45(6): 41-49. Xia D,Chen W S,Liu J K,et al.Dynamic modeling of a fishlike robot with undulatory motion based on Kane’s method [J].Journal of Mechanical Engineering,2009,45(6):41-49.

[8]李新友,陈五一,韩先国.基于Kane方程的3UPS/S并联机构动力学研究[J].机床与液压,2011,39(13):1-5. Li X Y,Chen W Y,Han X G.Dynamic analysis of a 3UPS/S parallel mechanism based on Kane equations[J].Machine Tool and Hydraulics,2011,39(13):1-5.

[9]沈飞,曹志强,徐德,等.基于Kane方法的机器海豚动力学建模及速度优化方法[J].自动化学报,2012,38(8): 1247-1256. Shen F,Cao Z Q,Xü D,et al.A dynamic model of robotic dolphin based on Kane method and its speed optimization[J]. Acta Automatica Sinica,2012,38(8):1247-1256.

[10]Cheng G,Shan X L.Dynamics analysis of a parallel hip joint simulator with four degree of freedoms(3R1T)[J].Nonlinear Dynamics,2012,70(4):2475-2486.

[11]Liu X B.A Lie group formulation of Kane’s equations for multibody systems[J].Multibody System Dynamics,2008,20 (1):29-49.

[12]Yang K,Wang X Y,Ge T,et al.Dynamic model of underwater snake-like robot using Kane’s method[J].Journal of Shanghai Jiaotong University,2014,19(2):146-154.

[13]Yang K,Wang X Y,Ge T,et al.A dynamic model of an underwater quadruped walking robot using Kane’s method[J]. Journal of Shanghai Jiaotong University,2014,19(2):160-168.

Modeling of AUV based on Kane dynamics

SUN Jia-jie1,YANG Ke1,GE Tong2
(1.School of Mechanical Engineering,Hangzhou Dianzi University,Hangzhou 310018,China;2.School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiaotong University,Shanghai 200240,China)

Kinematics and dynamics for AUV are developed.The generalized active force and the generalized inertia force are deduced by means of replacing velocity and angular velocity by generalized velocity. The equations of hydrodynamic forces of AUV are deduced.Hydrodynamic coefficients are determined through simulation.The simulations of depth control and forward distance control are implemented to verify the dynamic model of AUV.Simulation results show that the dynamic model is effective.

Kane dynamics;AUV;model;generalized velocity

TP242.6

A

10.3969/j.issn.1007-7294.2017.08.004

1007-7294（2017）08-0960-08

2017-03-11

国家自然科学基金项目（51309133）；杭州电子科技大学科研启动基金项目资助（ZX150204301002/006）

孙佳杰（1998-），男，本科；杨柯（1983-），男，博士，讲师，E-mail:yjs2yangke@163.com。