基于灰色聚类权的车轴裂纹声发射信号风险评估

林 丽，许 强，周 勇

(1.大连交通大学 交通运输工程学院，大连 100240;2.大连理工大学, 大连 110023)

基于灰色聚类权的车轴裂纹声发射信号风险评估

林 丽1，许 强1，周 勇2

(1.大连交通大学 交通运输工程学院，大连 100240;2.大连理工大学, 大连 110023)

车轴是轨道车辆走行部的重要组成和连接部件，采用声发射技术监测车轴，运用灰色聚类的方法对车轴裂纹声发射信号进行风险评估，并与实际状态进行对比。结果表明，此方法在声发射信号风险评估领域具有一定的应用价值和可行性。

声发射信号；灰色聚类；风险评估

随着道路运输行业的飞速发展，铁路车辆也进入了一个大发展的新阶段[1]。在轨道车辆上，车轴是机车车辆走行部轮轴系统的重要组成部分，是转向架轮对中重要的部件之一，其质量直接影响到车辆运行的安全性。

声发射(Acoustic Emission，AE)也称应力波发射，指结构或材料局部因能量快速释放而发出瞬态弹性波的现象[2-3]，是新型的无损检测手段[4-5]。相较于其他方法，声发射检测技术不仅抗干扰能力强，而且能够在低速轻载下诊断轴承的故障。THEODORE等[6]对声发射信号进行包络解调，通过分析频谱来监测轴承应力和工作状态，验证了该方法的可靠性和有效性。曲文生等[7]利用声发射参数分析和小波分析手段对海洋平台材料弯曲疲劳损伤过程进行分析，得到了损伤过程中不同阶段的特征信息，为声发射技术在海洋平台安全监测中的应用提供了理论支持。

对于声发射信号的风险评估，目前进行的研究还较少。邹兵等[8]利用声发射检测技术结合FLUENT软件模拟，探讨了气体阀门内漏过程中的声发射参数分布规律。李伟等[9]对T300碳纤维复合材料板拉伸断裂过程进行了声发射监测，应用K-means聚类判定了T300碳纤维复合材料板拉伸断裂信号的失效形式，并对该聚类模型进行了有监督的训练和测试，将其应用到相似的未知损伤信号中，很好地完成了模式识别。在轨道车辆上，张庆宇[10]利用VAR模型对车轴的声发射信号进行风险预测。杨时川[11]利用模糊综合分析法对车轴实时监测的声发射信号进行风险评估，判断车轴的风险等级。目前，通过声发射信号分析来确定车轴裂纹状态进而完成风险评估的方法中，主要有模特卡罗法、故障树法、模糊层次分析法以及向量自回归模型法等。模特卡罗法需要构建含有相互影响关系的自变量的功能函数，可将声发射数据通过LMD分解为几个具有相互关系的因变量，但是功能函数的构建没有统一标准，得不到结果值，所以不能区分裂纹状态。对于故障树法，分解出来的PF分量是平级的，很难构建上下级关系，所以也不能判断车轴裂纹状态。模糊层次分析法是将得到的试验数据，由专家小组打分并计算转化成可以评估的数值，进而完成裂纹状态的评估；其具有一定的主观性，有时不能准确地区分车轴实时裂纹状态。张庆宇的向量自回归模型法虽然预测了车轴的裂纹状态，但并没有很好的结果来区分以及评估出车轴裂纹状态[10]。

1982年，邓聚龙提出了灰色系统理论，该理论以少数据不确定系统为研究对象来获得有用信息，探究各信息因素之间的行为、规律、影响等，通过数学关系建立相应的模型[12]。灰色聚类是根据灰色关联矩阵或灰数的白化权函数将一些观测指标或观测对象聚集成若干个可定义类别的方法。灰色聚类评估在水电工程、航空航天、桥梁、气象、机械等领域有广泛应用。

贾立敏等[13]运用物理-事理-人理系统方法论(WSR)和灰色聚类综合法对水电工程建设过程中的进度风险因素进行了3个维度以上的分类，确定工程的风险等级并找出了风险度较大的因素。张峰等[14]运用灰色聚类评估模型对舰载机系统进行安全评估，在预防和降低事故发生方面起到了积极作用。庞伟英等[15]利用灰色聚类法的主观与客观计算相结合的评价方法对大跨径桥梁施工阶段的风险进行安全评估，确定了综合风险等级。金灿灿等[16]运用SDG模型推理得到各种故障序列，并将其看作灰色系统，用灰色聚类决策对这些序列进行风险评估，解决了风险评估过程中评价指标和属性值难以确定和量化、风险分析和评估缺乏系统性和一致性的问题。

1 灰色聚类方法在声发射故障风险评估中的研究

灰色聚类评估模型在风险评估中被广泛应用，包括在变压器、气轮发动机等故障风险评估中的应用。前人的研究虽然与笔者研究的理论模型相同，但应用的方式和领域等都有所不同：首先，他们并非在声发射信号领域的应用；其次，与其他研究者选取的评价指标类型不同，笔者根据试验获取信号，并对信号进行特征分析，然后以这些能够表现信号故障的特征信号作为评价指标，从而能更直观地判断风险等级。而其他研究者选取的评价指标大多为影响各自研究对象的因素。

李爱民等[17]在基于灰色熵权聚类决策的机械故障诊断中，对某型船齿轮箱在运行中的不同状态进行检测，提取12组不同状态样本特征频段的能量作为特征参数，结合熵权灰色聚类进行风险评估。他的研究虽然也是针对车轴实时信号，以不同频段的故障特征作为指标参数对灰色聚类模型进行风险评估的，但笔者首先针对的是声发射信号领域，目前针对声发射信号的灰色聚类评估研究甚少；其次，李爱民仅用了一个特征参数——特征频段的能量，而笔者用了能量、均值、峭度、功率共4个特征参数作为灰色聚类模型的指标参数进行综合评估，以研究灰色聚类评估在声发射信号领域的可行性。

2 灰色聚类理论基本原理

2.1 灰色定权聚类概念

(1)

式中：ηj为对象i属于灰类k的灰色定权聚类系数。

灰色定权聚类即为根据灰色定权聚类系数的值对聚类对象进行归类。

2.2 基于中心点三角白化权函数的灰色评估模型

基于三角白化权函数的灰色评估方法是刘思峰教授在1993年提出的，此模型是一种评估数量和信息对象少的模型，此方法在近几年被广泛运用于各类评估实践中。基于中心点三角白化权函数改进了基于端点三角白化权函数存在两个以上灰类重叠交叉的缺点。笔者也将利用此方法对列车车轴声发射信号进行风险评估。

基于中心点三角白化权函数的灰色评估方法在划分灰类时，将属于该灰类程度最大的点划分为该灰类的中心点。

该方法假设有n个对象，m个评估指标，s个不同的灰类，且设定对象i关于指标j的样本观测值为xij(i=1,2,3,…,n;j=1,2,…,m)，这样便可通过xij的值对相应的对象进行评估、诊断。以下是基于中心点三角白化权函数的灰色评估模型的基本计算步骤[12]。

(1) 评估灰类划分。按照评估要求所需划分灰类数s，分别确定灰类1，2，…，s的中心点(中心点是最可能属于某一灰类的点，它可以是对应小区间的中点，也可以不是中点)；将各个指标的取值范围也相应地划分为s个灰类，分别以λ1，λ2，λ3，…，λs作为各个灰类的代表。

(2) 将灰类向不同方向进行延拓，考虑增加0灰类和s+1灰类，并确定其中心点λ0，λs+1，从而得到新的中心点序列λ0，λ1，λ2，λ3，…，λs，λs+1。

图1 中心点三角白化权函数示意

对于指标j的一个观测值x，可由式(2)计算出其属于灰类k(k=1，2，…，s)的隶属度。

(2)

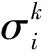
(3)

3 基于灰色聚类权的车轴裂纹声发射信号风险评估

3.1 风险评估数据的获取

文章用于评价车轴风险的数据是声发射信号,取笔者所在课题组试验所得的声发射信号为试验数据进行验证[18]，来判断此方法是否可行。该信号采样频率为106Hz,采样点数为4 096个。

通过试验监测车轴在运行过程中不同状态的声发射信号。收集了车轴在运行过程中从产生轻微裂纹到裂纹扩大至极具毁坏性裂纹的九组信号样本。样本中的状态不同，有的是小裂纹产生时的状态，有的是中裂纹产生时的状态，还有的是大裂纹产生时的状态，如图2所示。

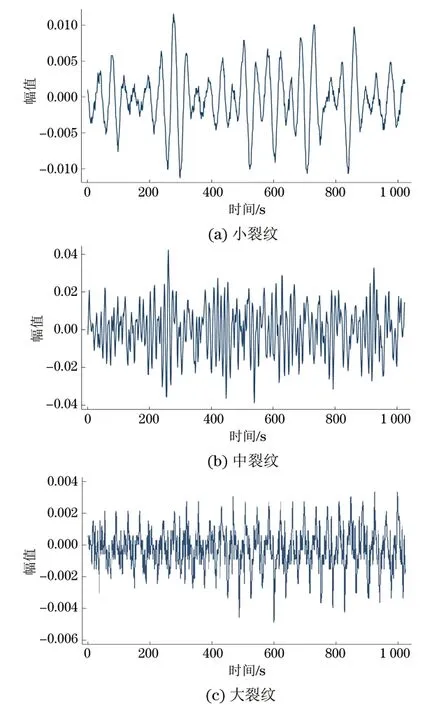
图2 三种裂纹状态下的声发射信号波动图

从图2中可看出：从小裂纹到大裂纹的发展过程中，信号的波动频率是逐渐增大的，而波动幅值是先增加后减小的。

3.2 构建评价指标

笔者在前人研究的基础上，综合考虑后选用均值、峭度值、能量值和功率值等作为车轴风险评估的4个评价指标。

3.3 数据处理

笔者通过对试件的在线监测试验，获得了9组不同故障阶段的车轴声发射信号样本。为了进一步评价其风险等级，必须先计算出各个信号的评价指标的参考值，根据选择的评价指标进行数据处理。

因此，笔者首先在MATLAB平台上，利用MATLAB软件编写相关代码计算小裂纹、中裂纹、大裂纹等共9组数据样本的均值、峭度值、能量值和功率值4个评价指标因素。

如表1所示，ni(i=1,2,…,9)为样本；m为评估指标(m1表示均值指标，m2表示峭度值指标，m3表示能量值指标，m4表示功率值指标)；c为样本状态(1表示小裂纹，2表示中裂纹，3表示大裂纹)。

表1 车轴声发射信号状态参数

3.4 车轴故障声发射信号的风险等级灰类的划分 为了尝试对车轴故障风险等级评估进行研究，在数据获取时按照故障从小到大取了3个频段的数据，因此根据表1计算得到的4个评价指标的参考值确定灰类的中点，在划分灰类时按照需求划分1，2，3三个灰类，分别为低风险、中风险、高风险。S1，S2，S3作为各个指标的取值范围的相应3个灰类，以其作为各个灰类的代表。对于灰类中心点的选取是最可能属于某一灰类的点，其可以是对应小区间的中点，也可以不是中点。根据表1的特征参数值，为了尽可能地使其处于合理的灰类范围内，笔者选用近似黄金分割法来划分白化分界值，以9组数据的各个评价指标参数的平均数作为中间值，高的白化分界值为中间分界值提高60%得到，低的分界值为中间分界值降低40%得到。表2所示为划分灰类的风险等级及阈值中心点。

表2 划分灰类的风险等级及阈值中心点

3.5 车轴故障声发射信号评价指标的延拓值 对于车轴声发射信号的故障风险的各评价指标,将其灰类中心点向左、右不同方向进行延拓，以表2中相邻阈值差的平均值作为差值，确定各个指标的延拓值，如表3所示。

表3 评价指标的延拓值

通过对表2和表3的整理，总结出灰色聚类评价模型的中心点序列λ0，λ1，λ2，λ3，λ4,以便于建立中心点三角白化权函数。整理出的中心点序列如表4所示。

表4 灰色评价模型的中心点序列

3.6 车轴故障声发射信号的白化权函数表达式

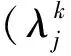
对于指标j的一个观测值x，当k=2,3，…,s-1时，可有下式：

(4)

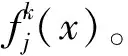
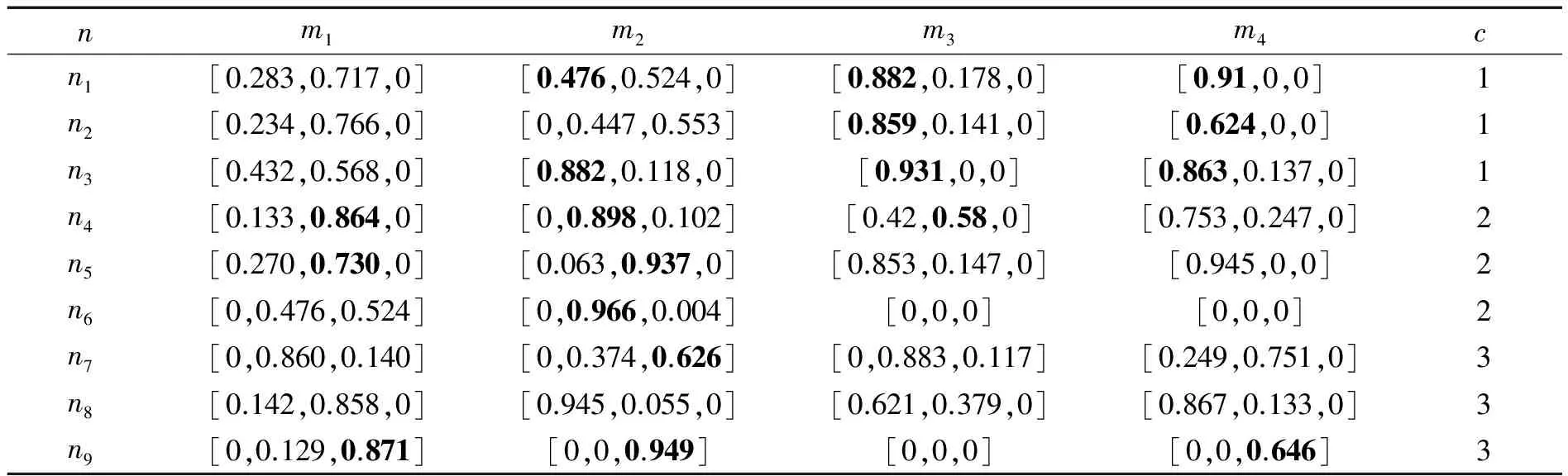
表5 样本信号对应各指标的隶属度

表5中为9个样本声发射信号的均值、峭度、能量、功率4个指标的隶属度值。表中的c为样本信号原始的状态参数；1表示小裂纹，2表示中裂纹，3表示大裂纹，对应着灰类的低风险、中风险和高风险。表5中加粗的隶属度表示对应的灰度与原始信号状态相一致的样本信号与指标，从表中可初步判断，36组隶属度中有18组与已知状态相一致，其中m1即均值指标有3组，m2即峭度值指标有7组，m3即能量值指标有4组。m4即功率值指标有4组，因此，由此判断4个指标在后期求综合聚类系数的权重，权重为各指标与原始信号状态一致的组数与总共状态一致的组数的商，由此可得η1=0.17，η2=0.39，η3=η4=0.22。

表6 评估结果与真实状态的比较

4 结论

(1) 利用灰色聚类的中心点三角白化权函数评估方法对试验获取的9组不同状态的车轴故障声发射信号的评估结果与真实状态进行比较，评估结果的正确率为78%。

(2) 在9组信号的灰色中心点三角白化权函数评估中，有7组是与真实状态相一致的，78%的正确率可以说明灰色聚类的中心点三角白化权函数评估对声发射信号的风险评估是可行的。

(3) 采取能够表现车轴声发射信号故障的4个参数作为指标，比单指标评估更为合理。

(4) 灰色聚类权的中心点三角白化权函数评估方法的中心点序列和求综合聚类系数的权重的选取略有些主观性。

[1] 严隽耄,傅茂海.车辆工程[M]. 北京:中国铁道出版社,2012.

[2] TAN C K, MBA D. Identification of the acoustic emission source during a comparative study on diagnosis of a spurgearbox[J].Tribology International,2005,38(5):469-480.

[3] MIRHADIZADEH S A,MONCHOLI E P,MBA D.Influence of operational variables in a hydrodynamic bearing on the generation of acoustic emission[J].Tribology International,2010,43(9):1760-1767.

[4] TITTMANN B R,YEN C E.Acoustic emission technique for monitoring the pyrolysis of composites for process control[J].Ultrasonics,2008,48(6/7):621-630.

[5] MBA D,RAO R B K N.Development of acoustic emission technology for condition monitoring and diagnosis of rotating machines:bearings,pumps,gearboxes,engines and rotating structures[J].The Shock and Vibration Digest,2006,38(1):3-16.

[6] THEODORE G,WILLIM H,MARTIN K. Acoustic emissions in broadband vibration as an indicator of bearing stress[J]. Aerospace Conference Proceedings, 2000,6(3):95-122.

[7] 曲文声,王寿军,穆为磊,等. 基于声发射技术的海洋平台材料疲劳损伤检测[J]. 无损检测,2016,38(10):10-13.

[8] 邹兵,贾招弟,李伟. 基于声发射技术的气体阀门内漏诊断[J]. 无损检测,2016,38(3):56-59.

[9] 李伟,李英年,蒋鹏,等. T300碳纤维复合材料损伤声发射信号的有监督模式识别[J]. 无损检测,2016,38(2):9-13.

[10] 张庆宇. 基于模型轨道车辆车轴声发射风险评估[D].大连：大连交通大学,2014.

[11] 杨时川. 车轴声发射信号VAR和ARMA预测及风险层次分析[D]. 大连：大连交通大学,2015.

[12] 刘思峰,杨英杰,吴利丰.灰色系统理论及其应用[M].北京:科学出版社,2014.

[13] 贾立敏,王巧珍,向想想,等.基于WSR-灰色聚类综合法的水电工程进度风险评估[J].水力发电,2014,40(12):83-86.

[14] 张峰,汪鹏为,肖支荣,等.灰色理论在舰载机系统安全评估中的应用[J].飞机设计,2010,30(3):56-61.

[15] 庞伟英,樊燕燕,李红,等.基于灰色聚类法的大跨径桥梁施工阶段风险评价[J].工程管理学报,2015,29(2):101-105.

[16] 金灿灿,王海燕,左洪福,等. 基于SDG和灰色聚类的系统故障风险评估方法[J].系统工程理论与实践,2015,35(4):1048-1056.

[17] 李爱民,刘国庆.基于灰色熵权聚类决策的机械故障诊断[J].舰船科学技术，2011，3(7):125-127.

[18] LI Lin, CHU Fulei. HHT-based AE characteristics of natural fatigue cracks in rotating shafts[J]. Mechanical Systems and Signal Processing, 2012, 26:181-189.

The Risk Assessment about Axle Crack Acoustic Emission Signals Based on the Grey Cluster Method

LIN Li1, XU Qiang1, ZHOU Yong2

(1.Dalian Jiaotong University, School of Traffic and Transportation Engineering, Dalian 100240, China; 2.Dalian University of Technology, Dalian 110023, China)

Axle rail vehicle bogie is an important part and a connecting part. Acoustic emission technique was employed to monitor the axle, and the grey clustering method was used to evaluate the risk of axle crack acoustic emission signals and was compared with the actual state. The results show that this method has certain application value and is feasible in the field of acoustic emission signal.

acoustic emission signal; grey cluster; risk assessment

2016-05-16

国家自然科学基金资助项目(51275066)；湖南科技大学机械设备健康维护湖南省重点实验室开放基金资助项目(201401)

林 丽(1971-),女，副教授，主要从事列车故障监测诊断研究工作

林 丽,173670324@qq.com

10.11973/wsjc201708013

TG115.28

A

1000-6656(2017)08-0051-06