单臂临床试验生存分析的样本量估计
2017-08-21张秀萍赵耐青
张秀萍 赵耐青
(复旦大学公共卫生学院生物统计学教研室 上海 200032)
单臂临床试验生存分析的样本量估计
张秀萍 赵耐青△
(复旦大学公共卫生学院生物统计学教研室 上海 200032)
目的 提出并验证单臂临床试验进行生存分析时的样本量估计方法。方法 通过理论公式的推导,得到单臂临床试验进行生存分析时样本量估计的计算公式,并采用STATA软件进行蒙特卡洛随机模拟,估计实际的检验效能,从而验证公式的准确性。结果 随机模拟结果表明在α=0.025和α=0.01的情况下,用本文提出的公式计算得到的样本量模拟得到的检验效能与预设的检验效能基本一致。结论 在单臂临床试验中利用本文的公式计算得到的样本含量能够达到预定的检验效能。本研究的成果为抗肿瘤药物的早期临床研究的样本量估计提供了可靠的依据。
单臂临床试验; 样本量估计; 生存分析
单臂临床试验是指在进行临床试验时,只设立一个试验组,而不设立平行对照组。这种试验设计方法常用于药物研发的早期阶段(如Ⅰb/Ⅱa期)。在抗肿瘤药物的临床研究中,需要初步探索药物的有效性与安全性时,一般采用单臂临床试验[1]。以肿瘤药物临床试验为例,单臂临床试验需要设定中位生存期的目标值,如果研究人群的中位生存期超过中位生存期的目标值,则可以认为该研究药物的疗效优于目标值。
尽管随机对照临床试验是临床试验设计的金标准,但不是所有的临床试验都可以做到这一点,如果所研究的患病人群很小,或该药物的研发是一项突破性的进展,或所研究的药物需求度很高,则可以选择进行单臂临床试验。FDA的研究数据显示,1992年12月1日至2010年7月1日期间,美国FDA对35种抗肿瘤药物的47个新适应证进行了加速审批,其中28个是基于单臂临床试验设计[2]。2005年之后,FDA批准的申请中,随机对照试验与单臂临床试验的比例为1∶1[3]。我国也有依据单臂临床试验结果批准注册的案例,如克唑替尼、依维莫司等[1]。
在临床试验设计阶段,可靠地估算所需的样本量是一个至关重要的问题。目前文献中只提出了随机对照临床试验样本量的估算方法[4],还没有关于单臂临床试验进行生存分析的样本量计算公式。因此,本文主要阐述单臂临床试验设计下进行生存分析所需样本量的估计方法,并给出假设检验的模拟结果。
资 料 和 方 法
指数分布在生存分析中占据着重要的地位,它是历史上第一个生存时间分布模型,也是最简单、最重要的分布。指数分布是一种纯随机失效模型,指研究对象在任何时间上的风险函数为一常数,即风险函数的大小不受生存时间长短的影响,是一种“无记忆的分布”[5]。
(1)
假定病例收集时间为[0,T],病例随访时间截止到T+τ,任何一个符合研究条件的患者进入该单臂临床试验的时间为随机变量x,假设x在[0,T]内服从均匀分布,则受试者在[x,T+τ]期间死亡的概率为:
(2)
则受试者在研究期间[0,T+τ]上的死亡概率为:
(3)
将(3)代入公式(1),可以得出:
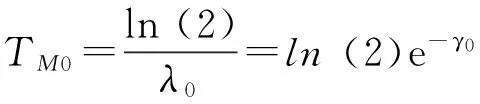
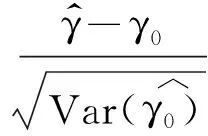
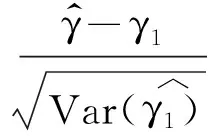
(4)
进而推导出样本量的计算公式为:
(5)
其中,Zα、Zβ为标准正态分布下的分位数。
λ0:基于生存时间服从指数分布,且中位生存时间为目标值所对应的风险率;
λ1:基于生存时间服从指数分布的研究人群的实际风险率;
T:收集受试者的时间段为[0,T];
τ:停止收集受试者后随访的时间长度;
TM0:研究目标值的中位生存时间;
TM1:研究人群的中位生存时间;
α:犯第一类错误的概率;
β:犯第二类错误的概率。
对于估算的样本量,进行随机模拟检验其检验效能 我们运用蒙特卡洛方法进行随机模拟,首先利用计算机的随机函数,在[0,T]产生服从均匀分布的伪随机数x1,x2,…,xn(用x1,x2,…,xn模拟n个受试者进入单臂临床试验的时间点)。同理,在[0,1]上产生均匀分布的伪随机数,然后用对数函数将其转化为服从指数分布的伪随机数t1,t2,…,tn(用t1,t2,…,tn模拟n个受试者的生存时间),设随访时间为[T,T+τ],则整个研究期间为[0,T+τ]。若xi+ti≤T+τ,表示第i个受试者在研究期间死亡,则其生存结局d=1;反之,表示第i个受试者在研究结束时仍然存活,为截尾数据。假设研究目标值的中位生存期为TM0,研究人群的中位生存时间为TM1,收集病例的时间为T,随访时间为τ,用计算机模拟产生数据,再用STATA软件作生存分析的指数回归模型拟合,并进行假设检验。用无效假设H0被拒绝的比例作为检验效能的估计值。
结 果
我们分别随机模拟了在显著性水平α=0.025和α=0.01的情况下不同预定检验效能1-β所对应的单侧拒绝率,即在两种不同的研究背景下,用计算机分别产生1 000个相同样本含量的模拟数据样本且每个样本均符合设定条件,再计算这1 000个样本所对应的1 000个生存分析指数回归模型拟合的参数检验中,无效假设H0被拒绝的比例,并用这个比例作为该检验效能的估计。
研究背景及参数设置 研究背景1:研究目标值的中位生存时间TM0为10个月,研究人群的中位生存时间TM1为13个月,收集病例的时间T为12个月,停止收集病例后的随访时间τ为24个月。
研究背景2:研究假设的中位生存时间TM0为9个月,研究人群的中位生存时间TM1为12个月,收集病例的时间T为18个月,停止收集病例后的随访时间τ为24个月。
模拟结果 表1分别给出了研究背景1、2在显著性水平α=0.025的情况下不同预定检验效能1-β所对应的单侧拒绝率模拟结果;表2分别给出了研究背景1、2在显著性水平α=0.01的情况下不同预定检验效能1-β所对应的单侧拒绝率模拟结果。
由表1、2的随机模拟结果可以看出,在显著性水平α保持不变的情况下,预期的检验效能1-β越高,根据公式估计得到的样本含量越大;同理,当其他参数都固定不变的前提下,显著性水平α越低,根据公式估计得到的样本含量也越大。通过计算机模拟产生样本,对病例的中位生存时间进行假设检验,得到各组单侧拒绝率的估计值与预定的检验效能都比较接近。
讨 论
样本量的估计是临床试验设计中极为重要的一个环节,只有达到充足的样本量,才能够保证有足够的把握度来发现实际存在的差异。本文经随机模拟,表明在α=0.025和α=0.01的情况下,各预定的检验效能1-β与单侧拒绝率估计值比较接近,因此该样本量估算的公式是有效和可靠的。
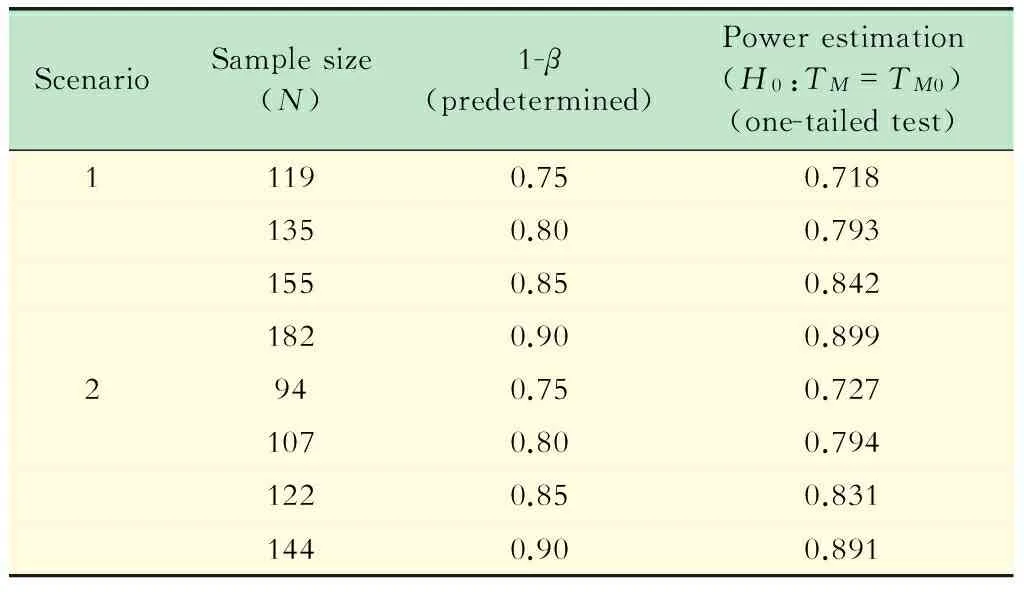
表1 α=0.025时不同预设1-β情况下的样本量与检验效能估计
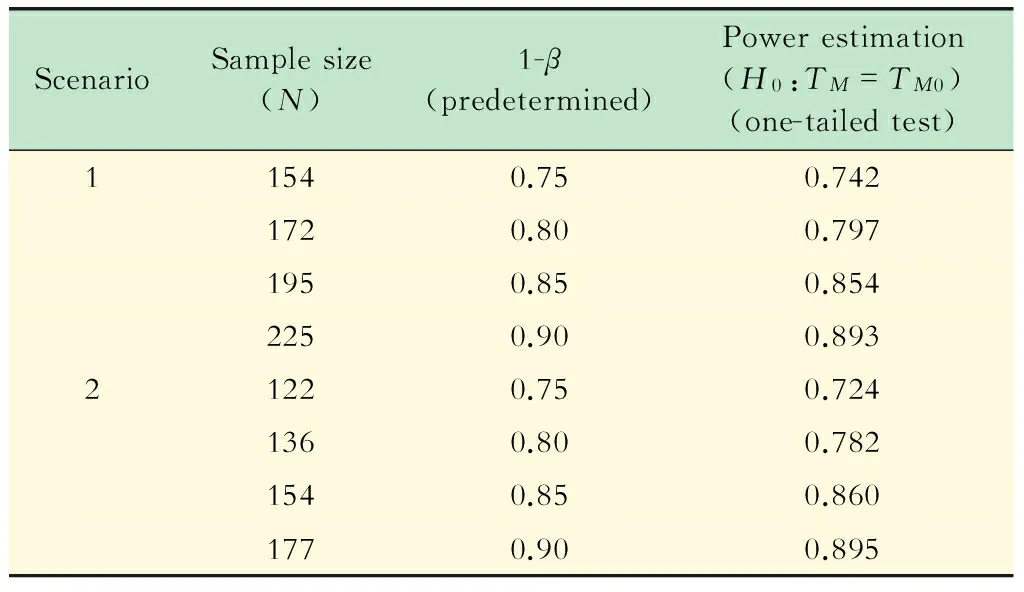
表2 α=0.01时不同预设1-β情况下的样本量与检验效能估计
由于生存时间往往是偏态的,不适用基于正态分布理论的统计学方法,而指数分布是生存分析中最简单与最重要的分布,所以我们在拟合生存资料的数据时,是基于生存时间服从指数分布进行推导的。同时,本文所推导的单臂临床试验生存分析的样本量估计公式采用的是正态近似法,所以当研究假设的中位生存时间与研究人群的中位生存时间相差过大时,该公式计算得到的样本量就会变小,则正态近似的方差就会变大,导致检验效能的下降。
单臂临床试验有其特定的优点,即所有的受试者都接受同一种试验药物,试验设计、实施趋于简单、易行,且研究周期较III期临床试验短[6];但其缺点也显而易见,由于使用试验药物的受试者与历史对照数据在基线特征、诊断标准等方面可能存在一定的差异,可比性差,所以要谨慎选择历史对照数据,对其可靠性进行充分评价[1]。但该试验设计在新药研发中有其特定的地位,若所研究的疾病为非常严重的或罕见的疾病,目前尚无适合的治疗药物,同时根据研究药物的作用机制、动物试验、以及早期的经验,可以推荐所研究的新药时,在探索性阶段可以使用单臂临床试验。
随着创新药物研发的不断活跃,新的药物和治疗手段不断产生,无论是国内还是国外,采用单臂研究设计开展注册研究的越来越多[1],但目前尚没有单臂临床试验设计下进行生存分析的样本量估算公式。本文给出了该类研究的样本量估算的推导过程及公式,可使研究者在设计此类试验时计算样本量更加方便和准确,在实际的临床试验中有一定的推广意义。
[1] 张虹,高晨燕,陈晓媛,等.关于采用单臂临床试验数据用于支持进口药品注册的考虑[J].中国新药杂志,2013,22(18):2126-2129.
[2] JOHNSON JR,NING YM,FARRELL A,etal.Accelerated approval of oncology products:the food and drug administration experience[J].JNatlCancerI,2011,103(8):636-644.
[3] ELLENBERG SS.Accelerated approval of oncology drugs:can we do better?[J].JNatlCancerI,2011,103(8):616-617.
[4] 李婵娟,蒋志伟,王锐,等.随机对照药物临床试验样本量估计[J].中国临床药理学与治疗学,2011,16(10):1132-1136.
[5] LEE ET.生存数据分析的统计方法.2版[M].北京:中国统计出版社,1998:156-161.
[6] JUNG SH.Statistical issues for design and analysis of single-arm multi-stage phase II cancer clinical trials[J].ContempClinTrials,2015,42:9-17.
Sample size estimation for survival analysis in single-arm trials
ZHANG Xiu-ping, ZHAO Nai-qing△
(DepartmentofBiostatistics,SchoolofPublicHealth,FudanUniversity,Shanghai200032,China)
Objective To propose a method to calculate sample size for survival analysis in single-arm trials. Methods Through theoretical formula derivation,we provided sample size estimation method for survival analysis in single-arm trials.Monte-Carlo simulations using STATA software were conducted to obtain the empirical power,so as to verify the accuracy of the estimated sample size.Results Simulation results showed that,whenα=0.025 andα=0.01,the power of the sample size calculated by the formula is in accordance with the predetermined power. Conclusions The formula of sample size estimation we proposed could achieve the predetermined power for survival analysis in single-arm trials.Findings of this study provide reliable basis for sample size estimation of early stage antineoplastic drug clinical studies.
single-arm trials; sample size estimation; survival analysis
国家自然科学基金(81273187)
R195.1
A
10.3969/j.issn.1672-8467.2017.04.022
2017-02-14;编辑:张秀峰)
△Corresponding author E-mail:nqzhao@126.com
*This work was supported by the National Natural Science Foundation of China (81273187).
