反射法测量三棱镜顶角实验中三棱镜摆放位置研究
2017-08-20刘雪华丛红璐王林杰马俊刚成爽吕
刘雪华+丛红璐+王林杰+马俊刚+成爽+吕金钟

【摘要】经过理论分析和实验验证,讨论反射法测量三棱镜顶角的实验中,三棱镜在载物台上的一定范围内的上下平移对测量结果的影响,得出此平移范围的上下限。并对左右平移范围作出分析。
【关键词】三棱镜顶角 分光计 平移位置
【基金项目】河北省创新能力提升计划软科学研究及科普专项项目(17K55304D);教育部高等学校物理类专业教学指导委员会力学教学改革项目(JZW-16-LX-07);河北省高等学校科学技术研究青年基金项目(QN2017101);河北省实验教学示范中心建设项目;北京交通大学海滨学院校级教学改革项目(HBJY16010,HBJY16004)资助。
【中图分类号】O435 【文献标识码】A 【文章编号】2095-3089(2017)29-0165-02
测量三棱镜顶角是研究三棱镜折色率及色散特性的重点,实验上常利用分光计测量光线偏转角度间接测量三棱镜的顶角。分光计测三棱镜顶角常用的方法有自准直法和反射法[1]。本文重点讨论反射法测量三棱镜顶角时,三棱镜摆放位置对测量结果的影响。
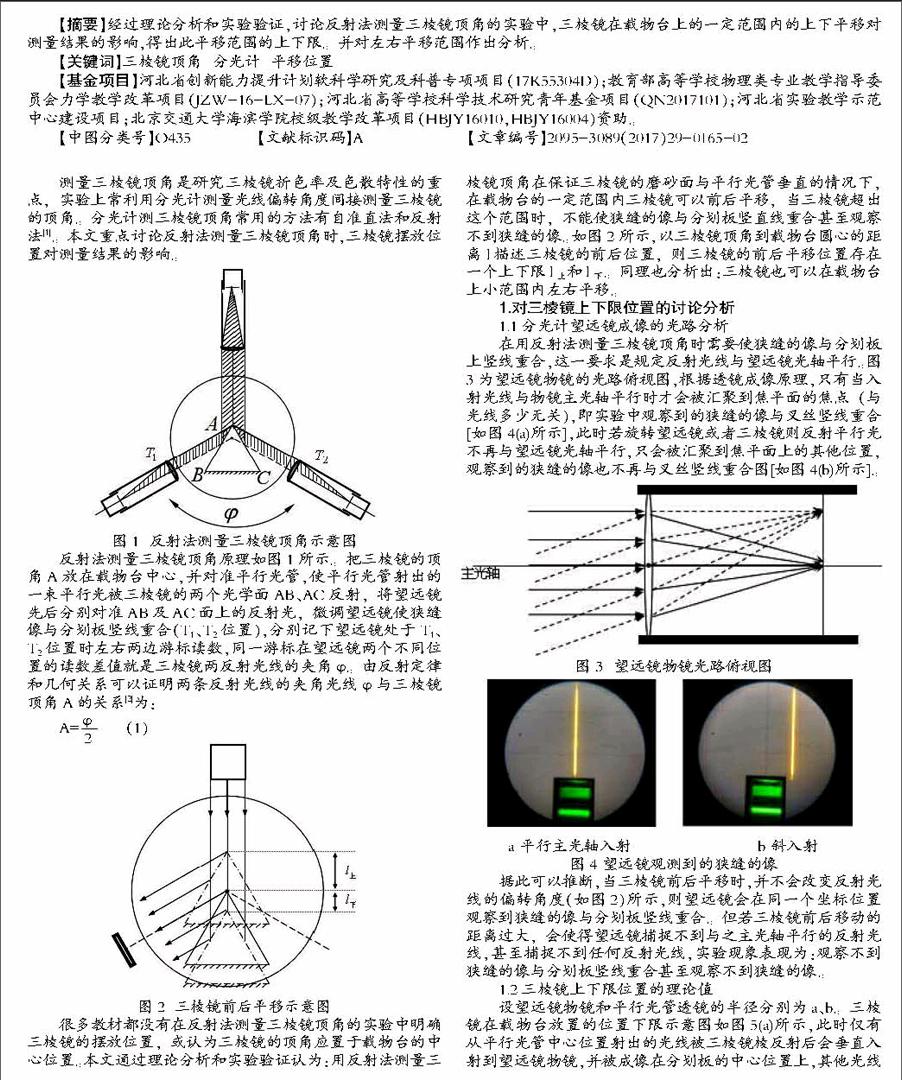
反射法测量三棱镜顶角原理如图1所示。把三棱镜的顶角A放在载物台中心,并对准平行光管,使平行光管射出的一束平行光被三棱镜的两个光学面AB、AC反射,将望远镜先后分别对准AB及AC面上的反射光,微调望远镜使狭缝像与分划板竖线重合(T1、T2位置),分别记下望远镜处于T1、T2位置时左右两边游标读数,同一游标在望远镜两个不同位置的读数差值就是三棱镜两反射光线的夹角?渍。由反射定律和几何关系可以证明两条反射光线的夹角光线?渍与三棱镜顶角A的关系[2]为:
A=■ (1)
很多教材都没有在反射法测量三棱镜顶角的实验中明确三棱镜的摆放位置,或认为三棱镜的顶角应置于载物台的中心位置。本文通过理论分析和实验验证认为:用反射法测量三棱镜顶角在保证三棱镜的磨砂面与平行光管垂直的情况下,在载物台的一定范围内三棱镜可以前后平移,当三棱镜超出这个范围时,不能使狭缝的像与分划板竖直线重合甚至观察不到狭缝的像。如图2所示,以三棱镜顶角到载物台圆心的距离l描述三棱镜的前后位置,则三棱镜的前后平移位置存在一个上下限l上和l下。同理也分析出:三棱镜也可以在载物台上小范围内左右平移。
1.对三棱镜上下限位置的讨论分析
1.1分光计望远镜成像的光路分析
在用反射法测量三棱镜顶角时需要使狭缝的像与分划板上竖线重合,这一要求是规定反射光线与望远镜光轴平行。图3为望远镜物镜的光路俯视图,根据透镜成像原理,只有当入射光线与物镜主光轴平行时才会被汇聚到焦平面的焦点(与光线多少无关),即实验中观察到的狭缝的像与叉丝竖线重合[如图4(a)所示],此时若旋转望远镜或者三棱镜则反射平行光不再与望远镜光轴平行,只会被汇聚到焦平面上的其他位置,观察到的狭缝的像也不再与叉丝竖线重合图[如图4(b)所示]。
据此可以推断,当三棱镜前后平移时,并不会改变反射光线的偏转角度(如图2)所示,则望远镜会在同一个坐标位置观察到狭缝的像与分划板竖线重合。但若三棱镜前后移动的距离过大,会使得望远镜捕捉不到与之主光轴平行的反射光线,甚至捕捉不到任何反射光线,实验现象表现为:观察不到狭缝的像与分划板竖线重合甚至观察不到狭缝的像。
1.2三棱镜上下限位置的理论值
设望远镜物镜和平行光管透镜的半径分别为a、b。三棱镜在載物台放置的位置下限示意图如图5(a)所示,此时仅有从平行光管中心位置射出的光线被三棱镜棱反射后会垂直入射到望远镜物镜,并被成像在分划板的中心位置上,其他光线虽被三棱镜反射但反射光线不能射入望远镜。根据图5(b)所示的几何关系,可以得出此时三棱镜顶角距离载物台圆心的下限距离为:
l下=■ (2)
图6(a)为三棱镜在载物台放置位置上限的示意图,此时仅有从平行光管边缘位置射出的光线被三棱镜棱AB和AC面反射后会垂直入射到望远镜,并成像在分划板的中心位置上,其他光线虽被三棱镜反射但反射光线不能射入望远镜。根据图6(b)所示的几何关系,可以得出此时三棱镜距载物台圆心的上限距离为:
l上=■+■·■=■ (3)
2.实验验证
2.1实验步骤及测量
本实验采用JJY型分光计,调整好分光计使得平行光管能发出平行光,望远镜能接收平行光,望远镜和平行光管的光轴及载物台的台面均与分光计中心轴垂直[3] 。将三棱镜放置在已调平的载物台上,调节三棱镜使其磨砂面垂直于平行光管主光轴,使顶角与载物台圆心的距离为l,向左旋转望远镜直至找到狭缝的像并使之与望远镜分划板竖线重合(T1位置),记录游标读数(?兹1和?兹2);再向右转动望远镜直至再次找到狭缝的像并使之与望远镜分划板竖线重合(T2位置),记录游标读数(?兹'1和?兹'2)。结合(1)式可得三棱镜顶角计算式:
A=■(?兹'1-?兹1+?兹'2-?兹2) (4)
保持三棱镜磨砂面与平行光管主轴垂直,竖直方向平移三棱镜(即改变l),重复上述步骤测量。
2.2实验数据及数据分析
表1列出的是不同l(三棱镜顶角A在O上方为正,下方为负)值下,望远镜在T1、T2位置观测到狭缝的像与分划板竖线重合时对应的游标读数。
从该表可看出在保证三棱镜的磨砂面与平行光管的主光轴垂直的情况下,三棱镜在一定范围前后平移时望远镜的位置读数误差小于2',利用(4)式计算出来的三棱镜顶角值几乎没有变化,这一结论与笔者理论分析一致。实验中还发现,当l<-10.78mm和l>24.16mm时,狭缝的像颜色已经很淡,几乎找不到狭缝的像。
本实验所用分光计望远镜半径b=11.98mm、平行光管半径a=11.98mm,载物台直径D=69.80mm棱镜的顶角近似以A=π/3计算,根据(2)、(3)式可求出三棱镜前后摆放位置的理论极限值:l下=13.83mm,l上=27.67mm。
实验得到的三棱镜顶角A距离载物台圆心下限距离l=10.78<13.83mm,上限距离l=24.16<27.67mm。实验值略小于理论值,分析主要原因,其一在于当三棱镜在临界位置附近时,只有很少的光线能进入望远镜,狭缝的像颜色非常浅,人眼很难分辨,第二个原因在于,在测量平行光管透镜和望远镜物镜的直径时,由于仪器结构原因,不能十分准确测量a,b,由此导致我们计算所得的三棱镜前后摆放位置的理论极限值与实验测得的极限值有差异。
3.三棱镜左右限位置的理论值思考
根据1.1光路分析结果,可以很容易分析出當三棱镜左右平移时,也不会改变放射光线的偏转角度,但若三棱镜左右移动的距离过大,会使得望远镜捕捉不到与之主光轴平行的反射光线,甚至捕捉不到任何反射光线,实验现象表现为:观察不到狭缝的像与分划板竖线重合甚至观察不到狭缝的像。
如图1所示,此时从平行光管射出的平行光左半部分被AB面反射后可以全部垂直入射望远镜,右半部分被AC面反射后可以全部垂直入射望远镜,在此位置三棱镜向左平移最大位置为l左=a/2(此时仅有从平行光管左侧边缘位置射出的光线被三棱镜棱AB面反射后会垂直入射到处于T1位置的望远镜物镜),同理向右平移的最大位置为l右=a/2。
当三棱镜处于1.2讨论的下限位置时(如图5a),三棱镜若向左平移则望远镜在T2位置捕捉不到任何反射光线,观测不到与分划板竖线重合的狭缝的像,若向右平移则望远镜在T1位置观测不到与分划板竖线重合狭缝的像。
当三棱镜处于1.2讨论的上限位置时(如图6a),三棱镜像左平移则望远镜在T1位置捕捉不到任何反射光线,观测不到与分划板竖线重合的狭缝的像,若向右平移则望远镜在T2位置观测不到与分划板竖线重合狭缝的像。
4.结束语
通过理论分析和实验验证,得出三棱镜顶角距载物台中心距离的上下限理论值分别为:l上=(a+b)/sin A和l下=b/sin A。对三棱镜左右平移的极限值位置作了简单思考。综合全文,利用分光计使用反射法测量三棱镜顶角的实验中,三棱镜在小范围内上下左右平移,并不会对实验结果造成影响。
参考文献:
[1]隗群梅.关于测量三棱镜顶角的两种方法比较[J]大学物理实验,2010,23(1):41-42.
[2]丁慎训,张连芳.物理实验教程[M].北京:清华大学出版社,2002:202-212.
[3]吕金钟.大学物理实验教程[M].7版.北京:北京交通大学出版社,2012:60-61.
作者简介:
刘雪华(1983-),女,辽宁辽阳人,北京交通大学海滨学院讲师,硕士,主要从事大学物理与大学物理实验教学研究工作。
