感应电动机参数选择对动态无功需求的影响

游雨琛，张 妍

（广东工业大学自动化学院，广东 广州 510006）

感应电动机参数选择对动态无功需求的影响

游雨琛，张 妍

（广东工业大学自动化学院，广东 广州 510006）

针对电动机负荷在故障恢复过程中无功需求大幅度增长的问题，以单机带负荷系统为研究对象，采用感应电动机负荷和静态负荷并联构成的负荷模型，利用电磁暂态仿真软件PSCAD/EMTDC,通过改变电动机负荷比例、电动机参数等方法，探讨综合负荷在出现扰动之后的动态响应特性。分析结果表明：在相同负荷水平下，含水泵的综合负荷模型无功需求增长幅度最大，系统存在功率失稳风险。

综合负荷模型；感应电动机；电力系统；电压稳定性

电力系统动态仿真分析对电网的设计规划和调度运行具有重要作用，元件模型的合理性直接影响仿真结果的准确性。随着电网规模不断发展扩大，现有的发电机和线路的模型较为成熟，系统的动态响应也越来越复杂，负荷建模问题受到广泛关注［1-3］。

电力系统综合负荷中，感应电动机的负荷所占比例较高，约60%～70%，在工业负荷中所占的比例更高。感应电动机的动态特性对电网暂态电压稳定性产生了显著影响，动态负荷精确建模是研究电压稳定性的重要环节［4］。目前感应电动机综合负荷模型应用较为广泛，建模仿真是研究负荷特性的主要手段，但负荷参数出现偏差将导致仿真结果偏离实际情况［3-4］。通过对实测数据进行辨析可以获得较为准确的负荷参数，但考虑到操作难度较大，往往选择采用典型参数代替。

目前涉及对典型电动机参数进行分析的文献较少，不同类型的电动机参数对系统产生的具体影响尚不明确，因此本文旨在研究8种典型参数在暂态过程中呈现的动态无功特性以及对系统功率稳定性的影响，为选择恰当的感应电动机参数提供参考依据，避免出现负荷特性与实际不符导致分析结果不准确的情况发生。

1 研究现状及存在的问题

1.1 研究现状

负荷是电力系统不可或缺的组成部分，其动态特性直接决定了仿真结果是否准确［5-6］。

文献［7］认为静态负荷模型不能反映系统电压变化期间引起的功率需求变化，采用动态负荷模型的仿真结果更为合理。文献［8］通过计算分析表明电动机负荷比例对系统的静态电压稳定存在明显影响，电动机负荷比例增大，系统静态电压稳定性变差。文献［9］指出动态负荷模型与静态负荷模型在动态无功需求特性方面差异较大，不同的动态负荷模型参数对其动态响应特性造成的差异显著。

文献［10］对常用的3种感应电动机综合负荷模型进行分析比较，指出三阶机电暂态模型能较为准确地反映感应电动机负荷的动态特性，但计算量较大；一阶机械模型的动态有功响应比较准确，动态无功响应存在偏差；一阶电压暂态模型的动态无功计算结果精度高，有功功率计算结果误差很大。文献［11］通过定性分析指出感应电动机的参数在动态过程中对其功率的需求产生的影响，认为定子电阻和激磁电抗对感应电动机的功率特性无明显影响，转子电阻数值的大小与无功需求增长速率成反比。文献［12］基于某实际系统进行小干扰稳定性分析，总结了感应电动机模型各个参数对系统稳定性的影响规律，其普遍性有待深入研究验证。

1.2 存在的问题

过往有关负荷特性的研究通常只注重研究方法和模型的正确性，忽略了负荷参数的重要性。由于负荷参数不准确将导致分析结果偏乐观或者偏保守，使系统安全运行存在风险或在规划设计上增加不必要的建设成本。

目前电气和电子工程师协会（IEEE）以及中国电力科学研究院（CEPRI）已经推荐了多种典型感应电动机参数，不同类型的参数在动态响应上是否存在大幅度的差异、对系统功率稳定性是否存在影响值得探究。本文的研究工作主要包括呈现相同负荷条件下各种典型电动机参数的动态功率特性，对现有的典型参数进行初步评定，为选择电动机负荷参数提供指引。

2 综合负荷模型的功率特性

负荷是电力系统的一个重要组成部分，根据模型是否反映负荷的动态特性可以将其分为动态态模型和静态模型。

2.1 静态负荷功率特性

静态负荷［13-14］部分不考虑频率变化，负荷功率与节点电压的关系为

式中：PL、QL—表示静态负荷吸收的有功和无功；

PL0、QL0、VL0—分别为静态负荷吸收的有功、无功功率以及负荷母线的电压；

V—负荷母线的实际电压；

系数ap、bp、cp、aQ、bQ、cQ—分别表示恒阻抗、恒电流和恒功率部分在静态负荷中有功功率以及无功功率的比例，并且满足以下关系

结合式（1）、（2）可知静态负荷在电压跌落后的恢复过程中，负荷的功率需求变化和负荷母线电压恢复趋势基本一致，不能反映感应电动机等动态负荷在恢复过程中需要从电网吸收大量无功的现象，但只采用静态负荷模型将会使计算误差过大［15］。

2.2 动态负荷功率特性

综合负荷模型中的动态负荷部分通常由感应电动机模型组成［16］，动态负荷功率特性是基于感应电动机负荷模型展开的。

目前计算精度最高的是五阶电磁暂态模型，模型考虑了定子和转子的电磁暂态特性以及转子的机械特性，实际应用中常根据分析计算的精度要求对模型进行简化［17］。当不考虑定子的电磁暂态特性时，即可得到三阶机电暂态模型。现有的感应电动机三阶机电暂态模型具有较好的计算精度，能较为准确地反映暂态过程中的动态响应，文献［6］给出的直角坐标形式为

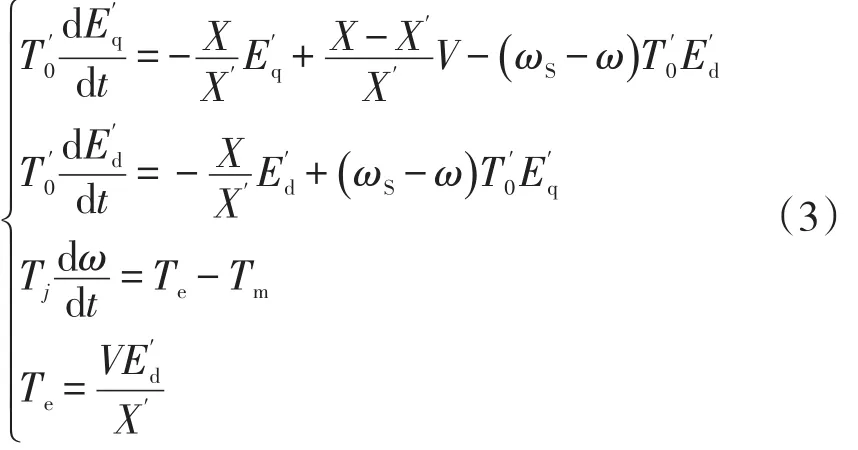
式中变量均为标幺值。

X′、X—分别为暂态电抗、同步电抗；

ω—转子转速；

Tj—惯性时间常数；

Te、Tm—分别为电磁转矩、机械转矩；

V—负荷母线端电压；

ωs—系统角频率。

在三阶机电暂态模型基础上，如果进一步忽略转子绕组的暂态特性，只考虑转子的机械暂态，就可获得感应电动机的一阶机械暂态模型，其等值电路［18］如图1所示。

图1 感应电动机等值电路

根据图1可得感应电动机的等值阻抗ZIM(s)为

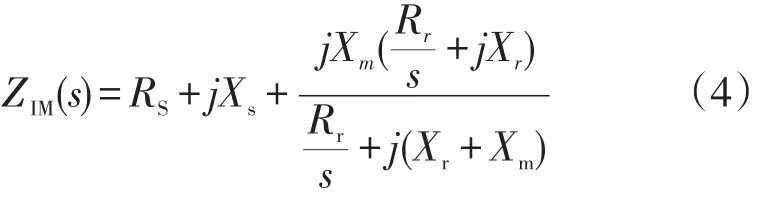
因此一旦转子和定子相关参数确定后，感应电动机的等值阻抗变成了关于转子滑差s的函数，令ZIM(s)=RIM(s)+jXIM(s)展开后可得：

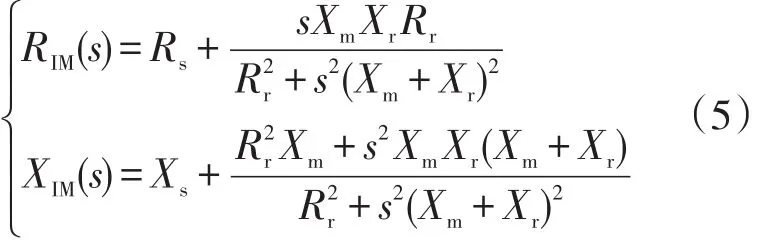
式中：RIM(s)—感应电动机的等值电阻；

XIM(s)—感应电动机的等值电抗。

在标幺值形式下电动机消耗的有功功率PIM和无功功率QIM分别为：

分析负荷的功率特性是准确建模的基础［19］，根据式（4）、（5）、（6）可绘制出感应电动机的阻抗-滑差特性以及功率-滑差特性曲线，如图2所示。

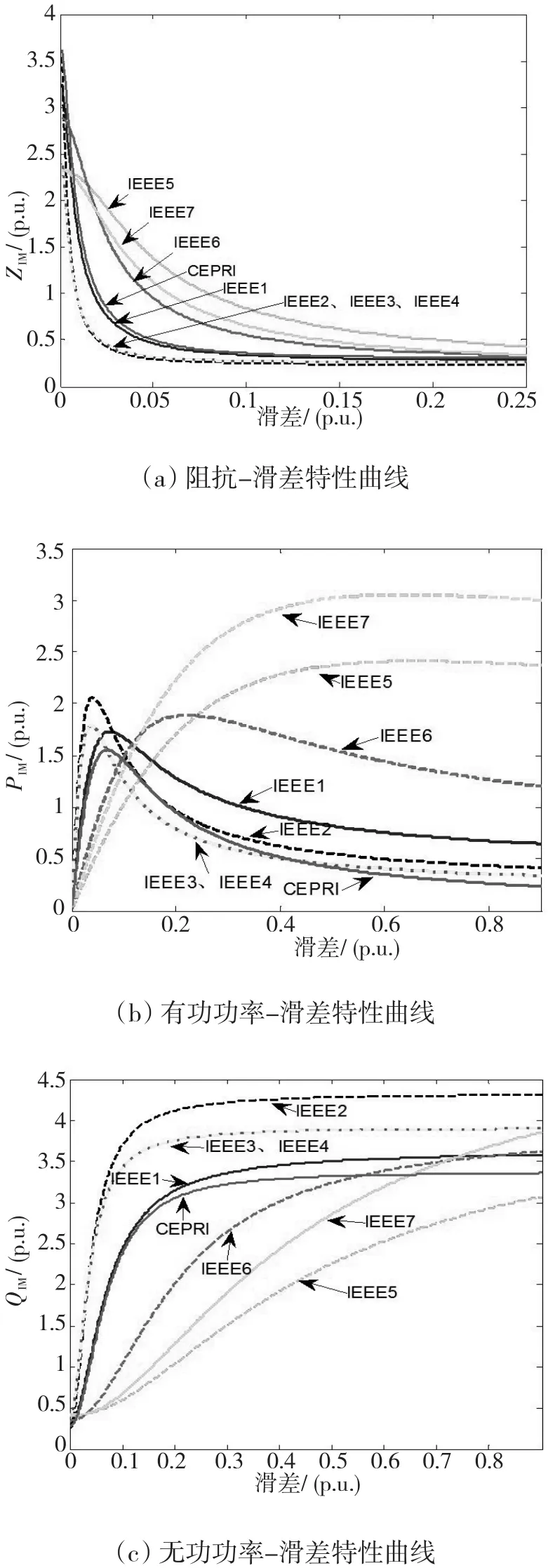
图2 感应电动机动态特性

文献［5］中IEEE以及CEPRI推荐的参数［5］属于常用的感应电动机模型参数，见表1。结合文献［5-7］可知IEEE推荐的7种参数：IEEE1-IEEE7依次分别代表：小型工业、大型工业、水泵、电厂辅机、民用综合、工业与民用综合以及空调综合的感应电动机模型。

表1 IEEE和CEPRI推荐的感应电动机参数

从图2可以看出，大型工业感应电动机和水泵模型的功率需求对转子滑差的灵敏度较高，临界滑差较小。民用综合和空调综合的感应电动机功率特性比较平缓，滑差增大时无功功率需求增加速率慢，动态无功峰值较低，系统恢复到稳态所需时间较短。

综上可知，相同负荷水平条件下，不同类型的电机参数的初始滑差存在较大差距，当运行滑差大于临界滑差时，将导致系统功率稳定性下降，负荷的功率需求需要更长时间才能恢复到正常水平。因此，模型参数选择不当可能导致暂态仿真结果偏保守或偏乐观，甚至失去参考意义。

2.3 仿真验证

在PSCAD环境中搭建图3所示的简单电力系统，不考虑同步发电机的动态特性［20］，其中Eeq为电源的等值电量变压器T容量SN=100 MVA，Vs%=13%，变比为10.5/121 kV，单回线路等值阻抗为1.6+j7.2（Ω），综合负荷功率为40+j20（MVA），感应电动机负荷占比60%，剩余部分负荷采用恒阻抗负荷进行仿真。

图3 简单电力系统

选用IEEE7型电动机参数，分别在20%和60%电动机负荷以及恒阻抗负荷的情况下设置其中一回输电线路末端发生三相短路接地故障，持续时间0.2 s，仿真结果如图4所示。

将感应电动机负荷比例维持60%，负荷母线发生0.2 s三相短路接地故障，分别用表1的8种参数进行仿真，图5是综合负荷动态响应的仿真结果。

图4 不同感应电动机负荷比例的仿真结果

图5 不同感应电动机参数的动态响应结果

分析图4可知，感应电动机负荷比例越高，暂态过程中综合负荷从电网吸收的有功、无功功率峰值越大，不同比例的电动机负荷将导致仿真结果出现大幅度的差异。

在相同负荷水平的情况下，根据图5可以发现IEEE3水泵模型的动态无功功率峰值约为IEEE5民用综合感应电动机模型的3倍，所需的恢复时间更长，存在功率失稳的趋势，由参数类型变化引起的动态功率需求差异不可忽略。

3 效果评价

上述仿真算例将8种典型参数的动态功率响应结果以曲线形式呈现出来，直观地反映了由参数类型变化引起的响应差异明显。根据图5的综合负荷动态无功响应曲线可以将8组参数分为3大类：乐观型参数、保守型参数以及临界型参数。

乐观型参数指IEEE5、IEEE6、IEEE7参数，这类参数的功率特性对滑差的灵敏度低，暂态过程中的无功响应变化较平缓。

保守型参数指IEEE1、IEEE2、IEEE4和CEPRI参数，采用这类参数的电动机在暂态过程中从电网吸收的无功功率较多，可达到乐观型参数的2倍。

临界型参数指IEEE3参数，采用该组参数在暂态过程出现的动态无功峰值最高，所需的恢复时间最长，同时存在功率失稳的趋势，放大了扰动对系统的影响程度。

针对不同研究目的，在选择电动机参数时应进行相应的调整。当工业负荷比例较高的片区进行建模仿真时，推荐选择保守型电动机参数；当对民用负荷区域进行暂态稳定性分析时，推荐选择乐观型参数；当对供电可靠性要求较高的片区进行可靠性验证时可选用临界型参数。

4 结论

（1）本文通过理论分析和仿真算例呈现出IEEE和CEPRI推荐的8种典型参数的负荷功率特性，在相同的系统环境下得到的仿真结果具有可比性和参考意义。

（2）文中的算例均采用电磁暂态仿真工具PSCAD/EMTDC进行，能较为准确地还原综合负荷的动态特性并获得具有一定精度的计算结果。

（3）电力系统规划、设计和运行都离不开仿真，对常用的电动机典型参数进行分类能为参数选择提供参考依据，根据研究对象选择参数有助于提高仿真结果的准确性。

（4）仿真结果表明电动机参数类型变化将导致其动态无功需求出现大幅度的变化，对系统的稳定性存在不可忽略的影响。

（5）目前的负荷模型还停留在较为粗糙的阶段，本文基于现有的典型参数对负荷可能出现动态功率响应特性进行了分析，仅仅指出了由参数选择引起的问题，构建负荷模型和参数辨析的研究工作还有待进一步完善。

［1］ 段献忠,张广恕.负荷建模研究现状综述[J].电力系统自动化,1994,18(8):60-66.

［2］ 孙华东,周孝信,李若梅.感应电动机负荷参数对电力系统暂态电压稳定性的影响[J].电网技术,2005,29 (23):1-6.

［3］ 张景超,鄢安河,张承学,等.电力系统负荷模型研究综述[J].继电器,2007,35(6):83-88.

［4］ Borghetti A,Caldon R,Mari A,et al.On dynamic load models for voltage stability studies[J].IEEE Transac⁃tions on Power Systems,1997,12(1):293-303.

［5］ 贺仁睦.电力系统动态仿真准确度的探究[J].电网技术,2000,24(12):1-4.

［6］ 徐泰山,薛禹胜,韩祯祥.关于电力系统电压稳定性分析方法的综述[J].电力系统自动化,1996,20(5):62-67.

［7］ 张红斌,李黎,贺仁睦.动静态负荷模型在电网暂态稳定计算中的应用[J].电力自动化设备,2003,23(6): 49-53.

［8］ 任杰桢,鞠平,赵娟,等.考虑电动机负荷的静态电压稳定分析[J].电力自动化设备,2014,34(5):139-143.

［9］ 张一荻,管霖.负荷模型选择对动态无功需求和暂态电压稳定的影响[J].广东电力,2014,27(9):49-54.

［10］鞠平,潘学萍.3种感应电动机综合负荷模型的比较[J].电力系统自动化,1999,23(19):40-42.

［11］赵健,郑超,王爱渌,等.感应电动机功率特性及其对电压稳定的影响机制[J].智能电网,2014,10:005.

［12］李桂红,韩肖清.感应电动机负荷参数及运行状态对电力系统小干扰稳定性的影响[J].电力学报,2010, 25(2):131-134.

［13］何仰赞,温增银.电力系统分析(下册)[M].武汉：华中科技大学出版社,2002.

［14］王锡凡,方万良,杜正春.现代电力系统分析[M].北京：科学出版社,2003.

［15］王卫国,贺仁睦.反映综合负荷动特性机理的感应电动机模型[J].电力系统自动化,2002,26(4):23-27.

［16］李佳,刘天琪,李兴源,等.感应电动机模型和机械转矩参数对暂态电压稳定评估的影响[J].电力系统保护与控制,2014,42(12):19-24.

［17］李欣然,贺仁睦.负荷特性对电力系统静态电压稳定性的影响及静态电压稳定性[J].中国电机工程学报, 1999,19(4):26-30.

［18］Aung M T,Milanovic J V.Analytical assessment of the effects of voltage sags on induction motor dynamic re⁃sponses[C]//Power Tech,2005 IEEE Russia.IEEE, 2005:1-7.

［19］孙华东,周孝信,李若梅.计及感应电动机负荷的静态电压稳定性分析[J].中国电机工程学报,2005,25 (24):1-7.

［20］李立理,陆超.综合负荷模型的电动机参数独立性分析和主导参数选取[J].电力系统自动化,2009(13): 22-26.

［21］赵兵,汤涌.感应电动机负荷的动态特性分析[J].中国电机工程学报,2009(7):71-77.

Influence of parameter selection of induction motor on dynamic reactive power demands

YOU Yuchen，ZHANG Yan
(School of Automation,Guangdong University of Technology,Guangzhou Guangdong 510006,China)

Aiming at the problem of the reactive power demands in motor load large increasing during the fault recovery,takes the single unit load system as the research subject，adopts the load model consisted of induction motor load and static load parallel,utilizes electromagnetic transient simulation software PSCAD/EMTDC,by changing the load proportion and motor parameters,discusses the comprehensive load dynamic response characteristic after the disturbance appearing.The analysis result shows that under the same load level,the reactive power demands increase of comprehensive load model containing the water pump is the largest,so the system exists the risk of power unsteadiness.

composite load model;induction motor;power system;voltage stability

TM34

A

1672-3643（2017）03-0045-06

10.3969/j.issn.1672-3643.2017.03.009

2017-03-18

游雨琛，（1982），男，工学硕士，研究方向为电力系统稳定分析与控制。

有效访问地址：http://dx.doi.org/10.3969/j.issn.1672-3643.2017.03.009