汽车ABS逻辑门限控制及仿真*

方春杰

（重庆交通大学）

高速行驶的汽车在行驶方向上遇到突发状况时，需要进行紧急制动，但当前后车轮均位于低附着系数路面时，不能充分利用制动系统提供的制动力，前后车轮极易发生抱死，从而造成制动效能下降，汽车的制动距离大幅度增加。汽车防抱死系统（ABS）可以在低附着系数路面上制动时防止车轮发生完全抱死，提高汽车的转向操纵能力以及方向稳定性，缩短制动距离[1-2]120-121。文章以制动工况下的汽车为研究对象，建立单轮汽车系统动力学模型，并分析ABS控制原理，建立ABS逻辑门限控制模型，对制动工况的汽车进行控制，在Simulink中搭建仿真模型并进行离线仿真，仿真结果表明：该控制方法可以保证制动过程中车轮最佳滑移率，使汽车具有良好的制动效能，缩短制动距离，提高汽车行驶的安全性。

1 单轮汽车系统动力学建模

1.1 单轮汽车系统制动模型

为了反映汽车在制动工况下车轮的运动状态以及动力学特性，建立单轮汽车系统制动模型[3]44，如图1所示。

图1 单轮汽车系统制动模型图

根据牛顿第二定律，建立单轮汽车系统制动模型的动力学方程，如式（1）所示。

式中：m——整车质量，kg；

u——纵向车速，km/h；

g——重力加速度，取9.8 m/s2；

ω——车轮旋转角速度，rad/s；

φ——路面附着系数；

R——车轮的滚动半径，m；

IW——车轮绕转轴的转动惯量，kg·m2；

Fxb——地面制动力，N；

FN——地面法向反力，N；

G——车轮重力，N；

Tb——制动力矩，N·m。

1.2 轮胎模型及制动器模型

采用双线性轮胎模型[3]44-45，用图2所示的2条直线段近似反映纵向附着系数与车轮滑移率之间的关系。纵向附着系数的计算[4]，如式（2）所示。

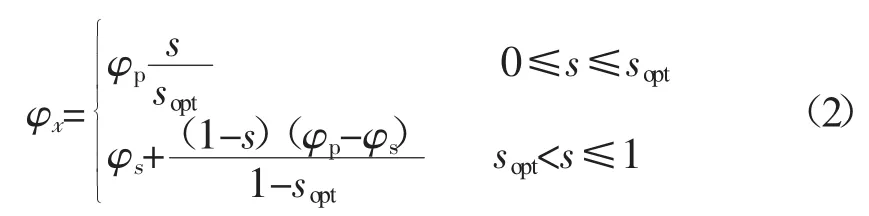
式中：φx——纵向附着系数；

s——车轮滑移率；

sopt——最佳滑移率；

φp——峰值附着系数；

φs——滑动附着系数。

图2 纵向附着系数-滑移率曲线图

制动器模型主要反映制动器制动力矩随制动轮缸压力的变化关系，建立液压制动器数学模型，如式（3）所示。

式中：Kf——制动器制动系数，N·m/kPa；

P——制动轮缸压力，kPa。

由于制动系统的机械部件之间存在间隙及摩擦，且制动液压管路中的液压油存在一定的黏度和压力损失，因而在计算轮缸制动压力时加入1阶惯性环节，其传递函数表达式为：

式中：s*——复变量；

G（s*）——1阶惯性环节传递函数；

T——时间常数。

1.3 车轮滑移率最大制动减速度制动距离的计算

s用于表征汽车制动过程中车轮相对于纯滚动状态的偏离程度[5]，其表达式，如式（5）所示。

汽车制动过程中的最大制动减速度反映地面制动力的大小，直接影响汽车的制动距离，装有ABS的汽车最大制动减速度为[1]97：

式中：abmax——汽车最大制动减速度，m/s2。

汽车的制动距离是评定其制动效能的重要指标，制动距离与汽车的行驶安全密切相关，其大小主要由初始制动纵向车速、制动器的作用时间及最大制动减速度决定。汽车制动距离的表达式为[1]99：

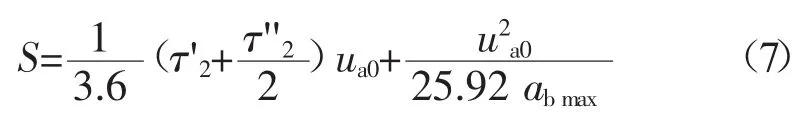
式中：S——制动距离，m；

ua0——初始制动纵向车速，km/h；

τ2'——制动器制动力相对于制动踏板力滞后时间，s；

τ2''——制动器制动力增长过程所需的时间，s。

2 ABS逻辑门限控制

2.1 ABS控制原理分析

汽车制动力系数（φb）为地面制动力与垂直载荷的比值[1]92，车轮在不同s下，其φb也会不同。φb随s的变化曲线，如图3所示。由图3可以看出，φb起初随s的增加而迅速增加，随后其缓慢增加至φp，当s进一步增加时，φb从φp下降至φs（此时s=1，车轮完全抱死）。ABS主要由轮速传感器、电子控制单元（ECU）、制动主缸、轮缸及液压调节器等部件组成。其工作原理[1]121为轮速传感器将采集到的车轮旋转信号传递给ECU，ECU对轮速信号进行处理后输出指令并传递给液压调节器，使其对制动管路的压力进行调节，保证制动过程中的sopt，即将s控制在图3所示的0.15～0.2，以防止车轮发生抱死。

图3 制动力系数-车轮滑移率曲线图

当 s位于 0.15～0.2 时，φb取值为 φp，由式（6）可知，此时abmax取最大值，且根据式（7），在ua0等条件保持不变的前提下，进而得知汽车的制动距离，此时取最小值，因而引入ABS对汽车制动过程进行控制可以有效地提高制动效能，缩短制动距离，提高汽车制动的安全性。

2.2 ABS逻辑门限控制方法及控制逻辑

基于ABS控制原理，采用ABS逻辑门限控制方法对汽车的制动过程实施控制，其基本控制思想是将s控制在0.15～0.2的最佳范围内，具体控制过程[6]如下。

1）汽车开始制动时，驾驶员踩下制动踏板，制动系统液压管路压力升高，制动器制动力也随之上升，车轮旋转角速度也相应减小，车轮开始出现滑移；

2）当s升至最佳范围的上限值（0.2）时，采用ABS控制并减小制动轮缸压力，降低制动力，使车轮转速有所上升，从而减小s；

3）当s降至最佳范围的下限值（0.15）时，采用ABS控制并增大制动轮压力，增加制动力，从而适当地降低轮速，以提高s。

基于上述控制思想，建立单轮汽车制动系统ABS控制逻辑[7]，如图4所示。

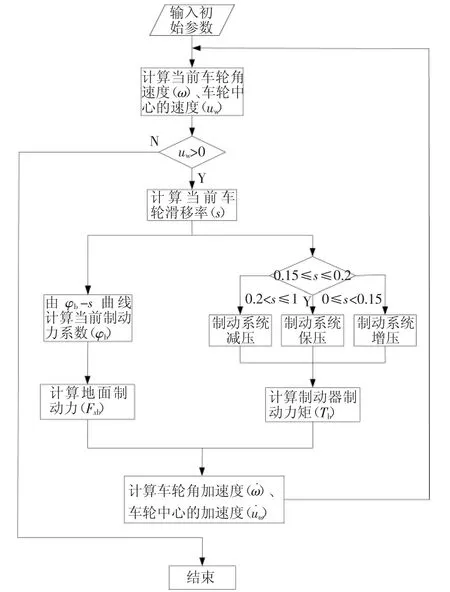
图4 单轮汽车制动系统ABS控制逻辑图

3 ABS仿真分析

采用MATLAB/Simulink搭建单轮汽车制动系统ABS逻辑门限控制仿真模型，如图5所示。仿真模型中的具体参数，如表1所示。

表1 汽车ABS仿真模型具体参数

为了验证ABS的控制效果，选取车轮sopt为0.2，设定仿真时间为15 s，采用Ctrl的不同取值表示有无ABS控制（Ctrl=1代表有ABS控制，Ctrl=0代表无ABS控制），对有无ABS控制的汽车进行对比仿真，得到仿真结果，如图6～图8所示。从图6可以看出，无ABS控制的汽车在5.13 s时车轮已发生完全抱死，而施加ABS控制后的汽车则9.97 s后车轮转速才逐渐减小为0。

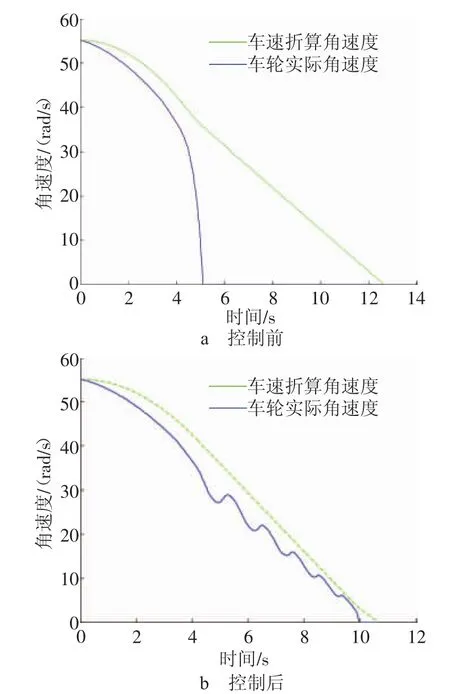
图6 ABS控制前后车轮角速度变化曲线图

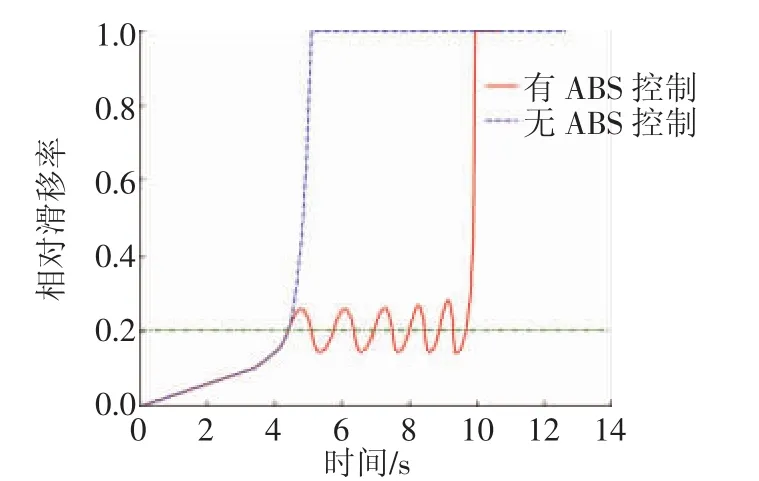
图7 ABS控制前后的车轮相对滑移率曲线图

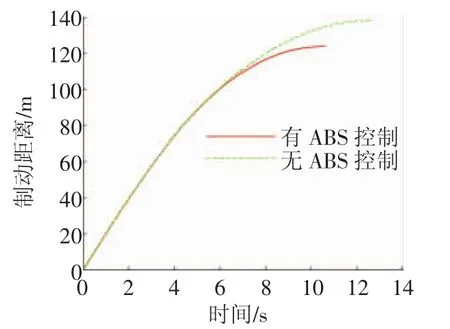
图8 ABS控制前后的汽车制动距离曲线图

结合图7，施加ABS控制前后的车轮相对滑移率在4.42 s时均达到最佳滑移率（0.2），4.42 s后，无ABS控制的车轮相对滑移率迅速增加至1，与图6a的结果保持一致，此时车轮完全抱死，而施加ABS控制后的车轮相对滑移率以最佳滑移率（0.2）为基准，并以0.05的幅度等周期上下波动，直至9.97 s时车轮相对滑移率才上升至1。从图8中可以看出，无ABS控制的汽车制动距离为138.28 m，而施加ABS控制后的汽车制动距离为123.75 m，因而施加ABS控制可以缩短汽车的制动距离。

综合上述分析可知，无ABS控制的汽车在紧急制动过程中车轮极易发生抱死，若车轮为转向轮，则该车轮失去转向能力，且汽车制动距离有所增加。施加ABS控制可以有效地防止车轮抱死，车轮不会丧失转向能力，且能够缩短汽车制动距离，提高行车的安全性。

4 结论

针对制动工况下的汽车，建立了单轮汽车系统动力学模型，采用ABS逻辑门限控制算法根据最佳和实际车轮相对滑移率的差值对制动轮缸压力进行调节，进而实现对车轮制动力的控制。结合有无ABS控制的汽车进行对比仿真，结果表明，该控制方法可以较好地将汽车滑移率控制在最佳范围，提高了汽车的制动效能，有效地缩短了制动距离，对于提高汽车的行驶安全性具有一定的作用。