提高学生有理数运算能力的措施分析

文/龙川县老隆镇维嘉学校 曾惠宇

提高学生有理数运算能力的措施分析

文/龙川县老隆镇维嘉学校 曾惠宇

运算能力是学生必须掌握一项基本数学能力，指的是根据概念、公式、法则等理解算理，并熟练应用于各个运算试题，找到适合问题条件的运算途径，正确解答问题。从中可以看出，运算能力不是单纯的数学公式、法则运用，还涉及学生对所学知识的体验、主动建构。为此，提高学生有理数运算能力可以从重视概念教学、增强符号感及运算顺序把握等方面入手。

一、重视基本概念的教学，提高学生有理数运算能力

学生在有理数运算时出错，准确率不高，很大一部分是由于对相关的基本概念理解模糊或混淆造成的。提高学生有理数运算能力，在日常教学中，就应重视基本概念的教学，为提高学生有理数运算能力打下基础。

在有理数这一章中，学到的概念都是比较重要的。特别是数轴、相反数、绝对值这三个概念的教学。数轴是表示数的工具，它的价值，更在于它是思维工具，教学中要体现“数形结合”这个重要的数学思想。能帮助学生直观地判断有理数的大小，预估有理数运算的结果作用。学生在学习有理数的四则运算及其法则时，都要涉及相反数、绝对值等基本概念。这两个概念对中学代数来说非常基本，而且是常用的概念，因而要在教学中特别下功夫。教学中要向学生讲清楚相反数、绝对值的定义及其几何意义。用数形结合的方法帮助学生理解这两个概念。在讲述定义时，应注意这两个概念都是分段定义的。让学生真正“吃透”这些概念的内涵。在进行有理数运算时，才不会模糊、混淆，从而提高运算能力。

二、加强学生符号感培养，提高学生有理数运算能力

现实中，不少学生对有理数中的符号有错误认识，特别是刚从小学升入初中的学生。小学阶段，学生认为加法就是“+”，代表着数量的增加，减法就是“-”，代表着数量的减少。但是上了初中，学习有理数时，赋予“+”“-”这两个符号新的意义，它们不但是小学里的运算符号加、减，还是性质符号正和负。

学生往往会受到多年的数学知识学习而产生的思维定势的影响。在有理数运算中，将加、减和正、负号混淆，而导致运算错误。因此，在计算中，学生要准确判断“+”“-”是运算符号还是性质符号。才能使运算的结果准确。通常情况下，两个符号连用的式子里,括号内的“+”“-”读作“正”、“负”,括号间的“+”“-”读作“加”“减”，如（-2）-（+3）+（-4）读作“负2减正3加负4”；省略加号的式子,例如“10+15-22”中的“+”“-”号既可以看成是数的性质符号,读作“10、+15、-22的和”,又可看成是运算符号,读作“18加20减42”。应培养学生养成看作是性质符号和的形式。计算过程中运算符号尽量省略，最好统一成只有性质符号。如上式（-2）-（+3）+（-4），通过应用运算律就变成“-2、-3、-4的和”。

三、通过运算顺序的把握，提高学生有理数运算能力

在一些有理数运算中，经常看到大括号、中括号、小括号和加、减、乘、除符号的混合存在，运算复杂性较大。面对此类的复杂运算，除了正确运用运算法则外，还要注意把握运算顺序。有括号的式子，先做括号里面的运算，顺序是从小到中，再到大。然后，做括号外面的运算。这部分，一般先进行第三级运算（乘方），再做第二级运算（乘、除），最后第一级运算（加、减）。遇到同级运算时，按照从左到右的顺序进行计算。同一级（都是加减，或都是乘除）运算，小学中讲，自左至右依次演算。最好改成，都是加、减时，变减去一个数为加上它的相反数，写成省略加号代数和形式，随意交换结合，选择最合适的方案。例如，消去相反数，把整数、小数、分数分别相加，分数中又把同分母或分母易通分的先加等。都是乘除法时，则变除为乘以除数的倒数，整体约分。

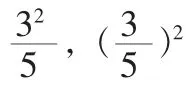
四、运算时书写要规范，养成检验的习惯

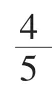
责任编辑 龙建刚