集成岸桥分派的在线泊位分配问题
2017-08-16陈光亭
杨 帆,张 安,陈 永,陈光亭
(杭州电子科技大学理学院,浙江 杭州 310018)
集成岸桥分派的在线泊位分配问题
杨 帆,张 安,陈 永,陈光亭
(杭州电子科技大学理学院,浙江 杭州 310018)
主要研究一类集成岸桥分派的在线泊位分配问题.考虑了3个连续泊位、4台岸桥的情形,以极小化集装箱货轮的总处理(装载、卸载任务)时间为目标函数,证明了最好可能的在线分派方案是2-2-0,并设计了竞争比为5/4的最优在线泊位分配算法.
岸桥分派;泊位分配;在线算法;竞争比
0 引 言
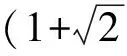
1 问题描述与基本符号
记3个连续的泊位分别为b1,b2,b3,考虑到泊位空间的限制以及岸桥的安全距离要求,一般假定每个泊位至多分派两台岸桥[4-5].因此,4台岸桥在3个连续泊位上的分派方案只可能有3种:2-2-0,2-1-1,1-2-1(依据下文货轮的类型,2-0-2分派方案相对于2-2-0分派方案属于劣势分派方案,因此不再考虑2-0-2方案).根据停靠泊位的情况,集装箱货轮也分为停靠1个泊位的小型货轮与停靠2个泊位的大型货轮两种类型.为简化模型,记小型货轮的装卸需求量为1,大型货轮的装卸需求量为Δ,且一般有Δ≥2[4-5].如果一艘大(小)型货轮停靠的泊位上共有m(m≥1)台岸桥,那么它的处理时间为Δ/m(1/m).在线问题是指货轮及其需求是实时产生的,决策者只有在需求产生后才能决定如何分配泊位.为方便起见,假设货轮的需求量按I=(r1,r2,…,rn)顺序到达,其中ri=1或Δ,目标是极小化这批需求的总处理时间.由于岸桥总数为4台,因此最少处理时间C*(I)必然满足:
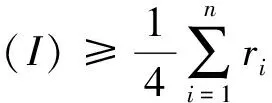
(1)
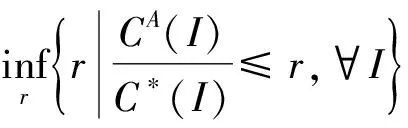
2 算法设计与竞争比分析
首先给出在3种可能的岸桥分派方案下在线泊位分配问题的下界.
定理1 当岸桥分派方案为2-2-0时,任意在线泊位分配算法的竞争比至少是5/4;当岸桥分派方案为2-1-1或1-2-1时,任意在线泊位分配算法的竞争比至少是2.
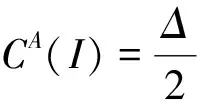
接着给出岸桥分派方案为2-2-0时的最优在线泊位分配算法.
算法H 1)若ri=Δ,则将其放在泊位b1,b2上尽可能早地完成装卸需求;
2)若ri=1,则将其按照最早完工规则分配在b1或b2上.
引理1 算法H在执行过程中至多产生一个空闲时段且其时长为1/2.
证明 显然,占用2个泊位的大货轮需求不可能产生空闲时段,小货轮产生的空闲时长必然等于其处理时间1/2.假设算法H在执行过程中产生了2个时长为1/2的空闲时段,根据算法第2步,产生第二个空闲时段的小货轮需求将被分配在第一个时长为1/2的空闲时段,因此不可能产生新的空闲时段,与算法H在执行过程中产生了2个时长为1/2的空闲时段的假设矛盾!所以结论成立.证毕.
定理2 算法H的竞争比不超过5/4且是最优的.
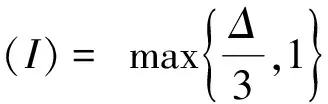
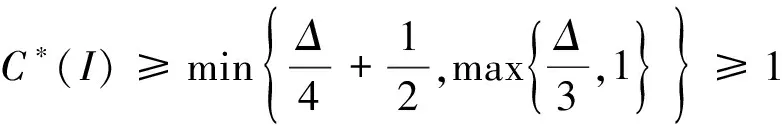
(2)
下面不妨假设最后一个货轮需求rn决定算法的目标值,对rn的取值讨论如下,最后一个货轮需求情况如图1所示.图1(a)中阴影部分表示空闲时段.
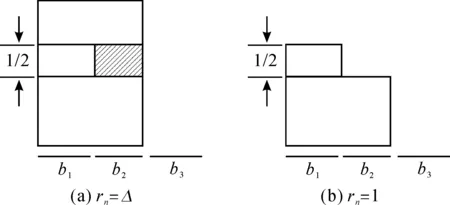
图1 最后一个货轮需求情况
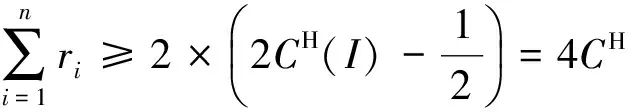
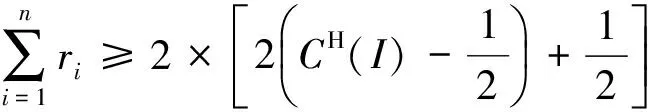
综上,算法H的竞争比不超过5/4.由定理1,算法H是最优的.证毕.
定理1和定理2的结果还表明,对应在线泊位分配的最好可能的岸桥分派方案是2-2-0.然而对离线泊位分配问题,用以下实例说明每一种岸桥分派方案都可能是最优的.
表1给出3个实例,对每一个例子分别可以得出在3种岸桥分派方案下的最优完工时间,通过比较3种岸桥分派方案的完工时间得出最优岸桥分派方案,表1中“*”对应最优方案.
3 岸桥分派方案可动态调整的讨论
上一节将岸桥分派方案的选取与泊位的在线分配分别独立考虑,本节讨论岸桥分派方案可以动态调整的情形,即在泊位分配过程中允许实时调整岸桥分派方案.对离线问题,下述实例表明岸桥方案的动态调整可以显著减少目标值.
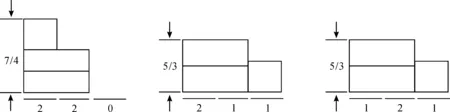
图2 岸桥分派固定方案
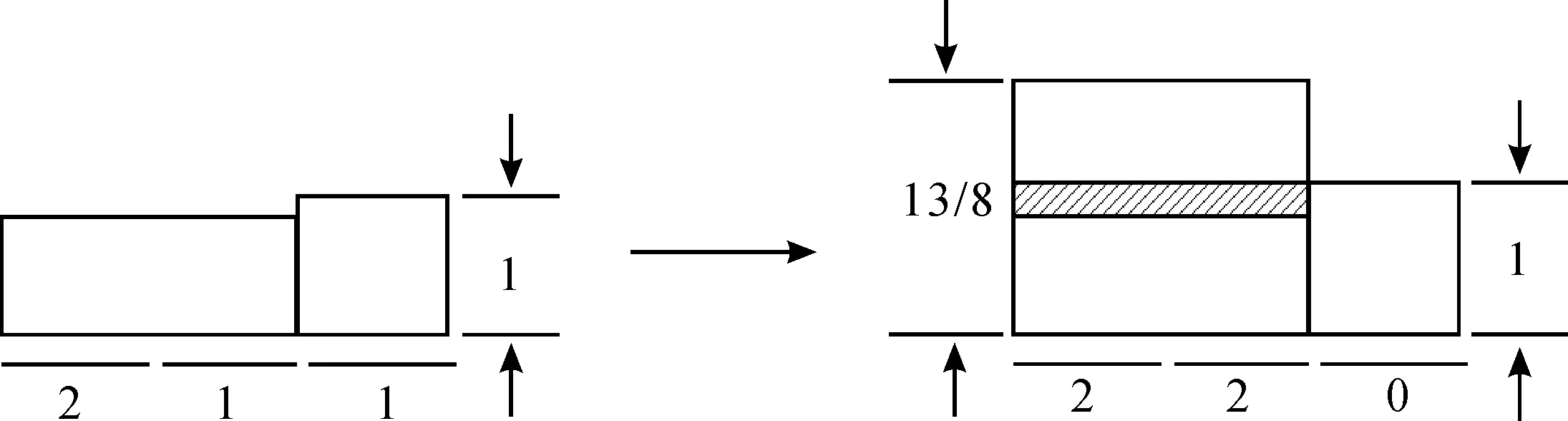
图3 岸桥分派可动态调整方案
对在线泊位分配,有以下结论表明.
定理3 如果泊位分配过程中岸桥分派方案可以动态调整,任意在线泊位分配算法的竞争比仍不小于5/4.
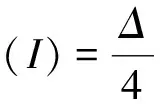
由定理3,即使允许动态调整岸桥分派方案,选取固定岸桥分派方案2-2-0的在线泊位分配算法H仍是最优的.从而表明,最好可能的岸桥方案是固定方案2-2-0.
4 结束语
本文研究了一类集成岸桥分派的在线泊位分配问题.对4台岸桥3个泊位这一问题给出了竞争比为5/4的最优在线泊位分配算法,并证明了2-2-0为最好可能的岸桥分派方案.下一步将对岸桥与泊位的数量进行进一步推广.
[1]PARK Y M, KIM K H. A scheduling method for berth and quay cranes[J]. OR spectrum, 2003,25(1):1-23.
[2]BIERWIRTH C, MEISEL F. A survey of berth allocation and quay crane scheduling problems in container terminals[J]. European Journal of Operational Research, 2010,202(3):615-627.
[3]BLAZEWICZ J, CHENG T C E, MACHOWIAK M, et al. Berth and quay crane allocation: a moldable task scheduling model[J]. Journal of the Operational Research Society, 2011,62(7):1189-1197.
[4]ZHENG F, QIAO L, LIU M. An Online Model of Berth and Quay Crane Integrated Allocation in Container Terminals[M].Houston: Springer International Publishing, 2015:721-730.
[5]PAN J, XU Y. Online Integrated Allocation of Berths and Quay Cranes in Container Terminals with 1-Lookahead[C]//International Computing and Combinatorics Conference. Springer International Publishing, 2015:402-416.
Online Berth Allocation Problem Integrating Quay Cranes Assignment
YANG Fan, ZHANG An, CHEN Yong, CHEN Guangting
(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
This paper studies an online over-list model of integrated allocation of 3 berths and 4 quay cranes in a container terminal. The objective is to minimize the maximum completion time for loading or unloading container vessels. It proves that 2-2-0 is the best possible quay cranes assignment(QCA) scheme for online berth allocation. In addition, an optimal online algorithm with competitive ratio 5/4 is provided.
quay cranes assignment; berth allocation; online algorithm; competitive ratio
10.13954/j.cnki.hdu.2017.04.019
2016-12-02
国家自然科学基金资助项目(11571252,11401149);浙江省自然科学基金资助项目(LY16A010015)
杨帆(1992-),女,河南新乡人,硕士研究生,组合优化.通信作者:陈光亭教授,E-mail:gtchen@hdu.edu.cn.
O221.7
A
1001-9146(2017)04-0086-04
