侦察模式下星载合成孔径雷达工作模式鉴别
2017-08-16夏周越
夏周越,钟 华,陈 维
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
侦察模式下星载合成孔径雷达工作模式鉴别
夏周越,钟 华,陈 维
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
星载合成孔径雷达SAR技术在侦察领域中的广泛应用推动了星载SAR干扰技术的快速发展,SAR侦察技术正是SAR干扰的关键环节.在星载SAR常用工作模式的基础上,基于SAR信号地基侦察模型,进行了信号侦察与模式鉴别的研究.从截获的星载SAR信号入手,提出了基于分数阶傅立叶变换与最小熵估计的处理算法,通过有效估计得到星载SAR的方位向接收功率图,从而鉴别星载SAR的工作模式.仿真实验验证了算法的有效性与可靠性.
雷达侦察;工作模式;分数阶傅立叶变换;最小熵估计
0 引 言
星载合成孔径雷达(Synthetic Aperture Radar, SAR)作为一种全天候、全天时的主动成像雷达,具有远程、宽幅、高分辨等优点.此外,波长较长的SAR信号还可以穿透覆盖物,对隐藏在地表伪装物以下的目标进行成像[1].因此,星载SAR技术在区域侦察、活动监测、目标识别等领域得到了广泛应用[2-3].针对这种状况,必须积极发展星载SAR的干扰对抗技术,以破坏和削弱对方星载SAR的性能优势.当前,在SAR侦察方面,研究人员已经进行了若干探索性研究.例如,文献[3]介绍了利用截获信号信息对星载SAR的干扰方法,但其对星载SAR的工作模式信息主要是利用SAR卫星的轨道信息来预测的.文献[4]利用SAR卫星天线及轨道参数,建立了星载SAR地基侦察信号的侦察模型.文献[5-6]根据该星载SAR地基侦察模型,研究了不同工作模式下SAR信号的截获难易程度和接收功率的形态,但并未对SAR信号的截获、估计与模式判决方法进行深入的研究.
本文在接收功率形态分析结果的基础上,基于分数阶傅里叶变换(Fractional Fourier Transform,FrFT)与最小熵估计法提出了一种对回波数据的接收功率形态和多普勒参数进行估计的星载SAR工作模式鉴别方法,并在星载SAR地基侦察机的背景下,利用TerraSAR-X的工作参数和轨道参数进行了仿真验证.
1 工作模式与接收功率
1.1 常见的工作模式
随着SAR技术的发展,星载SAR已经具备了多模式成像的工作能力.星载SAR常见工作模式分为条带模式、聚束模式和滑动聚束模式.条带模式是星载SAR最常用的工作模式,波束随卫星平动在观测区域呈现条带状测绘带.聚束式可以获得比条带式更大的合成孔径长度,从而获得更高的方位分辨率.滑动聚束式可以获得比条带式更高的分辨率,比聚束式更大的测绘区域,从而在高分辨率和大面积成像中得到很好的权衡.3种工作模式的侦察模型如图1所示.图1中,t为方位慢时间,t0为起始时刻,θ为侦察机偏离主瓣的夹角,θs为斜视角,R(t)为侦察机到卫星的斜距,v为卫星等效飞行速度.
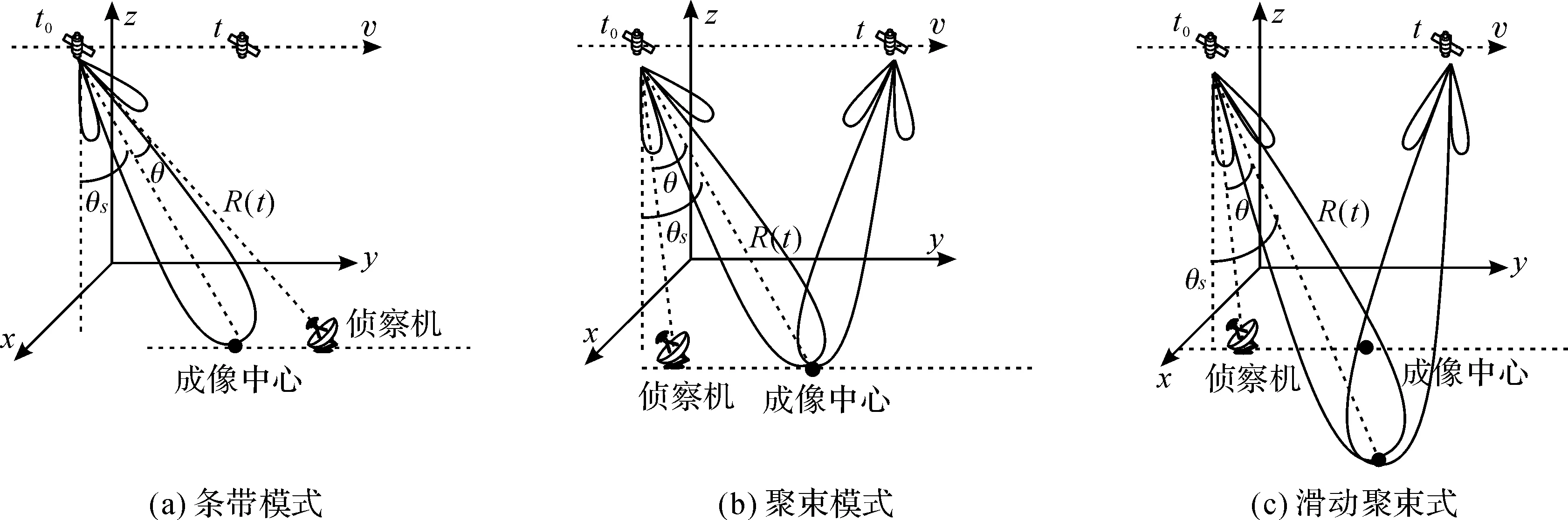
图1 星载SAR常见工作模式的侦察模型
1.2 接收功率
设SAR卫星的发射天线功率为Pt,天线增益为Gt(θ),它与偏离主瓣的夹角成正比[6],即:
(1)
其中,Da为天线方位向尺寸,λ为波长.信号经馈线从接收天线到接收机会产生损耗,设损耗率为φ(φ≤0.5).由于侦察天线的极化方向与SAR的极化方向不同,只能接收信号功率的一半.因此,取极化系数η=0.5.
在地基侦察机处星载SAR信号的功率密度Sr为:
(2)
信号经馈线到侦察机输入端的功率为Pr为:
(3)
其中,A为接收天线等效面积,α=0.5,φ=0.5,η=0.5.
2 基本原理
地基侦察机截获到的星载SAR信号是一个未聚焦的周期性脉冲串,假设对接收信号进行了接收功率方向图补偿和距离衰减功率补偿,那么接收信号可表示为
(4)
其中,τ为距离向快时间,t为方位向慢时间,wrg()和waz()分别为距离向和方位向包络函数,K为调频斜率,R(t)为瞬时距离,c为光速,Δf为频差,λ为波长.
由式(4)可见,方位向接收功率形态就是由包络函数waz()决定的.由于waz()和多普勒调制函数exp{j2πR(t)/λ}分布在距离延迟曲线R(t)/c上,而星载SAR的方位向积累时间较长,距离延迟曲线横跨了数十到数百个距离分辨单元,必须进行距离徙动矫正,才能对方位向天线方向图进行有效估计.因此在脉冲压缩之前需进行距离向参数估计,以获取距离匹配滤波参数.
2.1 距离压缩
对星载SAR信号进行距离压缩,必须获取chirp信号的调频斜率.在常规雷达的信号处理中,估计线性调频信号的参数一般采用时域估计和短时傅里叶变换的方法.而在SAR侦察中对工作频率和调频斜率等细微特征参数的估计精度要求较高,可以采用FrFT的方法.
检测星载SAR的距离向信号的基本思想就是以旋转角度α为变量进行扫描,求距离信号的FrFT,从而形成信号能量在参数{α,u}平面上的二维分布,在此平面上按阈值进行峰值点的二维搜索即:
(5)
星载SAR距离向信号的调频率K和频差Δf与参数{α,u}的关系为:
(6)
然后利用估计出来的距离向信号的调频率K进行距离压缩,处理后得到距离向聚焦的星载SAR信号,再进行距离走动矫正.
2.2 自适应距离走动矫正
距离徙动可以分解为距离走动和距离弯曲两部分,而在星载条件下距离走动绝对占优.基于上述结论,本文采用基于最小熵的自适应线性距离走动矫正法.从SAR成像处理研究可知,接收信号是对比度绝对占优的点辐射源信号,该方法可以取得较好的估计和矫正效果[8].
无论处于何种成像模式下,侦察机到卫星的瞬时斜距R(t)都是相同的,可表示为:
(7)
由式(7)可见,距离走动单元可表示为:
ΔR(t)=Kt=-vsin(θs)t
(8)
进行距离走动矫正的相位乘法器为:
(9)
距离走动斜率初始值K0=-vsin(θs),ΔK为迭代步长,以K=K0+ΔK对信号进行距离走动矫正,在方位向对经距离走动矫正后的数据进行积分得到E,然后计算整个迭代过程中距离走动矫正后的信号的熵:
(10)
其中,N为距离向采样点数.最小熵Hemin对应的距离走动斜率K即为所求的距离走动斜率.基于最小熵的单点目标距离走动矫正仿真结果如图2所示.
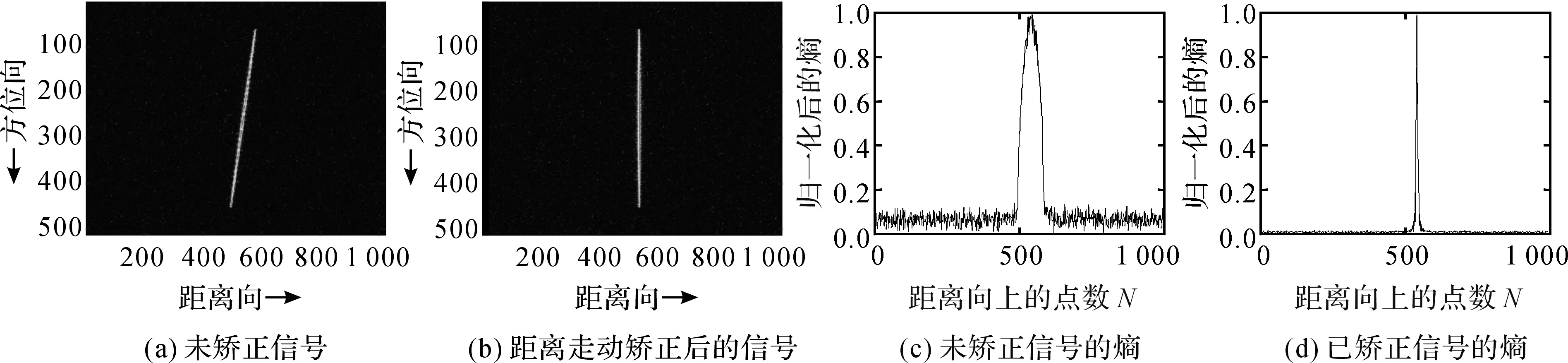
图2 基于最小熵的单点目标距离走动矫正
2.3 工作模式判决
经距离匹配滤波和自适应距离走动矫正后的星载SAR信号,其信噪比得到了提高.然后从距离延迟曲线中估计出方位向接收功率,得到方位向功率图.条带模式下的功率变换速度最快,聚束模式下的功率变换最小,滑动聚束模式介于两者之间.方位接收功率形态只能定性判决3种工作模式,为了使本方法更加有效,利用Radon变换估计不同工作模式的多普勒参数并重建多普勒历程[9].利用多普勒频率的变化范围和多普勒调频率来辅助判决工作模式.
3 仿真计算
3.1 接收功率估计的仿真
基于FrFT和最小熵的接收功率估计仿真参数如表1所示,在仿真中加入了与信号等幅度的高斯白噪声.

表1 仿真参数
接收功率估计的仿真结果如图3所示,其中接收功率是归一化的接收功率.
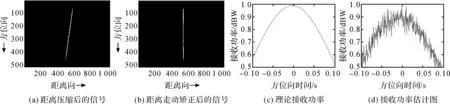
图3 基于最小熵接收功率估计的仿真结果图
3.2 3种工作模式的仿真
利用STK卫星工具箱对星载SAR常见的3种工作模式建立侦察模型,生成3种工作模式下星载SAR的发射信号(时长20 s).仿真中发射信号加入了与信号等幅度的高斯白噪声,仿真采用的卫星轨道参数为TerraSAR-X卫星的轨道参数,如表2所示.

表2 TerraSAR-X卫星轨道参数
地基侦察机截获到星载SAR信号后,利用FrFT与最小熵的算法进行距离压缩和距离走动矫正,估计出3种工作模式下的方位向接收功率如图4所示.
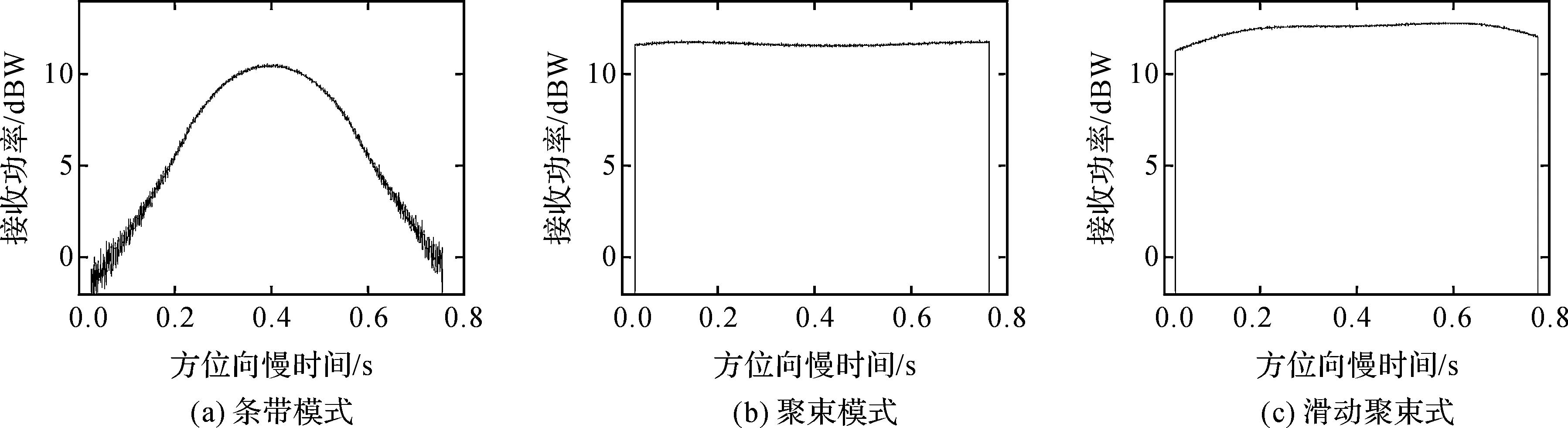
图4 3种工作模式的方位向接收功率图
为了定量分析3种工作模式的多普勒差异,根据文献[9]的方法对3种工作模式的侦察信号进行多普勒参数估计.由于STK卫星工具箱生成的数据时长为20 s,分别取2 s~3 s,8 s~9 s和11 s~12 s的数据段进行估计.参数估计的结果如表3所示.

表3 3种工作模式的多普勒参数估计结果
利用表3的数据重建3种工作模式的多普勒历程.首先,比较条带模式与聚束模式,从表3可知,这2种模式的调频率均值分别为-4 516.85 Hz/s和-4 798.91 Hz/s,聚束式模式明显占优.其次,比较条带模式和滑动聚束模式,滑动聚束模式有一个显著特点可以被观测到,即由于其波束沿着虚拟中心转动,接收功率的变化没有条带模式明显,因此再结合图4的接收功率形态可以判断出条带模式和滑动聚束模式.
仿真实验结果表明,接收功率形态和多普勒历程两者可以综合判决3种工作模式.
4 结束语
本文在侦察模式下,对星载SAR的工作模式进行了研究和鉴别.在截获的星载SAR信号基础上,提出了一种利用分数阶傅里叶变换与最小熵的方位向功率估计算法,并综合利用参数估计的结果对星载SAR进行工作模式的鉴别.仿真实验结果证明了本文所提的模式判决方法的可靠性和功估计方法的有效性,为后期的SAR干扰对抗系统的研究提供了一定的信息保障.在本文的研究基础上可以进一步提高估计算法的速度,而且可以利用更多的特征辅助鉴别工作模式,这也是下一步研究的方向和重点.
[1]邓云凯,赵凤军,王宇.星载SAR技术的发展趋势及应用浅析[J].雷达学报,2012,1(1):1-10.
[2]刘寒艳,宋红军,程增菊.条带模式、聚束模式和滑动聚束模式的比较[J].中国科学院研究生院学报,2011,28(3):410-417.
[3]INGLADA J, VINCENT A, ARIAS M, et al. Improved Early Crop Type Identification By Joint Use of High Temporal Resolution SAR And Optical Image Time Series[J]. Remote Sensing, 2016,8(5):362.
[4]叶伟,刘鑫,高阳.星载SAR地基侦察信号建模与仿真[J].舰船电子对抗,2012,35(5):61-65.
[5]陈颖颖,贾鑫,吴彦鸿.对聚束和滑动聚束模式下星载合成孔径雷达的旁瓣侦察比较研究[J].科学技术与工程,2012,20(8):1785-1789.
[6]陈颖颖,吴彦鸿,贾鑫.对不同工作模式星载合成孔径雷达的侦察研究[J].计算机工程与应用,2013,49(12):223-227.
[7]LI W, YANG J, HUANG Y, et al. A geometry-based Doppler centroid estimator for bistatic forward-looking SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2012,9(3):388-392.
[8]钟华,宋广华,杜昌平.一种双站合成孔径雷达的高分辨率成像与合成方法[J].上海交通大学学报,2014,48(3):317-322.
[9]钟华,陈维,杨萌.侦察模式下星载SAR多普勒参数估计[J].杭州电子科技大学学报,2016,36(5):17-21.
Identification of the Spaceborne SAR Operating Modes under Reconnaissance Mode
XIA Zhouyue, ZHONG Hua, CHEN Wei
(SchoolofCommunicationEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Spaceborne synthetic aperture radar(SAR) technology has been widely used in the field of reconnaissance, which has promoted the rapid development of the spaceborne SAR jamming technology, and the SAR reconnaissance technology is the key of SAR interference. In this paper, on the basis of the common operating mode of SAR, the signal detection and pattern identification are carried out based on the SAR signal ground detection model. From intercepted spaceborne SAR signal, this paper introduces the processing algorithm based on fractional Fourier transform and the minimum entropy to estimate the effective estimation of the Spaceborne SAR power, and to identify the operation mode of SAR. The simulation results verify the validity and reliability of the algorithm.
radar reconnaissance; operation mode; fractional Fourier transforms; minimum entropy
10.13954/j.cnki.hdu.2017.04.008
2016-12-21
夏周越(1994-),男,浙江湖州人,本科生,信号与信息处理.通信作者:钟华讲师,E-mail:hzhong@hdu.edu.cn.
TN958.4
A
1001-9146(2017)04-0036-05
