区间线性不等式系统的代数解
2017-08-16胡金燕汤立龙
胡金燕,李 炜,汤立龙
(杭州电子科技大学运筹与控制研究所,浙江 杭州 310018)
区间线性不等式系统的代数解
胡金燕,李 炜,汤立龙
(杭州电子科技大学运筹与控制研究所,浙江 杭州 310018)
区间优化中,各种解集及其特征是区间分析与区间优化领域的一个重要的研究课题.通过对实矩阵与区间向量乘积的中点—半径的刻画,在已有结论的基础上,给出了求解区间线性不等式组代数解的方法.最后,通过识别函数给出区间线性不等式组代数解的一个充要条件.
区间线性不等式组;代数解;识别函数
0 引 言
近年来,许多学者对区间线性系统的各种解集进行了深入的研究[1-3].文献[4-5]研究了区间线性方程组的代数解以及其特征,文献[6-7]定义了区间线性方程组的识别函数,利用识别函数给出了区间线性方程组有区间解的充要条件及相关性质.然而,区间线性不等式组的代数解及其特征还没有得到研究.根据文献[8],本文针对区间线性不等式组的代数解进行了讨论,给出了求解区间线性不等式组代数解的等价条件,从而得到判断区间线性不等式组有无代数解的一个充要条件.
1 代数解
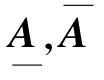
全体m×n维区间矩阵的集合记为IRm×n,n维区间向量的集合记为IRn.
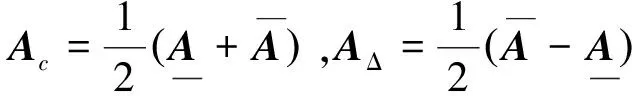
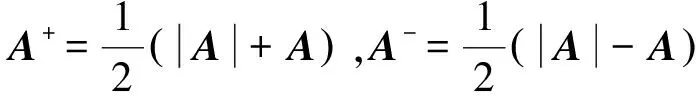
Oliver B.等[5]提出了利用区间上下界来刻画AxI的形式,但未给出证明.本文中,为了应用方便,利用中点—半径形式来刻画AxI,进而推出中点—半径形式等价于文献[5]中所刻画的上下界形式.
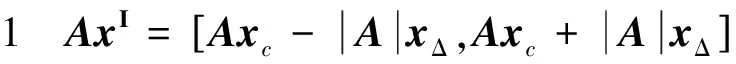
证明 设A∈Rm×n,xI∈IRn,记
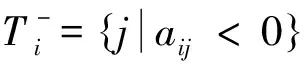
由于
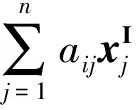
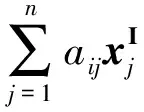
而
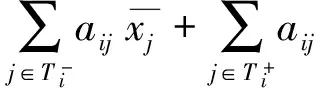
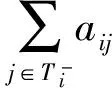
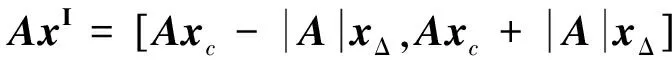
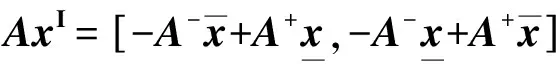
证明 由区间向量中点和半径的定义易知
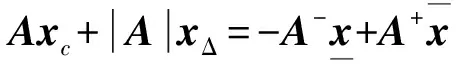
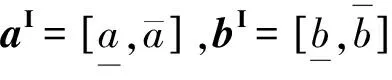
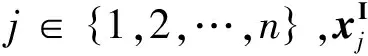
由定义1以及引理1得:
定理1 设A∈Rm×n,xI∈IRn,bI∈IRm,从而AxI≤bI等价于
(1)
例 求AxI≤bI的代数解,其中
在信息技术支持下进行小学数学问题导向式和谐课堂教学,其内容的基本依据依然是现有教材。教材是教育部门根据学生学习基本情况拟定的相对科学的和谐课堂教学书籍,教师在进行和谐课堂教学活动前,应先制定和谐课堂教学计划,将教学的主要内容筛选出来,并针对性地制作与信息技术、设备相匹配的和谐课堂教学课件、道具等。

解 由式(1)求得
故最后计算出代数解为
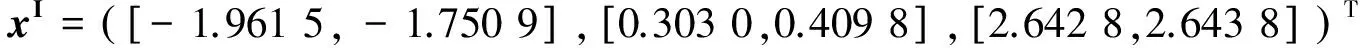
2 识别函数
Sergey P.S.[6]利用Oettli-Prager不等式推导出了刻画区间线性方程组弱解特性的识别函数,下面给出区间线性不等式组代数解的识别函数.
定义3 设区间向量xI∈IRn,矩阵A∈Rm×n,区间向量bI∈IRm.称函数Uss∶IRn×Rm×n×IRm→R为区间线性不等式系统AxI≤bI代数解的识别函数

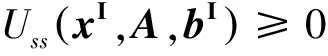
证明 首先证明必要性.设xI∈IRn,由于xI是AxI≤bI的代数解,因此可知xΔ≥0.由引理1可知
因此在xΔ≥0下,由定理1知AxI≤bI等价于
(2)
(3)
有
(4)
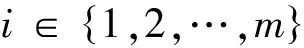
(5)
因此,
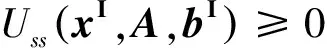
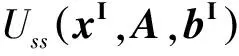
即
因此根据式(2)、式(3)和式(4)可证得
AxI≤bI
故由代数解的定义可知xI∈IRn是AxI≤bI的代数解.证毕.
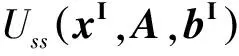
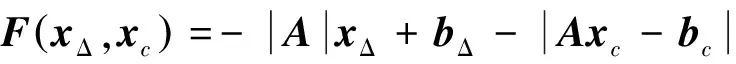
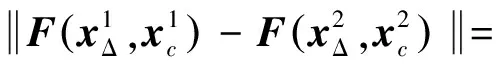
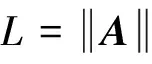
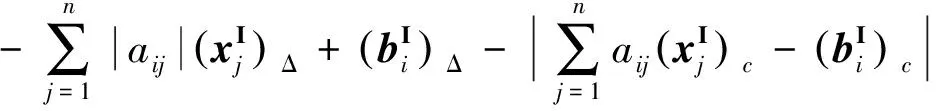
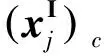
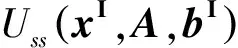
有了识别函数和它的性质,可以利用识别函数的性质来检验区间线性系统的可解性,也可以利用识别函数的性质来研究区间线性系统的相关性质.
3 结束语
本文讨论了区间线性不等式组的代数解,给出了求解方法,定义了识别函数,并利用识别函数给出了如何判断一个区间向量是区间线性不等式组代数解的一个充要条件.本文只研究了AxI≤bI的代数解,而更为一般的区间系统即AxI+ByI=bI,CxI+DyI≤dI,xI≥0I的代数解的特征是一个值得继续深入研究的内容.
[1]LI W, WANG H, WANG Q. Localized solutions to interval linear equations[J]. Journal of Computational & Applied Mathematics, 2013,238(1):29-38.
[2]LI W, LIU X, LI H. Generalized solutions to interval linear programmes and related necessary and sufficient optimality conditions[J]. Optimization Methods & Software, 2014,30(3):1-15.
[3]LI W, LIU P, LI H. Checking weak optimality of the solution to interval linear program in the general form[J]. Optimization Letters, 2016,10(1):1-12.
[4]ALLAHVIRANLOO T, GHANBARI M. A new approach to obtain algebraic solution of interval linear systems[J]. Soft Computing, 2012,16(1):121-133.
[5]BEAUMONT O, PHILIPPE B. Linear Interval Tolerance Problem and Linear Programming Techniques[J]. Reliable Computing, 2001,7(6):433-447.
[6]SHARY S P, SHARAYA I A. On solvability recognition for interval linear systems of equations[J]. Optimization Letters, 2016,10(2):247-260.
[7]SHARY S P. New characterizations for the solution set to interval linear systems of equations[J]. Applied Mathematics & Computation, 2015,265:570-573.
[8]GUERRA M L, STEFANINI L. A comparison index for interval ordering based on generalized Hukuhara difference[J]. Soft Computing, 2012,16(11):1931-1943.
Algebraic Solutions to Interval Linear Inequality Systems
HU Jinyan, LI Wei, TANG Lilong
(InstituteofOperationsandControl,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Interval optimization’s solutions set and its characterizations are important research topic in the field of interval analysis and interval optimization. In this paper, by means of the description of the midpoint-radius characterization of real matrix and interval vector product, which methods for solving algebraic solution of interval linear inequalities is given on the basis of existing results. Finally, it gives a necessary and sufficient condition for the algebraic solution of interval linear inequalities by recognizing functional.
interval linear inequality; algebraic solution; recognizing functional
10.13954/j.cnki.hdu.2017.04.017
2016-08-04
国家自然科学基金资助项目(61673145,U1509217);浙江省自然科学基金资助项目(LY14A010028);浙江省大学生科技创新活动计划(新苗计划)资助项目(2016R407079)
胡金燕(1990-),女,安徽淮南人,硕士研究生,数学规划.通信作者:李炜教授,E-mail:weili@hdu.edu.cn.
O221
A
1001-9146(2017)04-0079-04
