Vossloh300型扣件胶垫刚度频变特性对高铁高频振动的影响

豆银玲，杨麒陆，王平

（1. 高速铁路线路工程教育部重点实验室，四川 成都 610031；2. 西南交通大学 土木工程学院，四川 成都 610031）

Vossloh300型扣件胶垫刚度频变特性对高铁高频振动的影响

豆银玲1，2，杨麒陆1，2，王平1，2

（1. 高速铁路线路工程教育部重点实验室，四川 成都 610031；2. 西南交通大学 土木工程学院，四川 成都 610031）

以Vossloh300型扣件胶垫为研究对象，利用配备温度箱的万能试验机得到其在20 ℃下的静刚度值。基于Timoshenko梁理论建立车辆-轨道垂向耦合系统随机振动分析模型，探究该型扣件胶垫频变刚度在不同频段内对轮轨系统随机振动频域特征的影响规律。实验结果为：Vossloh300型扣件胶垫静刚度在3～5 Hz激振条件下的测试值为22.4 kN/mm。仿真分析表明：Vossloh300型扣件胶垫刚度频变特性对CRH380型高速动车组轮轨系统高频振动影响较小，但对其1/3倍频中心频率为40～100 Hz影响较大，扣件力最大增幅达30.98%，并且使轨道结构振动增加2 dB。因此，在进行轮轨系统振动分析时，应考虑扣件胶垫刚度的频变特性。

轮轨系统；频变刚度；Vossloh300型扣件胶垫；高频振动；Timoshenko梁模型；轨道不平顺

0 引言

近年来，我国高速铁路得到快速发展，列车运行速度大幅提高后，外界激扰频率急剧增加，使得车辆和轨道系统出现了频率超过500 Hz及以上的高频振动。中低速条件下，列车系统一般不会出现高频振动甚至结构振动，能够保持列车运行安全性、乘坐舒适性。然而，运营速度大幅提高后，会使轮轨作用加剧、车体出现不同程度颤振，加速部件疲劳断裂等现象，严重影响列车运行安全性[1]。

为保证列车运行安全，改善运行产生的噪声污染，常在轨道扣件系统内设置缓冲胶垫，其材质主要包括氯丁橡胶、天然橡胶以及聚氨脂塑料垫板等，这些材料的动刚度依赖于加载频率、加载幅值以及环境温度等[2-4]。由于试验条件限制，在以往的环境振动预测计算中，扣件胶垫动刚度仅按3～5 Hz激振条件下实测取值[5]。然而，实测数据显示：由于高铁线路等级较高，其轨道不平顺多为短波波磨，由此轮轨间的振动主要集中在高频部分。因此，在高铁环境振动分析中，将扣件胶垫刚度视为定值并不合理。为掌握扣件胶垫刚度的频变规律，确定扣件胶垫频变刚度的合理取值，我国学者近年来已开始关注扣件胶垫刚度的频变特征，并设计了一系列试验[6]，但试验的激振频率均低于10 Hz，尚无法在更高的频域范围揭示扣件胶垫刚度的频变规律。在国外，MAES等[7]设计了1∶40的聚苯乙烯橡胶改性塑料、树脂橡胶等材质的胶垫刚度频变试验（该试验的最大激振频率为2 500 Hz）。由此可见，扣件胶垫动刚度的试验研究已取得初步进展，但扣件胶垫刚度的频变现象在轮轨系统频域振动分析中的应用研究还比较滞后，尤其在高铁领域亟需开展相关研究。

Vossloh300型扣件系统已在京津城际铁路、武广高铁等线路得到广泛应用。为说明轨道系统内扣件胶垫刚度的频变特征在轮轨系统频域振动响应预测中的重要性，建立基于Timoshenko梁模型的车辆-轨道垂向耦合系统随机振动分析模型[1,8-9]。以Vossloh300型扣件胶垫为研究对象，采用实测的短波不平顺，重点研究扣件胶垫刚度随频率变化对高铁高频振动频域响应的影响规律，并揭示扣件胶垫刚度频变特性与其周边环境振动频域分布特征的内在联系。

1 刚度试验

Vossloh300型扣件是我国从福斯罗公司引进的带铁垫板的不分开式扣件。试验采用配备温度箱的万能试验机，根据规范测试Vossloh300型扣件胶垫在20 ℃下的荷载-位移曲线，并计算其静刚度值[9]。

1.1 试验装置

试验采用由上海华龙测试仪器股份有限公司生产的电液伺候万能试验机，量程为120 kN，加载精度为0.5 kN。配套温度箱由成都易华天宇试验设备有限责任公司定制生产，其量程为-70～120 ℃，精度为1 ℃。配备温度箱的万能试验机见图1。

图1 配备温度箱的万能试验机

为保证扣件胶垫在加载过程中受力均匀，在扣件上方安放铁垫板，扣件下方安放刚性支承垫板（见图2），测试用的Vossloh300型扣件胶垫见图3。

1.2 试验过程及结果

图2 Vossloh300型扣件胶垫安装

图3 Vossloh300型扣件胶垫

将温度箱内的温度设置到20 ℃，静置2 h后，以1 kN/s的加载速度对扣件胶垫进行2次预加载，预加荷载为100 kN[8]。

预加载完成后，对试验机的位移及荷载进行调零，再以1 kN/s的加载速度进行正式加载（0～100 kN），加载至F1（20 kN）和F2（70 kN）时各停留1 min，并分别记录加载钢板的位移D1、D2。

扣件胶垫静刚度计算公式为[8]：

为减小试验误差，重复进行3次加载试验，分别计算出静刚度KSTAi。取3次加载试验得到的静刚度的平均值KSTA作为该环境温度下扣件胶垫的静刚度值。

1.3 试验结果

20 ℃下扣件胶垫的荷载-位移曲线见图4，扣件胶垫静刚度实测值与平均值见表1。

图4 荷载-位移曲线

表1 静刚度实测值与平均值 kN/mm

所以，Vossloh300型扣件胶垫静刚度为22.40 kN/mm。

2 刚度频变特性对高铁高频振动的影响

基于翟婉明院士书中的车辆-轨道耦合动力学模型[8]并参考相关资料[1,10-13]，建立基于Timoshenko梁模型的车辆-轨道垂向耦合系统随机振动分析模型，并分别计算分析当行车速度增大和扣件胶垫刚度随频率变化对高铁频域随机振动响应特征的影响规律。

2.1 分析模型

2.1.1 车辆

以我国广泛采用的CRH380型高速动车组为原型建立车辆模型，该车型主要参数见表2。车体质量和点头转动惯量分别为Mc和 Jc；转向架质量和点头转动惯量分别为Mt和 Jt；车体与转向架之间通过二系悬挂连接，其刚度与阻尼分别为Ks与Cs；轮对质量为Mw，轮对与转向架之间通过一系悬挂连接，其刚度与阻尼分别为Kp与Cp。

2.1.2 轨道

高铁轨道结构为短枕埋入式整体道床。该轨道系统由钢轨、扣件（包括轨下胶垫与铁垫板等）、穿孔混凝土枕、混凝土无砟道床等组成。由于轨枕与道床板完全联结，且轨下基础质量较大，因此短枕埋入式无砟轨道的振动主要体现为钢轨的振动，可将钢轨近似视为离散点支承的Timoshenko梁，该动力学模型已较成熟，其振动微分方程见文献[14]、文献[15]。轨道结构模型参数见表3。

表2 CRH380型高速动车组主要参数

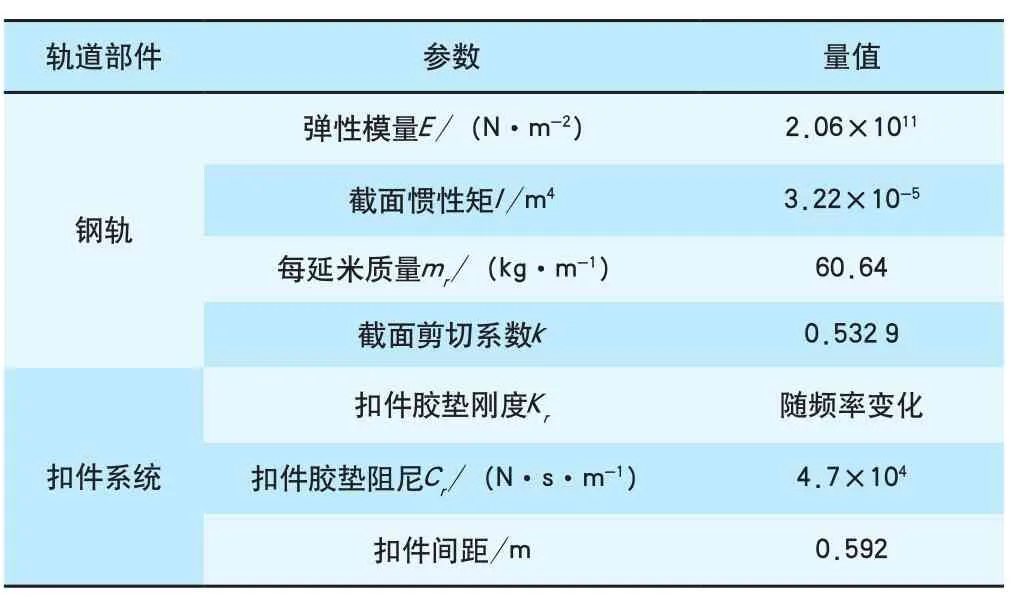
表3 轨道模型参数

Vossloh300型扣件胶垫常量刚度按扣件胶垫静刚度乘以动静刚度比取值，动静刚度比取1.4[8]。根据文献[6]可知，尽管各类橡胶材质胶垫初始刚度不同，但其刚度与激振频率在对数坐标系内近似呈线性关系[16-19]，且不同材料的线性变化斜率基本一致，该变化率的拟合公式为：

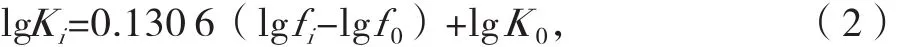
式中：f0为4 Hz；K0为4 Hz激振条件下胶垫的动刚度，取31.3 kN/mm；fi为胶垫的第i个激振频率；Ki为胶垫在激振频率 fi作用下的动刚度。

轨道谱方面，0.02～0.30 m短波部分采用某线实测轨道不平顺；2.00～200.00 m波长采用我国高速铁路无砟轨道不平顺；0.30～2.00 m波长采用在对数坐标系下线性延长我国高速铁路无砟轨道不平顺谱至0.30 m（使用2.00～6.50 m波长斜率）。经过整合，得到计算使用的高速铁路无砟轨道波长0.02～200.00 m的高低不平顺功率密度谱[19]（见图5）。

2.2 行车速度对轮轨系统随机振动的影响

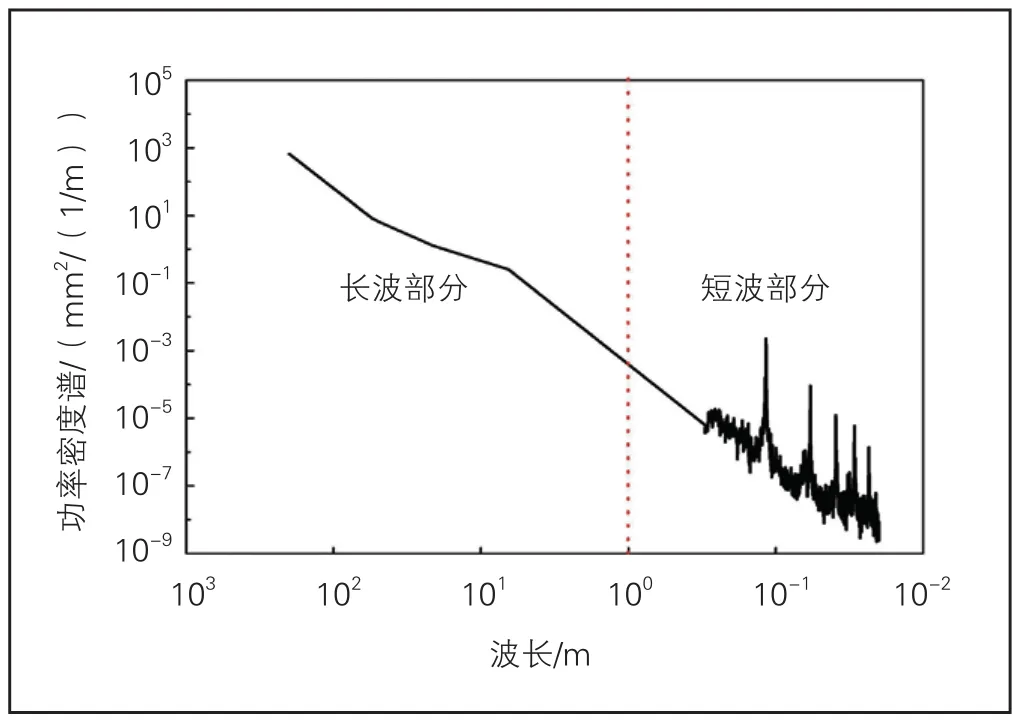
图5 无砟轨道高低不平顺功率密度谱

CRH380型高速动车组设计最高速度为380 km/h，为研究超高速行车对车辆-轨道耦合系统随机振动响应的影响，仿真模拟时行车速度分别取250、300、350和380 km/h。模型采用2节编组，以考虑相邻转向架间的相互影响。

由于轮轨系统各结构随着速度的增大变化规律一致，且轮轨噪声是铁路噪声污染的重要部分，故选取第1节车第4轮对处的轮轨力进行分析，对其功率密度谱进行1/3倍频处理得到其1/3倍频幅值谱。速度由250 km/h增加到380 km/h时，轮轨力功率密度谱和1/3倍频幅值谱见图6。

由图6（a）可知，当列车速度从250 km/h增加到380 km/h时：在中高频部分，次主频由34.5 Hz增加到54.0 Hz，增加19.5 Hz；在高频部分，轮轨力的第一主频由600 Hz增加到907 Hz，增加了307 Hz。由图6（b）可知，其第一主频幅值由6.84 kN增加到9.93 kN，增加45.2%，次主频增幅为53.8%。

由此可见，列车速度的提高对轮轨系统高频（907 Hz附近）的振动和受力影响显著，轮轨系统的第一主频和次主频（30～60 Hz）以及所对应的幅值都显著增大。

2.3 频变特性对高铁高频振动响应的影响

为探讨扣件胶垫刚度的频变特性对高铁轨道系统频域响应的影响规律，并揭示扣件胶垫刚度的频变性与其周边环境振动频域分布特征的内在联系，以图5整合的轨道高低不平顺为激励，行车速度取350 km/h。由于考虑扣件胶垫刚度频变前后车体、转向架与轮对变化规律一致，给出钢轨和轮对垂向未计权的1/3倍频加速度级（见图7）以及轮轨力和扣件力1/3倍频幅值谱（见图8）。

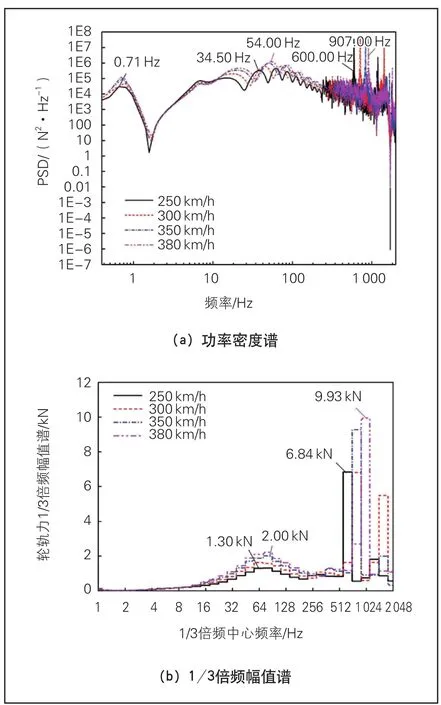
图6 不同速度下的轮轨力

由图7可知，扣件胶垫刚度频变特性对轮轨系统振动加速度影响较小。具体来说，对于轮对频率小于40 Hz或大于100 Hz，扣件胶垫刚度对轮对振动加速度级没有影响；在40～100 Hz时，轮对振动加速度级增大，最大增加量为2.1 dB。对于钢轨，考虑扣件胶垫刚度频变在1～2 Hz与60～110 Hz时，其加速度级增大，而在8～35 Hz时，其加速度级减小，最大改变量均为2 dB。

由此可知，扣件胶垫刚度频变特性主要影响轮轨系统振动加速度级中心频率40～100 Hz部分，在进行轮轨系统振动噪声分析时应考虑扣件胶垫刚度频变特性。

图7 垂向未计权的1/3倍频加速度级

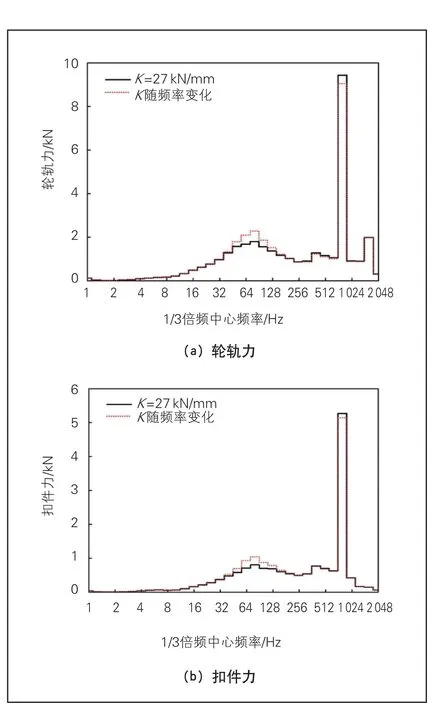
图8 1/3倍频幅值谱

由图8可知，对于轮轨力，频率在40～100 Hz时，考虑扣件胶垫刚度频变特性后轮轨力最大增幅为25.2%；在710～900 Hz时，考虑扣件胶垫刚度频变特性后轮轨力幅值降低了4.1%。对于扣件力，在40～100 Hz时，扣件胶垫刚度的频变使扣件力增大，最大增幅为30.98%；在710～900 Hz时，扣件力反而降低了2.3%。

由此可知，扣件胶垫刚度频变特性主要使轮轨力和扣件力在40～100 Hz时幅值增大，使得传递到路基的振动增大。不考虑扣件胶垫刚度的频变性将会低估轨道系统40～100 Hz的中高频振动，同时会高估710～900 Hz的高频振动。

3 结论与建议

运用Timoshenko梁模型与随机振动虚拟激励法，建立了基于Timoshenko梁模型的车辆-轨道垂向耦合系统随机振动分析模型，并讨论了扣件胶垫刚度频变特性对车体、转向架、轮对与钢轨垂向随机振动加速度频域响应的影响。所得结论与建议如下：

（1）当列车速度从250 km/h增加到380 km/h时，轮轨力第一主频增加到907 Hz，增幅为307 Hz。行车速度达到350 km/h时，轮轨系统的第一主频和次主频（30～60 Hz，环境振动的主要部分）以及所对应的幅值都显著增大。

（2）Vossloh300型扣件胶垫刚度的频变特性主要影响CRH380型高速动车组轮轨系统中心频率40～100 Hz部分，使得传递到路基的振动增大，扣件力的最大增幅为30.98%，并使该频率范围内的轮轨系统振动增加了2 dB，不考虑扣件胶垫刚度的频变特性将会低估轮轨系统40～100 Hz的中高频振动，同时会略高估710～900 Hz的高频振动。

（3）Vossloh300型扣件胶垫刚度频变特性对CRH380型高速动车组轮轨系统高频振动影响较小，在进行高频振动分析时可不予考虑其频变特性。但对于胶垫，不仅刚度具有频变特性，其阻尼也具有频变特性。因此，为精确预测高速铁路车辆及轮下结构随机振动的频域响应，数值仿真时需同时考虑扣件胶垫等高分子减振材料的刚度和阻尼频变特性。

[1] 韩坤. 高速列车高频振动特性分析[D]. 北京：北京交通大学，2011.

[2] JONES D I G. Handbook of Viscoelastic Vibration Damping[M]. New York：John Wiley&Sons，2001.

[3] 肖俊恒. 减振橡胶设计方法的研究[J]. 中国铁道科学，2001，22(6)：111-116.

[4] CARRASCAL I A，CASADO J A，POLANCOJA，et a1. Dynamic behavior of railway fastening setting pads[J]. Engineering Failure Analysis，2007，14(2)：364-373.

[5] 韦凯, 杨帆, 王平，等. 扣件胶垫刚度的频变性对地铁隧道环境振动的影响[J]. 铁道学报，2015，37(4)：80-86.

[6] 李莉，土书卫，吕英康，等. 钢轨扣件减振橡胶动态刚度特性分析[J]. 同济大学学报：自然科学版，2013，41(2)：208-212.

[7] MAES J，SOL H，GUILLAUME P. Measurements of the dynamic rail pad properties[J]. Journal of Sound and Vibration，2006，293(3-5)：557-565.

[8] 翟婉明. 车辆-轨道耦合动力学[M]. 4版. 北京：科学出版社，2015.

[9] 国家铁路局. TB/T 3395.1—2015高速铁路扣件[S].北京：中国铁道出版社，2015.

[10] 孙文静，周劲松，宫岛. 基于Timoshenko梁模型的车辆-轨道耦合系统垂向随机振动分析[J]. 机械工程学报，2014(18)：134-141.

[11] 陈镕，万春风，薛松涛，等. Timoshenko梁运动方程的修正及其影响[J]. 同济大学学报：自然科学版，2005(6)：711-715.

[12] 徐志胜，翟婉明，王开云，等. 车辆-轨道系统振动响应分析：Timoshenko梁与Euler梁轨道模型的比较[J].地震工程与工程振动，2003(6)：74-79.

[13] 徐志胜，翟婉明，王开云. 基于Timoshenko梁模型的车辆-轨道耦合振动分析[J]. 西南交通大学学报，2003(1)：22-27.

[14] ZUO S L, LI F M，ZHANG C. Numerical and experimental investigations on the vibration band-gap properties of periodic rigid frame structures[J]. ActaMech，2016，227(6)：1 653-1 669.

[15] Li F M，Liu C C. Vibration analysis and active control for frame structures with piezoelectric rods using spectral element method[J]. Archiveof AppliedMech，2015(5)：675-690.

[16] THOMPSON D J，VERHEIJ J W. The dynamic behaviour of rail fasteners at high frequencies[J]. Applied Acoustics, 1997, 52(1)：1-17.

[17] FENANDER A. Frequency dependent stiffness and damping of railpads[J]. Proceedings of the Institution of Mechanical Engineers：Part F: Journal of Rail and Rapid Transit，1997，211(1)：51-62.

[18] 国家铁路局. TB/T 3352—2014高速铁路无砟轨道不平顺谱[S]. 北京：中国铁道出版社，2014.

[19] 吕关仁. 京沪高速铁路轨道动静态几何状态变化分析[J]. 中国铁路，2014(6)：28-31.

责任编辑 李葳

lnfuence of Frequency-dependent Rigidity of Rubber Cushion of Vossloh300 Fastening to HSR High Frequency Vibration

DOU Yinling1，2，YANG Qilu1，2，WANG Ping1，2
（1. Key Laboratory of High-Speed Railway Engineering，Ministry of Education，Chengdu Sichuan 610031，China；2. School of Civil Engineering，Southwest Jiaotong University，Chengdu Sichuan 610031，China）

The rubber cushion of Vossloh300 fastening is chosen as the study object and put in the universal test machine equipped with the temperature box to get its static rigidity under 20 ℃. A random vibration analysis model of vehicle-track vertical coupled system is built up based on the Theory of Timoshenko Beam to explore the infuence of frequency-dependent rigidity of the rubber cushion of Vossloh300 fastening to the random vibration frequency domain of wheel-rail system within diferent frequency bands. The test result is as follows: the rigidity of the rubber cushion of Vossloh300 fastening under 3～5 Hz shock excitation is 22.4 kN/mm. The simulation analysis shows that the infuence of frequency-dependent rigidity of the rubber cushion of Vossloh300 fastening to the high frequency vibration of wheel-rail system of CRH380 high speed train is comparatively small, while the infuence to the center frequency of 40～100 Hz of 1/3 frequency doubling is big. The maximum amplifcation of the fastening reaches 30.89% and the vibration of track structure is increased by 2dB. Therefore, the frequencydependent rigidity of the rubber cushion shall be taken into consideration for wheel-rail vibration analysis.

wheel/rail system；frequency-dependent rigidity；rubber cushion of Vossloh300 fastening；high frequency vibration；Timoshenko Beam model；irregularity of track

U211.3

：A

：1001-683X（2017）07-0068-07DOI：10.19549/j.issn.1001-683x.2017.07.068

2017-02-16

国家自然科学基金高铁联合

（U1434201）；

高速铁路轨道技术国家重点实验室（中国铁道科学研究院）开放课题基金资助项目（2015YJ005）

豆银玲（1993—），女，硕士研究生。

E-mail：douyinling@my.swjtu.edu.cn