冷链物流网络的无标度特性研究
2017-08-16过秀成
胡 钢,张 华,徐 翔,过秀成
(1.安徽工业大学管理科学与工程学院, 安徽马鞍山 243032; 2.东南大学交通学院,南京 210096)
冷链物流网络的无标度特性研究
胡 钢1,2,张 华1,徐 翔1,过秀成2
(1.安徽工业大学管理科学与工程学院, 安徽马鞍山 243032; 2.东南大学交通学院,南京 210096)
论文对冷链物流网络进行无标度特性研究。首先,分析了冷链物流网络合作关系特性,发现新增节点在选择原有节点时并不完全按照原有节点的度,且冷链物流网络边不仅可增加还可以有删除;其次,对BA模型进行改进,在原有节点度作为择优指标的基础上引入新影响因素,构建相应择优概率,并依据客户中转遗失比例,按相应比例以反择优概率进行边的删除,建立了冷链物流网络模型;通过动力学分析冷链物流网络节点度分布规律,结论符合原始BA模型的幂率指数;最后,通过案例证明冷链物流网络模型符合无标度网络的分布特性。
无标度网络;冷链物流;幂率分布
随着需求量的增加,冷链物流已成为推进我国物流产业发展的支柱之一。我国是冷链食品生产和消费大国,东西南北中不同区域的冷链物流需求与供给差异性非常大,特种冷链物流跨区域运输与配送耦合性比较差,导致冷链物流的各个环节没能较好地衔接起来,无法形成系统的网络,效率低。如何构建有效的冷链物流网络,提高冷链货物,如北方的牛羊肉、瓜果鲜蔬,南方的鸡鱼鸭,跨区域均衡高效地运输与配送,是我国的冷链物流发展目前面临的核心问题之一。
本文就冷链物流网络的无标度网络建模与冷链网络无标度特性进行研究,根据企业冷链物流统计数据,证明冷链物流网络符合无标度网络的分布特性。本文的研究对进一步研究我国冷链物流网络特点,构建冷链物流运输与配送有着一定的指导意义。
一、国内外研究现状
(一)无标度网络理论发展演化
目前,应用无标度网络理论与方法对冷链物流方面的研究比较少。对物流网络及冷链物流网络的研究,国内外还处于初步阶段。
Barabási和Albert[1]于1999年首次提出的无标度网络概念,是复杂网络理论发展的里程碑,它扩展了复杂网络理论;2002年,Barabási和Albert[2]又证明了无标度网络的增长和择优连接的特性。Meepetchdee等[3]对第三方物流网络的特性进行分析研究,结合无标度网络特性,对第三方物流网络进行优化仿真,得出第三方物流网络优化方案。Thadakamalla 等[4]发现供应链网络的形成过程中网络节点的度符合幂率分布,得出供应链网络符合无标度网络特性的结论。
无标度网络是一种具有特殊性质的复杂网络,即无标度网络的节点度分布符合幂率分布。但是无标度网络符合复杂网络的基本特征,所以对复杂网络在物流方面的研究有助于无标度网络在物流方面的研究。然而,目前尚缺乏进一步通过无标度网络特性对物流网络,尤其是冷链物流网络的研究。
舒盼盼等[5]研究复杂网络的分形尺度特性,发现分型无标度网络结构上的节点传播影响力的区分度与分形维度有关,对实际病毒传播上的预警控制有着研究意义。杨芳等[6]在构建生鲜农产品冷链物流系统模型上对模型的主要功能进行了介绍。李靖等[7]通过分析物流网络的基本特性,得出物流网络基本符合复杂网络一般特性的结论,并利用复杂网络理论对物流网络局部互动关系与物流网络稳健性及全局演化关系进行了探究。刘毅等[8]探究并证明了物流外包网络具有复杂网络的基本特性。付洁[9]利用复杂网络理论分析腹地物流园区贸易的性质,建立贸易复杂网络模型,并验证其模型的优化效果。谭波[10]比较分析物流配送网络与无标度网络规律,得出物流配送网络符合无标度网络特性。张旭凤等[11]对物流配送网络的无标度特性进行分析,利用病毒传播机理建立配送节点服务客户饱和度模型。袁铭[12]研究了现实世界网络存在的层级结构,建立了一种级联失效模型,该模型对于物流网络设计有一定的指导意义。
在对BA模型进行改进的国内外研究中,有部分是对BA模型中增加删除节点的研究[13-15]。陶少华等[16]在原有BA模型的基础上,提出了一种在择优概率中添加吸引子的改进模型,得到了较为广泛的关注;邓凯英等[17]在吸引子模型的基础上提出随机吸引子模型。田生文等[18]提出一种基于聚类效应节点吸引力的复杂网络模型,并利用仿真实验证明该模型符合无标度特性,并具有较高的聚类系数。王建伟等[19]对BA模型中的增长方式进行了改进,提出批量节点增长方式,并验证了改进模型的无标度特性及小世界特性。Li等[20]对无标度网络的增长概率进行了修改。
通过分析总结冷链物流网络和无标度网络的相关文献,得出以下结论:
a)国内外对复杂网络和物流网络的研究,主要探讨物流网络特性与复杂网络特性的相似性,证明物流网络符合复杂网络。
b)国内外研究无标度网络的节点性质和平均路径长度;研究物流配送网络具有无标度网络的一些特征,但缺少对冷链物流网络是否符合无标度网络特性研究。
c)国内外对于BA模型的研究中,建立了更加符合现实网络形成过程的改进模型,但对具体网络模型的现实应用中缺少研究。
d)在对冷链物流网络的研究中,在无标度网络的建模过程中缺少考虑冷链物流的特殊性。因此,本文对冷链物流的特性进行了分析,在BA模型的基础上建立了更加符合冷链物流特性的模型,并利用现实案例对冷链物流的无标度网络特性进行了分析研究。
(二)无标度网络BA模型分析
BA模型1999年由Barabási和Albert首次提出[1],其模型假设与符号体系如下:
a) 初始状态:初始状态是一个节点数为m0的全连通网络;
b) 增长方式:每个时间间隔T增加一个新节点和新节点的m条边,m≤m0;
c) 优先连接:每个新节点与原有节点的连接概率P和原节点的度有关,其中优先概率P和原节点度的关系为:
(1)
式(1)中k表示网络中节点的度,i,j表示网络中节点,ki,kj分别表示节点i和j的度。
按照BA模型建立的网络度分布要符合幂率分布,且幂指数维持在3左右。原始BA模型的建立过程中只有节点加入,不涉及节点的删除[2]。而冷链物流网络中存在由于服务能力、服务水平及覆盖范围的成本等因素影响,导致客户放弃继续冷链网络合作关系的可能。为此,本文所研究的BA模型也涉及节点的删除。
二、冷链物流网络模型构建
(一)冷链物流网络的特性分析
冷链物流网络就是为保持其品质特性而采用的,从生产到消费的过程中始终处于低温状态的物流网络。
本文在建立冷链物流网络模型中,按照冷链物流网络的特性将无标度网络BA模型加以改造。在冷链物流网络发展过程中,物流网络上关联的客户与供应商之间通过大量的物流、资金流、信息流不断交换建立稳定的合作关系,同时不断有合作关系废止。鉴于此,本文对冷链物流网络模型中节点的连接与删除进行分析。对合作关系的解除即为节点之间连接边的删除,删除的边数按照现有客户转为遗失客户的统计概率。对于冷链物流网络,其节点之间的连接关系(即合作关系)直接影响节点度,对于分析冷链物流网络的无标度特性具有现实意义,而单纯的删除节点的操作不符合冷链物流网络中的合作关系变化规律,对冷链物流网络没有太多现实意义,所以在冷链物流网络中,与供应链、客户建立合作关系和解除合作关系在无标度网络中用边的删除来解释。
冷链物流网络模型的建立具体步骤如下:
a)初始状态:初始状态下,设冷链物流网络中有n0个节点、m0条边。
b)增长方式:设每经过单位时间步长增加1个节点,并与已有的m(m≤m0)个节点相连接。鉴于冷链物流网络的特殊性,其择优规则并不完全按照BA模型的择优概率P进行连接。另外,冷链网络上节点属性的多样性与复杂性,如节点处的服务质量、服务水平及服务半径范围等,这里新引入节点影响因素C,设其连接概率为:
(2)
式(2)中a、b为调节系数,a+b=1。
冷链物流网路在引入新客户,建立新合作关系,实现网络新连接边的同时,原网络中部分服务客户可能在解除合作关系,删除原来网络上的连接边。设:
若δ(0<δ<1)表示现有客户转为遗失客户的比例,则δm为新增节点中按照反择优概率删除的边数,其中,反择优概率:
(3)
N(t)表示t时刻网络节点数:
N(t)=t+n0
(4)
则t时刻网络中的边数:
E(t)=m0+(m-δm)t
(5)
(二)冷链物流网络模型度分布分析
设ki(t)表示t时新增节点i的度数,根据模型演化规则,运用连续介质理论和平均场理论,推导出冷链物流网络的节点i的度分布。
a) 择优生长,增加1个新节点与网络中原有的m(m≤m0)个节点连接,连接概率按照综合连接概率∏i=aC+bP(a+b=1)连接。此时的节点度i的变化率:
(6)
b)删除节点,按照概率P′删除δm条边。变化率为:
(7)
综合式(6)和式(7),得到ki(t)对t的变化率为:
(8)
求出度分布,由于冷链物流网络中t值远远大于其他值,因此变化率:
(9)
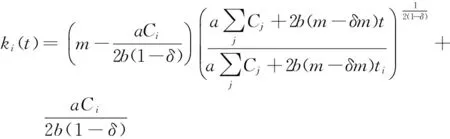
(10)
(11)
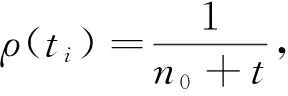
(12)
通过式(10)计算节点度的概率密度为:
(13)
令t→∞,得到稳态节点度分布:
(14)

当δ=0,Ci=0,则ρ(k)=2mk-3幂率指数为3,符合原始BA模型的幂率指数,而在冷链物流网络中,现有客户转为遗失客户的比例δ将直接影响冷链物流网络的幂率指数,进而影响冷链物流网络的形成规模;影响因素C将直接影响连接概率,对各个节点的度分布情况及网络性质有着一定的影响。
企业在建立冷链物流网络的过程中,在物流中心选址和供应商选择时,不仅需要进行规模分析,也需要考虑其他影响因素,例如物流中心服务范围、服务质量,以及供应商的产品质量等影响因素;另外,服务质量直接影响客户的遗失比例,也将直接影响冷链物流的形成规模。
三、实例分析
上述对BA模型进行改进的前提是冷链物流网络符合无标度网络的特性,即幂率分布。由于计算机模拟只能计算出瞬态平均度分布,得不到稳态平均度分布[22],现结合实例对冷链物流网络的特性符合无标度网络进行证明。
ZM公司是一家上海的冷链物流公司,在全国各个省份拥有大量的物流中心,其冷链物流网络范围广阔。设在其建立冷链物流网络中,各个物流中心就是冷链物流网络的节点,各个物流中心之间直接产生合作关系即为冷链物流网络的边。因案例是为了证实冷链物流网络的无标度特性,即分析冷链物流网络节点的度分布情况,故目前不考虑其物理属性与社会的属性。
设ZM公司建立的冷链物流网络边是表示冷链物流中心或节点之间产生的直接业务关系,该业务关系看作是网络合作博弈利益均衡后产生的完全信息下的合作关系,可看作是无向图网络,各个节点之间连接边是无向边。
在建立其冷链物流网络的过程中,由于数据量太大,本文利用滚雪球方法获取众多数据中的一部分。首先选取一到多个网络节点作为初始对象;然后通过对初始对象数据进行采集,主要获取与初始对象直接产生关联的对象;接着将与初始对象关联的对象列入初始对象中;重复上述步骤,直到没有新的对象的信息或者已获得足够量的研究对象为止。冷链物流网络如图1所示。
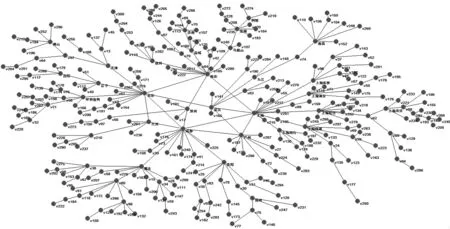
图1 冷链物流网络
通过网络分析专业软件Pajek对冷链物流网络进行分析。通过对冷链物流网络的节点的度进行分析得出结果见表1。
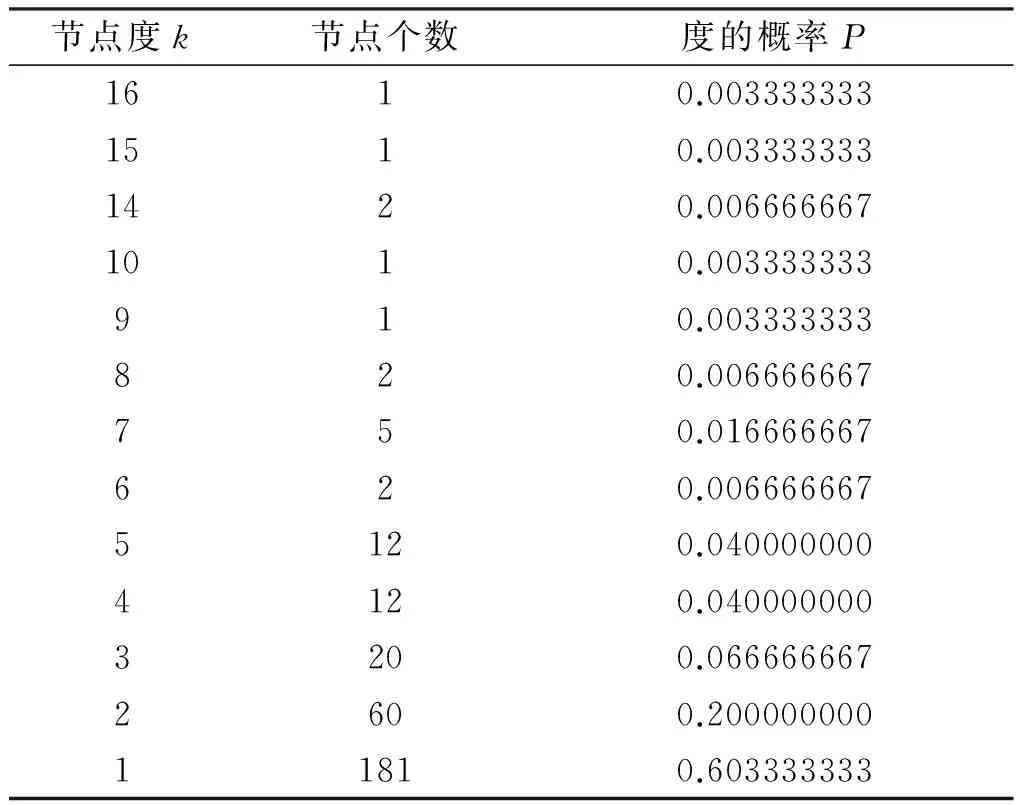
表1 节点度分布统计
通过对以上统计的数据进行绘制冷链物流网络的节点度幂率分布图(如图2)。
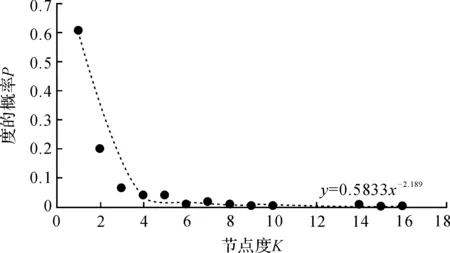
图2 冷链物流网络的节点度幂率分布图
通过分析软件得出冷链物流网络的节点的度分布符合幂率分布,其中的分布规律大致符合函数y=0.5833x-2.189的分布曲线,由此可以得出冷链物流网络符合无标度网络的特性,所以可以用此冷链物流网络模型模拟现实冷链物流网络。
四、结 语
本文首先基于冷链物流网络特殊性分析,通过增加影响因素对经典BA模型改进择优概率模型。结合冷链物流网络节点增加,同时也面临部分节点删除的特点,建立了符合冷链物流网络的模型。同时证明所建立的冷链物流网络模型的度分布符合幂率分布,当影响因素和客户遗失率都为零时,该模型完全符合BA模型的规律;并通过度分布公式的结果,对冷链物流企业提出相应的意见和建议。其次,通过建立冷链物流网络,并通过Pajek软件对冷链物流网络的节点的度分布情况进行统计分析,绘制出冷链物流网络的节点度分布图,结果显示冷链物流网络符合无标度网络的特性。从理论上为无标度网络在冷链物流网络上的应用和研究提供了理论依据。
[2] ALBERT R, BARABSI A. Statistical mechanics of complex networks[J]. Reviews of Modern Physics,2002,287:2115.
[3] MEEPETCHDEE Y, SHAH N. Logistical network design with robustness and complexity considerations[J]. International Journal of Physical Distribution & Logistics Management,2007,37(3):201-222.
[4] THADAKAMALLA H P, ALBERT R, KUMARA S R.Search in weighted complex networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics,2005,72(2):137-159.
[5] 舒盼盼,王伟,唐明,等.花簇分形无标度网络中节点影响力的区分度[J].物理学报,2015,64(20):441-451.
[6] 杨芳,谢如鹤.生鲜农产品冷链物流系统结构模型的构建[J].系统工程,2012(12):99-104.
[7] 李靖,张永安.复杂网络理论在物流网络研究中的应用[J].中国流通经济,2011,25(5):38-42.
[8] 刘毅,汝宜红,张晶.复杂网络视角下物流外包网络的结构特征[J].物流技术,2015(4):174-176.
[9] 付洁.腹地物流园区贸易复杂网络优化研究[D].大连海事大学,2011.
[10] 谭波.基于无标度网络的配送网络演化规律探究[J].物流技术,2015,34(6):136-139.
[11] 张旭凤,张永安.物流配送网络的无标度网络特征研究[C]∥中国工业企业物流论坛.2011.
[12] 袁铭.带有层级结构的复杂网络级联失效模型[J].物理学报,2014(22):73-80.
[13] 陈禹,宗骁,郝杰,等.BA模型的三种扩展[J].系统工程学报,2005,20(2):120-127.
[14] 辜芳琴,樊锁海.BA无标度网络的双向演化模型[J].暨南大学学报(自然科学与医学版),2013,34(5):475-478.
[15] 刘捷.无尺度网络建模仿真与分析[J].武汉理工大学学报,2006,28(9):108-111.
[16] 陶少华,杨春,李慧娜,等.基于节点吸引力的复杂网络演化模型研究[J].计算机工程,2009,35(1):111-113.
[17] 邓凯英,邓竞伟,李应兴.改进的BA网络演化模型的研究及应用[J].计算机系统应用,2012(8):114-117.
[18] 田生文,杨洪勇,李阿丽,等.基于聚类效应节点吸引力的复杂网络模型[J].计算机工程,2010,36(10):58-60.
[19] 王建伟,荣莉莉,于凯.基于节点批量生长机制的无标度网络演化模型[J].系统工程学报,2010,25(5):579-584.
[20] LI K, ZHENGHENG B J, DEYI L I, et al. A fractal and scale-free model of complex networks with hub attraction behaviors[J]. Science China,2015,58(1):1-10.
[21] 郭进利,汪丽娜.幂律指数在1与3之间的一类无标度网络[J].物理学报,2007,56(10):5635-5639.
[22] 郭进利.新节点的边对网络无标度性影响[J].物理学报,2008,57(2):756-761.
(责任编辑: 钱一鹤)
Research on Scale-free Characteristics of Cold Chain Logistics Network
HUGang1,2,ZHANGHua1,XUXiang1,GUOXiucheng2
(1.School of Management Science & Engineering, Anhui University of Technology, Ma’anshan 243032, China; 2.School of Transportation, Southeast University, Nanjing 210096, China)
The scale-free characteristic of cold-chain logistics network is studied in this paper. Firstly, cooperation relationship characteristic of the cold-chain logistics network is analyzed. It is found that the new node is not entirely in accordance with the degree of the original node, and the edge of cold-chain logistics network can not only be increased, but be deleted. Secondly, the BA model is improved. Based on the original node degree as the optimal index, the new influencing factor is introduced for constructing the corresponding optimal probability. According to the proportion of lost customers in transit, the edge is deleted with the inverse optimal probability based on the corresponding proportion, and the cold-chain logistics network model is established. The distribution law of node degree of cold-chain logistics network is analyzed by kinetic method, and the results are in agreement with the power law exponent of the original BA model. Finally, a case study shows that the cold chain logistics network model conforms to the distribution of scale-free network.
scale-free network; cold chain logistics; power law distribution
10.3969/j.issn.1673-3851.2017.04.006
2016-10-18 网络出版日期:2017-03-28
安徽省哲学社会科学规划项(AHSK11-12D74);国家自然科学基金项目(51368055)
胡 钢(1970-),男,甘肃天水人, 副教授, 博士,主要从事物流工程、决策分析方面的研究。
N945.12/F251.1
A
1673- 3851 (2017) 02- 0127- 06
