基于DS证据理论的多幅遥感影像融合去噪

黄冬梅,朱贵鲜,张明华*,王丽琳,苏 诚

(1.上海海洋大学信息学院,上海201306;2.国家海洋局东海预报中心,上海200137)

基于DS证据理论的多幅遥感影像融合去噪

黄冬梅1,朱贵鲜1,张明华1*,王丽琳2,苏 诚2

(1.上海海洋大学信息学院,上海201306;2.国家海洋局东海预报中心,上海200137)

针对目前单幅遥感影像去噪方法会过度扼杀影像边缘信息或噪声去除不理想问题,提出了一种基于DS (Dempster-Shafer)证据理论的多幅遥感影像融合去噪方法。DS证据理论结合多源信息,能够有效处理不确定性问题,适用于噪声具有随机性和不确定性情景。本文采用Landsat8卫星获取的上海周边海域遥感数据,依据DS证据理论处理不确定问题的优势,并充分利用多幅遥感影像的有效信息,设计4个模型,即两状态高斯混合模型、两个噪声分析模型、边缘分析模型。这4个模型用以获取每个像素与噪声相关的概率,作为证据理论的4个证据,用于决策去噪方案。结果表明,本文提出的多幅遥感影像融合去噪方法在保证去除噪声的情况下能较好地保持影像边缘和纹理细节信息。

遥感影像;DS证据理论;影像融合;影像去噪

遥感影像在获取和传输的过程中容易受到噪声的污染,被污染的影像会影响它的进一步处理,对影像的理解和识别带来一定的困难[1]。研究表明,在一幅影像中,当信噪比低于一定程度时,在影像分割时产生的误检概率增大,在参数估计时误差增大;在区域数的确定上,容易过估区域的数目[2]。因此,在对遥感影像进行边缘检测、参数估计、特征提取、信息分析和模式识别等处理之前,依据容许的性能采用适当的降噪方法改善、提高影像质量是一个非常重要的环节[3]。

遥感影像大多数像素的灰度值差别不明显,正是由于这种灰度相关性的存在,一般遥感影像的能量主要集中在低频区域,只有影像的细节部分的能量处于高频区域[4]。同时,噪声的能量也处于高频区域,而去除噪声的主要方法就是消除或衰减高频分量、增强低频分量,因此遥感影像在消减噪声的过程中,影像的细节也有一定程度的衰减[5]。这也是目前去噪方法存在的一个问题,即去除噪声与保持影像细节信息之间的矛盾。传统的去噪方法一般在单幅影像内基于影像空间相关性进行平滑滤波(如高斯滤波、中值滤波、均值滤波)[1,6],或基于频域[7]、小波域[8-14]以及其他方法[15]进行滤波等。由于空域滤波仅根据影像的空间相关性判断影像的某像素是否为噪声,而不考虑时域信息[16],因而不好把握影像的全局特征。小波域去噪方法主要利用小波基对影像进行多尺度变换,由于信号突变点在不同尺度的同一位置都有较大的峰值出现,噪声能量却随着尺度的增大而减小,因此能够提高信号边缘的定位精度,更好地刻画真实信号。但其在实际应用时,如何选择最优阈值是一个很大的难题。其他降噪方法主要思想是如何建立合理的目标分类函数,将噪声和有用信号分为两个子空间,去除噪声空间从而得到降噪后的影像[3]。

作为优秀的图像去噪方法,小波阈值去噪被很多研究者所选择。为解决最优阈值不易选择的问题,黄剑玲和郑雪梅[5]先通过小波边缘检测,确定边缘信息在各个子带中的位置,预先保留影像的边缘特征,以便尽可能根据噪声方差来设定阈值而不必担心损害影像的边缘特征。但对于同一幅含噪影像,正确地提取边缘而不受噪声影响比较困难。孙雷等[17]利用高光谱遥感影像的多个波段,用含噪较少的波段辅助含噪多的波段融合去噪,但对于波段相差较大的多光谱影像,会引入辅助波段的光谱信息,带来新的噪声,即便是高光谱影像,如果两个波段离得比较远也会引入光谱噪声。以上两种方法体现了单幅遥感影像去噪的局限性,给予多幅遥感影像融合去噪的启示。同时,随着遥感技术的迅猛发展,使得遥感具有三高(高空间分辨率、高光谱分辨率、高时相分辨率)和三多(多传感器、多平台、多角度)的特点,为多幅遥感数据处理提供了数据基础。本文提出基于信息融合的思想、采用DS证据理论对多幅遥感影像进行融合去噪。将针对同一目标的多幅遥感影像数据加以智能化合成,从而产生比单一数据源更精确、更完全的估计和判决。杨海峰和侯朝桢[18]利用DS证据理论的合成法则对初始小波萎缩系数进行修正、重构,Lin[19]根据单幅遥感影像的空间相关性,设置了4个证据利用DS证据理论对其融合,得到该像素是否为噪声的结论,虽然仍面临单幅影像去噪阈值不易确定或权重不易设置问题,但都体现了DS证据理论在人工智能范畴通过信息融合处理知识不准确因素引起的不确定问题的能力。

(王 燕 编辑)

结合上述方法的优缺点,依据遥感影像噪声在小波域和空间域的不同表现特征,本文为每幅遥感影像分别在小波域和空间域建立4个噪声提取模型,通过DS证据理论信息融合技术,融合4个模型的统计结果及多时相遥感影像的多源信息,得到多幅遥感影像证据融合结论,决策去噪。该方法充分利用多幅遥感影像的信息,实验结果证实了该方法的有效性。

1 DS证据理论基本原理

DS证据理论是Dempster和Shafer于二十世纪六七十年代发展、完善形成的一种推理理论[20]。DS证据理论通过合并多重证据从而做出决策,对推理进行合理的信息论解释,是一种决策理论。与概率决策理论相比,它不但能够处理由于知识不准确引起的不确定性,也能够处理由于不知道的因素引起的不准确性[20]。DS证据理论的基本原理[21]如下:

假设存在一个有限假设空间,Θ为空间中所有命题的穷举集合。DS理论用“识别框架”描述构成整个假设空间的所有命题的集合,识别框架中的各元素互相排斥,集合中的命题称为识别框架的原命题。本文方法的识别框架Θ为{数据与噪声相关(n),数据与非噪声相关(f)}。

1.1 基本概率分配

在识别框架Θ上的基本概率分配BPA(Basic Probability Assignment)是一个2Θ→[0,1]的函数m,称为mass函数,满足其中,在识别框架上使得m(A)＞0的A称为焦元。m(A)为命题A的基本概率赋值,表示对命题A的信任程度,比如某证人认为某像素是噪声的确认度,是DS证据理论多证据合成的关键依据。

1.2 Dempster合成规则

Dempster合成规则,也称证据合成公式,定义:

对于∀A⊆Θ,Θ上的两个mass函数m1,m2的Dempster合成规则为

n个mass函数的Dempster合成规则:

对于∀A⊆Θ,识别框架Θ上的有限个mass函数m1,m2,...,mn的Dempster合成规则为

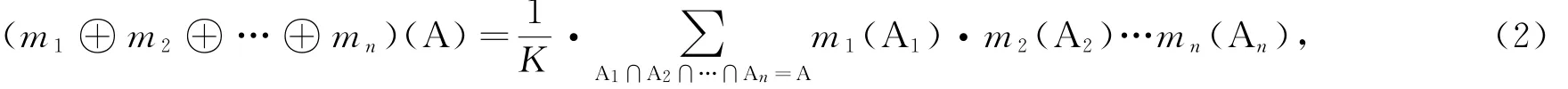
2 多幅遥感影像去噪方法

2.1 整体方案

本方案的关键问题是如何恰当的定义基本概率分配,因此需要一个方法表示证据并获得相应的mass函数。本文为每幅影像设置4个模型来获得基本概率分配,即:

证据1(两状态高斯混合模型),利用小波变化具有信号的突变点在不同尺度的同一位置都有较大的峰值出现的性质,而噪声能量却随着尺度的增大而减小的特点,来刻画小波系数是与噪声相关还是与边缘相关的概率。

证据2(空间相关噪声分析模型1),设置n*n窗口,对窗口中数据排序取中间值,根据中心值与中间值的差异程度决定中心值为噪声的概率。

证据3(空间相关噪声分析模型2),设置n*n窗口,对窗口中的数据求平均值,根据中心值与平均值的差异程度决定中心值为噪声的概率。

证据4(边缘分析模型),考虑窗口中属于边缘的元素对证据2和证据3也会得到较大的概率值,容易把边缘误分为噪声,设计了边缘分析模型,根据窗口中与中心值差异最小的3个值的差异程度决定是噪声的概率。

本文方法具体实施时,首先选取同一位置某一时间段的多幅遥感影像,然后对每幅影像对应波段进行多个模型下的数据统计分析,并得到每个模型下每个像素点是噪声的概率,作为DS证据理论的基本概率分配;然后使用DS证据理论证据组合规则将4个证据组合成一个证据,得到每幅影像每个像素点是噪声的概率,作为多幅遥感影像融合去噪的基本概率分配;重复使用DS证据理论的证据组合规则,将多幅遥感影像相应波段的信息融合起来,得到多幅遥感影像融合mass函数;计算出信任区间,并利用设计好的决策规则进行去噪,得到融合去噪的影像。本方案整体流程如图1所示。

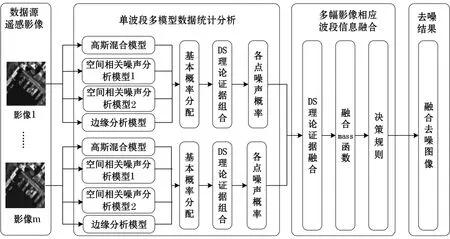
图1 基于DS证据理论的多幅遥感影像融合去噪流程Fig.1 Process of de-noising based on DS evidence theory using multiple images

2.2 基本概率分配定义

2.2.1 证据1基本概率分配的定义

建立两状态高斯混合模型,两状态指小波系数与边缘相关还是与非边缘相关。对小波系数用隐马尔可夫模型训练,得到系数属于边缘或噪声的概率,及两状态模型下各分解尺度的两状态方差,进而得到两状态下的条件概率,得到证据1的基本概率分配。K状态高斯混合模型[22]如公式(3)所示。

式中,fj(sj)为状态密度函数Θ为DS理论的识别框架,本文中方法Θ为{noise(n),freenoise(f)},n表示噪声,f表示无噪声。按照此模型,BPA定义方式为

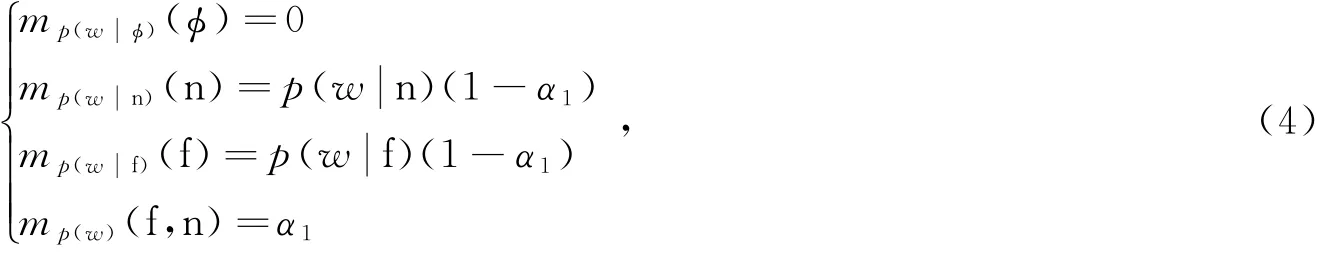
式中,α1表示支持不确定的信任度,mp(w|Θ)表示在两状态高斯混合模型p(w|Θ)下的mass函数,即基本概率分配。

为保证影像局部信息和空间相关性,以下3个证据采取小窗口形式,窗口大小为3*3。

2.2.2 证据2基本概率分配的定义

设中心点位置灰度值w(k),将除中心点位置的8个系数从大到小进行排序:r(1),r(2),r(3),r(4), r(5),r(6),r(7),r(8),取排序后的中间值,并求平均值ROM(k):

则窗口中心点为噪声的概率d(k)可表示为

d(k)越大,说明w(k)与周围灰度值差异越大,是噪声的可能性就越大。按照此模型,BPA定义方式如下:

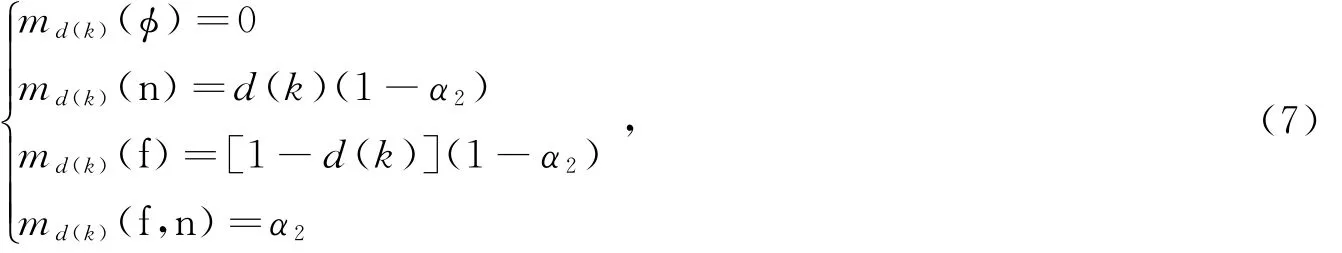
式中,α2表示支持不确定的信任度,md(k)表示模型d(k)下的mass函数,即基本概率分配。

2.2.3 证据3基本概率分配的定义

设i为灰度值对应位置编号,中心点位置灰度值w(k),则灰度值梯度δi可表示为

p(k)越大,说明w(k)与周围灰度值差异越大,按照此模型,BPA定义方式:

式中,α3表示支持不确定的信任度,mp(k)表示在模型d(k)下的mass函数,即基本概率分配。

2.2.4 证据4基本概率分配的定义

由于被污染的像素一般会引起较大的d(k)和较大的p(k)。但是如果没有被噪声污染的像素位于边缘,d(k)和p(k)也会相对较大。因此,本文又引入另一个证据o(k),以区分像素与边缘相关或是与噪声相关。

设i为灰度值对应位置编号,中心点位置灰度值w(k),中心点位置灰度值与位置i灰度值的差异ai可表示为

对ai进行从小到大排序,得到数组c,c=sort(a)。从ai表达式可以看出中心点与自身差异最小。若中心点属于边缘,即使在证据2和3得到了较大的d(k)和p(k),但根据边缘的连贯性,若像素与边缘相关,计算的结果就是,在窗口中同属边缘的灰度值差异ci比较小,也就可以引入概率o(k),检测具有较大d(k)和p(k)是噪声或是边缘。据此,o(k)定义如下:

o(k)越大,说明w(k)与他最接近的3个点差异越大,表示该点是噪声的可能性就越大;反之,该点是边缘的可能性越大。按照此模型,BPA定义方式:

式中,α4表示支持不确定的信任度,mo(k)表示在模型o(k)下的mass函数,即基本概率分配。

2.3 决策规则

本文中方法通过4个模型对遥感数据进行统计分析,并对统计数据在单幅影像下进行信息融合,作为多幅信息融合的输入。在第二次信息融合得到的融合mass函数基础上,遵循优先选择数据质量较好的数据的原则,遵循最大限度保存边缘信息的原则,制定最终去噪的决策规则,具体如下:

1)首先对每幅影像单个波段利用4个模型计算DS理论的4个基本概率分布;

2)利用DS理论的融合规则,把每幅影像的4个证据融合成一个整体的概率分布;

3)再利用DS理论融合规则,把2)得到的多幅遥感影像整体的概率分布融合成一个概率分布;

4)根据3)的融合结果,若某像素融合的结果是非噪声,且多个证据都是支持非噪声,选择支持非噪声概率大的证据;

5)若融合结果是非噪声,多个证据中一些证据支持某像素为噪声,说明支持非噪声的证据较强,选择支持非噪声大的证据;

6)若融合结果是噪声,多个证据中有支持某像素为非噪声的证据,说明支持噪声的证据较强,放弃支持噪声的证据,如果这时支持非噪声的证据大于某一值,则相信这个证据,否则对这个证据做萎缩处理,处理后的结果为最终像素值;

7)如果融合结果是噪声,所有证据都支持噪声,则选取支持噪声相对小的影像,取其平稳小波变化的低频系数重构,得到的灰度值为融合去噪后影像的灰度值。

3 结果与分析

本文采用遥感影像均方误差MSE(Mean Squared Error,MSE=和峰值信噪比PSNR(Peak Signal to Noise Ratio,PSNR=10 lg[(216-1)2/MSE])来度量去噪后的影像质量。MSE越小,PSNR越大,说明去噪的效果越好。

3.1 B4波段去噪实验结果

该实验选用了Landsat 8卫星获取的上海周边海域同一位置的两幅遥感影像的一个可见光波段(B4波段)对本文方案在去除高斯噪声上进行验证。为两幅遥感影像B4波段分别加入方差为0.000 1和0.005 db的高斯白噪声,将其作为两幅原始数据进行融合去噪,结果如图2至图4所示。

结果表明,本文方法(图2e)边缘保留较为清晰,也比较接近原始影像(图2a至图2b)。低通滤波(图3a,图4a)、纳维滤波(图3b,图4b)、中值滤波(图3c,图4c)、均值滤波(图3d,图4d)、小波阈值去噪(图3e,图4e),特别是低通滤波,去噪结果边缘比较模糊。

从参数上看,本文方法在峰值信噪比和均方误差两个指标上均优于其他5种方法。由表1可知,本文方法去噪得到的影像好于任一幅含噪影像;由表2和表3可知,融合去噪得到的影像具有最大的信噪比和最小的方差,远远好于含噪影像2(图2d)单幅影像的去噪结果(图4a至图4e),略好于含噪影像1(图2c)单幅影像的去噪结果(图3a至图3e),说明两幅影像融合去噪比单幅影像去噪更加有效。

图2 实验数据及本文方法去噪结果Fig.2 Experimental data and the de-noising results

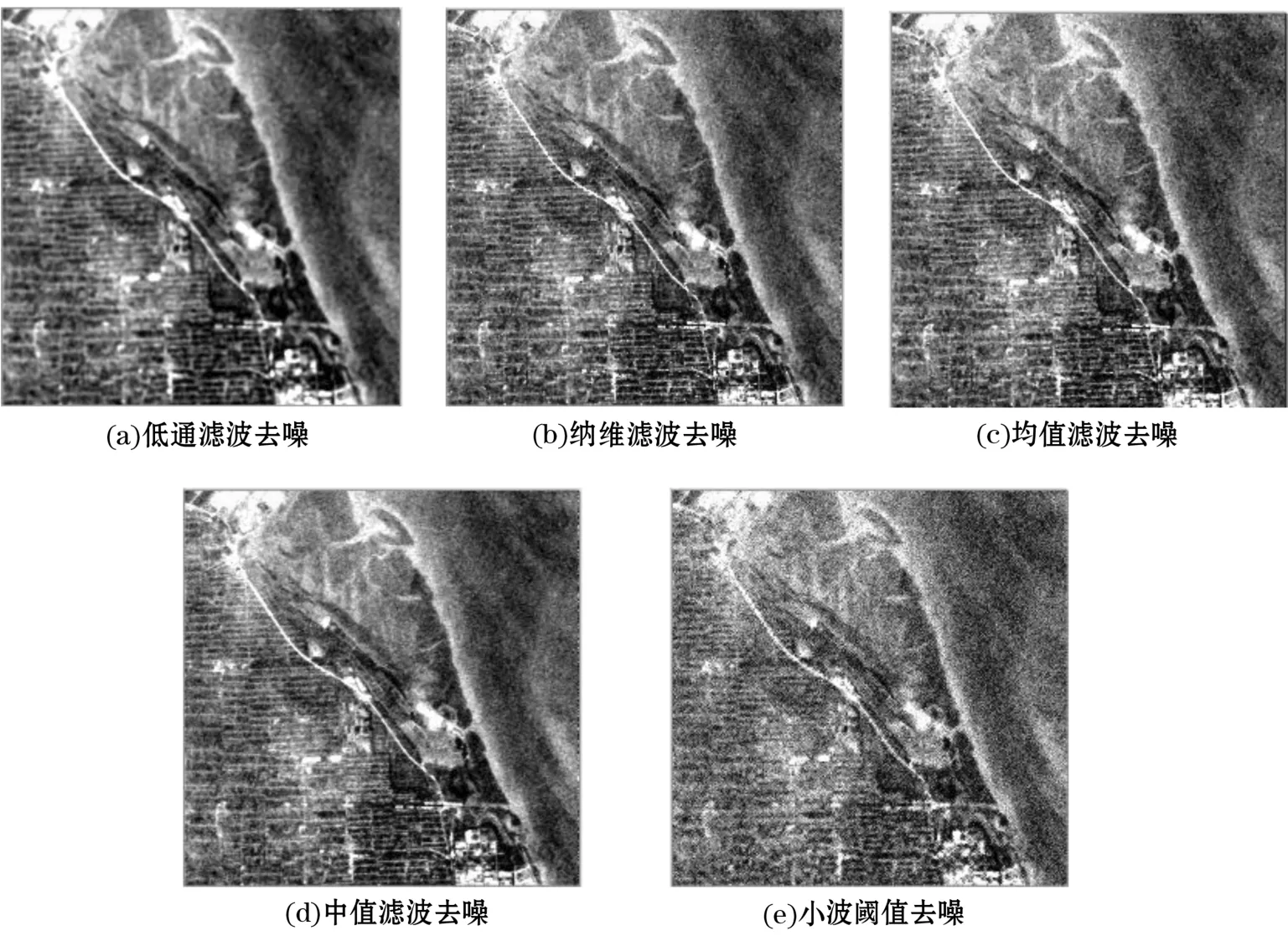
图3 对原始影像1 B4波段加入0.000 1 db高斯白噪声影像(图2c)的5种方法去噪结果Fig.3 De-noising results by applying five methods to the image shown in figure 2c,which was obtained by adding 0.000 1 db white Gaussian noise to the fourth band of raw image 1(figure 2a)

图4 对原始影像2 B4波段加入0.005 db高斯白噪声影像(图2d)5种方法去噪结果Fig.4 De-noising results by applying five methods to the image shown in figure 2d,which was obtained by adding 0.005 db white Gaussian noise to the fourth band of raw image 2(figure 2b)

融合去噪后影像的信噪比和方差与含噪影像2单幅影像各种方法去噪的结果差别较大,而与含噪影像1单幅影像各种方法去噪的结果差别不大。这是因为含噪影像1是加方差为0.000 1 db的高斯白噪声影像,较接近真实影像;而含噪影像2是加了方差为0.005 db的高斯白噪声影像,与真实影像差异较大。另外,实验数据源加入了某特定方差的高斯白噪声,在整幅影像中分布比较均匀,而自然环境下形成的噪声比较分散,一幅影像上某个位置含噪声,在另一幅影像该位置也含噪声的可能性比加入的均匀噪声相比小的多。因此,真实环境下本文的去噪方法在原则上会比添加均匀噪声的情况下去除噪声的效果更好。

表1 添加0.000 1 db(图2c)和0.005 db(图2d)高斯白噪声以及本文去噪方法获得影像(图2e)信噪比、方差对比Table 1 PSNR and MSE for the images shown in figures 2c,2d and 2e

表2 对原始影像1 B4波段加入0.000 1 db高斯白噪声影像(图2c)的5种方法去噪图像(图3)及本文方法去噪影像(图2e)信噪比、方差对比Table 2 PSNR and MSE for the images shown in figures 3 and 2e

表3 对原始影像2 B4波段加入0.005 db高斯白噪声影像(图2d)的5种方法去噪图像(图3)及本文方法去噪影像(图2e)信噪比、方差对比Table 3 PSNR and MSE for the images shown in figures 4 and 2e

3.2 B5波段去噪实验结果

该实验选用了与实验1相同位置的3幅不同光照强度遥感图像的不可见光波段(近红外B5波段)对本文方案在去除高斯噪声上进行验证。为3幅遥感影像B5波段分别加入方差为0.001,0.005和0.007 db的高斯白噪声作为两幅原始数据进行融合去噪。实验结果如图5至图7所示。

结果表明,本文方法(图5g)边缘保留较为清晰,也比较接近原始影像(图5a至图5c)。低通滤波、纳维滤波、中值滤波、均值滤波、小波阈值去噪,特别是低通滤波,去噪结果边缘比较模糊。

从参数上看,本文方法在峰值信噪比和均方误差两个指标上均优于其他5种方法。由表4可知,本文方法去噪得到的影像好于任一幅含噪影像;由表5和表6可知,融合去噪得到的影像具有最大的信噪比和最小的方差,说明3幅影像融合去噪比单幅影像去噪更加有效,得到了与B4波段去噪一致的效果。

表4 添加0.001 db高斯白噪声(图5d)、添加0.005 db高斯白噪声(图5e)、添加0.007 db高斯白噪声(图5f)以及本文去噪方法获得影像(图5g)影像信噪比、方差对照比Table 4 PSNR and MSE for the images shown in figures 5d,5e,5f and 5g

图5 实验数据及本文方法去噪结果Fig.5 Experimental data and the de-noising results

图6 对原始影像1 B5波段加入0.001 db高斯白噪声影像(图5d)的5种方法去噪结果Fig.6 De-noising results by applying five methods to the image shown in figure 5d,which was obtained by adding 0.001 db white Gaussian noise to the fifth band of raw image 1(figure 5a)

图7 对原始影像2 B5波段加入0.005 db高斯白噪声影像(图5e)的5种方法去噪结果Fig.7 De-noising results by applying five methods to the image shown in figure 5e,which was obtained by adding 0.005 db white Gaussian noise to the fifth band of raw image 2(figure 5b)

表5 对原始影像1 B5波段加入0.001 db高斯白噪声影像(图5d)的5种方法去噪图像(图6)及本文方法去噪影像(图5g)信噪比、方差对比Table 5 PSNR and MSE for the images shown in figures 6 and 5g

表6 对原始影像2 B5波段加入0.005 db高斯白噪声影像(图5e)的5种方法去噪图像(图7)及本文方法去噪影像(图5g)信噪比、方差对比Table 6 PSNR and MSE for the images shown in figures 7 and 5g

3.3 去云和雾实验结果

以上两个实验是本文方法对去除热噪声(由导体中电子的热震动引起的,它存在于所有电子器件和传输介质中,是温度变化的结果)、散粒噪声(通信设备中的有源器件中,由于电子发射不均匀性所引起的噪声)等高斯类型噪声的验证,也是本文研究的主要噪声。同时,考虑由于天气原因引起的噪声,比如云和雾,为另一类遥感影像处理的主要误差来源。目前的单幅遥感影像去云方法,主要是对薄云的弱化而不是去除,对厚云、大面积云的弱化效果则不是很理想。为了验证本文方法在去云和雾的可行性,设计了该实验。该实验选用了Landsat 8卫星获取的上海周边海域同一位置的含云或雾量不同的3幅遥感影像,对本文方法在主要研究的高斯噪声以外的噪声去除的验证。

由于本文方法主要研究的电噪声、散粒噪声等高斯噪声性质,2.2节的表示噪声的模型以及2.3节去除噪声的融合规则不完全适用于去除云和雾,因此仅保留了2.2节的模型1以及2.3节规则1)～5)进行的去云处理。在这种情况下,当多幅影像融合去噪的数据源为图8a和图8b时,两幅影像只含云噪声,其融合去云结果如图8d和表7所示。从表7可以看出,融合去云的结果好于去噪输入图像。这说明DS证据理论多幅影像融合去云模式的可行性,至于效果要看对云和雾建立专门的模型。与两个数据源融合相比添加了一幅既含大雾又含云的影像8c,融合结果把大雾也融合了进去,如图8e所示。这是由于雾的特征比较平滑,在噪声表述模型中代表比较好的数据,与高斯噪声类型的噪声相比性质差别比较大。因此,不能直接把表征高斯噪声的模型直接表征雾,表征雾的模型有待进一步研究。同时,从去云的效果来看,对大面积云的表述模型也有待进一步研究。这也是后续我们要做的工作。

表7 含云影像1,含云影像2,含云和雾影像3,含云影像1和2融合去噪影像以及含云影像1,2和3融合去噪影像(图8)信噪比、方差对照比(B4)Table 7 PSNR and MSE for the images contaminated by clouds and fog as well as the de-noising results

图8 含云和雾影像实验数据和去噪结果Fig.8 Experimental data with clouds or fog and the results of de-noising

4 结 语

DS证据理论作为人工智能的范畴,具有处理不确定信息的能力,被广泛应用于专家系统、目标识别、医学诊断、军事指挥等许多需要综合考虑来自多源的不确定信息,如多个传感器的信息、多位专家的意见等,以完成问题的求解,并适用于噪声具有随机性和不确定性情景。本文将DS证据理论引入到多幅遥感影像融合去噪问题中,拓展了单幅遥感影像去噪的范畴,将两幅或两幅以上具有互补信息的遥感影像,利用小波变化进行多层次分解,映射到不同分辨率上,由粗到细观察影像,并对影像的低频分量以及垂直方向、水平方向、对角线方向三个高频分量,同时从每幅影像的可信度及重要性多级别综合处理,得到更为精准、更具可靠性、且含有更丰富信息的影像。融合去噪后的遥感影像在减少模糊性的同时,具有更佳的互补性、可理解性,更加适合人类视觉或计算机检测、识别、分类、理解等影像处理。同时,在两状态高斯混合模型中,仅利用小波变换的分析功能,避开了直接使用小波阈值去噪阈值不易确定的问题。由于本文方法是对多幅影像相同波段间数据进行处理,使去噪过程避免引入不同波段的光谱噪声,且能充分利用多幅影像间的互补信息,得到信息更加丰富的影像。

本文去噪方法4个模型主要是针对高斯噪声。对于大面积云和雾处理,从实验结果可以看出,对两幅仅含云的影像融合运算,得到的是一幅更优的影像,说明多幅遥感影像融合去云的可取性;当再加入一幅含有大雾和少量云的输入后,融合运算结果有些混乱,效果有待提升。这与表征云和雾的模型有关,本文模型主要是针对热噪声、散粒噪声等高斯类型的噪声,对去云和雾的噪声表征模型正在做进一步的研究,希望后续找到一个模型的最小集,来去除尽可能的多类型噪声。

[1] LI J L,LI H J,XU Q.Non-local means denoising based on wavelet threshold[J].Computer Engineering and Science,2015,37(8): 1546-1550.李嘉浪,李华君,徐庆.基于小波阈值的非局部均值去噪[J].计算机工程与科学,2015,37(8):1546-1550.

[2] LEI T,UDUPA J K.Performance evaluation of finite normal mixture model-based image segmentation techniques[J].IEEE Transactions on Image Processing,2003,12(10):1153-1169.

[3] LI X C.Application of wavelet-domain markov random field in image processing[M].Beijing:Electronic Industry Press,2011.李旭超.小波域马尔可夫随机场在影像处理中的应用[M].北京:电子工业出版社,2011.

[4] LI C,GU X F.Wavelet image denoising in wavelet shrinkage ways[J].Journal of Remote Sensing,2006,10(5):697-702.李翀,顾行发.基于小波萎缩方法的影像小波去噪的研究[J].遥感学报,2006,10(5):697-702.

[5] HUANG J L,ZHENG X M.An optimized method for image denoising based on edge detection[J].Computer Simulation,2009,26(11): 260-263.黄剑玲,郑雪梅.一种基于边缘检测的影像去噪优化方法[J].计算机仿真,2009,26(11):260-263.

[6] REN H R,ZHANG P,WANG J L.A method of scanned image denoising based on morphological pyramid[J].Infrared Technology, 2004,26(2):40-43.任获荣,张平,王家礼.一种形态金字塔扫描图像去噪方法[J].红外技术,2004,26(2):40-43.

[7] XIA Q,XING S,MA D Y.An improved K-SVD-based denoising method for remote sensing images[J].Journal of Remote Sensing, 2016,20(3):441-449.夏琴,邢帅,马东洋.遥感卫星影像K-SVD稀疏表示去噪[J].遥感学报,2016,20(3):441-449.

[8] LI Q N,CHAO A N,SHI D Q,et al.A novel image denoising method of wavelet semi-soft threshold[J].Computer Engineering and Science,2014,36(8):1566-1570.李秋妮,晁爱农,史德琴,等.一种新的小波半软阈值影像去噪方法[J].计算机工程与科学,2014,36 (8):1566-1570.

[9] DONOHO D L,JOHNSTONE J M.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika,1994,81(3):425-455.

[10] CHANG S G,YU B,VETTERLI M.Adaptive wavelet thresholding for image denoising and compression[J].IEEE Transactions on Image Processing,2000,9(9):1532-1546.

[11] ZONG X L,GEISER E A,LAINE A F,et al.Homomorphic wavelet shrinkage and feature emphasis for speckle reduction and enhancement of echocardiographic images[J].Proceedings of SPIE-The International Society for Optical Engineering,1996,2710:658-667.

[12] JANSEN M,MALFAIT M,BULTHEEL A.Generalized cross validation for wavelet thresholding[J].Signal Processing,1997,56(1):33-44. [13] TASDIZEN T.Principal components for non-local means image denoising[C]∥15th IEEE International Conference on Image Processing.New York:IEEE,2008:1728-1731.

[14] ZHANG J Y,MA Y,TIAN Z,et al.Impact of wavelet denoising on multi-spectral bathymetry inversion[J].Advances in Marine Science,2015,33(3):334-341.张靖宇,马毅,田震,等.小波滤噪对多光谱遥感水深反演精度的影响分析[J].海洋科学进展,2015,33 (3):334-341.

[15] JIANG S P,HAO X J.Hybrid fourier-wavelet image denoising using gaussian scale mixture model for wavelet coefficients[J].Journal of Image and Graphics,2009,14(3):448-451.姜三平,郝晓剑.应用小波系数GSM统计模型的混合傅里叶-小波影像降噪[J].中国影像图形学报,2009,14(3):448-451.

[16] SONG B,XU C.The analysis of low SNR video de-noising algorithms using temporal domain and spatial domain mixture methods[J]. Infrared Technology,2011,33(8):489-494.宋博,徐超.基于时域和空域混合的低信噪比视频降噪算法及其分析[J].红外技术, 2011,33(8):489-494.

[17] SUN L,GU D F,LUO J S.Hyperspectral imagery denoising method based on wavelets[J].Spectroscopy and Spectral Analysis,2009, 29(7):1954-1957.孙雷,谷德峰,罗建书.高光谱遥感影像的去噪方法[J].光谱学与光谱分析,2009,29(7):1954-1957.

[18] YONG H F,HOU C Z.Image de-nosing by wavelet shrinkage based on evidence theory[J].Optical Technique,2005,31(5):713-716.杨海峰,侯朝桢.基于证据理论的小波萎缩影像去噪[J].光学技术,2005,31(5):713-716.

[19] LIN T-C.Fuzzy image restoration for noise reduction based on Dempster-Shafer theory[J].IEEE International Conference on Fuzzy Systems,2009,28(1):1931-1936.

[20] WANG L M,LEI L,ZOU H X.The fusion change detection of remote sensing images based on the D-Sevidential theory[J].Computer Engineering and Science,2011,33(7):50-54.王立民,雷琳,邹焕新.基于D-S证据理论的遥感影像融合变化检测方法[J].计算机工程与科学,2011,33(7):50-54.

[21] ZHU F X,DU Y F,XIA D C.Introduction to Artificial Intelligence[M].Wuhan:Wuhan University Press,2006:100-300.朱福喜,杜友福,夏定纯.人工智能引论[M].武汉:武汉大学出版社,2006:100-300.

[22] ZHANG M H.Study on WLAN based indoor location estimation technology[D].Shanghai:Shanghai Jiao Tong University,2009.张明华.基于WLAN的室内定位技术研究[D].上海:上海交通大学,2009.

Remote Sensing Image De-noising by Fusing Multiple Images Based on DS Evidence Theory

HUANG Dong-mei1,ZHU Gui-xian1,ZHANG Ming-hua1,WANG Li-lin2,SU Cheng2
(1.College of Information,Shanghai Ocean University,Shanghai 201306,China; 2.East China Sea Forecast Center Of SOA,People's Republic of China,Shanghai 200137,China)

The existing methods for de-noising a single remote sensing image tend to blur the image edges or give an imperfect de-noising result.To solve these problems,the de-noising method by fusing multiple remote sensing images based on DS evidence theory is proposed in this paper.The DS evidence theory is capable of utilizing multiple-source information and effectively dealing with cognitive uncertainty,and thus applicable to the cases of noise with uncertainty and randomness.Using the advantages of DS evidence theory,the paper aims to make full use of effective information of multiple remote sensing images taken by Landsat 8 in the sea-area around Shanghai.Four models are implemented to determine the probability of each pixel related with the noise,including the two-state Gaussian Mixture Model,edge analysis model, and two Noise Analysis Models based on spatial correlation.These four models work as the four evidences of DS theory to support the decision-making of de-noising scheme.Experimental results show that the method keeps the details of the image edge and texture information well while the noise is removed.

remote sensing image;DS evidence theory;image fusion;image de-nosing

July 28,2016

TP751

A

1671-6647(2017)03-0414-14

10.3969/j.issn.1671-6647.2017.03.011

2016-07-28

上海市科学技术委员会科研计划项目——地方院校能力建设(15590501900);极地海洋环境监测示范应用系统开发项目——极地海洋环境监测示范应用系统开发(201405031-05);国家自然科学基金项目——基于多模态深度学习的弱特征多源海洋遥感影像协同分类模型研究(41671431);国家自然科学基金青年基金项目——一种面向多模态遥感信息的质量抽样检验方案研究(41501419)

黄冬梅(1964-),女,河南郑州人,教授,博士生导师,主要从事海洋大数据管理、海洋GIS及辅助决策系统方面研究. E-mail:dmhuang@shou.edu.cn

*通讯作者:张明华(1977-),女,四川宣汉人,副教授,博士,主要从事海洋大数据管理方面研究.E-mail:mhzhang@shou.edu.cn