岛礁地形上拍岸浪的数值模拟研究

聂 屿,李训强*,朱首贤,张文静,汪 鸿

(1.国防科技大学气象海洋学院,江苏南京211101;2.河海大学海洋学院,江苏南京210098)

岛礁地形上拍岸浪的数值模拟研究

聂 屿1,李训强1*,朱首贤2,张文静1,汪 鸿1

(1.国防科技大学气象海洋学院,江苏南京211101;2.河海大学海洋学院,江苏南京210098)

近年来,越来越多的海岸工程与军事活动在岛礁上展开。研究岛礁地形上拍岸浪的传播特征具有重要的指导作用和现实意义。在对波浪破碎的研究中,数值模拟方法以其经济可行、操作性强的优势而得到了广泛的应用。本文采用基于完全非线性Boussinesq方程的数值模型FUNWAVE-TVD模式,对岛礁地形上拍岸浪的传播过程进行模拟,并将模拟结果与实验室数据进行对比。在此基础上,通过修改岛礁前坡坡度,分析了不同坡度下波浪的传播变化特征。结果表明,FUNWAVE-TVD模式能够较为准确地模拟岛礁地形上拍岸浪的非线性作用以及破碎现象。波浪破碎位置随岛礁前坡坡度的减小而前移。

Boussinesq方程;FUNWAVE模式;岛礁地形;拍岸浪

海浪是最为常见的海洋现象,通常分为风浪和涌浪。海浪由深水向近岸传播的过程中,由于水深变浅,加上海底地形、海中障碍物的相互作用,会发生折射、绕射、破碎和波能衰减等现象。当波浪向海岸拍击时,波高迅速增大后发生破碎,能量变化剧烈,这种波浪称为“拍岸浪”。拍岸浪对水工建筑、军事活动、港口和岛礁建设等都具有十分显著的影响。

近年来,越来越多的国家开始在岛礁上修建建筑物或在岛礁附近开展填海造岛工程。以南海为例,目前我国已经在南海岛礁附近实施了大规模的填海造岛行动。由于岛礁地形的复杂性,岛礁附近的波浪分布对填海造岛的顺利进行及其后期的维护保障影响很大。波浪在岛礁地形上的传播规律已成为近岸海动力学研究的重点。

研究近岸波浪破碎的方法主要包括现场观测、物理实验和数值模拟。其中,数值模拟方法以其经济可行、操作性强的优势而得到了广泛的应用。对于拍岸浪这种小尺度运动,常用的数值模型有缓坡方程模型、Navier-Stokes方程模型和Boussinesq方程模型。Boussinesq方程模型较好地描述了波浪的非线性特点,适用于岛礁等海底地形坡度非缓慢变化的情形,能够较好地模拟出波浪在传播过程中发生的反射、折射、绕射、破碎和衰减等现象。同时,为了提高Boussinesq方程的适用性,许多学者对模型的非线性与色散性进行了拓展与改进,使得模型得到了更加广泛的应用。

目前,国内外一些学者已经对岛礁地形上波浪的传播规律进行了研究。Kono和Tsukayama[1]将岛礁地形简化为陡坡,通过实验证明浅水处的(H/d)b值与Nelson实验结果一致。Young[2]在已有的波浪破碎与底摩擦理论基础上,通过分析实验数据,得到了波浪在珊瑚礁上传播的衰减率。梅弢和高峰[3]根据我国南海岛礁实测坡度进行实验,分析了波浪破碎指标。刘宁[4]通过实验分析了岛礁前坡坡度为1∶5条件下的波浪破碎指标、波高衰减公式以及频谱变化规律。刘思[5]利用基于Boussinesq方程的FUNWAVE-1D数值模型,对岛礁地形上规则波与不规则波的传播过程进行模拟,并对FUNWAVE-1D模式进行了改进,改进后模拟效果有了很大提高。李训强等[6]利用解放军理工大学海洋动力学实验室的风浪流水槽,自主设计了规则波在1∶30的缓坡地形下的传播实验,并采用基于完全非线性Boussinesq方程的FUNWAVE-TVD模式,对实验结果进行了数值模拟,基于模拟结果讨论了不同入射条件下的波浪传播特性。

(李 燕 编辑)

然而,由于受实验条件的限制,对于岛礁地形上波浪传播的实验研究和数值模拟,多数是分析单一地形条件下的波浪传播特征。关于坡度对波浪传播的影响,以及不同坡度下数值模拟的参数选择,讨论较少。

本文采用基于完全非线性Boussinesq方程的FUNWAVE-TVD模式,首先对解放军理工大学自主设计的坡度为1∶15的较陡坡度下的波浪传播实验进行模拟。然后,对柳淑学等[7]、Yao等[8]、Demirbil和Nwogu[9]等在不同坡度地形下的实验进行模拟。最后,采用控制变量法对数值地形进行修改,讨论了不同坡度对波浪传播的影响。

1 FUNWAVE-TVD模式简介

Funwave模式最初是由Kirby等[10]建立的完全非线性Boussinesq模型。在此基础上,Shi等[11]提出了FUNWAVE-TVD数值模式。该模式在理论与数值解法上都有较大的改进,主要包括:利用有限体积和有限差分相结合的方法对方程在空间上进行离散;采用基于三阶Runge-Kutta方法的自适性时间步长和MUSCL-TVD解法;对于波浪破碎的处理采用激波捕捉法;在计算中采取HLL构造方法等。改进后的模式能够更好地模拟波浪在浅水的传播、破碎、漫滩等过程,适用范围更加广泛。

1.1 控制方程

FUNWAVE-TVD模式的控制方程为

式中,M为水平体积通量;V1,V2和V3分别为Boussinesq方程中的色散项;R代表方程中的扩散项和耗散项。

1.2 数值解法

在FUNWAVE-TVD模式中,求解方程采用了有限体积与有限差分相结合的方法。同时,模式采用高阶MUSCL-TVD格式处理通量项。

对于方程积分的时间步长,模式采用三阶Runge-Kutta方法,保持了较好的稳定性。在CFL条件的限制下,时间步长可表示为

式中,C是柯朗数,在模式中C=0.5,Δt随着计算过程而不断调整。

1.3 波浪破碎

对于波浪破碎的处理采用了Tonelli和Petti[12]的方法。由于完全非线性浅水方程(NSWE)在TVD格式下能够模拟出水跃,因此,在FUNWAVE-TVD模式中,用波高与当地水深的比值是否超过一定的阈值来判断波浪破碎,即如果判断为破碎,则不再考虑Boussinesq方程中的高阶非线性项和色散项,将方程退化为NSWE。Tonelli和Petti[12]建议这个阈值λ取为0.8。

2 FUNWAVE-TVD模式对拍岸浪水槽实验的模拟检验

2.1 双斜坡地形下规则波传播的模拟检验

该实验为自主设计实验,在解放军理工大学海洋动力实验室的风浪流水槽中进行。实验设计如图1所示。地形由2个斜坡构成,其中较陡的斜坡坡度为1∶2.5,较平缓的斜坡坡度为1∶15。连接处的高度为0.225 m。斜坡用木板制成,以铁质框架固定,表面用2 cm厚的水泥平整。其中水深h1=0.60 m。整个传播区域布置若干个波高仪,实验中根据每次波浪的破碎位置进行适当的调整。

图1 水槽实验设计图Fig.1 Schematic diagram for configuration of physical experiment

本文利用FUNWAVE-TVD模式对上述实验进行模拟,网格间距为0.012 5 m,模拟时间为60 s。模式运行20 s以后,波面基本稳定,再计算波面稳定后的平均波高,与观测数据进行比较。图2为两种不同入射条件下,数值模拟与实验结果的对比。图2a的入射波高(H入射)为0.08 m,周期为1.0 s,破碎阈值λ取0.55。图2b的入射波高为0.07 m,周期为1.5 s,破碎阈值λ取0.50。由图可知,数值模拟与实验结果趋势一致。波浪在向斜坡传播的过程中,平均波高先保持不变,直至临近破碎位置迅速增大后发生破碎。

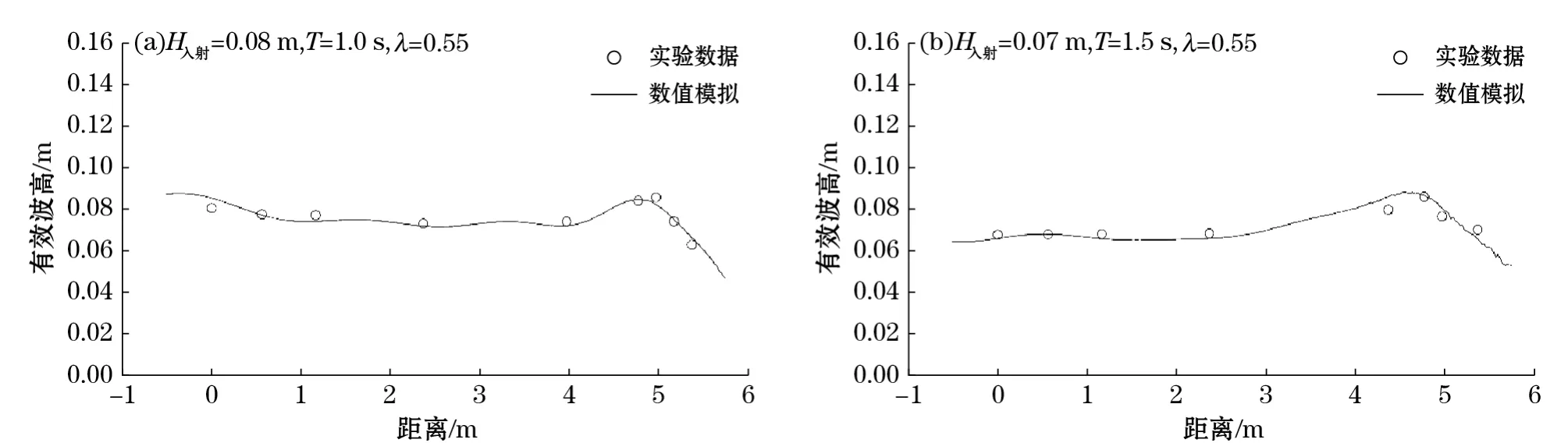
图2 实验数据与数值模拟的波高比较Fig.2 Comparison of wave height simulated by numerical and physical experiments

2.2 前坡坡度1∶5地形下不规则波传播的模拟检验

该实验为柳淑学等[7]在大连理工大学进行,实验设计如图3所示。其中,岛礁前坡坡度为1∶5,岛礁高度为0.50 m。造波机位于距离斜坡24 m处。沿程一共布置了18个波高仪,相对位置如图1所示。岛礁表面为混凝土光滑抹面。该实验分为3大组,坡前水深h1分别取为0.625,0.715和0.835 m,h2=h1-0.50(岛礁高度)。每组分别采用不同有效波高和有效周期的入射波进行测量。

图3 岛礁地形下波浪传播实验设计与布局(m)Fig.3 Configuration of the experiment for surf propagating onto reefs(m)

实验中采用的不规则海浪谱为工程上常用的合田改进的JONSWAP谱,谱型如式(4)～式(7)。式中, Hs为有效波高,Ts为有效周期,ωp为谱峰频率,σ为谱形参数,γ为峰升因子,取为3.3。

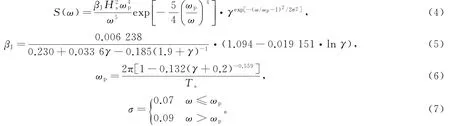
本文针对大连理工大学实验中的岛礁地形,利用FUNWAVE-TVD模式模拟了不同有效波高、有效周期的波浪传播过程。模拟结果如图4所示。图中0.2-1.3-6-0.33代表相对水深比h2/h1=0.2,有效周期Ts=1.3 s,有效波高Hs=0.06 m,破碎阈值λ=0.33。从图中可得,FUNWAVE-TVD模式较好地模拟了该地形下不同水深、有效波高和有效周期条件下不规则波的波高分布。为了定量分析计算结果的精确度,引入均方根误差RMSE、相关系数R和一致性指标A三个统计量。每组模拟结果与实验数据的统计量如表1所示。

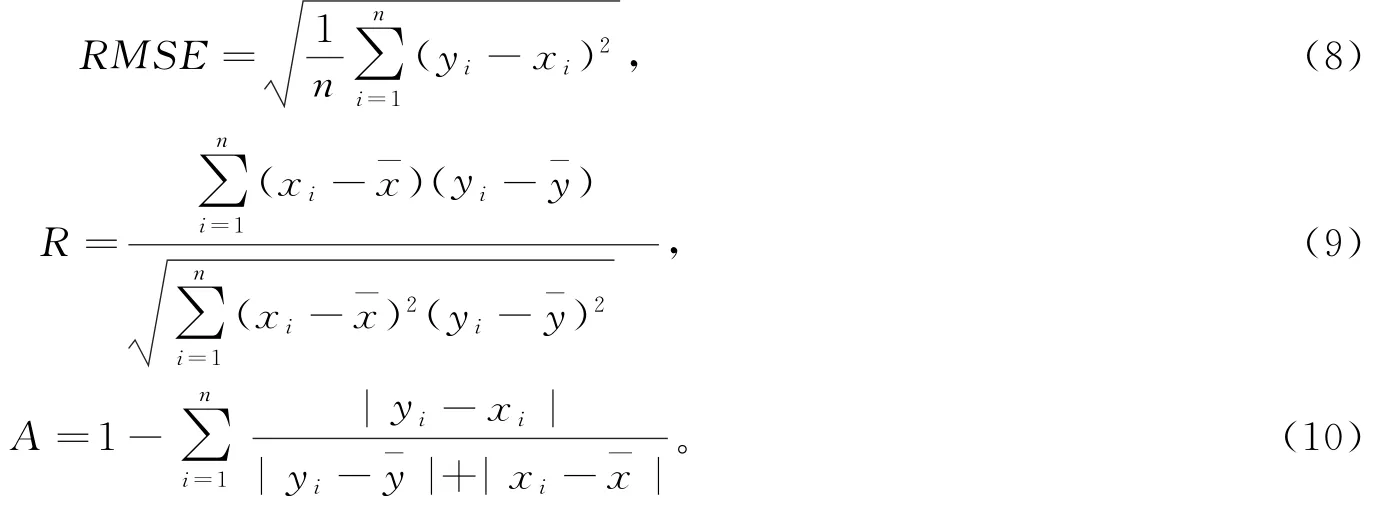
由图4可知,不规则波在向岛礁传播的过程中,波高先增大,然后迅速减小,发生破碎。当水深和入射波高一定时,周期越大,破碎波高越大。破碎可能发生在斜坡或礁盘。

图4 实验数据与数值模拟的波高比较Fig.4 Comparison of wave height simulated by numerical(round dots)and physical(square dots)experiments

表1 数值模拟结果统计量Table 1 Parameters and statistical results of experiments

2.3 前坡坡度1∶6地形下不规则波传播的模拟检验

该实验为Yao等[8]进行的波浪在岛礁地形下的传播特性研究。岛礁前坡坡度为1∶6,水平段距离为2 m。礁盘上的水深为0.05 m,水平长度为7 m。沿程布置了12个波高仪,相对于岛礁前沿的距离分别为-4.35,-4.25,-4.00,0.95,1.45,2.00,2.45,2.95, 3.65,5.25,6.95和8.75 m。不规则波的有效波高为0.087 m,谱峰周期为1.67 s。在数值模拟中,地形设置与实验完全相同,网格间距为0.05 m。模拟时间为90 s。破碎阈值λ取0.35。FUNWAVE-TVD模拟结果如图5所示。

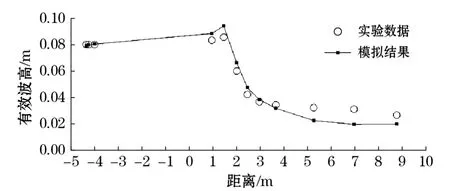
图5 实验数据与数值模拟的波高比较Fig.5 Comparison of wave height simulated by numerical and physical experiments

由图可知,FUNWAVE-TVD模式较好地模拟了该地形下不规则波的传播过程,计算波高与实验结果较为吻合。通过计算可知,模拟结果与实验数据的均方根误差RMSE=0.006 1 m,相关系数R=0.99,一致性指标A=0.90。在陡变地形的作用下,不规则波的波高先增大,后迅速减小,最后趋于稳定。波浪破碎发生在岛礁斜坡上。

2.4 多斜坡地形下不规则波传播的模拟检验

Demirbil和Nwogu[9]设计了一个复杂地形下的不规则波的传播实验。实验设计如图6所示。该地形由3个斜坡共同组成,平均坡度为1∶12。岛礁高度为0.50 m。总水深为0.531 m,则礁盘上水深为0.031 m。沿程布置了9个波高仪,相对于岛礁前沿的距离分别为-1.11,-0.92,-0.59,2.75,3.68,4.22, 4.80,6.97和9.15 m。不规则波的有效波高为0.075 m,谱峰周期为1.5 s,破碎阈值λ取0.45。模拟结果如图7所示。

图6 实验设计示意图Fig.6 Schematic diagram for the experiment

图7 Demirbil和Nwogu[9]实验数据与数值模拟的波高比较Fig.7 The simulated wave height versus Demirbil and Nwogu[9]experiment data

由图7可知,不规则波在传播过程中,有效波高先略有增大,然后发生破碎,波高迅速减小,最后波浪趋于稳定。波浪破碎发生在斜坡上。模式计算结果与实验数据趋势一致。

3 不同地形下拍岸浪传播特性的分析

上述研究表明,FUNWAVE-TVD模式模拟规则波和不规则波在陡坡上传播的效果较好,不同坡度的地形下模拟结果均与实验数据保持了较高的一致性。不同地形下,破碎阈值的选取差别较大。总体而言,坡度越缓,选择的破碎阈值越大。为进一步研究不同坡度条件下不规则波的传播特性,现利用FUNWAVETVD模式,采用控制变量法,对不规则波的传播特征进行对比分析。

数值模式设置与图3相同,水深为0.625 m,入射波的有效波高为0.06 m,有效周期为2.0 s。其中,岛礁前坡坡度分别为1∶4,1∶5,1∶6,1∶7,1∶8,1∶10六种情况,网格间距为0.05 m,模拟时间为90 s。破碎阈值取该坡度下前文的4组实验的平均值0.34。计算时,将礁盘边缘的位置固定,不同坡度的地形从不同位置开始。模拟结果如图8所示,图中斜坡起始的位置与曲线起始的位置相同。

图中地形坡度从左至右依次减小。数值计算结果表明,波浪破碎基本发生在礁盘边缘附近,而破碎位置随坡度的减小向前移,破碎波高随地形坡度的变缓而略有减小。

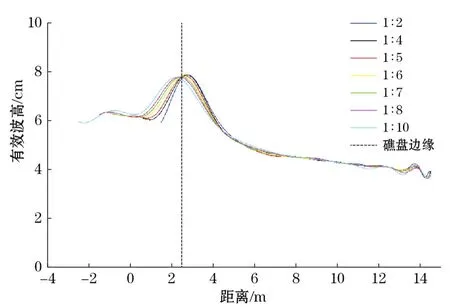
图8 数值模拟不同坡度下不规则波的波高比较Fig.8 Comparison of simulated surf heights by experiments with different slopes

4 结 论

本文主要应用基于Boussinesq方程的FUNWAVE-TVD模式,对岛礁地形上规则波和不规则波的传播过程进行数值模拟,并将模拟结果与实验数据进行对比分析。结果表明,FUNWAVE-TVD模式能够较好地模拟规则波和不规则波在陡变地形下的沿程波高分布,波高呈现出先增大后发生破碎并迅速减小的特征。不同坡度下不规则波的模拟结果与实验数据趋势一致。同时,通过数值模拟,发现在只调整岛礁前坡坡度的情况下,波浪破碎位置随坡度的减小而前移,而破碎波高和破碎后波形稳定后的波高在现有入射条件下随坡度变化很小。

在数值模拟中也发现以下问题:1)对于不同坡度地形的数值模拟,选取的判断波浪破碎的阈值不同,在对自主实验的规则波进行模拟时,λ取为0.55效果较好;而在地形更为陡峭的1∶5坡度下的不规则波的数值模拟中,λ取值为0.30～0.37;2)不同入射条件下,λ取值会有不同,相同入射条件而不同坡度地形下,λ取值也不同;3)在不同入射波高和入射周期条件下,破碎波高的大小可能随坡度减小而呈现出不同的变化。下一步将结合实验与数值模拟,分析研究λ取值与入射波高、周期、水深和地形坡度的关系,为拍岸浪的数值预报提供参考。

[1] KONO T,TSUKAYAMA S.Wave transformation on reef and some consideration on its application to field[J].Costal Engineering in Japan,1980,23:45-57.

[2] YOUNG I R.Wave transformation over coral reefs[J].Journal of Geophysical Research Oceans,1989,94(C7):9779-9789.

[3] MEI T,GAO F.Flume experiment research on law of wave propagation in reef flat[J].Journal of Waterway and Harbor,2013,34(1): 13-18.梅弢,高峰.波浪在珊瑚礁坪上传播的水槽试验研究[J].水道港口,2013,34(1):13-18.

[4] LIU N.Experimental research on wave propagation characteristics under reef terrain[D].Dalian:Dalian University of Technology,2014.刘宁.波浪在岛礁地形上传播特性的试验研究[D].大连:大连理工大学,2014.

[5] LIU S.The numerical simulation of wave propagation on the reefs terrain by the numerical model based on Boussinesq equations[D]. Dalian:Dalian University of Technology,2015.刘思.基于Boussinesq方程数值模型对岛礁地形上波浪传播的模拟[D].大连:大连理工大学,2015.

[6] LI X Q,YANG J X,ZHU S X,et al.Numerical simulation of surfing waves on mild slopes[J].Advances in Marine Science,2015,33 (2):155-163.李训强,杨家轩,朱首贤,等.缓坡地形拍岸浪数值模拟研究[J].海洋科学进展,2015,33(2):155-163.

[7] LIU S X,LIU N,LI J X,et al.Experimental researches on wave propagation characteristics on reefs terrain[J].The Ocean Engineering,2015,33(2):42-49.柳淑学,刘宁,李金宣,等.波浪在珊瑚礁地形上破碎特性试验研究[J].海洋工程,2015,33(2):42-49.

[8] YAO Y,HUANG Z,MONISMITH S G,et al.1DH Boussinesq modeling of wave transformation over fringing reefs[J].Ocean Engineering,2012,47(2):30-42.

[9] NWOGU O,DEMIRBILEK Z.Infragravity wave motions and runup over shallow fringing reefs[J].Journal of Waterway Port Coastal& Ocean Engineering,2010,136(6):295-305.

[10] KIRBY J T,WEI G,CHEN Q,et al.FUNWAVE 1.0,Fully nonlinear Boussinesq wave model.documentation and users manual[C]∥KIRBY J T.Center for Applied Coastal Research.Delaware:University of Delaware,1998.

[11] SHI F Y,KIRBY J T,TEHRANIRAD B.Funwave-tvd-1.0 manual[M].New York:University of Delaware,2011.

[12] TONELLI M,PETTI M.Simulation of wave breaking over complex bathymetries by a Boussinesq model[J].Journal of Hydraulic Research,2011,49(4):473-486.

[13] YAO Y,DU R C,YUAN W C,et al.Experimental study of wave transformation around the surf zone over fringing reefs[J].Haiyang Xuebao,2015,37(12):66-73.姚宇,杜睿超,袁万成,等.珊瑚岸礁破碎带附近波浪演化实验研究[J].海洋学报,2015,37(12): 66-73.

Numerical Simulation of Surf Shoaling and Breaking on Reefs

NIE Yu1,LI Xun-qiang1,ZHU Shou-xian2,ZHANG Wen-jing1,WANG Hong1
(1.College of Meteorology and Oceanography,National University of Defense Technology,Nanjing 211101,China; 2.College of Oceanography,Hohai University,Nanjing 210098,China)

In recent years,more and more offshore constructions and military operations are conducted on reefs,and thus the research on propagation characteristics of surf on reefs terrain has become more and more important.In this study,FUNWAVE-TVD model based on fully nonlinear Boussinesq equations are used to simulate the processes of wave propagation on the reefs.Comparison between the numerical simulation and physical experiment shows that the FUNWAVE-TVD model is suitable for simulating the wave nonlinear effects and breaking on reefs.The location of wave breaking retreats as the slope of reefs decreases.

Boussinesq equation;FUNWAVE-TVD model;reefs terrain;surf

July 4,2016

P731

A

1671-6647(2017)03-0329-08

10.3969/j.issn.1671-6647.2017.03.003