二层海洋赤道Kelvin波解析解模态分析
2017-08-12路凯程
卢 姁,路凯程,张 铭
(1.解放军61741部队,北京100094; 2.解放军理工大学气象海洋学院大气环流与短期气候预测实验室,江苏南京211101)
二层海洋赤道Kelvin波解析解模态分析
卢 姁1,2,路凯程1,2,张 铭2
(1.解放军61741部队,北京100094; 2.解放军理工大学气象海洋学院大气环流与短期气候预测实验室,江苏南京211101)
采用赤道β平面近似下的线性化二层海洋扰动方程组,对其中的赤道Kelvin波做解析求解,结果表明:该赤道Kelvin波共有2个模态;两者上、下层流场均为东向纬向流,振幅均在赤道处最大,并都呈经向衰减态势,两者波动均是非频散的,这些都与经典Kelvin波相同。第一模态(前者)的相速要比第二模态(后者)大2个量级,后者相速与海洋流速相近。前者是快波模态,后者是慢波模态。前者周期约为半天,后者约为1季度,并具气候意义。前、后者各层流场向高纬的衰减分别表现为缓慢和迅速,后者呈赤道俘获波形态。两模态各层位势场向高纬的衰减同流场。将后者与实际热带印度洋和太平洋的实况及诊断作对比后知,它们具有一致之处。后者能对实际赤道海洋情况以及ENSO现象做出某种解释。
二层海洋模型;赤道Kelvin波;模态分析;解析解;次表层
赤道海洋Kelvin波因其与太平洋ENSO和印度洋偶极子(IOD)密切有关,一直倍受学者的重视[1-3]。厄尔尼诺是发生在热带中东太平洋海温异常增暖的气候现象,也是全球气候变化中最重要和最强的信号。厄尔尼诺虽发生在热带太平洋地区,但对全球气候的短期变化有重要影响。次表层暖水的快速东传,会使热带中东太平洋海表温度明显增暖,促使厄尔尼诺事件爆发,而暖水的东传是因为海洋赤道Kelvin波造成的[4]。于飞等[5]采用次表层海温异常的资料,分析了太平洋北赤道逆流的年际变化特征及其与ENSO循环的联系;该研究结果验证了在北赤道逆流的年际变化中海表面风应力场是关键因素,而海洋赤道Kelvin波和Rossby波以及洋流本身是海洋内部的主要动力调整机制。Mosquera等[6]研究了中太平洋季节内海洋赤道Kelvin波与ENSO的关系,发现在中太平洋厄尔尼诺事件中,该海洋赤道Kelvin波的活动在澳大利亚夏季有季节内增强。曹国娇[7]做了印度尼西亚贯穿流及周边海域海洋季节内变化的研究,结果表明,由赤道印度洋纬向风异常所激发的季节内海洋赤道Kelvin波向东传播,在印度洋东边界反射成为海洋沿岸Kelvin波,沿苏门答腊-爪哇岛岛链西南沿岸继续向东传播并进入印尼海,最远可以抵达望加锡海峡和翁拜海峡。张东凌等[8]和卢姁等[9]分别对热带印度洋和热带太平洋的流场异常做了复EOF分解,发现该两热带大洋都有这样的现象:流场异常表现为纬向流的形态,其向赤道南北两侧迅速衰减,表现为赤道俘获波的形态,而这与海洋赤道Kelvin波相类似。
近年来,在有关ENSO的研究中,热带太平洋次表层海温异常的研究形成了一个热点[10-12]。黎鑫和李崇银[12]对比了东太平洋型厄尔尼诺和中太平洋型厄尔尼诺的生消演变与赤道太平洋次表层海温异常的关系;结果表明:两类厄尔尼诺与赤道西太平洋次表层海温异常都有明显负相关,其发生与赤道温跃层结构的变化密切有关,其生消过程中,赤道次表层海温异常的传播、演变都起到重要作用;两类厄尔尼诺事件中,次表层海温异常的传播有明显不同的路径,东太平洋型主要的传播回路在赤道及其北侧,而中太平洋型则在赤道及其南侧。陈永利等[13]研究了赤道太平洋次表层海温异常年际和年代际变率的演化特征,并讨论了其与ENSO循环的关系;指出赤道太平洋次表层海温异常与ENSO类似,都以赤道西太平洋暖池与赤道东太平洋这两者海温异常中心的明显反相变化为主要特征,并通过赤道西太平洋暖池次表层海温异常中心沿温跃层向东向上传播来实现;赤道西太平洋暖池次表层海温异常的年际变率决定了ENSO循环。李锋[14]探讨了东亚夏季风年际变化特征及其与热带太平洋次表层海温异常的关系,指出热带太平洋次表层海温EOF第一模态是ENSO循环在次表层的体现,热带太平洋次表层海温异常与东亚夏季风指数有很好的超前相关,前期西太平洋暖池次表层海温异常向东传播所导致的类ENSO事件衰减,其是次年夏季风强弱的显著信号;当前期秋冬季节西太平洋暖池次表层海温异常偏暖(冷)并有明显向东传播趋势时,它将使赤道中东太平洋冷(暖)海温变暖(冷),而当年东亚夏季风偏强(弱)。
(王 燕 编辑)
以上有关ENSO的研究都提到了热带太平洋有次表层海温异常的东传现象,其会引起气候异常,并与ENSO循环有关;而该次表层海温异常东传现象大多认为与海洋赤道Kelvin波有联系。故而海洋赤道Kelvin波在海洋次表层的表现和特点理应受到关注和重视。解析研究能直接给出各物理量之间的定量联系,并得到各物理规律的数学表达式,这是诊断分析和数值实验难以做到的。对于浅水(正压)赤道Kelvin波,Matsuno[15]做了开创性的工作,求出了线性化下的解析解,下文为方便称其为经典Kelvin波。然而在分层海洋中能否求出海洋赤道Kelvin波的解析解?此解析解各模态的特点和性质如何?此解各模态在实际海洋特别是在次表层有何表现?这些都是涉及物理海洋学的理论问题,也与ENSO等气候异常密切有关。国内外对以上问题至今鲜有具体答案。最简单的分层海洋是二层海洋,其已能概括表层和次表层的情况。为此本文采用二层海洋模型,对该模型中的二层海洋赤道Kelvin波做了解析求解,得到了该解析解的2个模态,并讨论了其特点和性质,还与大洋实况做了比较和讨论。就此而言,本文工作具有创新性。
1 数学模型和求解
采用赤道β平面近似下的线性化二层海洋模型,这里不考虑基本流以及外强迫和摩擦,仅考虑自由波动模态,其控制方程组为[16]
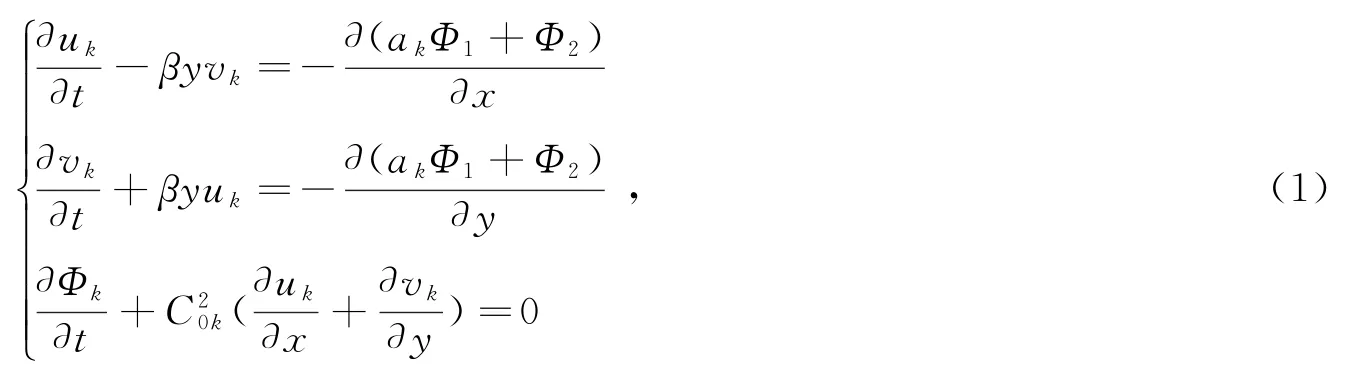
式中,k=1,2,其分别为上、下两层编号;uk,vk和Φk分别代表海洋上、下二层流场和位势场的扰动(异常),为简便,后文中略去“扰动”或“异常”的称谓。这里分别为上、下二层流体静止时的厚度,其分别为常数,也分别为常数;a1=1,a2=ρ1/ρ2<1,后者为上、下二层密度之比,也是大于0的常数。
对经典Kelvin波有v≡0,且此时求解析解也较方便[16];受此启发,现本文试求方程组(1)中vk≡0的波动特解;此特解中最简单的形式是:在上、下二层x方向的波长均相同,即波数都为m,频率也均相同,都为σ,且上、下二层无位相差;而在实际海洋中,表层、次表层中的波动也常呈现这种情况[13];为此则可设

注意到vk≡0后,将式(2)代入式(1)后则有
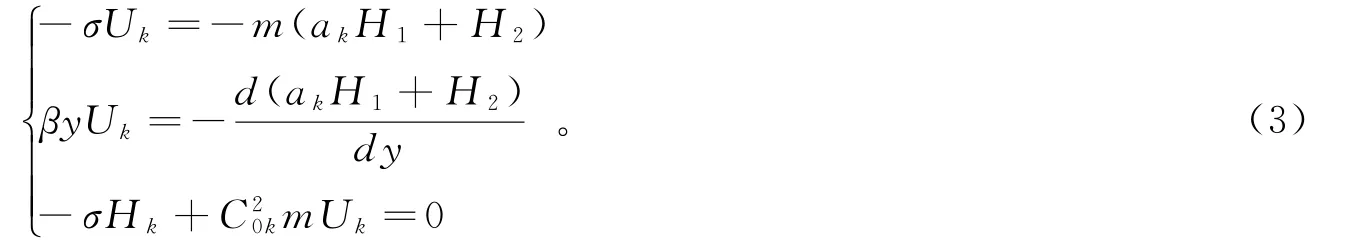
为解析求出上述特解,再设


由式(5)第一和第二式可求得:

式(6)中两式必须相容,故有m/σ=2δ/β,由此可求得

式中,c=σ/m为相速。由式(7)知,一旦该特解的波数和频率确定后,则经向衰减参数就确定了,即随纬度增加而衰减的程度也就确定了。


上式若有非零解,必须系数行列式为0,即有
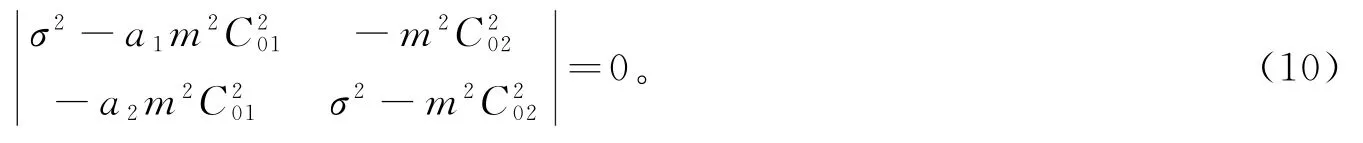
由式(10)可得

求解方程(11)得:

将式(12)开方,这样σ可有“+”“―”两个符号,因δ≥0,则由式(7)知应有σ≥0,故这里σ前取“+”号。此时所求的波动特解向东传播,且随纬度增加会呈指数平方衰减,并有:

上式根式中的根式前有“±”号,代表此时该波动特解有两个模态,现定义取“+”号的为第一模态,取“―”号的为第二模态。而波动的相速则为
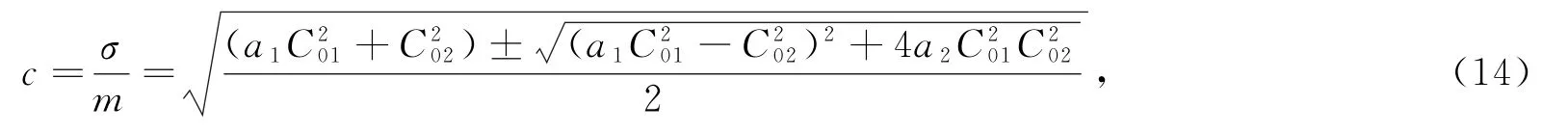
注意到式(14)中的c与波数或波长无关,这表明该波动特解是非频散的。
在海洋中有a1=1,a2=ρ1/ρ2=1-ε<1,ε≪1为一个很小的无量纲正数。将该a1,a2值代入式(13)可得上述两模态的频率σ,其为
式(15)中大括号上、下两式分别是第一、二模态的频率表达式,相应相速则为

求得参数σ,δ,c的值后,再通过式(4)、式(2)和式(8),就可得到此二层海洋模型中该波动特解的解析表达式:

2 结果分析
2.1 第一模态
图1给出了本文Kelvin波第一模态上、下层的纬向流场和位势场的经向振幅。在赤道处两者上层的值分别为10 cm·s-1和1.81 m2·s-2,下层则分别为8 cm·s-1和2.89 m2·s-2。上、下层纬向流场赤道处的振幅值是事先设定的,上层的值要略大于下层;然而计算结果表明,下层位势场赤道上的振幅值则要明显大于上层,即位势场扰动在次表层表现得更明显;这是因式(17)中明显大于的缘故。由图1可见,上、下层纬向流场和位势场的振幅最大值都出现在赤道上,并随纬度增加而衰减,但衰减很慢;例如上层纬向流场的振幅在赤道上为10 cm·s-1,在距赤道500 km处衰减为约9.5 cm·s-1,仅衰减了约0.5 cm·s-1;下层流场和上、下层位势场也都同样衰减很慢。

图1 第1模态流场和位势场振幅的经向分布Fig.1 Meridional distribution of the amplitude of flow field and potential field of the first mode
图2 给出了以赤道为中心,南北各取500 km算得的本文Kelvin波第一模态的上层流场,该流场呈纬向流。t=0时(图2a),因该Kelvin波波长为2 000 km,故其在0~500 km有东向流;在500~1 500 km则有西向流;在1 500~2 500 km又有东向流。该东、西向流的极值都出现在赤道上,为10 cm·s-1(图1a)。综上所述表明该流场随纬度增加而衰减得很慢。当t=T/4时(图2b,T是周期,该模态为0.427 d,非常短),则该Kelvin波也在快速东传,东向流与西向流的交界已东移至1 000 km处,其他均与图2a类似。当t=T/2时(图2c),该流场继续快速东传,此时该流场与t=0时的流场恰好反位相。当t=3T/4时(图2d),该流场仍快速有规律东传,并与t=T/4时的流场也呈反位相。当经过1个周期T即0.427 d后,该Kelvin波的流场形态又回到t=0时(图2a)的状态,完成了周期为0.427 d的循环。该Kelvin波下层流场的水平分布类似图2,仅每个图中的比例尺标注由图2中的10更改为8,其单位也为cm·s-1,为此该图不再给出。
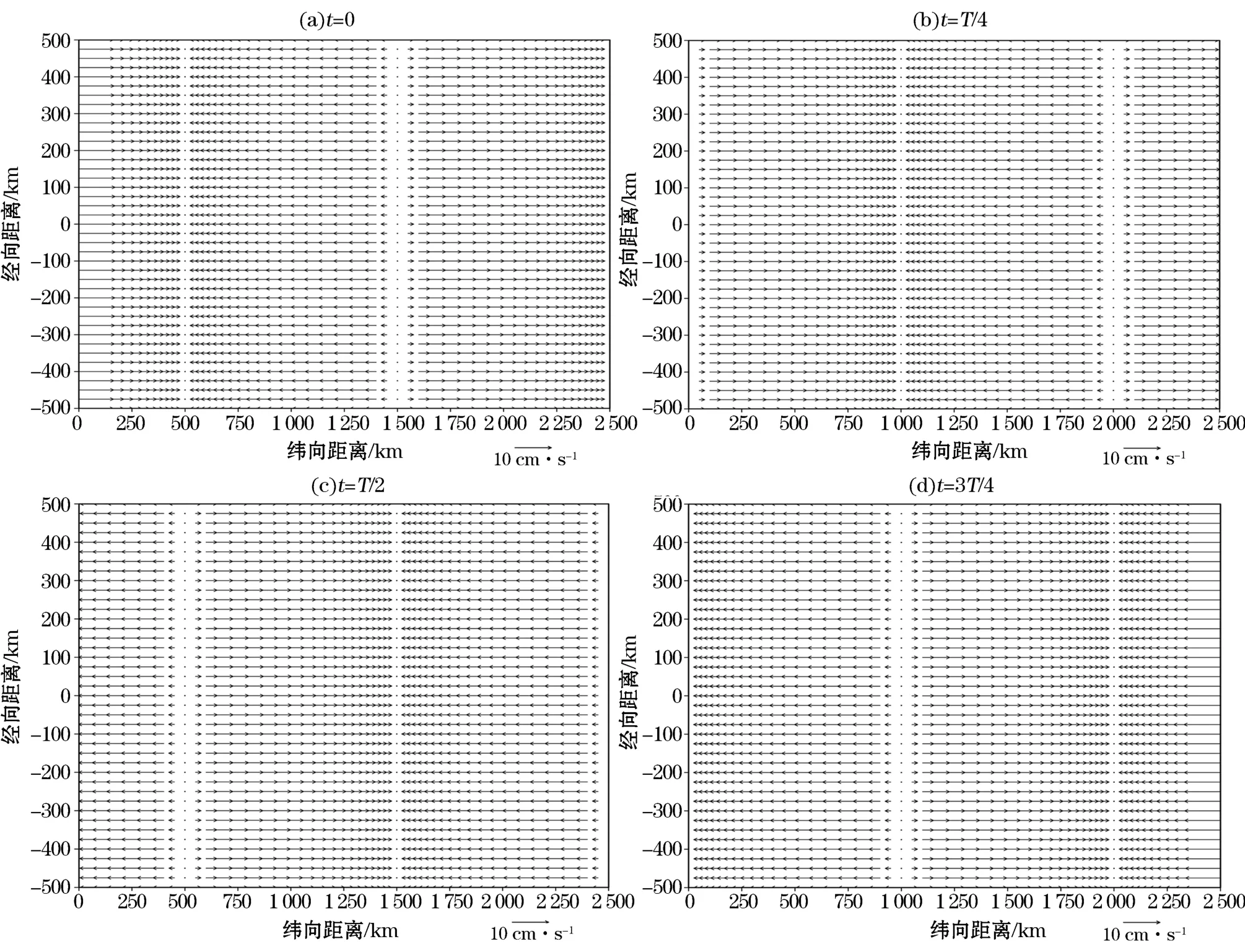
图2 第一模态各时刻t上层流场的水平分布Fig.2 Horizontal distribution of the upper flow field of the first mode at different time setps
图3 给出了赤道上x=0处本文Kelvin波第一模态上层流场和位势场随时间的变化。赤道上该流场和位势场的振幅分别为10 cm·s-1和1.81 m2·s-2,两者随时间都呈余弦函数振荡,且呈现同位相变化。对于下层流场和位势场,其赤道上两者随时间的变化类似于图3,仅赤道上两者振幅分别为8 cm·s-1和2.89 m2·s-2,其他情况都与上层相同,为此相应的图也略。下层位势场的该振幅要较上层大,原因在上文已述。

图3 第一模态赤道上x=0处上层流场和位势场随时间的变化Fig.3 Variation of the upper flow field and potential field of the first mode at x=0
2.2 第二模态
图4给出了本文Kelvin波第二模态上、下层的纬向流场和位势场在各经度上的振幅。在赤道其上层的值分别为10 cm·s-1和383.5 m2·s-2,下层则为8 cm·s-1和613.6 m2·s-2。这里位势场扰动要远大于第一模态,且在次表层表现得更明显。由图4可见,上、下层纬向流场和位势场的振幅最大值也都出现在赤道上,并也随纬度增加而衰减,但与第一模态不同的是:其都衰减得非常快,例如上层流场的振幅在赤道上为10 cm·s-1,在距赤道300 km处就衰减到约为0了;下层流场和上、下层位势场也都如此。
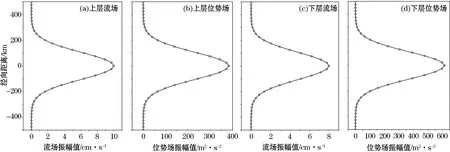
图4 第二模态流场和位势场振幅的经向分布Fig.4 Meridional distribution of the amplitude of flow field and potential field of the second mode
图5 给出了与图2范围相同的本文Kelvin波第二模态的上层流场。t=0时(图5a),此时同样在0~500 km有东向流;在500~1 500 km则有西向流;在1 500~2 500 km又有东向流。该东、西向流的极值也都出现在赤道上,为10 cm·s-1(图4a)。该流场随纬度增加衰减得非常快,在距赤道200 km外,流场已很微弱,即该流场被赤道俘获在2°S~2°N的范围内,呈现赤道俘获波的形态。当t=T/4时(图5b,T是周期,该模态为90.6 d,其比第一模态要大2个量级),此时相应于该Kelvin波的东传,东向流与西向流的交界也东移至1 000 km处,其他均与图5a类似。与第一模态不同的是:第二模态东传相速为0.256 m·s-1,远较第一模态的54.22 m·s-1要小,故其东传也远较第一模态要慢很多。当t=T/2时(图5c),该流场继续东传,此时该流场与t=0时的流场恰好反位相。当t=3T/4时(图5d),该流场仍有规律东传,其与t=T/4时的流场也呈反位相。经过1个周期T(即90.6 d)后,该Kelvin波的流场形态又回到t=0时(图5a)的状态,完成了周期为90.6 d的循环。该Kelvin波下层流场的水平分布与图5类似,仅每个图中的比例尺标注由图5中的10更改为8,其单位也为cm·s-1,为此该图也不再给出。

图5 第二模态各时刻t上层流场的水平分布Fig.5 Horizontal distribution of the upper flow field of the second mode at different time steps
图6 给出了t=0时本文Kelvin波上、下层的纬向流场和位势场两者的水平分布,图的范围同图5。上层两者绝对值的最大都出现在赤道上,随着纬度增加则该值迅速衰减。两者之间无位相差,且有东向流场对应于正位势,反之亦然(见图6a和6b),这也是经典Kelvin波两者的配置特点[15,19]。在其他时次,两者与图5相应,均有规律东传,90.6 d后完成一个周期循环。下层的情况与上层类似,下层位势场扰动在赤道上的绝对值约为上层该值的1倍(见图6c和6d)。
图7给出了赤道上x=0处本文Kelvin波第二模态上层流场和位势场随时间的变化。赤道上该流场和位势场的振幅分别为10 cm·s-1和383.5 m2·s-2,在此该位势场的振幅较第一模态的1.81 m2·s-2要大2个量级,两者随时间都呈余弦函数振荡,且呈现同位相变化,但其振荡远较第一模态要慢。对于下层流场和位势场,其类似图7,仅赤道上两者振幅分别为8 cm·s-1和613.6 m2·s-2,其他情况都与上层相同,为此相应的图也略。下层位势场扰动的该振幅也较上层要大。

图6 第二模态t=0时刻各层流场和位势场的水平分布Fig.6 Horizontal distribution of the flow field and potential field of each layer of the second mode at t=0

图7 第二模态赤道上x=0处上层流场和位势场随时间的变化Fig.7 Variation of the upper flow field and potential field over time of the second mode at x=0
3 讨 论
3.1 两模态的异同
第一、二模态的相同之处在于:两者的流场均为纬向流,无经向流,均向东传播,两者的振幅均在赤道上最大,都随着纬度增加而衰减。两者在流场与位势场的配置上无位相差,均同经典Kelvin波的配置,即东向流对应于正位势,反之亦然。两者均有下层位势场的扰动要大于上层的特征。两者波动均是非频散的,其相速与波长无关,这也是经典Kelvin波的特点。
两者的不同则在于:第一模态上、下层的流场(纬向流场)向高纬衰减缓慢,在赤道上和在距赤道南北500 km处两者流速最大仅相差约0.5 cm·s-1;第二模态上、下层流场则衰减迅速,到300 km处则已接近于0;第二模态上、下层的流场被赤道俘获在2°S~2°N,呈现赤道俘获波的形态。对于两模态上、下层位势场向高纬的衰减情况则与流场相同。第二模态位势场的扰动较第一模态要大2个量级,其在次表层表现突出。第一模态的传播相速为54.2 m·s-1,其比第二模态的相速(0.256 m·s-1)要大2个量级,第二模态的相速与海洋流速的量级相同,故其为慢波,而第一模态则为快波。为此可称第一模态为快波模态,第二模态为慢波模态。与此相应,第一模态的周期非常短,为0.427 d,即约半天,而第二模态的周期则要长得多,为90.6 d,即约1季度。
3.2 两模态在不同大洋的传播
对不同赤道大洋的长度l,以下对本文Kelvin波两模态的传播进行讨论。该Kelvin波由赤道大洋西岸传播到东岸的时间为τ=l/c,可见,赤道大洋长度l越长,则该Kelvin波从大洋西岸传到东岸所需的时间τ也越长。
赤道太平洋东西相距约160个经度,约17 600 km,将该Kelvin波第一、二模态的相速分别代入公式τ= l/c,可得该一、二模态由赤道大洋的西岸传到东岸所需的时间,其分别为3.76 d,797.1 d≈2.2 a。以上结果表明,第一模态(快波模态)因其传播太快而不具有气候意义,以下不再对该模态做讨论。而第二模态(慢波模态)则明显具有气候意义[20]。第二模态由赤道太平洋的西岸传到东岸所需的时间为2.2 a,这约为ENSO循环的半周期(ENSO年际变化周期为3~7 a),由此可见,ENSO应与该Kelvin波第二模态密切有关。
赤道印度洋东西相距约70个经度,约7 700 km。该Kelvin波的第一、二模态由赤道印度洋的西岸传到东岸所需的时间分别为1.64 d,348.7 d≈1.0 a,而后者与IOD的半周期相近(IOD年际变化周期为2~4 a),故IOD也应与该Kelvin波的第二模态有密切关系。
赤道大西洋东西相距约45个经度,约4 950 km,并可得该Kelvin波第一、二模态由赤道大西洋的西岸传到东岸所需的时间分别为1.06 d,224.2 d≈0.61 a。由上文知,无论是赤道太平洋还是赤道印度洋,该Kelvin波第二模态从大洋西岸传播到大洋东岸的时间都在大洋异常年际变化周期的一半之内,由此可推断赤道大西洋应有一个周期1~2 a的大洋异常年际变化。Houghton等[21]通过船舶海温资料的主分量分析得到,其第一主分量最大值出现在赤道上,具有准2 a的年际变化,而这与本文该Kelvin波第二模态所得结果也相一致。
3.3 与实际大洋的比较
在此对该海洋赤道Kelvin波第二模态与实际大洋情况进行比较。宣莉莉等[22]给出了热带东印度洋各季节的表层环流。在5月份,赤道东印度洋在2°S~2°N出现一支流速较大的东向急流,最大流速有0.7 m·s-1,这就是Wyrtki急流(见文献[22]的图3)。本文Kelvin波第二模态上、下层东向流的形态均与此Wyrtki急流类似,两者都出现在约2°S~2°N之间,均为赤道所俘获,且流速较大都呈急流形态。故而此Wyrtki急流与该Kelvin波第二模态应该有关,换句话说,该Kelvin波第二模态在某种程度上能对此Wyrtki急流加以解释。
张东凌等[8]对10月热带印度洋上层大洋流场做了复EOF分解。其第一模态空间场上,海洋表层流动都被限制在3°S~3°N之内,赤道印度洋有一支窄而强的东向急流异常,呈赤道俘获形态,该急流表现类似Wyrtki急流(见文献[8]图1)。该复EOF分解第一模态时间系数年际变化具有2~4 a的周期,并反映了第一类IOD的综合特性,而这与3.2中有关赤道印度洋的内容相一致。该Kelvin波第二模态也能对以上结果加以解释。
卢姁等[9]对5月热带太平洋上层大洋流场也做了复EOF分解。在该复EOF分解第一模态(梅雨丰欠异常模态)空间场上,大洋上层明显流动也都被限制在5°S~5°N之内,该流场为赤道所俘获。表层和次表层在赤道及附近均呈纬向急流形态(见文献[9]图1)。该分解第一模态时间系数年际变化具有3~5 a的周期。在该复EOF分解第二模态(ENSO模态)空间场上,大洋上层明显流动也均在5°S~5°N,即流动也为赤道所俘获。然而与第一模态不同的是,第二模态表层和次表层在赤道及附近的流场流动方向不再具有一致性,第二模态表层在150°W以西,为西向流,在130°W以东则为东向流。第二模态时间系数年际变化具有ENSO的年际变化周期。该复EOF分解第一、二模态的特征也与本文3.2节中有关赤道太平洋的内容相一致。该Kelvin波第二模态也能对以上结果做出某些解释。
3.4 与ENSO的关系
近年来对ENSO研究中,热带太平洋次表层海温异常已是一个热点。有些学者[1-4]认为,热带太平洋次表层海温异常的东传会引起ENSO;而该异常东传则与海洋赤道Kelvin波有关。在本文的海洋模型中,虽未引进海温异常,但上、下层位势扰动异常值在某种意义上与海温异常成正比;其正扰动值越大,意味着海温正异常越大,反之亦然。注意到本文海洋赤道Kelvin波第二模态的最大位势扰动绝对值要远大于第一模态,这就意味着海温异常在具有气候意义的第二模态中表现更为突出。因次表层位势扰动是表层的近1倍,故次表层海温异常要较表层更加明显,且更引人关注。以上事实是对在ENSO研究中重视次表层海温异常的有力支持;也证实了次表层海温的东传是海洋赤道Kelvin波慢波模态东传的结果(见图6);在3.2中还指出,该Kelvin波第二模态从赤道太平洋的西岸传到东岸所需的时间约为ENSO循环的半周期;而上述这些都体现了该Kelvin波第二模态次表层位势扰动的特点,且确实表明ENSO现象与海洋赤道Kelvin波慢波模态有着密不可分的联系,后者异常会造成前者异常,从而导致气候异常。
4 结 论
采用赤道β平面近似下的线性化二层流体扰动方程组,解析求得了此方程组中仅有纬向流场的最简单特解;该特解具有经典Kelvin波的某些特点,其为二层海洋赤道Kelvin波。本文中还将该Kelvin波与赤道太平洋、印度洋的实况和诊断做了比较和讨论。在本文所取的典型参数下,可得以下结果:
1)该赤道Kelvin波共有两个模态;两者上、下层均仅有纬向流场,无经向流场,并均向东传播,波振幅均在赤道最大,并向高纬呈指数平方衰减态势,两者波动均是非频散的,这些均同经典Kelvin波。
2)该波第一模态的相速要比第二模态大2个量级,后者相速与海洋流速相近,故可称前者为快波模态,后者为慢波模态,前者周期约为半天,后者约为1季度,后者具气候意义。
3)该波第一、二模态各层流场向高纬衰减分别表现为缓慢和迅速,第二模态各流场被赤道俘获于2°S~2°N之间,呈赤道俘获波形态;两模态各层位势场向高纬的衰减情况同流场。
4)该波第二模态位势场扰动较第一模态要大2个量级,其在次表层表现更突出,而这印证了实际大洋中次表层海温的重要性,并表明ENSO现象与海洋赤道Kelvin波慢波模态关系密切。
5)将该波的第二模态与实际热带太平洋和印度洋的实况及诊断作对比后知,该模态能对实际赤道大洋情况在某种程度上加以解释。
本文求得的是二层海洋中Kelvin波最简单的解析解模态,而实际大洋情况更加复杂。所以,本文中Kelvin波第二模态与实况有某些差异也是正常的。然而,本文Kelvin波第二模态的确在某种程度上能够对实况做出解释;这表明实际大洋中确实存在赤道海洋Kelvin波的慢波模态,其与本文Kelvin波第二模态相类似,故而本文工作是有意义的。
参考文献(References):
[1] LIU F,LUO Y,LU J,et al.Response of the tropical Pacific Ocean to El Niño versus global warming[J].Climate Dynamics,2016:1-22.
[2] FENG J,WANG Q,HU S,et al.Intraseasonal variability of the tropical Pacific subsurface temperature in the two flavours of El Niño [J].International Journal of Climatology,2016,36(2):867-884.
[3] DU Y,LIU K,ZHUANG W,et al.The Kelvin wave processes in the equatorial Indian Ocean during the 2006—2008 IOD events[J].Atmospheric&Oceanic Science Letters,2012,5(4):324-328.
[4] ZHENG F,ZHU J.Observed splitting eastbound propagation of subsurface warm water over the equatorial Pacific in early 2014[J].Science Bulletin,2015,60(4):477-482.
[5] YU F,WANG Q.The interannual variabilities of the Pacific north equatorial countercurrent and influencing factors[J].Periodical of O-cean University of China(Natural Science),2016,46(2):6-13.于飞,王启.太平洋北赤道逆流年际变化的特征及其影响因子分析[J].中国海洋大学学报(自然科学版),2016,46(2):6-13.
[6] MOSQUERA K V,DEWITTE B,ILLIG S.The central Pacific El Niño interseasonal Kelvin wave[J].Journal of Geophysical Research Oceans,2014,119(10):6605-6621.
[7] CAO G J.Oceanic interseasonal variability in the Indonesian throughflow and its adjacent regions[D].Qingdao:The First Institute of Oceanography,SOA,2015.曹国娇.印度尼西亚贯穿流及其周边海域海洋季节内变化研究[D].青岛:国家海洋局第一海洋研究所,2015.
[8] ZHANG D L,HE J X.Dynamic statistic diagnosis of upper currentin tropical Indian Ocean[J].Climatic and Environmental Research, 2005,10(3):387-400.张东凌,何卷雄.热带印度洋上层洋流的动力统计诊断[J].气候与环境研究,2005,10(3):387-400.
[9] LU X,ZHANG D L.A statistical diagnosis of upper-ocean currents in tropical Pacific Ocean in May[J].Journal of Tropical Oceanography,2009,28(2):22-30.卢姁,张东凌.热带太平洋5月份上层洋流的动力统计诊断[J].热带海洋学报,2009,28(2):22-30.
[10] HUANG P,LIN I I,CHOU C,et al.Change in ocean subsurface environment to suppress tropical cyclone intensification under global warming[J].Nature Communications,2015,6,doi:10.1038/ncomms8188.
[11] LI S,JIA M,GAO J,et al.Decadal characterization of Indo-Pacific Ocean subsurface temperature modes in SODA reanalysis[J].Journal of Climate,2015,28(15):6113-6132.
[12] LI X,LI C Y.Occurrence of two types of El Niño events and the subsurface ocean temperature anomalies in the equatorial Pacific[J]. Chinese Science Bulletin,2014,59(21):2098-2107.黎鑫,李崇银.两类El Niño的发生与赤道太平洋次表层海温异常[J].科学通报, 2014,59(21):2098-2107.
[13] CHEN Y L,ZHAO Y P,ZHANG M N,et al.The characteristics of interannual and interdecadal variability of equatorial Pacific Ocean temperature anomalies and ENSO cycle[J].Haiyang Xuebao,2005,27(2):39-45.陈永利,赵永平,张勐宁,等.赤道太平洋次表层海温异常年际和年代际变率特征及其与ENSO循环[J].海洋学报,2005,27(2):39-45.
[14] LI F.Characteristics of interannual variability of east Asian summer monsoon and its links with the subsurface tropical Pacific SST[D]. Nanjing:Nanjing Information Engineering University,2015.李锋.东亚夏季风年际变化特征及其与热带太平洋次表层海温的联系[D].南京:南京信息工程大学,2015.
[15] MATSUNO T.Quasi-geostrophic motion in the equatorial area[J].Journal of the Meterorological Society of Japan,1966,44(1):25-43.
[16] ZENG Q C.Numerical weather prediction mathematical physical basis:first volume[M].Beijing:Science Press,1979:230-237.曾庆存.数值天气预报的数学物理基础:第一卷[M].北京:科学出版社,1979:230-237.
[17] ZHAO Y P,CHEN Y L,ZHANG M N,et al.Evolution characteristics of the subsurface temperature anomaly in the equatorial Pacific to two pattern ENSO events[J].Advances in Water Science,2006,17(1):7-13.赵永平,陈永利,张勐宁,等.两类ENSO事件赤道太平洋次表层海温异常的演变特征[J].水科学进展,2006,17(1):7-13.
[18] WANG L,ZHANG W J,QI I,et al.Contrasting air-sea features associated with two types of La Niña during the seasonal evolution[J]. Haiyang Xuebao,2014,36(1):72-85.王磊,张文君,祁莉,等.两类La Niña季节演变过程的海气耦合特征对比[J].海洋学报,2014, 36(1):72-85.
[19] ZHANG M,ZHANG L F.Spectral analysis of spherical barotropic atmosphere[J].Chinese Journal of Hydrodynamics:Series A,2006, 21(1):130-138.张铭,张立凤.球面正压大气的波谱分析[J].水动力学研究与进展:A辑,2006,21(1):130-138.
[20] LIU T,CHEN C C,MILOR L.Accurate standard cell characterization and statistical timing analysis using muttivariate adaptive regression splines[C]∥IEEE.International Symposium on Quality Eleotronic Design(ISQED),2015:272-279.
[21] HOUGHTON R W,TOURRE Y.Characteristic of low-frequency sea surface temperature fluctuations in the tropical Atlantic[J].Journal of Climate,1992,5(7):765-771.
[22] XUAN L L,QIU Y,XU J D.Seasonal variation of surface-layer circulation in the eastern tropical Indian Ocean[J].Journal of Tropical Oceanography,2014,33(1):26-35.宣莉莉,邱云,许金电.热带东印度洋表层环流季节变化特征研究[J].热带海洋学报,2014,33 (1):26-35.
Analytical Solutions of the Two-layer Oceanic Equatorial Kelvin Wave
LU Xu1,2,LU Kai-cheng1,2,ZHANG Ming2
(1.Unit 61741,PLA,Beijing 100094,China;2.Laboratory of Atmospheric Circulation and Short-range Climate Forecast, College of Meteorology and Oceanography,PLA University of Science and Technology,Nanjing 211101,China)
Analytical solutions of oceanic equatorial Kelvin wave were achieved based on two-layer linear perturbation equations with equatorial beta-plane approximation.The results show that this equatorial Kelvin wave has two modes.The current fields of upper-layer and lower-layer of the two modes are both eastward zonal flow,which peaks at the equator and decays with the increase of latitude.The two modes are non-dispersive.All of these features are same as those of classic Kelvin wave.The phase velocity of the first mode(the former)is two orders of magnitude larger than that of the second mode(the latter).The phase velocity of the latter was close to the ocean current speed.The former is a fast-wave mode,of which the period was about half a day,while the latter is a slow-wave mode,of which the period was about one season,and has important implications for climate.The attenuation of flow fields of first mode is much faster than that of the second mode,and the latter is more of equatorial captured wave.The meridional attenuation of the potential field in each layer of the two modes is similar to the flow field.The latter agrees well with the observed wave dynamics of the tropical Indian Ocean and Pacific Ocean,and can explain some phenomena in equatorial oceans and ENSO.
two-layer oceanic model;equatorial Kelvin wave;modal analysis;analytical solution;subsurface layer
August 8,2016
P732
A
1671-6647(2017)03-0337-13
10.3969/j.issn.1671-6647.2017.03.004
2016-08-08
国家重点基础研究发展计划项目——西北太平洋海洋多尺度变化过程、机理及可预报性(2013CB956203)
卢 姁(1982-),女,江苏南通人,工程师,博士,主要从事气候方面研究.E-mail:xlu2006918@163.com
