基于高斯消元法下的最佳平方逼近算法效率分析——以一道ACM试题为例

罗 兴 钱佳威

(江西财经大学软件与通信工程学院 江西 南昌 330032)



基于高斯消元法下的最佳平方逼近算法效率分析
——以一道ACM试题为例

罗 兴 钱佳威

(江西财经大学软件与通信工程学院 江西 南昌 330032)

针对ACM数值计算分析类的防AK试题，一般可以利用克拉默法则最佳平方逼近、高斯消元最佳平方逼近、Hilbert矩阵Cholesky分解平方逼近和切比雪夫多项式正交等方法求解。以第39届ACM-ICPC西安邀请赛的一道防AK题为例，对这几种典型算法进行实验分析，并在反复实验中对算法参数进行修正，然后进行质量与效率的分析。测试结果表明，高精度高斯消元最佳平方逼近解法求解ACM数值计算分析类的防AK试题，优于克拉默法则最佳平方逼近、普通高斯消元最佳平方逼近和Hilbert矩阵Cholesky分解平方逼近，是解决数值计算分析类问题的一种有效方法。

数值计算分析 ACM-ICPC 最佳平方逼近 算法 Hilbert矩阵

0 引 言

1 预备计算数学知识

1.1 函数的p-范数下的距离(L^p空间)

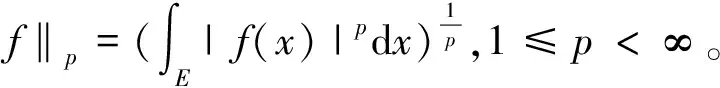
1.2 最佳一致逼近

1.3 最佳平方逼近函数

1.4 正交多项式

1.5 克拉默法则

含有n个未知数x1,x2,…,xn的n个线性方程的方程组:

与二、三元线性方程组类似，它的解可以用n阶行列式不等于零，即：

那么，上述方程组有唯一解：

其中Dj(j=1,2,…,n)是把系数行列式D中第j列的元素用方程组右端的常数项代替后所得到的n阶行列式，即[5]:

1.6 高斯消元法解方程

若用初等行变换将增广矩阵(AB)化为(CD)，则AX=B与CX=D是同解方程组。所以我们可以用初等行变换把增广矩阵转换为行阶梯阵，然后回代求出方程的解[6]。

1.7 Hilbert矩阵的行列式值递推关系

Hilbert矩阵的特性：Hilbert矩阵是非奇异的对称正定矩阵,对Hilbert矩阵的兴趣主要在于它是严重病态的,其条件数随n增加而快速增大[7]，其中可以推出希尔伯特矩阵是存在一般的递推式，其行列式递推关系式子如下：

det(H1)=1

1.8 切比雪夫正交多项式法

1.9 最佳平方元逼近方法

已知内积空间C[a,b]，si∈C[a,b],i=0,1,2,…,n是一个函数S的一组基函数,对给定f(x)于内积空间内。可以使用由S空间内的一组基作为最佳平方逼近元来逼近f(x)。又因为，最佳平方逼近元与其逼近函数之间的差值函数必须与空间内所有基底均正交，也就引出法方程。

第一步利用前面的权函数为1时建立法方程：

第二步解方程，若S空间下的基底为一组正交基则直接可以得出：

在对于非正交基的情况下，需要用多种方法来解方程。

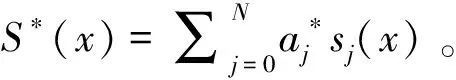
1.10 基于Cholesky法解方程

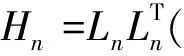
2 原问题的模型化解分析

2.1 利用普通最佳平方逼近法(包括克拉默和高斯消元法)

参考上述1.8节有如下步骤：

(2) 列出法方程为：

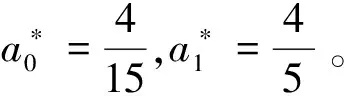
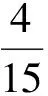
2.2 正交多项式法

在进行法方程解决时可以采取一些变换使得问题更加容易解决，例如正交化的方法，参考上面切比雪夫多项式概要解法，有如下步骤：

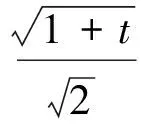
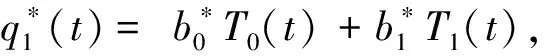
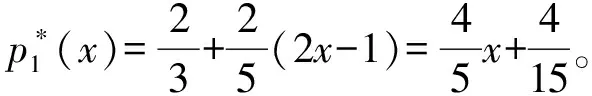
3 原问题的多种解法及其分析

3.1 最佳平方逼近原理的法方程推导

原问题与上述模型化解分析后的问题相比还有一个更特殊的情况，其法方程系数矩阵为希尔伯特矩阵(该矩阵是一个病态矩阵)。由于精度丢失严重，也就是说在用高斯消元法时必须要超过50位(大概是65～75位)的高精度地保留每一个系数。

证明如下：

3.2 基于切比雪夫正交多项式解法

3.3 基于克拉默法则的最佳平方逼近解法

在处理线性方程组候，如1.5节，利用克拉默法则处理，对系数矩阵D高精度保存，约为65～75位精度。求出其行列式的值(可用初等变换或者递归降次法)，接着分别求出：

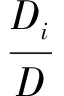
3.4 基于高斯消元法的最佳平方逼近解法

在求解线性方程组时，如1.6节，利用高斯消元法处理，对增广矩阵高精度保存，约为65～75位精度。对该矩阵进行初等行变换，使得该矩阵每一行只有至多三个非零系数。并且呈阶梯状，然后用值进行回代解出xi,i=0,1,2,…,n。这种方法的时间复杂度为O(n3logn)，主要时间消耗取决于高斯消元法的解步骤。

3.5 基于希尔伯特矩阵下的Cholesky分解最佳平方逼近解法

从1.7节与1.10节可知，希尔伯特矩阵在Cholesky分解后的行列式求解直接对角元素求解，所以在求行列式D上面，速度远快于克拉默法则下的逼近算法，并且求逆矩阵有很快的方法，最后就是两次矩阵乘以向量计算。在速度上面接近于正交多项式法。

4 实验数据分析

数据分析一：高斯消元法的最佳平方逼近解法实验得出如下数据(精确定50位从a0到aN的值):1，5，11，49。

N=1

a0=0.8731273138361809414411498854106499910289

883747998382999

a1=1.6903090292457285878382751718840250134565

174378002425502

Time = 0 ms

N=5

a0=0.9999975939486582685846763425946823321929

666903704104120

a1=1.0000998014733356176039702748826807813478

983478455885884

a2=0.4990191752274595967912934050764328896781

377014278964404

a3=0.1704895390402274037395388939937569965983

870278785847299

a4=0.0348011156854306817682964311699413924928

142869551933373

a5=0.0138720048045378305279050793524077040967

542874206272326

Time = 16 ms

N=11

a0=0.9999999999999987463423319146710162243966

416742831149886

a1=1.0000000000001949307430616128638689626054

795315828574704

a2=0.4999999999925241103946606592514405054594

937593838801533

a3=0.1666666667906898665617204147849644463615

430318949024408

a4=0.0416666655567319300955711299291532518750

378322723241546

略去部分数据

Time = 31 ms

N=49

a0=0.9999966116019126567946264201524917677909

448251223809396

a1=1.0082998895844076840339140654323540177602

496445702108691

略去部分数据

Time = 790 ms

数据分析二：

表1 不同算法的耗时分析比较(试题允许时间：5 000 ms)

数据分析三：

(1) 基于切比雪夫正交多项式解法在试题允许的时间内只能计算出14项以内的系数值；

(2) 基于克拉默法则的最佳平方逼近解法在试题允许的时间内只能计算出6项以内的系数值；

(3) 基于希尔伯特矩阵下Cholesky分解解法在试题允许的时间内只能计算出13项以内的系数值；

(4) 基于高斯消元法的最佳平方逼近解法在试题允许的时间内可轻松计算出试题所要求的系数值。

5 结 语

对于此高精度问题，由于Java引入BigDecimal数据类型，保留高精度计算不再成为一件很难的事情了。在这种情况下，基于高斯消元法的最佳平方逼近解法的效率和精度上要快于和大于希尔伯特矩阵Cholesky分解法，同时也要远快于和大于基于克拉默法则的最佳平方逼近解法。在精度丢失这一块要小于希尔伯特矩阵Cholesky分解法，由高精度数据类型的引入，从权衡计算效率和精度而言，高斯消元法的最佳平方逼近还是优于希尔伯特矩阵Cholesky分解法。所以，最优化的解法是基于高精度的高斯消元法的最佳平方逼近解法。而这些不同算法的差距主要体现在求解法方程时所使用的解线性方程组的方式。

[1] 周民强.实变函数论[M].北京:北京大学出版社,2008.

[2] 李国林.切比雪夫最佳一致逼近法及误差函数特性研究[J].西华师范大学学报(自然科学版),2007,28(3):253-256.

[3] 黄铎,陈兰平,王风.数值分析[M].北京:科学出版社,2000.

[4] 刘田,谈进.正交多项式逼近下非线性趋势序列单位根检验[J].统计研究,2011,28(4):99-105.

[5] 同济大学数学系.线性代数[M].北京:高等教育出版社,2011.

[6] 李汉霖.高斯消元法及其在信息学中的应用[J].科技论坛,2015(16):85-86.

[7] 李燕.关于系数矩阵为Hilbert矩阵的线性方程组的思考[J].新疆大学学报(自然科学版),2005,22(2):165-167.

[8] 赵金伟.基于正交多项式核函数方法[J].计算机技术与发展,2012,22(5):177-179.

EFFICIENCYANALYSISOFOPTIMALSQUAREAPPROXIMATIONALGORITHMBASEDONGAUSSIANELIMINATIONMETHOD:ANEXAMPLEOFQUESTIONABOUTACM

Luo Xing Qian Jiawei
(SchoolofSoftwareandCommunicationEngineering,JiangxiUniversityofFinanceandEconomics,Nanchang330032,Jiangxi,China)

Aiming at the anti-AK problem of ACM numerical analysis, we generally use the best square approaching based on Cramer Rule, the best squared approaching of the Gaussian elimination, the square approaching under Cholesky decomposition of the Hilbert matrix and the Chebyshev polynomial Orthogonal method solution. In this article, we take an anti-AK problem in the 39th ACM-ICPC Xi'an Invitational Tournament as an example to analyze the typical algorithms and modify the algorithm parameters in repeated experiments. The test results showed that the best squared approximation of the Gaussian elimination method was an effective method to solve anti-AK problem of ACM numerical analysis, which is better than the best square approximation of the ordinary Gaussian elimination and the square approximation of the Cholesky factorization of the Hilbert matrix.

Numerical calculation analysis ACM-ICPC Best square approaching Algorithm Hilbert matrix

2016-11-30。罗兴，本科生，主研领域：软件工程。钱佳威，本科生。

TP301.6

A

10.3969/j.issn.1000-386x.2017.08.052