基于WFRFT的混合载波系统资源分配算法

牛红威，叶 亮，李卓明，石纪福

(1.哈尔滨工业大学 电子与信息工程学院，黑龙江 哈尔滨 150001 ；2. 通信网信息传输与分发技术重点实验室，河北 石家庄 050081)



基于WFRFT的混合载波系统资源分配算法

牛红威1,2，叶 亮1，李卓明1，石纪福1,2

(1.哈尔滨工业大学 电子与信息工程学院，黑龙江 哈尔滨 150001 ；2. 通信网信息传输与分发技术重点实验室，河北 石家庄 050081)

在时频双弥散信道下，传统频域资源分配算法对基于WFRFT的混合载波系统难以起到良好改善作用，针对此问题，提出一种在分数域上进行资源分配的改进算法。分数域是由传统时/频域扩展而来，对于信道的实际环境考虑全面。算法基于分数域理论基础，在分数阶次上传输发射信号，从而提升通信系统的整体性能。仿真结果表明，对于混合载波系统而言，改进算法较频域资源分配算法有更好的比特误码率性能。

WFRFT; 双弥散信道; 混合载波; 分数域; 资源分配

0 引言

现如今信道环境变得越来越复杂，在快速时变的信道条件下，通信双方频繁的高速移动将引起较大的多普勒频移，出现频率弥散，进而导致通信系统的接收信号发生频谱扩展，严重破坏了多载波系统中子载波间的正交性，产生载波间干扰[1](Inter Carrier Interference， ICI )，降低通信系统的性能。另一方面，多径效应会带来时间弥散，产生符号间干扰[2](Inter Symbol Interference， ISI )，通常很难同时抑制这2种干扰。例如，正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)系统能够减小ISI，但对ICI却十分敏感。因此，传统的OFDM技术和单载波频域均衡(Single Carrier Frequency Domain Equalization，SC-FDE)技术都不适用于频域、时域双弥散信道。

此外，4G移动通信技术已经普及，5G技术也进入了研发阶段，通信数据量呈爆炸式增长，无线资源日益紧张，因此合理的资源分配算法对于当前的无线通信系统来说至关重要。但是传统的资源分配模型都是在频域上进行的[3-4]，这不仅没有考虑到双弥散信道的时变性，而且难以对基于WFRFT的混合载波系统起到良好的性能改善作用。

针对上述问题，在基于Jakes模型构建时频双弥散信道的基础上，引入具有良好抗ICI/ISI能力的混合载波系统，并提出对该系统进行分数域上的资源分配，相比于传统的频域资源分配算法，该算法综合考虑了时变的信道环境与分数阶次的发送信号，性能上也有了一定程度的提升。

1 系统模型

1.1 混合载波系统

经典加权类分数傅里叶变换WFRFT是将时域信号g(x)及其反转g(-x)，频域信号G(x)及其反转G(-x)4个信号通过线性加权的形式表示[5]为:

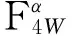
w2(α)g(-x)+w3(α)G(-x)，

(1)

式中，加权系数wl(a)表示为:

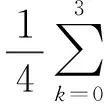
(2)

图1给出了用4-WFRFT实现时频联合分析的框图。输入信号经过串并转换后分为4个支路信号输出，分别为w0、w1、w2、w3。其中，w0和w2相当于时域SC系统中的信号，直接传输；而w1和w3相当于频域OFDM系统中的信号，经历了DFT变换。因此，输出信号中包含单载波信号和多载波信号，体现出混合载波调制系统的特性[6]。

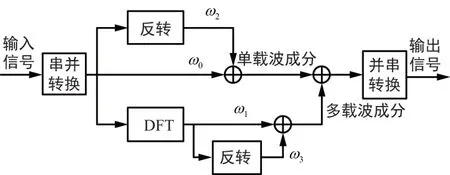
图1 4-WFRFT结构框图

1.2 时频双弥散信道

时频双选衰落信道是一种广义平稳非相关散射信道[7-8]，构建这种信道必须考虑到频率弥散。先用Jakes模型产生单径Rayleigh信道，然后再扩展单径Jakes模型，得到一个由L个彼此独立的指数特性衰落信道叠加而成的信道模型。

通过正弦波叠加对Jakes模型建模，并假设信道中可分辨径的强度相近，那么时间连续信道复增益：

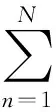
(3)

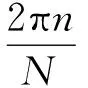
取N/2为奇数，式(3)改写为：

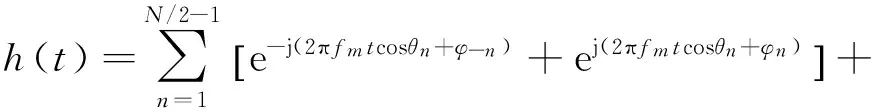
(4)

Jakes信道模型使用的是互不重复的频率，则式(4)中h(t)的表达式变为：

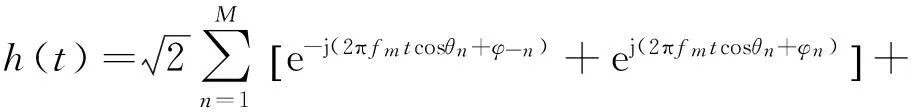
(5)

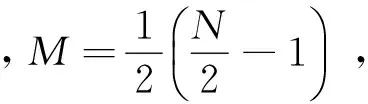
h(t)=hI(t)+jhQ(t)=

(6)

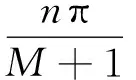
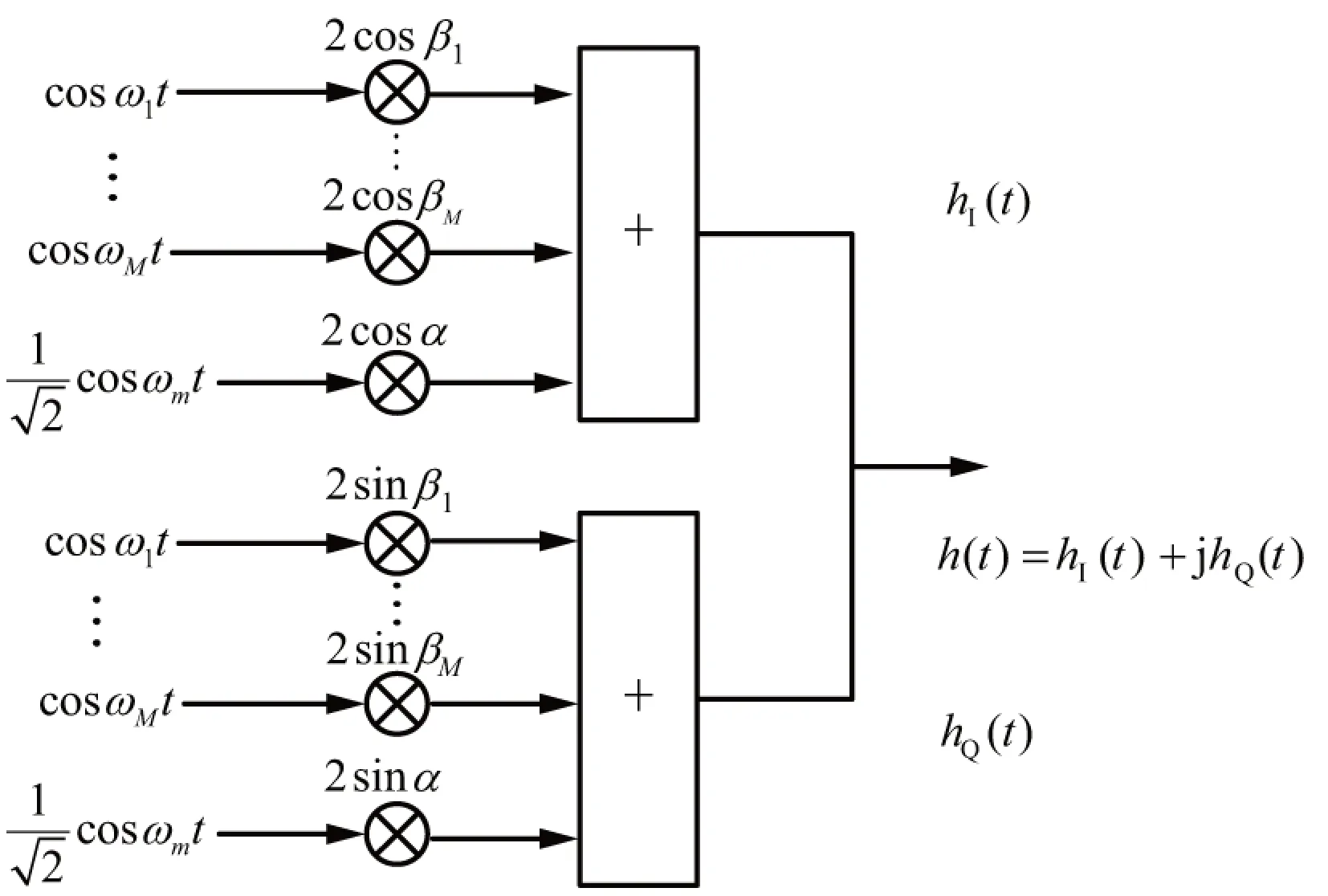
图2 Jakes仿真器结构图

2 资源分配算法

2.1 加权分数傅里叶变换域

时域接收信号yt变换为对应的a阶WFRFT域接收信号可表示为：

yα=Fαyt=Fα-1Y=

FαHtx+Fαv=

Fα-1HdfX+Fα-1w=

Hαxα+Fαv，

(7)

式中，x、X和xa表示发射信号的时域、频域和分数域形式，v和w表示时域和频域的噪声信号，Ht和Hdf表示衰落信道的时域和频域信道矩阵[9]，根据式(7)，a阶WFRFT域信道矩阵可写作：

Hα=FαHtF-α=Fα-1HdfF1-α。

(8)

为求得式(8)中的Ha，首先对发射端的时域信号x进行WFRFT变换，得到α阶WFRFT域信号xa：

xα=Fαx=
w0(α)x+w1(α)F+w2(α)F2x+w3(α)F3x。

(9)

进而从式(9)中可以推出WFRFT矩阵Fa的表达式为：

麦肯锡全球研究所给出“大数据”的定义是：一种规模大到在获取、存储、管理、分析方面大大超出了传统数据库软件工具能力范围的数据集合，具有量大、类型多、价值高、处理速度快四大特征。通俗的讲，大数据指的就是对大量的、不同类型的数据信息进行的集合，这种数据信息可以是数字，也可以是文字资料，比如，某个客户的具体信息，包括姓名、性别、联系方式、看好等。大数据的收集能为企业带来精确的市场预测，使企业的发展战略更加精准。那么，为了顺应时代发展趋势，让成本数据更好地为企业管理决策服务，就需要发挥大数据的优势。

Fα=w0(α)I+w1(α)F+w2(α)F2+w3(α)F3。

(10)

为了可以更清晰具体地分析所构建的时频双选信道的矩阵结构随阶次α的取值变化的情况，引入了WFRFT域信道矩阵，进而更方便后文进行分数域上的资源分配。

2.2 分数域资源分配算法

频选衰落信道是慢变的，资源分配算法只需考虑频域。但时频双选衰落信道的时变是快变的，且其信道频率分量随时间的变化而变化。在这种情况下会出现频率弥散，使频域信道矩阵Hdf不再呈现理想的对角阵结构，传统频域资源分配算法不再适用。

由式(7)中给出的ya表达式，可知第k个子载波上的WFRFT域接收信号ya(k)可表示为：

yα(k) =Hα(k,k)xα(k)+

(11)

式中，第一项是系统的期望值，第二项是WFRFT的域间干扰，则第k个子载波的SINR为：

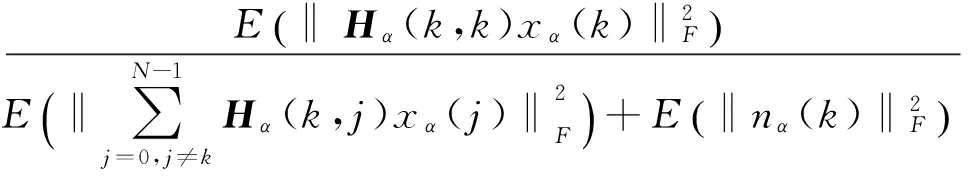
(12)

如前面所述，在时频双弥散信道下，频域信道矩阵不再呈理想的对角阵结构。为削弱上式第二项域间干扰，寻找在主对角线处显示良好聚集特性的分数域信道矩阵来传输信号。基于此，对分数域发送信号xa进行资源分配，其依据是选择Ha主对角线上的各个瞬时信道增益，这样可以很大程度上确保信息比特准确传输，提升系统误比特性能。

图3给出了双弥散信道的时域、频域和分数域(α=0.2)信道矩阵的分布，可见在该信道条件下，Ht和Ha的分布更接近于对角阵结构，而Hdf的频率弥散现象比较严重。说明要想显著提升混合载波(Hybrid Carrier，HC)系统的传输性能，可以选择在低阶次上对分数域发送信号进行资源分配。

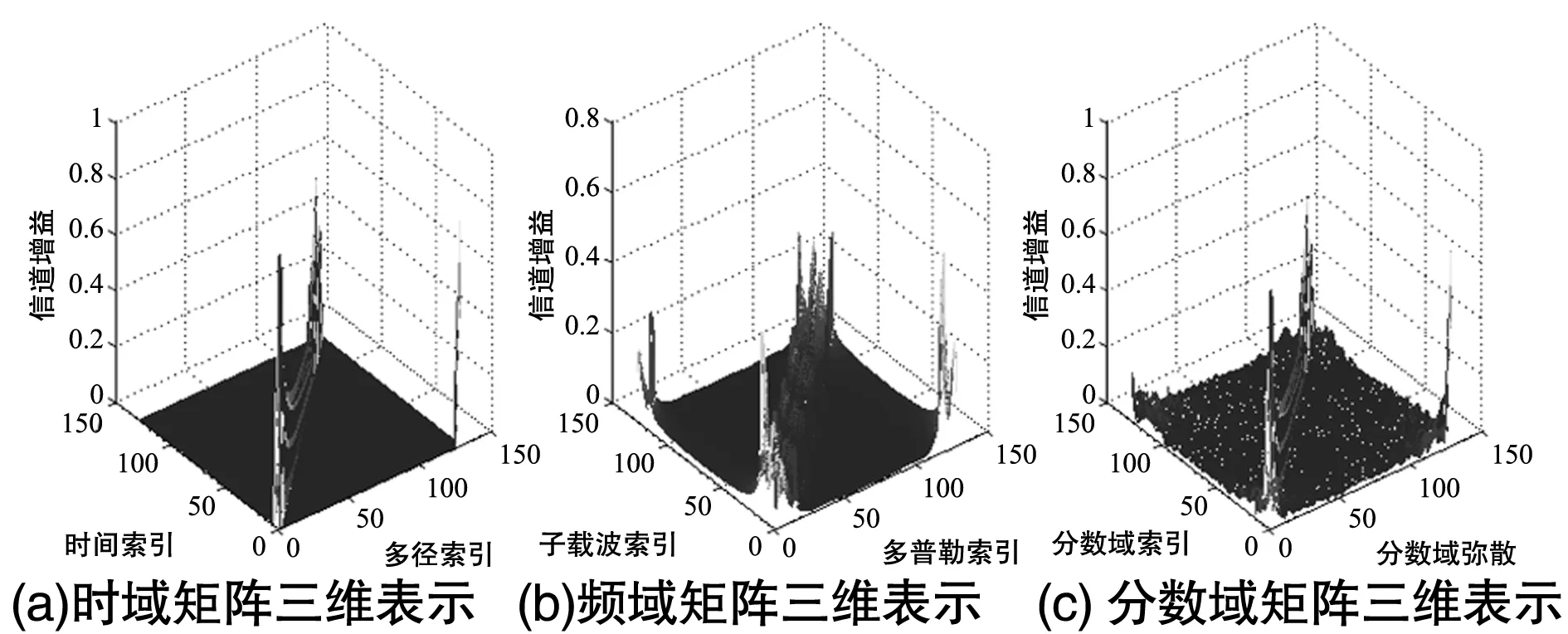
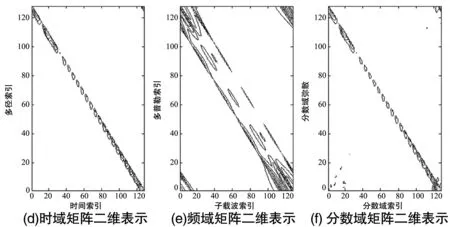
图3 信道矩阵的分布

3 仿真分析

在给定时频双弥散信道，其中同时包含了5条路径，且最大多普勒频移满足fm×T=0.02，子载波数为128个，对SC、OFDM、HC(a=0.5)系统的误比特性能进行仿真比较，结果如图4所示。

从图4中可以看出，在给定的信道条件下，混合载波系统(HC)在高信噪比时性能明显优于传统的单载波(SC)和多载波系统(OFDM)，综合了二者在抗ICI/ISI方面的优势，能有效地抵抗时频双衰落的影响。

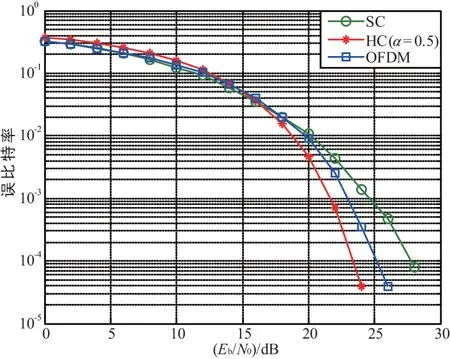
图4 3种载波体制的误比特性能

在给定包含5条路径的时频双弥散信道，fm×T=0.02，采样周期为2×10-6s，子载波数为128个，采用频域迫零(Zero-Force，ZF)均衡。通过仿真验证SC系统、OFDM系统和HC(α=0.2)系统中分数域资源分配算法的有效性，结果如图5所示。

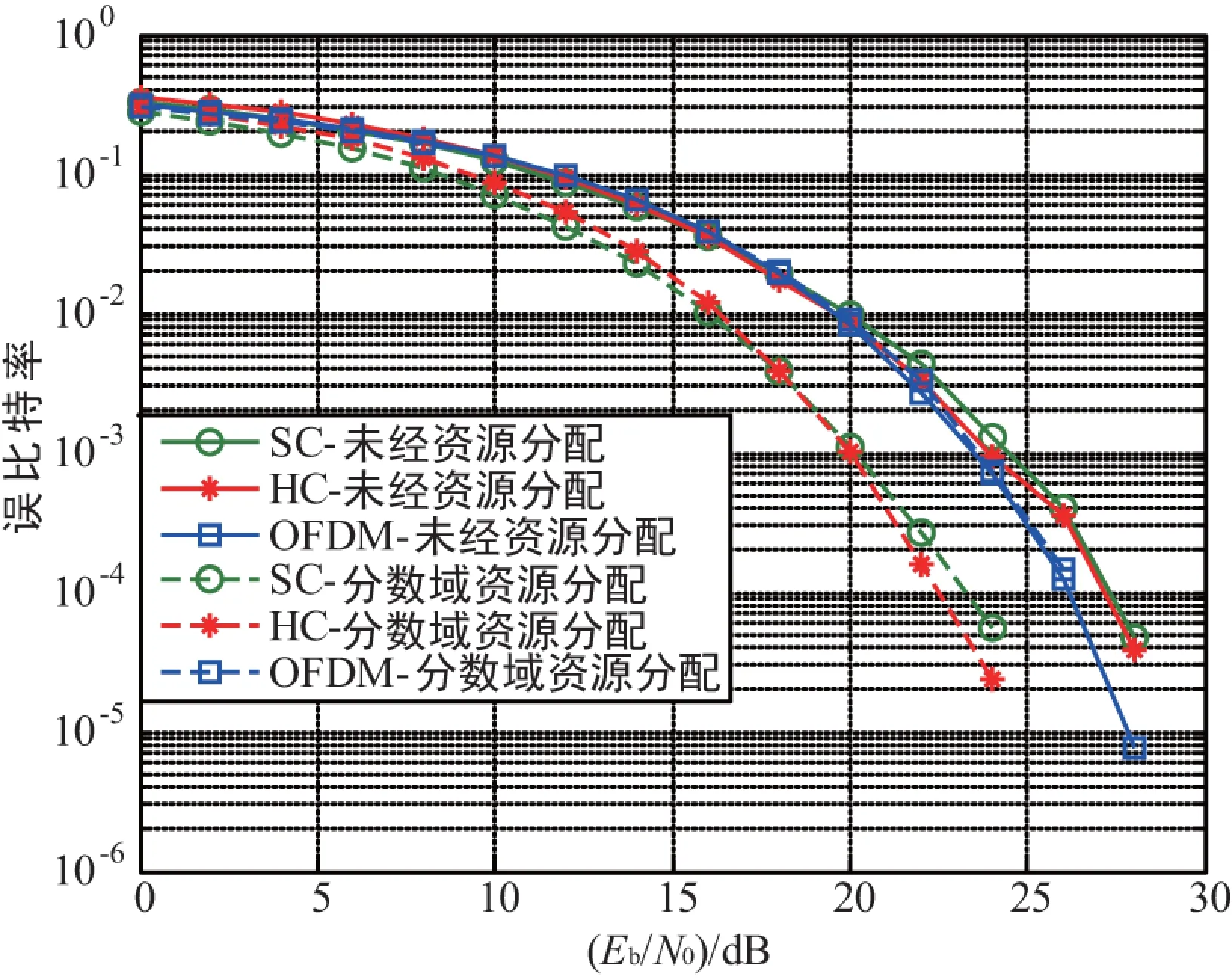
图5 3种载波体制有无分数域资源分配的误比特性能

从图5中可以看出，采用了分数域资源分配算法的SC系统、OFDM系统和HC(α=0.2)系统相比未采用分数域资源分配算法的BER性能有所提升，尤其是SC系统和HC系统，例如BER=10-4时，其信噪比改善了约5 dB。信道矩阵的近似对角结构是SC和HC系统性能改善的主要原因，对角阵结构能够很大程度地降低非主对角线上弥散产生的域间干扰。

此外值得注意的是，未采用分数域资源分配算法的HC系统的BER性能劣于OFDM系统，但采用了资源分配算法之后，其性能却明显优于OFDM系统。而OFDM系统的BER性能则在采用分数域资源分配算法前后几乎没有变化，类似的，SC系统的BER性能也几乎没有变化。由此可知，当系统在距离资源分配所在阶次较远的时候，是否进行资源分配对系统性能没有较大影响，而对于所在阶次或在该阶次附近的分数域信号，其BER性能能够得到显著的提升。

归结其原因，传统的频域资源分配算法只能解决系统的频域深衰落问题，虽然能够提升多载波系统如OFDM的传输性能，但随着α的减小，系统中的单载波分量增加，资源分配算法对分数域信号的效果变差。同样地，时域资源分配算法只能解决系统的时域深衰落问题，虽然能够提升单载波系统SC的传输性能，但随着α的增大，系统中的多载波分量增加，资源分配算法对分数域信号的效果变差。通过调整分数域资源分配算法的阶次，可以使系统根据需要抑制不同的衰落问题。

接下来，基于相同的仿真条件，对比采用频域资源分配算法的HC系统与采用分数域(α=0.2)资源分配算法的HC系统的性能。图6给出仿真对比结果。

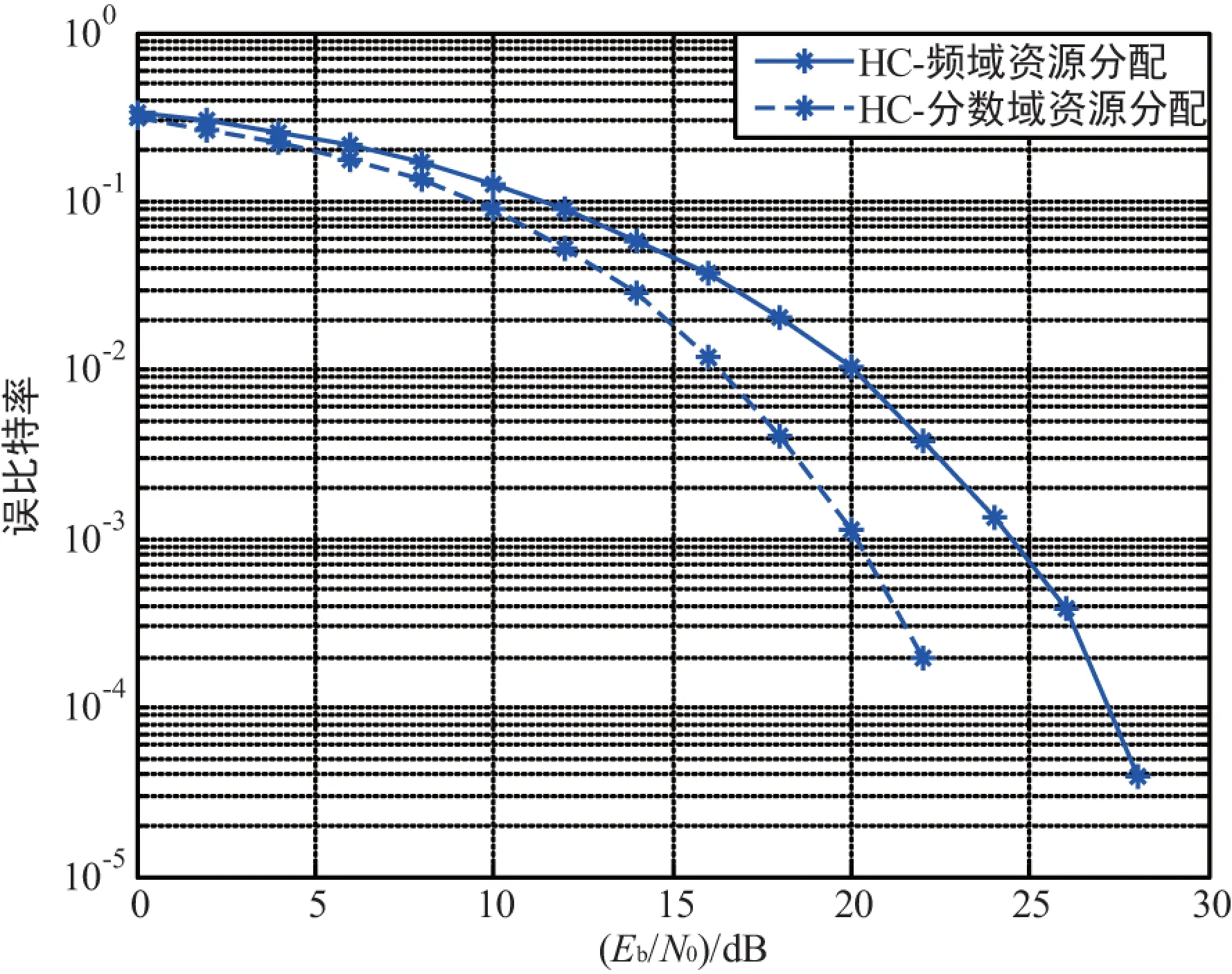
图6 分数域资源分配与频域资源分配

从图6中可以看出，采用了0.2阶分数域资源分配算法的HC系统与采用频域资源分配算法的HC系统相比，误比特性能有较显著的改善。BER=10-4时，系统的SNR得到了5 dB的改善。参照图5的仿真结果，采用频域资源分配(相当于α=1的分数域)算法对低阶次(α=0.2)HC系统几乎没有改善效果。这是因为Hdf发生了频率弥散，而阶次相差较远。

综上所述，在时频双弥散信道下，当HC系统采用相应(或相近)阶次的分数域资源分配算法时，系统性能的提升才会更加显著，从而以更大的效率去利用无线频带资源。

4 结束语

由于信道环境的高速性复杂性，传统的多载波和单载波体制在时频双弥散信道下不能再体现出良好的性能。然而通过时频联合工具WFRFT可以将二者融合在一起，让信号能量能够更加均匀地分布在时频平面上，因此在抗时频双衰落时表现出独特的优势，同时也解决了现有通信系统中单载波(SC)和多载波(OFDM)体制不兼容的问题，弥补各自的缺陷，取长补短，因此基于WFRFT的混合载波系统达到了提高系统性能以及提高频带利用率的目的，进一步实现了将发送信号最佳适应于时变的信道环境。

由于无线资源的日益紧缺性，在时频双弥散信道下对提出的混合系统进行相应阶次的分数域资源分配，因其能够考虑信道的实际环境，并能在相应分数阶次上充分传输信号，故能更加显著地改善系统性能，进而更有效率地利用无线频带资源。

[1] Nessel R,Rupp M.Doubly-selective MMSE Channel Estimation and ICI Mitigation for OFDM Systems [C]∥International Conference on Communications(ICC). IEEE,2015：4692-4697.

[2] Barriac G D,Howard S J,Gore D A. Removal of ICI/ISI Errors in Frequency Domain Channel Estimation for Wireless Repeaters: US,US 20110116392 A1[P],2011.

[3] Krishnan K V,Bagubali A,Khara S. Dynamic Resource Allocation in OFDM-Based Cognitive Radio System Based on Estimated Channel Information [C]∥ Proceedings of the International Conference on Soft Computing Systems. Springer India,2016：949-955.

[4] Guo X,Zhang S,Guo L,et al. An Improved Dynamic Resource Allocation in Multi-users OFDM System [M]. India :Springer,2016：741-748.

[5] Shih C C. Fractionalization of Fourier Transform[J]. Optics Communications,1995,118:495-498.

[6] Mei Lin,Sha Xuejun,Zhang Naitong.The Approach to Carrier Scheme Convergence Based on 4-Weighted Fractional Fourier Transform [J]. IEEE Communications Letters,2010,14(6)：503-505.

[7] Said K,Beex A A L.Per-symbol ICI Mitigation for Low-dimensional Doubly Dispersive Channels Using Pilot Restoration[C]∥International Symposium on Signal Processing and Information Technology(ISSPIT).IEEE,2015：460-465.

[8] Zhao Y,Chen X,Xue L,et al.Design of Robust Pulses to Insufficient Synchronization for OFDM/OQAM Systems in Doubly Dispersive Channels[J].Mathematical Problems in Engineering,2015:1-10.

[9] 王焜. 基于加权分数傅立叶变换的双选信道下干扰抑制方法研究[D]. 哈尔滨：哈尔滨工业大学,2014.

[10]刘晨,沙学军,张文彬,等. 积分判决的高效协同信号调制解调方法[J]. 哈尔滨工业大学学报,2015,47(3):29-35.

[11]Fang Xiaojie,Sha Xuejun,Li Yong. Secret Communication Using Parallel Combinatory Spreading WFRFT[J].IEEE Communications Letters,2015,19(1):62-65.

[12]Fang Xiaojie,Sha Xuejun,Mei Lin. Guaranteeing Wireless Communication Security via a WFRFT-based Cooperative System[J]. China Communications,2015,12(9):76-82.

[13]Li Yong, Sha Xuejun,Zheng Fuchun,et al. Low Complexity Equalization of HCM Systems with DPFFT Demodulation over Doubly-selective Channels[J]. IEEE Signal Processing Letters,2014,21(7):862-865.

Resource Allocation Algorithm for Hybrid Carrier System Based on WFRFT

NIU Hong-wei1,2,YE Liang1,LI Zhuo-ming1,SHI Ji-fu1,2

(1. School of Electronics and Information Engineering,Harbin Institute of Technology,Harbin Heilongjiang 150001,China; 2. Science and Technology on Information Transmission and Dissemination in Communication Networks Laboratory,Shijiazhuang Hebei 050081,China)

In time-frequency doubly dispersive channels,traditional frequency domain resource allocation algorithms cannot make good improvement for hybrid carrier systems based on WFRFT. To overcome this problem,an improved algorithm of resource allocation in fractional domain is proposed. Fractional domain is an extension of traditional time/frequency domain,and can comprehensively consider the actual channel environment. The improved algorithm is developed in the fractional domain,and can fully send the transmission signals on the matching fractional order,thus maximizes overall performance of the system. Simulation results show that the proposed algorithm has a better bit error rate performance than the frequency domain resource allocation algorithm for hybrid carrier systems.

WFRFT; doubly dispersive channel; hybrid carrier; fractional domain; resource allocation

2017-05-07

国家自然科学基金项目(61602127)；国家 973项目(2013CB329003)；通信网信息传输与分发技术重点实验室课题(EX156410046)

牛红威(1992—)，女，硕士研究生，主要研究方向：移动通信。叶 亮(1981—)，男，博士，研究员，硕士生导师，主要研究方向：移动通信、模式识别。

10. 3969/j.issn. 1003-3114. 2017.05.10

牛红威,叶亮,李卓明,等.基于WFRFT的混合载波系统资源分配算法 [J].无线电通信技术,2017,43(5):42-46.

[NIU Hongwei,YE Liang,LI Zhuoming,et al. Resource Allocation Algorithm for Hybrid Carrier System Based on WFRFT [J]. Radio Communications Technology,2017,43(5):42-46.]

TN929.5

A

1003-3114(2017)05-42-5