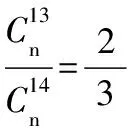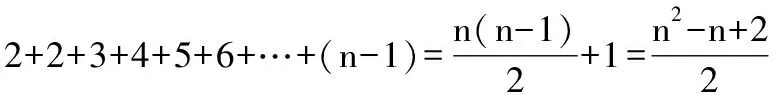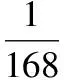题组变式训练(二)
——数学文化类高考训练题
2017-08-11山东尹承利
山东 尹承利
题组变式训练(二)
——数学文化类高考训练题

【数列】
1.《九章算术》是我国古代数学名著,其中有道“竹九节”问题:“今有竹九节,下三节容四升,上四节容三升,问中间二节欲均容各多少?”意思为:今有竹九节,下三节容量和为4升,上四节容量之和为3升,且每一节容量变化均匀(即每节容量成等差数列).问每节容量各为多少?在这个问题中,中间一节的容量为
( )
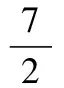
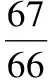
2.《九章算术》里有一段叙述:“今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢.问:几日相逢?”这道题的答案是
( )
A.12日 B.16日
C.8日 D.9日
3.(2016·河北三市第二次联考)古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺.问日几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天织了5尺布,问这女子每天分别织布多少?”根据上题的条件,若要使织布的总尺数不少于30尺,该女子所需的天数至少为
( )
A.7 B.8
C.9 D.10
4.南北朝时,在公元466—484年,张邱建写了一部算经,即《张邱建算经》,在这本算经中,张邱建对等差数列的研究有一定的贡献,例如算经中有一道题为:“今有十等人,每等一人,宫赐金以等次差降之,上三人先入,得金四斤,持出,下四人后入得金三斤,持出,中间三人未到者,亦依等次更给.”则每一等人比下一等人多得________斤金.(不作近似计算)
5.我国古代数学名著《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=
( )
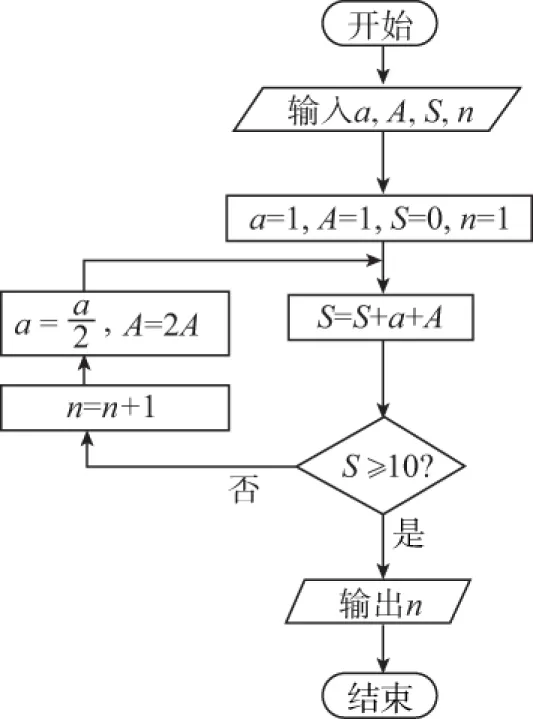
A.4 B.5 C.2 D.3
【立体几何】
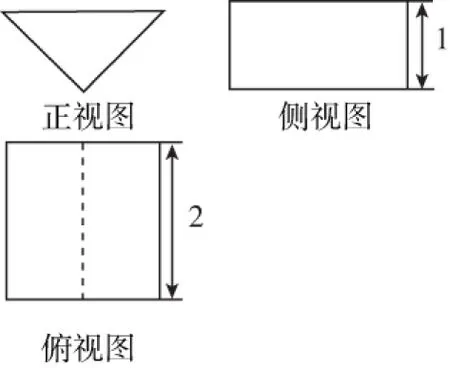
1.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的侧面积为
( )
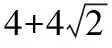
2.《九章算术》中记载了公元前344年商鞅督造一种标准量器——商鞅铜方升,其三视图如图所示(单位:寸).若π取3,其体积为12.6 (立方寸),则图中的x= ,其表面积为 .(说明:求表面积时,π不取近似值)
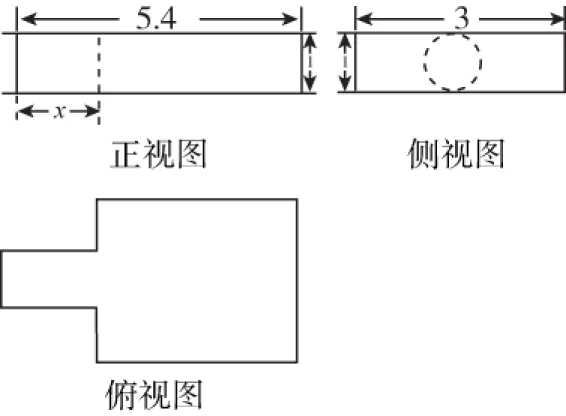
( )
A.1丈3尺
B.5丈4尺
C.9丈2尺
D.48丈6尺
4.《九章算术》是我国古代数学经典,其对勾股定理的论述比西方早一千多年.其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).
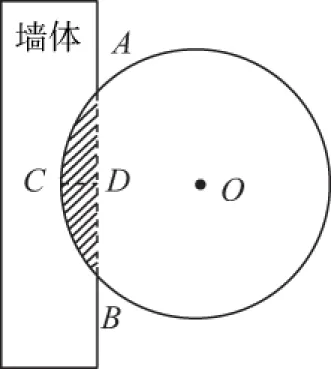
A.600立方寸
B.610立方寸
C.620立方寸
D.633立方寸
5.《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1 000多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵ABC-A1B1C1中,AC⊥BC.
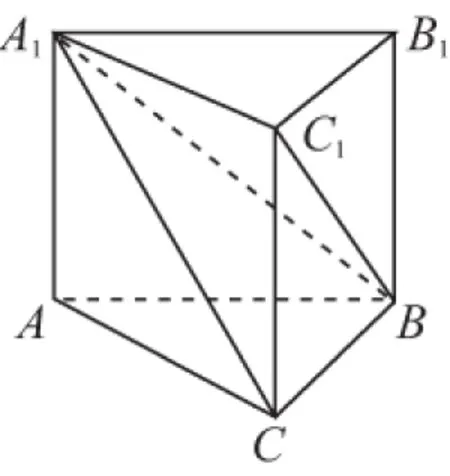
(1)求证:四棱锥B-A1ACC1为阳马,并判断四面体A1CBC1是否为鳖臑,若是写出各个面的直角(只写出结论);
(2)若A1A=AB=2,当阳马B-A1ACC1体积最大时;
①求堑堵ABC-A1B1C1的体积;
②求C到平面A1BC1的距离;
③求二面角C-A1B-C1的余弦值.
【解析几何】
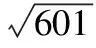
【概率统计】
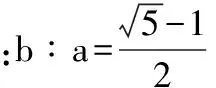
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确的结论是
( )
A.甲批次的总体平均数与标准值更接近
B.乙批次的总体平均数与标准值更接近
C.两个批次总体平均数与标准值接近程度相同
D.两个批次总体平均数与标准值接近程度不能确定
2.在下图的杨辉三角的第 行出现三个相邻的数,其比为3∶4∶5.
第0行 1
第1行 1 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
第5行 1 51010 5 1
… … …
3.如图的杨辉三角:

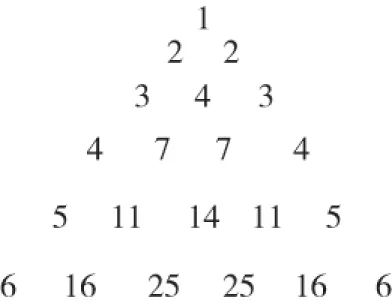
4.如图满足:(1)第n行的首尾两数均为n;(2)表中的递推关系类似杨辉三角.则第n(n≥2)行的第2个数为 .
5.按照下图中的规律,从左往右数第8行第3个数为 .

“数学文化”类高考训练题组二答案
【数列】
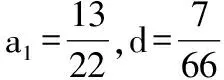
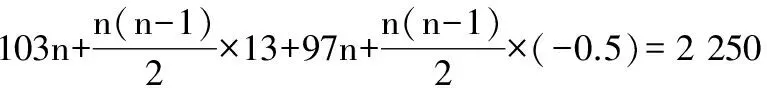
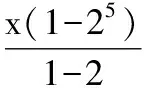
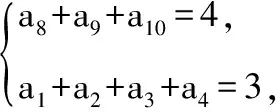
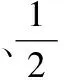
【立体几何】
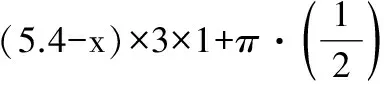
3.解:设圆柱底圆半径为R,则1.62×2 000≈3R2×13.33,解得R≈81尺.圆柱底圆周长约为2πR≈48.6.故选D.
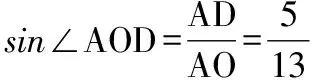
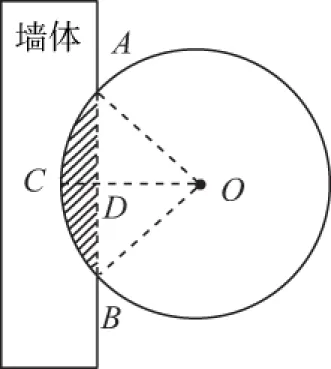
所以∠AOD=22.5°,即∠AOB=45°,
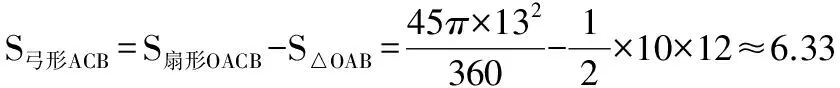
5.解:(1)证明:由堑堵ABC-A1B1C1的性质知:
四边形A1ACC1为矩形.
因为A1A⊥底面ABC,BC⊂平面ABC,
所以BC⊥A1A,
又BC⊥AC,A1A∩AC=A,A1A,AC⊂平面A1ACC1,
所以BC⊥平面A1ACC1,所以四棱锥B-A1ACC1为阳马,且四面体A1CBC1为鳖臑,四个面的直角分别是∠A1CB,∠A1C1C,∠BCC1,∠A1C1B.
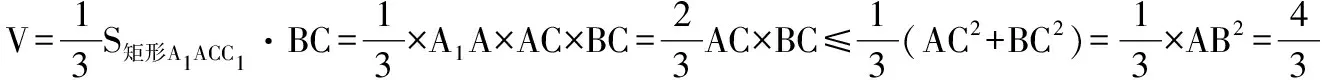
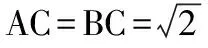
①堑堵ABC-A1B1C1的体积
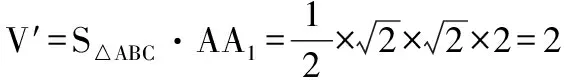
②由题意与题图知,
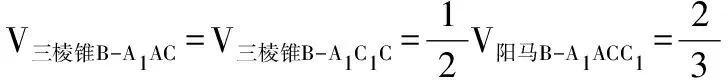
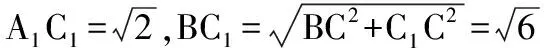
设C到平面A1BC1的距离为d,则
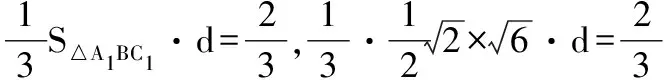
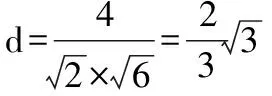
③设C在平面A1BC1上的射影为D(事实上D∈BC1).在A1B上的射影为E.
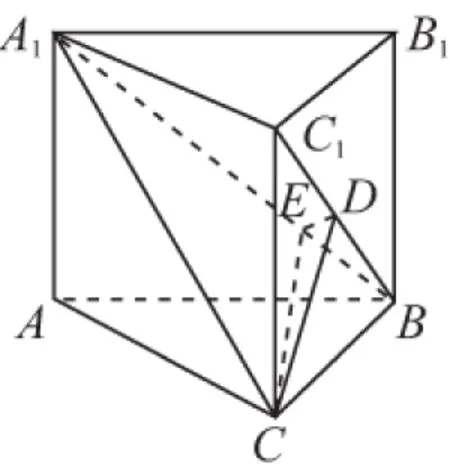
连接DE,易知A1B⊥ED.
所以∠CED即为二面角C-A1B-C1的平面角.
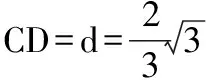
由直角三角形A1BC得
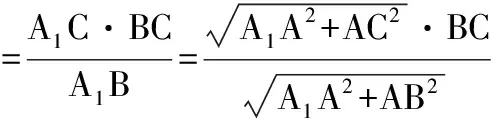

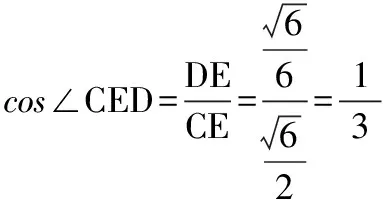
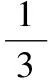
【解析几何】
1.解:设水深为x,则x2+52=(x+1)2,解得x=12.
以AB所在的直线为x轴,芦苇所在的直线为y轴,建立直角坐标系,
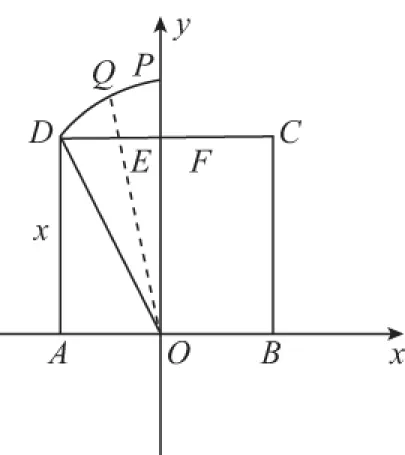
在牵引过程中,P的轨迹是以O为圆心,半径为13的圆,
其方程为x2+y2=169(-5≤x≤5,12≤y≤13),①
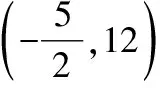
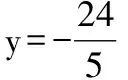
【概率统计】
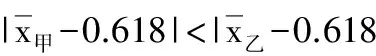
所以甲批次的总体平均数与标准值更接近.故选A.
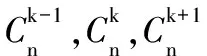
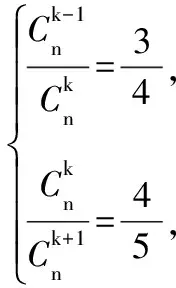
解得k=27,n=62.故在第62行出现.