基于渐进添边的准循环压缩感知时延估计算法∗
2017-08-09冷雪冬王大鸣巴斌王建辉
冷雪冬 王大鸣 巴斌 王建辉
(解放军信息工程大学信息系统工程学院,郑州 450001)
基于渐进添边的准循环压缩感知时延估计算法∗
冷雪冬†王大鸣 巴斌 王建辉
(解放军信息工程大学信息系统工程学院,郑州 450001)
(2016年12月15日收到;2017年2月3日收到修改稿)
针对时延估计问题中压缩感知类算法现有测量矩阵需要大量数据存储量的问题,提出了一种基于渐进添边的准循环压缩感知时延估计算法,实现了稀疏测量矩阵条件下接收信号时延的准确估计.该算法首先建立压缩感知与最大似然译码之间的理论桥梁,然后推导基于低密度奇偶校验码的测量矩阵的设计准则,引入渐进添边的思想构造具有准循环结构的稀疏测量矩阵,最后利用正交匹配追踪算法正确估计出时延.对本文算法的计算复杂度与测量矩阵的数据存储量进行理论分析.仿真结果表明,所提算法在测量矩阵维数相同的条件下正确重构概率高于高斯随机矩阵和随机奇偶校验测量矩阵,相比于随机奇偶校验矩阵,在数据存储量相等的条件下,以较少的计算复杂度代价得到了重构概率的较大提高.
时延估计,压缩感知,测量矩阵,渐进添边
1 引 言
时延估计[1]问题是无线定位技术[2]中备受关注的研究热点,压缩感知(compressed sensing,CS)理论[3]在2004年提出后被广泛应用于图像还原[4]、角度估计[5]中.在时延估计问题中,同样可以将信号到达时间稀疏化来构造信号的时域稀疏模型[6],从而利用CS理论对接收信号进行重构.CS理论的核心问题是信号的重构问题,针对重构算法的研究和改进一直是CS理论的研究重点,然而要提高信号的正确重构概率,仅仅研究鲁棒性强、普适性高的重构算法是不够的.由于测量矩阵在重构信号的过程中具有至关重要的作用,针对测量矩阵的研究在近两年成为该领域的研究热点.现有的测量矩阵主要分为两类,即随机测量矩阵和确定性测量矩阵.随机测量矩阵[7]包括高斯随机矩阵、托普利兹矩阵、随机伯努利矩阵、局部哈达码矩阵和局部傅里叶矩阵等.这一类测量矩阵的性能存在瓶颈:首先,由于测量矩阵的数据往往是冗余的,因此随机数的生成与存储对硬件提出了很高的要求;其次,随机矩阵只能在统计意义上以高概率满足约束等距性(restricted isometry property,RIP)准则[8],即不能确保任意一个随机矩阵都满足正确重构的必要条件.
为了解决随机测量矩阵的数据存储量冗余问题并对其性能进行确定性分析,很多新的方法被应用于确定性测量矩阵的研究之中.文献[9]中的测量矩阵从有限域出发,根据多项式的系数构造测量矩阵,在二维图像的重构过程中性能优于高斯随机矩阵.但该方法构造的测量矩阵复杂度受维度影响较大.文献[10]定义了测量矩阵的Welch界,并据此构建了最大Welch界等式矩阵,取得了较好的重构效果.但该矩阵只能在特定条件下构造,应用的普适性不高.2012年,文献[11]将测量矩阵与信道编码(channel coding,CC)理论有机地结合到一起,提出了基于低密度奇偶校验(low density parity check,LDPC)码的确定性测量矩阵,实现了稀疏测量矩阵条件下对图像的正确恢复.但在生成LDPC码测量矩阵时所采用的随机选择非零元素位置的方法,有一定概率产生具有短环结构的测量矩阵,增加迭代次数导致重构性能的鲁棒性差.文献[12,13]基于有限域生成两类LDPC测量矩阵,在图像的恢复中得到了较好的效果.但是该方法并没有考虑到LDPC码所具有的特定结构,导致构造复杂度较高.
本文提出了一种基于渐进添边(progressive edge-growth,PEG)的准循环CS时延估计算法,基于PEG思想所构造的LDPC测量矩阵不仅具有准循环结构,且对应的因子(Tanner)图中具有最大的环数.在稀疏重构的过程中利用正交匹配追踪(orthogonal matching pursuit,OMP)算法[14]得到多径时延的无偏估计.通过仿真实验将本文算法与高斯随机测量矩阵、随机LDPC测量矩阵进行对比,并对这三种测量矩阵的存储数据量以及计算复杂度进行分析,实验结果体现了本文所提出算法的优越性.
2 数学模型
2.1CS理论模型
在利用CS理论对时延进行估计的过程中,设X是长度为N的时域稀疏信号,通过线性测量后得到长度为M的观测信号Y∈RM,W表示测量误差.信号的观测向量模型为

其中HCS是测量矩阵,矩阵维度为M×N,对信号的时延进行估计的过程就是通过Y对X进行重构的过程.当W=0时,该问题是精确信号重构问题;当W̸0时,该问题为信号估计问题.由于X是稀疏信号,重构的数学表达式为

对(2)式进行求解得到接收信号的时延估计.由于(2)式的求解是一个NP-Hard[15]问题,可以将其转化为ℓ1范数的线性规划问题,

在解决(3)式的ℓ1范数问题时,常用的算法为OMP算法、基追踪(basic pursuit,BP)算法等.这类算法通过迭代来估计向量X.OMP算法的核心步骤为:在第k次迭代中,将Y正交地投影到HCS的每一列(原子)上,

挑选出Yk最大值所对应的原子存入并根据(5)式计算残差rk,如果|rk|< 10−5则迭代结束,反之迭代继续进行.迭代结束后中原子在HCS的相对位置即对应时延的估计值.

通过对现有重构算法的分析,HCS在估计过程中起至关重要的作用.无论是稀疏信号还是信号中含有噪声的伪稀疏信号,在“合适”的测量矩阵的测量下均能准确地恢复出信号.根据文献[16],“合适”的测量矩阵需要满足RIP准则、零空间性(null-space property,NSP)准则[17]等条件.由于NSP准则是正确重构的充要条件,且有助于构造与CC理论相结合的测量矩阵,下面对测量矩阵的NSP准则进行推导.
定义a为任意实向量,对于实数域R上的N列矩阵HCS,定义其R维零空间为NullspR(HCS)={a∈RN|HCS.a=0}.令S⊆ I(HCS),其中I(HCS)为HCS的列向量集合,如果对于任意非负常数C∈R≥0,零空间上所有向量v∈NullspR(HCS)都满足(6)式时,
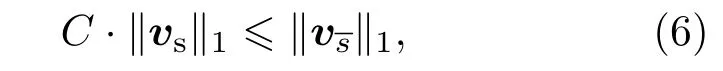
称HCS满足NSP准则,表示为HCS∈NSPR≤(S,C);当v满足(7)式时,

称HCS满足严零空间特性(strict null-space property,S-NSP)准则,表示为HCS∈NSPR<(S,C).当HCS满足NSP准则时,稀疏信号可以通过HCS成功重构.
2.2CC理论模型
在CC理论中,对于任何一个无记忆信道,假设传输码字A在有限域N2∈{0,1}上取值,接收码字为B,在传输过程中传输A接收B的概率为PB|A(B|A). 编码准则基于线性二进制码γCC,令的生成矩阵.那么A可以由GCC和信息向量ε编码产生,即A=GCC.ε(mod2).采用最大似然译码(maximum likelihood decoding,MLD),根据B对A进行译码的数学模型为
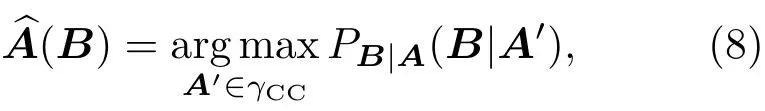

通过求解(9)式实现对传输码字的译码.在第3部分将对MLD的原理进行进一步分析,并推导出MLD与CS理论测量矩阵之间的联系.
3 基于PEG的准循环CS时延估计算法
3.1MLD与CS的理论桥梁
根据对数函数的单调性,maxPB|A(B|A′)可以转化为

定义对数函数比率为
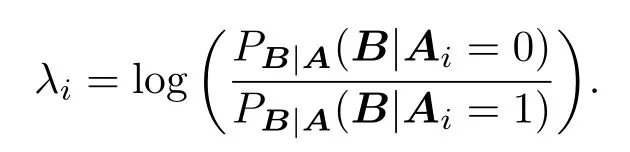
由于Ai∈{0,1},因此对数函数可以表示为

根据(10)式,(9)式可以表示为如下形式:

由于线性函数的最值点位于凸集的极值点,(11)式可以表示为
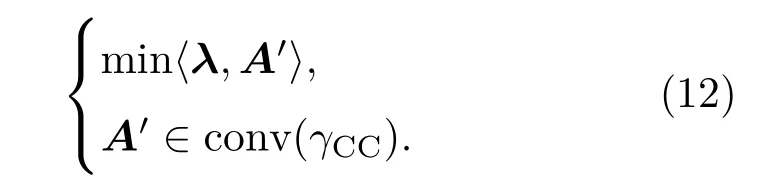
其中conv(γCC)表示γCC在Rn空间上对应的凸集.(12)式是一个线性规划问题,但是其计算复杂度随码长的增加而指数性增加.(12)式可以通过对其约束的松弛集最优化来求解,即
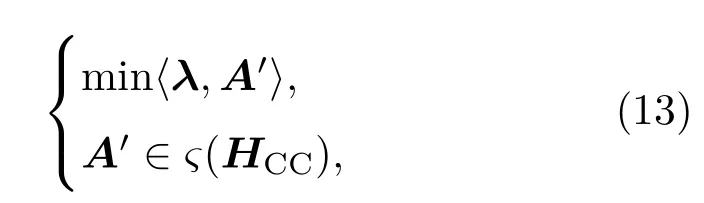
其中HCC是校验矩阵,ς(HCC)是conv(γCC)的松弛集,满足ς(HCC)⊇ conv(γCC).定义HCC的基本圆锥ψ(HCC)为满足(14)式的向量ρ的集合,

其中I(HCC)是HCC列向量的集合,J(HCC)是HCC行向量的集合.根据文献[11]可知,约束于ς(HCC)的正确译码概率等同于约束于ψ(HCC)的正确译码概率,且当ψ(HCC)中的向量ρ满足(15)式时,MLD能够正确译码,
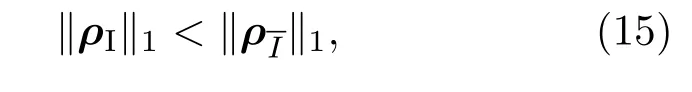
(15)式与S-NSP准则的表达式一致,即可以将MLD与CS理论联系在一起.
当HCS仅在有限域N2∈{0,1}上取值时,如果HCS满足S-NSP准则,那么HCS也满足基本圆锥正确译码的条件.因此对于任意一个给定的二进制矩阵HCS,当HCS在MLD中具有较好的性能时,将HCS作为测量矩阵对信号进行重构也同样具有着极好的性能,CS理论与MLD的理论桥梁如图1所示.LDPC矩阵已经被证明在CC模型中具有能够逼近香农限的性能,因此基于LDPC码对测量矩阵进行确定性构建能够提高正确重构出时延的概率.

图1 CS与MLD的理论连接桥梁图Fig.1.The theoretical bridge graph between the CS theory and the MLD theory.
3.2基于LDPC码的测量矩阵设计准则
LDPC码是一类具有线性码特性的分组码,定义码长为n的LDPC码的监督矩阵满足每行的非零元素,即行重为ωi,每一列的非零元素,即列重为ωj,这一类码可以称为(n,ωj,ωi)规则低密度校验码.由于其校验矩阵中仅包含少量的非零项,即LDPC码具有稀疏性.例如一个(8,2,4)的LDPC码监督矩阵如(16)式所示:
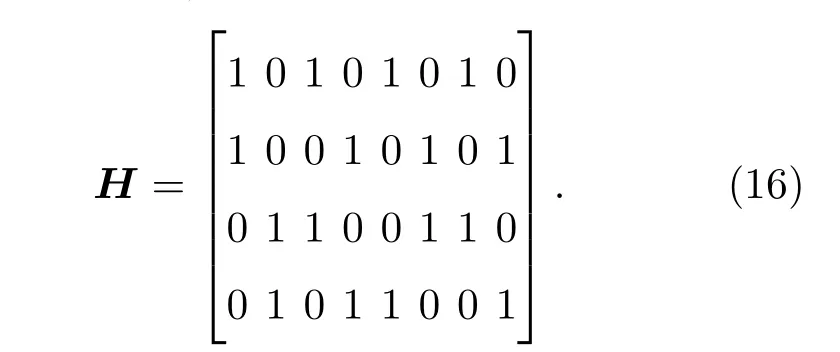
H的每一列具有2个非零向量,每一行具有4个非零向量,根据(16)式可知其对应的监督方程为

将这四个监督方程的约束关系分别记为Z1,Z2,Z3,Z4,码元的约束关系可以表示为LDPC码的Tanner图,如图2所示.

图2 (8,2,4)的规则LDPC码的因子图Fig.2.Tanner graph of the regular(8,2,4)LDPC code.
图2中,实心节点称为校验节点,与监督方程的约束关系相对应,空心节点称为变量节点,与LDPC码的码元相对应.变量节点与校验节点的连线表示在监督方程的第i个约束关系Zi中包含LDPC码中第j个码元xj.如果从一个节点出发,不经过重复的路线,能回到起始节点,则所经过的节点与路线可以构成一个环,其中连线的数目即环的长度.如Z1→x2→Z3→x6→Z1是一个长度为4的环.Tanner图不但是研究LDPC码的一个重要工具,而且是一个重要的性能指标.在稀疏重构的过程中,采用LDPC码测量矩阵对信号正确重构的前提是节点之间传递信息统计独立,而当LDPC码的Tanner图中有环存在时,意味着从某一节点发送的信息经过环回路的传递后回到发送节点,导致了发送节点信息的叠加,影响了重构的准确性.然而对于有限长度的测量矩阵而言,其LDPC码的长度是有限的,环的存在必不可少,而短环的存在更会增加迭代次数,导致重构性能差.因此在设计过程中,在给定测量矩阵维度的情况下,应基于环数最大的原则设计基于LDPC码的测量矩阵.
3.3基于PEG思想的准循环LDPC测量矩阵的构造
文献[18]中首次利用随机构造的LDPC码监督矩阵作为测量矩阵,实现了接收信号角度的正确重构,该方法构建的测量矩阵虽然具有稀疏特性,降低了存储空间,但是码长趋近于无穷大,因此通常仅具有理论分析意义,而且随机构造的LDPC码由于其结构不可控制,有一定概率生成存在短环结构的测量矩阵,从而导致不能精确重构出信号.
本文针对此问题进行改进,首先引入PEG算法的思想,通过展开Tanner图,连接距离最远的变量节点和校验节点的方式,令Tanner图的环数最大化,构造出环数最大的基矩阵;然后基于循环结构对基矩阵进行扩展,得到具有准循环结构的LDPC码测量矩阵.
本文构造矩阵维度为M×N,列重为ωj的测量矩阵的步骤为:
2)任意选择一个变量节点xj,连接Tanner图中连线最少的校验节点Zi,将这条连线称为xj的边,记做
3)为xj添加其他边,以xj为父节点将Tanner图展开到深度l,如果其扩展树上第l层校验节点集合且第l+1层校验节点的补集则将xj与中连线最少的校验节点相连;
4)重复步骤3,添加完毕所有与xj相连的边集合;
5)重复步骤2—4,添加完毕所有变量节点集合X={x0,x1,...,xt−1},构造出维度为c×t的基矩阵Q,其中Q中1代表非零循环子矩阵,0代表全零矩阵;
6)根据Q和(18)式计算Q中每个元素的循环移位次数矩阵P,

其中z表示每一行中第z+1个“1”元素出现的相对位置,pij={0,1,...,L−1,∞}表示将矩阵R的每一行向右移位pij位,移位后得到循环置换矩阵;
7)根据矩阵Q和P,用循环置换矩阵和全零矩阵分别代替Q中的“1”元素和“0”元素,扩展后得到测量矩阵HCS.
3.4基于PEG的准循环CS时延估计算法步骤
根据上述推导,可以将稀疏重构时延估计问题中基于矩阵循环群LDPC码的估计算法归纳为如下步骤:
1)利用3.3节中的设计算法构造循环LDPC码测量矩阵HCS;
2)通过测量矩阵得到接收信号Y,利用2.1节中的OMP算法,根据(4)式,经过k次迭代选取原子;
3)根据HCS与τ的对应关系得到时延估计值
4 仿真实验
本文研究的是CS类时延估计算法,为验证本文算法的实用性与鲁棒性,采用蒙特卡罗实验将本文算法与高斯随机测量矩阵和随机LDPC测量矩阵进行对比分析.
仿真一假设接收信号的Lp=5,到达时间分别为 τ1=200 ns, τ2=400 ns, τ3=600 ns,τ4=800 ns,τ5=1000 ns,分别在SNR=10和0 dB的条件下采用本文算法进行m=200的仿真实验.其中测量矩阵维度为64×512,列重ωj=8,得到时延的估计值,如图3(a)和图3(b)所示.可以看出本文算法在稀疏测量矩阵的条件下能够得到时延的无偏估计,如图3(a)所示.且在低信噪比(SNR=0 dB)条件下,根据第三条径的局部放大图可以看出本文算法依旧能够正确估计出时延,如图3(b)所示,对于噪声具有较好的鲁棒性.

图3 不同信噪比条件下五条径的时延估计值分布图(a)SNR=10 dB条件下本文算法五条径的时延估计值;(b)SNR=0 dB条件下本文算法五条径的时延估计值(内插图为第三条径时延估计值的局部放大图)Fig.3.Distribution of time delay estimation of 5 path under di ff erent SNR conditions:(a)Time delay estimation of 5 path under the condition of SNR=10 dB by the algorithm in this paper;(b)time delay estimation of 5 path under the condition of SNR=0 dB by the algorithm in this paper(the interior illustration is the local magni fi cation for time delay estimation of the third path).
仿真二在测量矩阵维度相同(维度为64×512),SNR=10 dB的条件下,将本文算法与高斯随机测量矩阵和随机LDPC测量矩阵进行对比,分别绘制这三种算法的正确重构概率随多径数目变化的曲线,结果如图4所示.可以看出,当Lp≤8时,三种算法的正确重构概率没有区别,当Lp>8时,本文算法与随机LDPC测量矩阵的正确重构概率高于高斯随机测量矩阵.本文算法由于引入PEG算法的思想,相比于随机LDPC测量矩阵减少了Tanner图中短环的数量,因此在Lp较大时,具有更胜一筹的性能.
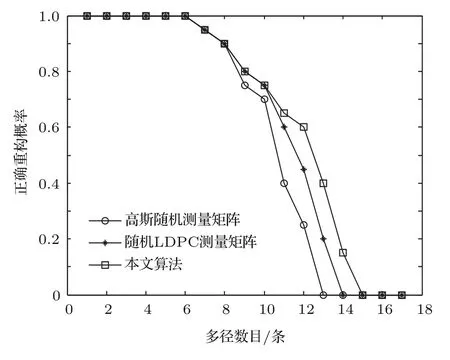
图4 不同算法正确重构概率随多径数目变化对比图Fig.4.The variation of the probability of correct reconstruction with the number of multipath contrast of di ff erent algorithms.
仿真三在不同测量矩阵维度,SNR=10dB的条件下进行仿真,分别绘制本文算法在维度为64×512,64×1024,128×1024时正确重构概率随多径数目变化的曲线,仿真结果如图5所示.可以看出在仿真条件一定的条件下,128×1024维的测量矩阵有着最好的重构效果.因此正确重构概率的下降过程随测量矩阵维度的增加而滞后.
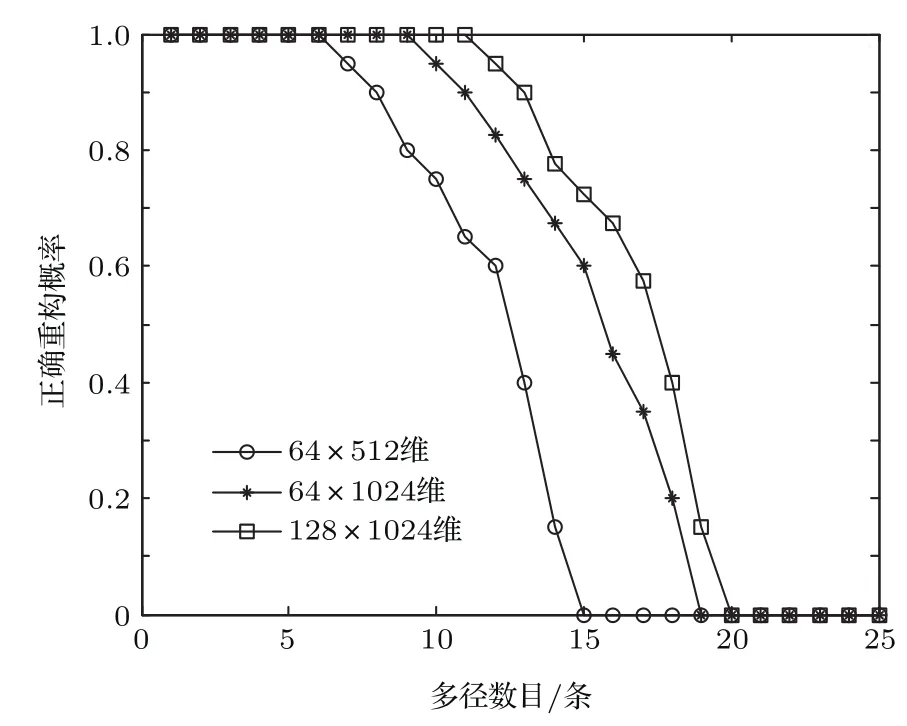
图5 不同矩阵维度条件下本文算法正确重构概率随多径数目变化对比图Fig.5.The variation of the probability of correct reconstruction with the number of multipath contrast of di ff erent matrix dimensions.
仿真四在矩阵维度为64×512,SNR=10 dB的条件下,根据(19)式,计算本文算法中测量矩阵的相关值.

其中‖.‖2为向量的ℓ2范数.本文算法中测量矩阵的相关值随列重的变化如图6所示,可以看出相关值随列重的增加而减小.根据文献[19],可知测量矩阵相关值越小,重构精度越高.根据表1可知列重的增加会导致存储空间与计算复杂度的增加,因此为平衡重构精度与存储空间及计算复杂度之间的关系,本文算法中测量矩阵的列重取值设置为8.
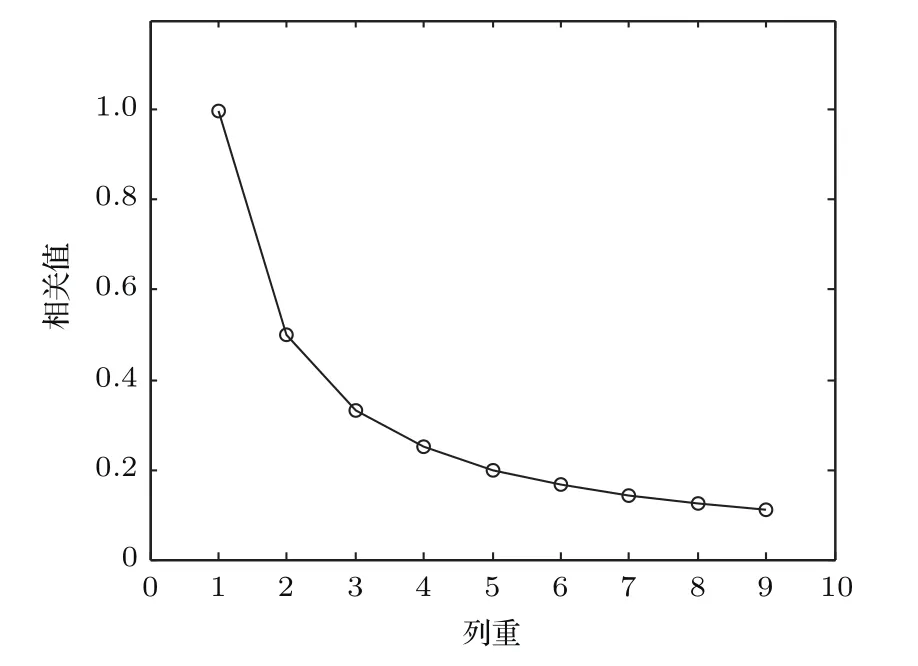
图6 本文算法测量矩阵相关值随列重变化示意图Fig.6.The variation of the measurement matrix correlation value with the column weight of the algorithm in this paper.
5 存储空间与计算复杂度分析
假设测量矩阵的维度为M×N,随机LDPC测量矩阵与本文测量矩阵的列重均为ωj.由于高斯随机测量矩阵中的每个元素均为随机数,因此高斯随机测量矩阵的存储空间为M×N,LDPC类测量矩阵的每行仅有ωj个元素取值为1,其余元素为0,因此LDPC类测量矩阵的存储空间为N×ωj.
在采用CS算法估计时延的过程中,计算复杂度分成两部分,即测量矩阵的生成与信号的重构.在采用OMP算法重构信号的过程中,计算复杂度主要包括两部分:计算相关值u,复杂度为O(MN);更新余量,复杂度为O(3M+2),为正确重构全部时延,算法需经过Lp次迭代.高斯随机测量矩阵只需要生成维度为M×N的随机数,因此算法复杂度为

由于随机LDPC测量矩阵在生成过程中,在每一列随机选取ωj个非零元素,因此算法复杂度为
生成测量矩阵的复杂度为O(2ct+2).

表1列出了三种算法计算复杂度与存储空间的对比.本文算法相比于高斯随机测量矩阵降低了存储空间,与随机LDPC测量矩阵相比,在存储空间相同的条件下,以较小复杂度的代价得到了性能的较大提升.

表1 算法计算复杂度与存储空间对比表Table 1.The comparison of the algorithm complexity and storage space.
6 结 论
在时延估计问题中,现有基于LDPC码的测量矩阵具有在少量数据存储量的条件下较好的估计性能,但在测量矩阵的生成过程中,由于随机选择非零元素位置,导致Tanner图中短环的出现,影响重构效果.针对该问题,本文首先引入了PEG算法有效减少了Tanner图中短环的存在,然后基于准循环结构构造测量矩阵,实现了少量数据量条件下无偏时延估计.在相同多径数目的条件下比高斯随机测量矩阵和随机LDPC测量矩阵正确重构概率更高.同时给出了数据存储量与计算复杂度分析,仿真结果表明该算法性能优越、稳定可靠.
[1]Zhang Q F,Huang J G,Xie Y Q 1995Acta Acust.20 211(in Chinese)[张群飞,黄建国,谢一清 1995声学学报20 211]
[2]Li J 2011Electron.Meas.Technol.34 73(in Chinese)[李剑 2011电子测量技术 34 73]
[3]Donoho D L 2006IEEE Trans.Inform.Theory52 1289
[4]Ning F L,He B J,Wei J 2013Acta Phys.Sin.62 174212(in Chinese)[宁方立,何碧静,韦娟 2013物理学报 62 174212]
[5]Shen Z B,Dong C X,Huang L,Zhao G Q 2014J.Electron.Inform.Technol.36 2935(in Chinese)[沈志博,董春曦,黄龙,赵国庆2014电子与信息学报36 2935]
[6]Leng X D,Ba B,Lu Z Y,Wang D M 2016Acta Phys.Sin.65 210701(in Chinese)[冷雪冬,巴斌,逯志宇,王大鸣2016物理学报65 210701]
[7]Wang Q,Li J,Shen Y 2013Acta Electron.Sin.41 2041(in Chinese)[王强,李佳,沈毅2013电子学报 41 2041]
[8]Candes E J,Tao T 2005IEEE Trans.Inform.Theory51 4203
[9]DeVore R A 2007J.Complexity23 918
[10]Xia P F,Zhou S L,Giannakis G B 2005IEEE Trans.Inform.Theory51 1900
[11]Dimakis A G,Smarandache R,Vontobel P O 2012IEEE Trans.Inform.Theory58 3093
[12]Xia S T,Liu X J,Jiang Y 2015IEEE Trans.Signal Process.63 1017
[13]Mohades A,Tadaion A A 2016IET Signal Process10 168
[14]Elad M 2008IEEE Trans.Signal Process.55 5695
[15]Hochba D S 1997ACM Sigact News28 40
[16]Tillmann A M,Pfetsch M E 2014IEEE Trans.Inform.Theory60 1248
[17]Gao Y,Peng J G,Yue S G,Zhao Y 2015J.Function Spaces205 579853
[18]Sun J M 2016Modern Radar38 46(in Chinese)[孙晶明2016现代雷达38 46]
[19]Dang K,Ma L H,Tian Y,Zhang H W,Ru L,Li X B 2015J.Xidian Univ.42 186(in Chinese)[党骙,马林华,田雨,张海威,茹乐,李小蓓 2015西安电子科技大学学报(自然科学版)42 186]
PACS:07.50.Qx,07.05.Kf,84.40.Ua,89.70.EgDOI:10.7498/aps.66.090703
A quasi-cyclic compressed sensing delay estimation algorithm based on progressive edge-growth∗
Leng Xue-Dong†Wang Da-Ming Ba Bin Wang Jian-Hui
(The PLA Information Engineering University,Zhengzhou 450001,China)
15 December 2016;revised manuscript
3 February 2017)
Time delay estimation(TDE)is a hot research topic in wireless location technology.Compressed sensing(CS)theory has been widely applied to image reconstruction and direction of arrival estimation since it was proposed in 2004.The sparse model can be constructed in time domain for estimating the time delay by using the CS theory.The measurement matrix plays a crucial role in the processing of signal reconstruction which is the core problem of CS theory.Therefore the research in the measurement matrix has becomes a hotspot in recent years.The existing measurement matrix is mainly divided into two categories,i.e.,random measurement matrix and deterministic measurement matrix.The performance of random measurement matrix has bottlenecks.Firstly,because of the redundant measurement matrix data,the generation and storage of the random number put forward a high requirement for hardware.Secondly the random matrix can only satisfy the restricted isometry property in a statistical sense.The research of the deterministic measurement matrix is of great value under this background.The parity check matrix of low density parity check(LDPC)code has good performance in CS theory.However,the method of randomly selecting non-zero element position has a certain probability to generate a measurement matrix with a short loop structure during generating LDPC code measurement matrix.The robustness of the reconstruction performance decreases with the increase of iteration times.
A novel quasi-cyclic CS algorithm based on progressive edge-growth is constructed to estimate the time delay.The purpose of this article is to deal with the need to store a large number of data in existing measurement matrix during time delay,by using the CS theory.The algorithm presented here can achieve TDE in a high precision.First,the theoretical bridge between CS and the maximum likelihood decoding is established.And the design criterion of measurement matrix based on the LDPC code is derived.The sparse measurement matrix with quasi-cyclic structure is constructed by introducing the idea of progressive edge-growth.Finally,the orthogonal matching pursuit algorithm is used to estimate the time delay.Furthermore,the computational complexity of the algorithm and the data storage of the measurement matrix are analyzed theoretically.Simulations show that the correct reconstruction probability of the proposed approach is higher than those of the Gauss random matrix and random LDPC matrix under the same dimension.Compared with the random LDPC matrix,the proposed method can improve performance at the expense of less complexity under the condition of the same data storage.
time delay estimation,compressed sensing,measurement matrix,progressive edge-growth
10.7498/aps.66.090703
∗国家自然科学基金(批准号:61401513)资助的课题.
†通信作者.E-mail:lengxuedong@outlook.com
*Project supported by the National Natural Science Foundation of China(Grant No.61401513).
†Corresponding author.E-mail:lengxuedong@outlook.com
