点光源哈特曼最优阈值估计方法研究

周睿 魏凌李新阳王彩霞李梅沈锋

1)(中国科学院自适应光学重点实验室,成都 610209)2)(中国科学院光电技术研究所,成都 610209)3)(中国科学院大学,北京 100049)

点光源哈特曼最优阈值估计方法研究

周睿1)2)3)†魏凌1)2)李新阳1)2)王彩霞1)2)李梅1)2)沈锋1)2)

1)(中国科学院自适应光学重点实验室,成都 610209)2)(中国科学院光电技术研究所,成都 610209)3)(中国科学院大学,北京 100049)

(2016年11月8日收到;2017年2月4日收到修改稿)

针对夏克-哈特曼波前传感器探测系统中噪声随时间及空间变化频率较快的特点,为了准确估计系统的最优阈值,根据高斯光斑与噪声的分布特性,提出一种以滑动窗口内像素均值及图像信号的局部梯度作为参数,构造关于噪声权重函数的方法,由此获得子孔径阈值的最优估计值,并详细分析了算法的基本原理和实现过程.以典型处理方法获取的阈值与理论最优阈值的误差作为评价标准,仿真和实验结果表明本文提出的阈值估计方法在不同信噪比、不同光斑大小的条件下,均能取得优于典型阈值处理方法获得的结果,且与理论最优阈值的误差小于10%.

夏克-哈特曼波前传感器,高斯光斑,最优阈值,权重函数

1 引 言

夏克-哈特曼波前传感器(SHWFS)是一种基于波前斜率测量的光学检测装置,因其具有结构简单、环境适应能力强、实时性强等优点,广泛应用于自适应光学、激光波前检验、生物光学、光学检测和装调等领域［1].SHWFS主要由微透镜阵列和电荷耦合器件(CCD)探测器组成,利用微透镜阵列对输入光束进行分割采样,每个透镜作为一个子孔径,将光束聚焦成一个光斑阵列,子孔径范围内的波前畸变将造成光斑的位置偏移,SHWFS对输入波前的测量精度主要取决于各个子孔径光斑中心位置的提取精度［2−4].光斑中心位置提取的算法有很多种,包括一阶矩法、高斯拟合法、权重法、相关法等,其中一阶矩法由于算法简单,鲁棒性强,精度较高而被广泛使用.一阶矩法以光斑强度为权重,计算区域内所有像素对光斑质心的贡献,直接得到强度分布与空间平均相位的关系［5].

然而一阶矩法对系统噪声比较敏感,为了提高一阶矩法质心提取精度,通常需要对CCD的读出信号进行预处理［6,7].在预处理的方法中,阈值处理的方法由于能够快速去除噪声的影响而受到广泛的关注［8].文献[9]指出,根据SHWFS的特点和噪声分布特性,存在一个最优阈值,使得质心的探测误差最小;同时推导了最优阈值等于噪声的均值与噪声的3倍标准差之和.然而在实际工作过程中,由于SHWFS系统中有效信号和噪声很难被区分,因此最优阈值难以实时地准确估计.

目前,获取SHWFS阈值的方法通常有基于灰度直方图统计的经验值法、迭代法、最大类间方差(Ostu)法、基于图像局部特征的阈值方法等.文献[10]提出的基于灰度直方图统计的经验值法,仅适用于噪声随时间、空间频率变化缓慢的情况,对于背景随时间、空间频率变化比较剧烈且需要对SHWFS的采样数据实时闭环的场景不适合.文献[11]指出,Ostu法在信号相对面积占图像总面积达到30%以上时其分割性能接近最优值.然而,通常情况下SHWFS波前探测系统有效信号的面积小于图像总面积的20%,采用这种方法得到的阈值偏大,从而影响质心计算的精度.文献[12,13]提出使用最大值的百分比作为阈值,但是由于百分比的确定与探测系统的信噪比(SNR)有关,在实际系统中,难以实现对百分比的优化.文献[14]提出,根据SHWFS的特点,利用探测靶面的四个边角区域估计噪声的均值和方差,这种方法只适用于背景噪声空间分布比较均匀的情况,对于背景空间分布不均匀的场合,这种为所有子孔径设置同一阈值的方法不适用.

本文针对SHWFS系统中光斑及噪声分布的特点,通过求取子孔径滑动窗口内像素均值及信号的局部梯度方向,构造噪声权重函数的方法对最优阈值进行估计,对该算法进行了仿真和实验,并将该算法得到的阈值与典型处理方法得到的阈值进行了对比和分析.结果表明,本文提出的方法与典型方法相比,能够得到更接近理论最优阈值的结果,从而有效地提高了SHWFS质心探测精度.

2 最优阈值估计方法分析

在SHWFS探测波前相位畸变时,采用孔径分割的方法,将相位面分割为多个子孔径,探测子孔径的平均斜率来重构相位.通常子孔径内的光斑强度可以用高斯函数来拟合［15],其表达式为

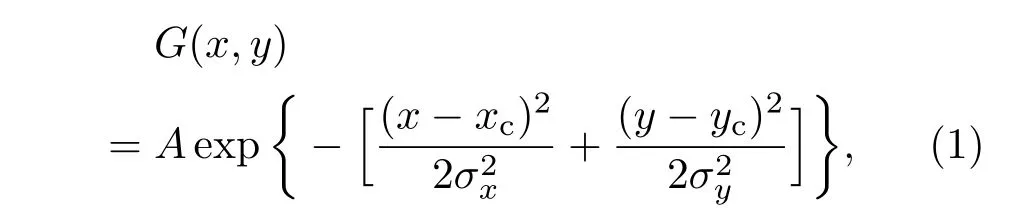
其中A为高斯光斑的幅值;xc,yc,σx,σy分别为光斑x,y方向的中心位置及x,y方向的光斑宽度.由于SHWFS光斑的强度呈高斯分布且面积较小,其像素灰度值比较集中、分散性小,而噪声一般可认为是高斯白噪声,典型SHWFS光斑沿x轴的剖面如图1所示.根据噪声和光斑的分布特性,由噪声区域对应的窗口(i)和有效光斑区域对应的窗口(ii)可以看出,随着滑动窗口逐渐靠近有效光斑的中心位置,对应窗口内像素拟合曲线与x轴的夹角、窗口内像素均值均呈现单调增长的趋势,即像素属于噪声的概率与滑动窗口内像素拟合曲线与x轴夹角及窗口内像素均值成反比.

同样,利用上述分析方法,可以对二维SHWFS光斑进行二维滑动窗口的处理,对二维滑动窗口内像素求取局部梯度方向,具体做法是对窗口内的像素信号进行平面拟合,从而得到其拟合平面法线方程与z轴的夹角,其数学过程可以表达为

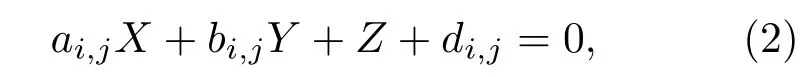
其中X,Y为光斑在滑动窗口内的坐标位置,Z为光斑强度信息,(ai,j,bi,j,di,j)T为需要求取的拟合平面法向量方程的参数,其矩阵乘法表达式为

以滑动窗口为3×3为例,可以得到

其中M,v,Z分别为滑动窗口内坐标位置组成的矩阵、待拟合平面的法向量及窗口内像素的强度向量;M+为M的伪逆.对于3×3的窗口,可以得到

因此,滑动窗口内各像素拟合平面的法向量可以表达为如下的卷积形式,其中⊗表示卷积:

图1 典型高斯光斑x轴剖面图Fig.1.The x axis pro fi le of tradition SHWFS spot.

由此,可以得到子孔径内各像素拟合平面法向量与z轴的夹角,即局部梯度方向可以表示为

同时,由前述分析可知,像素属于有效光斑的概率不仅与滑动窗口内像素拟合曲线与x轴的夹角有关,也与窗口内像素均值有关,滑动窗口内像素均值可以表示为(11)式,其归一化的均值可以表示为(12)式:

由此,像素属于噪声的概率Pi,j可以表示为θi,j,µ′i,j的权重函数,即

在上述分析的基础上,根据(13)式可得子孔径内所有像素的概率,从而得到基于滑动窗口统计的噪声均值如(15)式:

同时,为了有效估计噪声的标准差,需要将滑动窗口投影到x,y平面以便实现对有效高斯光斑区域的噪声标准差的估计,如(16)式所示,其中Z′表示去除倾斜后的光强:

由此,可以求得去除倾斜后滑动窗口中心像素的标准差估计如(17)式所示,其中分别为去除倾斜后滑动窗口各个像素的灰度值和均值,

因此,可以得到子孔径内关于噪声标准差的估计如下:

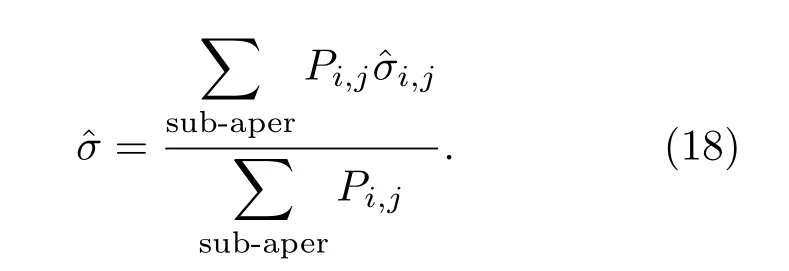
根据上述分析,由(15)和(18)式得到了子孔径内关于噪声的均值与标准差的估计值,从而可以得到子孔径内最优阈值的估计为

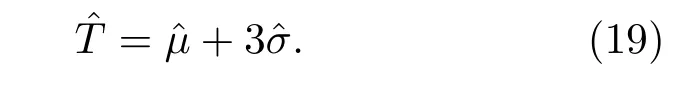
3 仿真计算及分析

为了验证基于滑动窗口投影最优阈值估计方法的有效性,本节针对该方法与迭代阈值法、最大值百分比阈值法及Ostu法求得的阈值与理论最优阈值进行了对比分析.其中迭代阈值法设定图像最大、最小灰度值的平均数为初始阈值T0,阈值T(i)将图像分为前景和后景,u,v分别为前景和后景的平均灰度等级,取T(i+1)=(u+v)/2,当迭代到T(i+1)=T(i)时停止,取该值为子孔径内图像的阈值;最大值百分比阈值法设定子孔径内图像最大值的百分比作为阈值,根据文献[12,13]通常选择最大值的30%;Ostu法将图像分为背景和目标两类,使得两类之间的方差最大,从而求得阈值.

为了便于分析和比较在不同光斑大小、不同高斯光斑中心强度及不同噪声水平情况下几种阈值处理方法结果与理论最优阈值的接近程度,可以将SNR定义为高斯光斑的能量与噪声标准差的比值,其表达式如下:

同时为了评价不同方法得到的阈值与理论最优阈值的接近程度,定义如下式所示的性能指标来衡量各种阈值处理方法的效果,

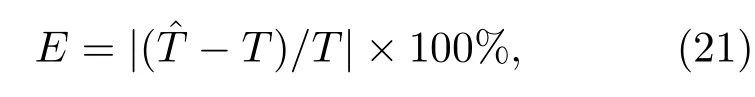
根据(1)式定义的高斯光斑,针对子孔径尺寸为24 pixels×24 pixels,高斯光斑的半径从0.5 pixels到3 pixels变化,分别利用高斯光斑能量保持不变、改变噪声水平的方法和噪声水平不变、改变高斯光斑能量的方法,在不同SNR条件下,将典型阈值处理方法与本文提出的方法进行了比较和分析.如(20)式所示,随着SNR的增加,被测光斑的质量逐渐改善.仿真过程中的典型光斑如图2所示,其中图2(a)表示在SNR=16.73 dB条件下光斑和噪声强度的分布情况,图2(b)表示受噪声影响光斑强度的三维分布情况.

当滑动窗口大小为3 pixels×3 pixels时,保持噪声水平不变,通过调整高斯光斑能量的方法改变SNR,将本文提出的最优阈值估计法、迭代阈值法、最大值百分比阈值法及Ostu法的结果与理论最优阈值进行比较,结果如图3所示.其中图3(a)—(d)表示光斑的半径σA=0.5,1.0,2.0,3.0 pixels条件下的仿真结果.从图3可以看出:在4种不同高斯光斑大小条件下,当SNR较高时,典型阈值处理方法得到的阈值约为最优阈值的2—10倍,远远高于理论的最优阈值;并且光斑半径越小,使用典型阈值处理方法得到的阈值偏离理论最优阈值的幅度越大;随着SNR的降低,典型阈值处理方法得到的阈值偏离理论最优阈值的程度有所降低,但与理论的最优阈值相比,仍有较大误差;在SNR较低的情况下,典型阈值处理方法得到的阈值会小于理论的最优阈值,并且光斑半径越大,使用典型阈值处理方法得到的阈值偏离理论最优阈值的幅度越大,最大偏差约是理论最优阈值的1/2,因此不能有效抑制噪声信号;然而,在不同的光斑大小及SNR条件下,本文提出的阈值估计方法的结果与理论最优阈值的误差均能保持在10%以内,且在各种光斑半径下一致性较好,明显优于典型阈值处理方法.

图4显示了在滑动窗口大小为3 pixels×3 pixels,保持高斯光斑能量不变,通过调整噪声水平的方法改变SNR时,本文提出的最优阈值估计法与典型阈值处理方法进行比较的结果.从图4结果可以得到与图3相同的结论:在SNR较好的情况下,典型阈值处理方法得到的阈值远远高于理论的最优阈值,在SNR较低的情况下,典型阈值处理方法得到的阈值低于理论的最优阈值;而本文提出的方法能够在不同SNR条件下,对4种高斯半径光斑得到的最优阈值与理论最优阈值的误差范围保持在10%以内.

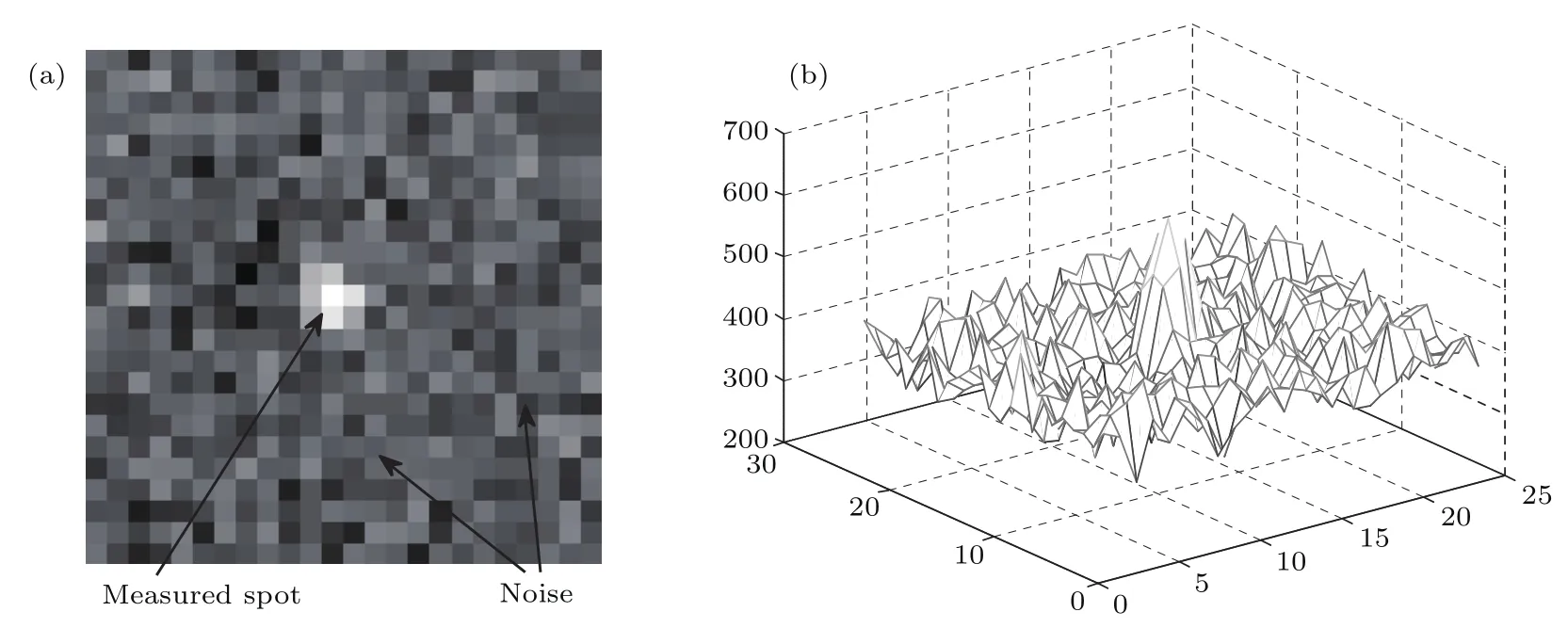
图2 (a)SNR=16.73 dB时包含背景噪声的光斑图像;(b)SNR=16.73 dB时包含背景噪声的光斑图像的三维显示Fig.2.(a)Spot image with background noise(SNR=16.73 dB);(b)the three-dimensional show of the spot image with background noise(SNR=16.73 dB).

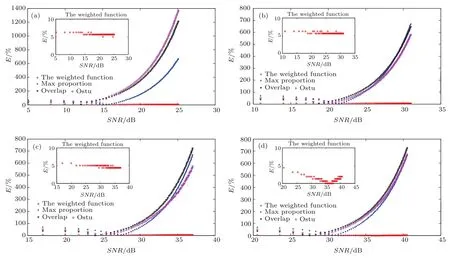
图3 (网刊彩色)噪声水平不变,不同高斯光斑强度条件下各种阈值估计方法得到的阈值与理论最优阈值的误差(a)σA=0.5;(b)σA=1.0;(c)σA=2.0;(d)σA=3.0Fig.3.(color online)The error between the theoretic threshold and the threshold obtained by di ff erent methods with the invariable noise level and the di ff erent spot energies:(a) σA=0.5;(b) σA=1.0;(c)σA=2.0;(d)σA=3.0.

图4 (网刊彩色)高斯光斑能量不变,不同噪声水平条件下各种阈值估计方法得到的阈值与理论最优阈值的误差(a)σA=0.5;(b)σA=1.0;(c)σA=2.0;(d)σA=3.0Fig.4.(color online)The error between the theoretic threshold and the threshold obtained by di ff erent methods with the invariable spot energy and the di ff erent noise levels:(a)σA=0.5;(b)σA=1.0;(c)σA=2.0;(d)σA=3.0.

从上述仿真和分析可以看出,在高斯光斑强度或噪声水平发生变化引起SNR发生改变时,本文提出的最优阈值估计方法与典型阈值处理方法相比,均能够较为准确地得到噪声的理论最优阈值.同时,本文也对不同滑动窗口大小情况下,噪声权重函数中µ′和cosθ取不同的幂指数进行了仿真和分析,均能获得与图3和图4相类似的结论.

4 实验结果

为了验证本文提出的最优阈值估计算法的效果,建立了如图5所示的实验系统.该实验系统主要包括激光器、由微透镜阵列和CCD探测器组成的SHWFS及计算处理模块3个部分.其中激光器采用波长λ=1.064µm的电流可调节的激光器,SHWFS采用方形排布8×8的微透镜阵列,单个微透镜的口径为2.667 mm,焦距为77 mm,SHWFS使用的CCD探测器靶面大小为240 pixels×240 pixels,每个子孔径大小为24 pixels×24 pixels,像元尺寸为24µm,探测器位数为14位.SHWFS获取的典型的8×8(其中有效子孔径数为48)的子光斑图像阵列如图6(a)所示,利用本文提出的最优阈值估计方法处理后的子光斑图像阵列如图6(b),各个子孔径的SNR如图6(c)所示.由图6(b)和图6(c)可以看出,在各子孔径内SNR从10—25 dB大范围波动的情况下,利用本文提出的方法依然能够有效地去除各个子孔径内的噪声.

图5 实验装置示意图Fig.5.The schematic diagram of experiment Setup.

针对如图5所示的SHWFS系统,根据文献[8,16]在光子噪声可以被忽略的情况下,将背景噪声、读出噪声、杂散光噪声等信号统一地看作是系统的探测噪声,并且该噪声服从高斯分布.首先在关闭激光器的状态下,获取SHWFS系统的噪声图像信息,通过多帧平均的方法获得相对准确的噪声均值和标准差;在实验过程中探测器的增益、曝光时间以及实验环境等条件均保持一致.因此,可以认为噪声的均值和标准差基本保持不变,即理论最优阈值保持不变,根据(19)式可以得到该实验条件下的理论最优阈值为410 ADU;然后通过调节激光器电流的方法改变有效信号的能量,从而得到受噪声影响的图像信号.对SHWFS系统采集的图像信号,分别利用本文提出的方法、迭代阈值法、最大值百分比阈值法及Ostu法求得阈值,并与理论最优阈值进行了对比分析,4种方法结果与理论最优阈值的误差曲线如图7所示;表1显示了4种方法在不同SNR条件下得到的计算结果.由图7和表1可以看出,与典型阈值处理方法相比,利用本文提出的最优阈值估计方法得到的阈值能获得更高精度最优阈值的估计值,在各种SNR条件下,与理论最优阈值的误差均小于10%,为高精度的质心计算提供了一种较好的阈值处理方法.

图6 (a)处理前的SHWFS典型图像;(b)处理后的SHWFS图像;(c)各个孔径光斑图像的SNRFig.6.(a)The image in the SHWFS before processed;(b)the image in the SHWFS after processed using the presented method;(c)the SNR of all the apertures.

图7 (网刊彩色)实验条件下各种阈值估计方法与理论最优阈值的误差Fig.7.(color online)The error between the theoretic threshold and the threshold obtained by di ff erent methods.

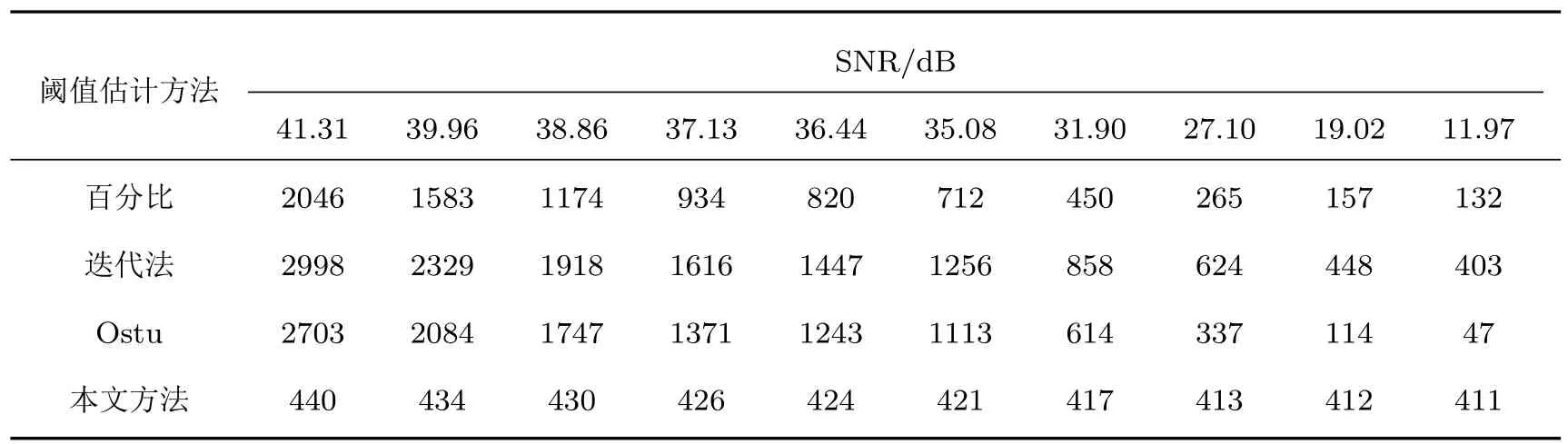
表1 不同SNR条件下各种方法对应的估计阈值比较(单位:ADU)Table 1.The estimated threshold using the di ff erent methods with the di ff erent SNR(unit:ADU).

5 结 论

本文针对SHWFS探测系统中,子孔径光斑呈现高斯分布、噪声随时间变化比较快且空间分布不均匀的特点,提出了一种利用滑动窗口均值、滑动窗口内像素局部梯度方,即像素与x-y平面夹角作为参数,构造噪声权重函数的最优阈值估计方法.比较了这种方法以及迭代阈值法、最大值百分比阈值法和Ostu法等典型的阈值处理方法结果与理论最优阈值的误差.仿真和实验结果表明,与典型的阈值处理方法相比,本文提出的方法能够得到更高精度最优阈值的估计值,并且在各种SNR条件下与理论最优阈值保持小于10%的误差.

[1]Li J,Gong Y,Hu X R,Li C C 2014Chin.J.Laser41 0316002(in Chinese)[李晶,巩岩,呼新荣,李春才2014中国激光41 0316002]

[2]Baik S H,Park S K,Kim C J,Cha B 2007Opt.Laser Technol.39 262

[3]Zhu Z Y,Li D Y,Hu L F,Mu Q Q,Yang C L,Cao Z L,Xuan L 2016Chin.Phys.B25 090702

[4]Gao C Q,Gao M W,Weber H 2004Chin.Phys.Lett.21 2191

[5]Wei L,Shi G H,Lu J,Yang J S,Li X Q,Zhang Y D 2013J.Opt.15 055702

[6]Chen L H,Rao C H 2011Acta Phys.Sin.60 090701(in Chinese)[陈林辉,饶长辉 2011物理学报 60 090701]

[7]Li C H,Xian H,Jiang W H,Rao C H 2007Acta Phys.Sin.56 4289(in Chinese)[李超宏,鲜浩,姜文汉,饶长辉2007物理学报56 4289]

[8]Ares J,Arines J 2001Opt.Lett.26 1831

[9]Ma X Y,Rao C H,Zheng H Q 2009Opt.Express17 8525

[10]Liang C,Liao W H,Shen J X,Zhou Y 2009Chin.J.Laser36 430(in Chinese)[梁春,廖文和,沈建新,周宇2009中国激光36 430]

[11]Ren J F,Rao C H,Li M Q 2002Opto-Electron.Eng.29 1(in Chinese)[任剑峰,饶长辉,李明全2002光电工程29 1]

[12]Thatiparthi C,Ommanib A,Burmanc R,Thapa D,Hutchings N,Lakshminarayanan V 2016Proc.SPIE9693 969321

[13]Thomas S 2004Proc.SPIE5490 1238

[14]Nightingale A M,Gordeyev S 2013Opt.Eng.52 071413

[15]Shen F,Jiang W H 1999High Power Laser and Particle Beams11 27(in Chinese)[沈锋,姜文汉 1999强激光与粒子束11 27]

[16]Li Y K,Zhang J Z,Zhang F Z 2014Proc.SPIE9242 92421V

PACS:07.07.Df,05.40.Ca,42.25.Bs,95.75.QrDOI:10.7498/aps.66.090701

Shack-Hartmann optimum threshold estimation for the point source

Zhou Rui1)2)3)†Wei Ling1)2)Li Xin-Yang1)2)Wang Cai-Xia1)2)Li Mei1)2)Shen Feng1)2)

1)(Key Laboratory on Adaptive Optics,Chinese Academy of Sciences,Chengdu 610209,China)2)(Institute of Optics and Electronics,Chinese Academy of Sciences,Chengdu 610209,China)3)(University of Chinese Academy of Sciences,Beijing 100049,China)

8 November 2016;revised manuscript

4 February 2017)

Shack-Hartmann wavefront sensor,Gaussian spot,optimum thresh,weighted function

10.7498/aps.66.090701

The Shack-Hartmann wavefront sensor(SHWFS)is an optical detection device based on the measurements of wavefront slopes.It is widely used in an adaptive optics system due to its simple structure and strong environment adaptability.The measuring accuracy of the SHWFS depends mainly on the accuracy of the spot image centroid in each sub-aperture.There are many centroid algorithms including the center of gravity algorithm,Gauss fi tting algorithm,and correlation algorithm.As to the simplicity,robustness,high accuracy and stability,the center of gravity algorithm is more widely used.However,the accuracy of gravity algorithm is sensitive to the noise including discretization,aliasing,photon noise,readout noise,stray light,and direct current bias.To improve the accuracy of centroid,the output signals of SHWFS must be pre-processed to suppress the noise e ff ect by using the method of thresholding in general.Many threshold methods have been presented to reduce the error of centroid and there theoretically exists an optimum threshold which causes the minimum error of centroid based on the characteristics of SHWFS and noise.However,it is difficult to separate the signals from the noises,and the optimum threshold cannot be estimated accurately in real time in the SHWFS systems.In this paper aiming at noises in SHWFS,which vary with time and space rapidly,a method based on the noise weighted function of the mean value of pixels and the local gradient direction of image signals in the moving windows is presented according to the characteristics of the Gaussian spot and noise distributions.Moreover,the theory and parameters determination of the method are analyzed.The method utilizes the probability that the pixels in the moving windows belong to the noise,and the probability is inversely proportional to the mean value of pixels and the local gradient direction of image signals,and so the monotonically reducing probability function of pixels is constructed.Finally,the standard deviation and mean value of noise can be obtained,and the estimation value of optimum threshold is equal to the mean value of noise plus three times the standard deviation of noise.To investigate the e ff ects of the optimum threshold estimation with the di ff erent spot sizes,spot strengths and noise levels,the proposed algorithm is compared with traditional methods.The simulation and experimental results show that the proposed method could achieve higher accuracy,and the error between the threshold obtained by the method presented in this paper and theoretical optimum threshold is less than 10%,which is less than those from the traditional methods.

†通信作者.E-mail:zhourui@ioe.ac.cn

†Corresponding author.E-mail:zhourui@ioe.ac.cn