不确定分数阶时滞混沌系统自适应神经网络同步控制∗

林飞飞 曾喆昭

(长沙理工大学电气与信息工程学院,长沙 410076)

不确定分数阶时滞混沌系统自适应神经网络同步控制∗

林飞飞 曾喆昭†

(长沙理工大学电气与信息工程学院,长沙 410076)

(2016年12月21日收到;2017年1月13日收到修改稿)

针对带有完全未知的非线性不确定项和外界扰动的异结构分数阶时滞混沌系统的同步问题,基于Lyapunov稳定性理论,设计了自适应径向基函数(radial basis function,RBF)神经网络控制器以及整数阶的参数自适应律.该控制器结合了RBF神经网络和自适应控制技术,RBF神经网络用来逼近未知非线性函数,自适应律用于调整控制器中相应的参数.构造平方Lyapunov函数进行稳定性分析,基于Barbalat引理证明了同步误差渐近趋于零.数值仿真结果表明了该控制器的有效性.

分数阶时滞混沌系统,Barbalat引理,自适应RBF神经网络控制

1 引 言

分数阶微积分起源于17世纪,但是由于缺乏有效的计算手段对其研究一直处于纯数学领域而发展缓慢.随着计算机技术的不断发展,分数阶微积分在工程实际和物理学中的应用已成为热点［1−4].在对分数阶微积分不断深入研究的过程中,人们普遍认为分数阶微积分是整数阶微积分的自然推广,整数阶微积分是分数阶微积分的一种特殊情况［5].关于复杂系统的建模问题,分数阶微积分模型比整数阶微积分模型更加准确,同时还能包含系统的遗传和记忆效应［6].因此,研究分数阶系统更加具有普遍意义.

随着研究分数阶微积分的热潮兴起,分数阶微积分被推广到混沌系统中.人们发现分数阶混沌系统具有整数阶混沌系统几乎所有的特点,并且由于其具有历史记忆特性,分数阶混沌系统往往比整数阶混沌系统具有更加复杂的动力学行为,在图像加密［7]、保密通信［8]和生物医学［9]等领域具有广阔的应用前景.混沌同步是非线性科学中的重要分支之一,其应用范围包括安全通信、生物网络和物理系统等领域,从而引起了人们的广泛研究,并提出了大量的同步控制方法.主要有自适应脉冲同步［10]、修正投影同步［11]、滑模控制同步［12]、自适应同步［13]、自适应模糊控制同步［14]、自适应滑模控制同步［15]等,以上方法都是关于分数阶混沌系统的同步控制,是否适用于分数阶时滞混沌系统还有待研究.

时滞是自然界中普遍存在的现象［16],由于摩擦、机械等实际因素的影响,实际系统总是存在时滞现象,如物理、机械、经济、生物和工程学等,另外时滞对系统的动态特性有重要影响.当系统的变化不仅依赖于当前的状态,还依赖于过去的状态时,则该系统称为时滞系统.从理论上讲,时滞的存在使得系统更为复杂,所以研究时滞混沌系统的同步控制是一项更具挑战意义的课题［17];从实际角度而言,由于分数阶时滞混沌系统更接近现实生活且动力学行为更加复杂,因此,研究分数阶时滞混沌系统的动力学行为及其同步控制具有重要的实际意义.人们分别对分数阶时滞Duffing混沌系统［18]、分数阶时滞金融混沌系统［19]、分数阶时滞Liu混沌系统［20]、分数阶时滞Chen混沌系统［21]进行了数值仿真实验,研究了不同时滞量的情况下系统的动力学行为,以上研究为分数阶时滞混沌系统的同步控制提供了一定的理论基础.其中,文献[22]针对分数阶时滞金融混沌系统在含不确定项的情况下的同步控制问题,设计了一种滑模控制器,该控制器实现了分数阶时滞金融混沌系统的自同步控制,但该控制器要求不确定项有界且没有考虑外界扰动,另外该控制器无法实现异结构分数阶时滞混沌系统的同步控制.文献[23,24]采用主动控制的思想对非线性项进行了直接消除,使得系统的系数矩阵成为定常矩阵,实现了分数阶时滞混沌系统的混合投影同步,但其控制代价较大,而且当系统存在未知不确定项时,该方法无法达到预期的控制效果.文献[25]实现了分数阶时滞混沌系统脉冲同步,但该控制器需要知道驱动系统和响应系统线性部分的系数矩阵,对系统模型具有很强的依赖性,当系统存在不确定项或外界扰动时,该方法难以实现同步控制.另外,以上所有的控制方法都只适用于驱动系统和响应系统时滞量相同情况下的同步控制.

在实际的物理系统中,混沌系统一般是不确定的或未知的,还可能受到外界扰动的影响,另外系统在运行过程中存在元器件老化和衰退的情况,以上因素使得理想模型无法精确地描述实际系统.一方面,径向基函数(RBF)神经网络作为一种局部逼近网络已经被证明能以任意精度逼近任意连续函数［26,27],所以可以用RBF神经网络来估计未知系统模型.另一方面,自适应控制能够通过自动调节控制器的相关参数消除不确定性和复杂因素的影响,从而使控制器与被控对象和环境相适应.基于以上考虑,本文主要研究了基于自适应RBF神经网络的不确定分数阶时滞混沌系统的同步控制问题.RBF神经网络用来估计未知非线性函数,自适应律用于调整控制器中的相应参数,在所设计的同步控制器的作用下,同步误差渐近趋于零.本文的主要工作如下:1)基于Barbalat引理和Lyapunov稳定性理论,设计了一种自适应RBF神经网络控制器以及参数自适应律,该控制器是在完全未知混沌系统非线性函数模型、非线性不确定项和外界扰动的情况下实现了分数阶时滞混沌系统同步控制;2)在稳定性分析中构造了相应的平方Lyapunov函数,并直接对其进行整数阶求导,结合Barbalat引理和引理6证明了同步误差渐近趋于零,运用该方法避免了对平方Lyapunov函数进行分数阶求导,同时保证了自适应律为整数阶;3)数值仿真实现了以不确定分数阶时滞Liu混沌系统为驱动系统,不确定分数阶时滞Chen混沌系统为响应系统,在含随机扰动情况下的同步控制,理论证明和仿真结果表明了该控制器的有效性.

2 预备知识

2.1分数阶微积分概述

分数阶微积分在其发展过程中产生了多种定义,其中常用的有Riemann-Liouville(R-L)定义、Caputo定义.本文选取Caputo定义进行研究.

Caputo分数阶积分定义为

Caputo分数阶微分定义为

其中n为大于α的最小整数,n−1＜ α＜n;Γ(.)为伽马函数,分数阶微分(2)式的Laplace变换定义为［24]

下面给出一些将要用到的性质和结论.

性质1［28]分数阶微积分的线性性质

其中,α∈R,a和b为常数.

引理1［29]若x(t)∈C1[0,T](T＞0),则下面等式成立:

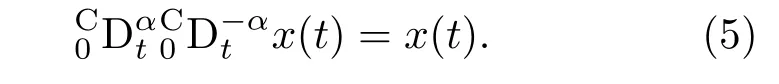
引理2［29]若x(t)∈C1[0,T](T＞ 0),其中α,β∈R+,且α+β=1则下面等式成立:

2.2 RBF神经网络描述

RBF神经网络是一种两层局部收敛的神经网络,因而具有很快的收敛速度.理论上已经证明它能以任意精度逼近任意连续函数.第一层为非线性输入层,即高斯基函数,其输出为

第二层为线性输出层,即

其中,X=[X1,X2,...,Xn]T为RBF神经网络的输入向量;n×m个中心值构成矩阵C=[c1,c2,...,cj,...,cm];cj=[c1j,c2j,...,cij,...,cnj]T和bj分别为RBF神经网络隐含层第j个结点的中心向量和宽度;Wi=[wi1,wi2,...,wim]T为网络的权值向量;H=[h1,h2,...,hm]T为高斯基函数向量.

3 同步控制器设计及稳定性分析

3.1同步控制问题描述

考虑n维分数阶时滞混沌系统,设驱动系统和响应系统分别为

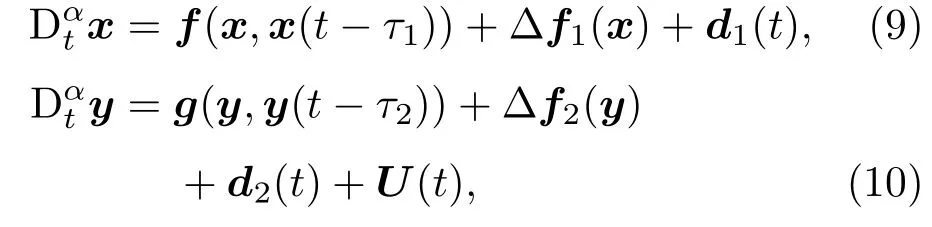
式中x=[x1(t),x2(t),...,xn(t)]T∈ Rn,y=[y1(t),y2(t),...,yn(t)]T∈ Rn分别为驱动系统和响应系统可测的状态变量;

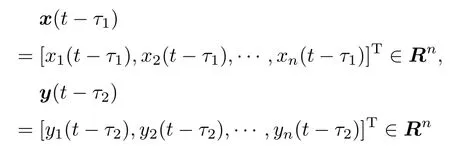
为含时滞状态变量; Δf1(x)=[Δf11,Δf12,...,Δf1n]T∈ Rn,Δf2(y)=[Δf21,Δf22,...,Δf2n]T∈Rn为非线性不确定项;d1(t)=[d11(t),d12(t),...,d1n(t)]T和d2(t)=[d21(t),d22(t),...,d2n(t)]T为外界扰动项,其中Δf1(x),Δf2(y),d1(t),d2(t)是完全未知的;f,g:Rn→Rn为未知的非线性函数;U(t)=[u1(t),u2(t),...un(t)]T为待设计控制器.

定义响应系统(10)和驱动系统(9)的同步误差为e(t)=y(t)−x(t);误差向量为e(t)=[e1(t),e2(t),...,en(t)]T. 当时,即同步误差渐近趋于零时,驱动系统(9)和响应系统(10)实现同步.

3.2基于RBF神经网络控制器设计

由响应系统(10)式减去驱动系统(9)式得到同步误差系统为

其中H高斯基函数向量,Wi为RBF神经网络权值向量.令RBF神经网络最优估计参数为W∗i,则最优估计为

设RBF神经网络的参数误差和最优估计误差分别为

其中,RBF神经网络的估计误差是有界的［27],即为最优估计误差的上界. 未知非线性函数的估计误差为

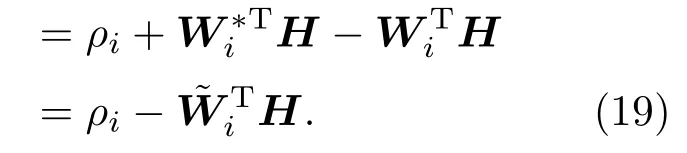
根据上面的讨论,同步控制器可设计为

式中,ki是最优逼近误差上界的估计值,li为反馈增益为常数)的估计值.RBF神经网络权值、最优逼近误差上界的估计值ki和反馈增益的估计值li的整数阶自适应律分别为

式中λi＞0,γi＞0,ξi＞0(i=1,2,...,n)为自适应律的调节参数.

3.3系统稳定性分析

本节首先给出稳定性证明过程中所需的相关引理,然后分析控制器作用下同步误差系统的稳定性.

引理3若x(t)∈C1[0,T](T＞0),则下面等式成立:

证明设由引理1可得

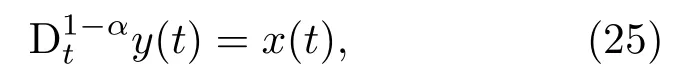
根据引理2可知

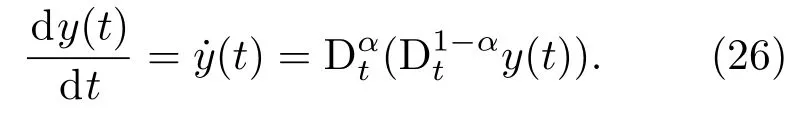
将(25)式代入(26)式有

所以

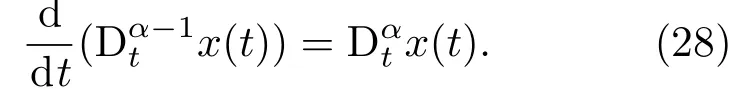
引理4设x(t)∈ R,则且

证明由(1)式可以得到

由Gamma函数的定义易知,Γ(1−α)＞ 0.又τ∈ [0,t−],因此,(t− τ)−α|x(τ)|≥ 0.

引理5［30](Barbalat引理)设

即x(t)∈L2;同时当x(t)∈L∞,如果(t),t∈[0,∞)存在且有界,即(t)∈L∞,那么

引理6如果渐近稳定,即

证明由引理1可知

对(32)式进行Laplace变换,

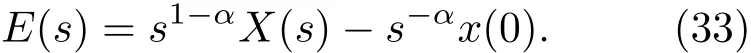
根据终值定理有

定理1给定初始条件,在设计的自适应RBF神经网络控制器(20)和自适应律(21),(22)和(23)的作用下可实现驱动系统(9)和响应系统(10)的同步控制,同步误差渐近趋于零.

证明将同步控制器(20)代入(14)式可得

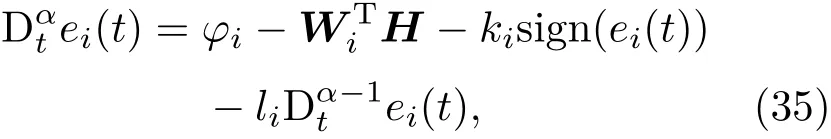
由(15)和(19)式进一步有

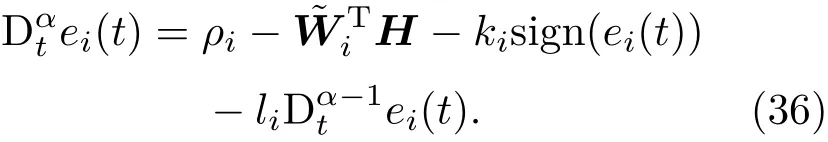
构造Lyapunov函数

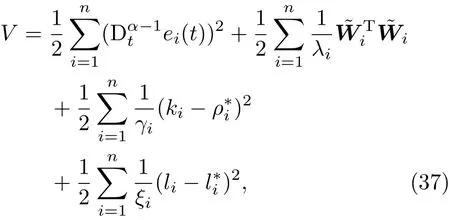
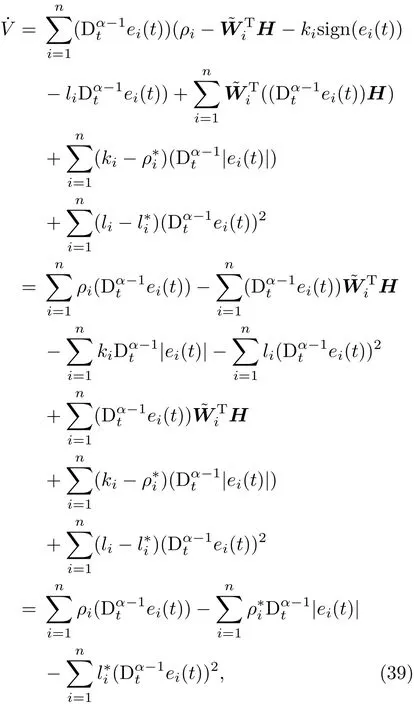
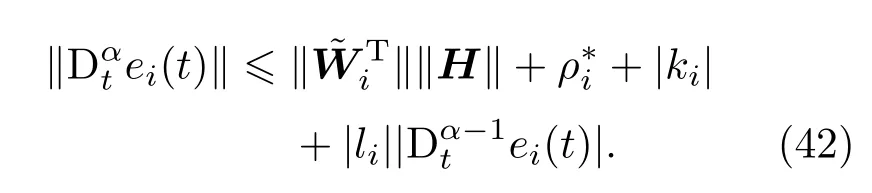
所以,同步误差渐近趋于零.定理1证毕.

4 数值仿真

为了验证本文所设计的控制器的有效性,应用改进型预估-校正方法［31]对不确定分数阶Liu时滞混沌系统和不确定分数阶Chen时滞混沌系统进行同步控制数值仿真.本文的控制器是在混沌系统非线性函数模型、非线性不确定项和外界扰动完全未知的情况下的同步控制,以下给出了仿真需要的相关模型.

分数阶时滞Liu混沌系统［20]为

根据文献[20]可知α=0.97,0＜τ1≤0.005时,系统处于混沌状态.所以,选取α=0.97,τ1=0.005.状态初值为x(0)=[2.2,2.4,3.8]T.当t∈[−τ1,0)时,x1(t)=2.2,x2(t)=2.4,x3(t)=3.8.系统表现为混沌状态,如图1所示.

分数阶Chen时滞混沌系统［21]为

根据文献[21]可知α=0.97,τ2=0.009时,系统处于混沌状态.所以,选取α=0.97,τ2=0.009.状态初值为y(0)=[0.2,0,0.5]T. 当t∈ [−τ2,0)时,y1(t)=0.2,y2(t)=0,y3(t)=0.5.系统表现为混沌状态,如图2所示.

分数阶时滞Liu混沌系统加入非线性不确定项和随机扰动后,作为驱动系统,

图1 τ1=0.005时分数阶时滞Liu混沌系统Fig.1.Fractional-order Liu system with time delay for τ1=0.005.

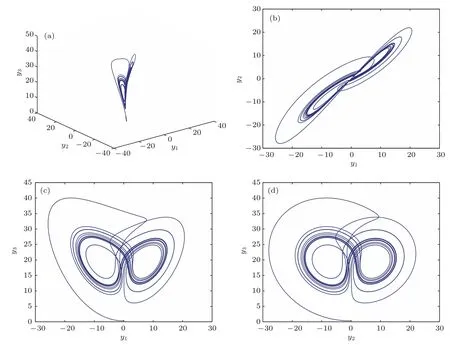
图2 τ2=0.009时分数阶时滞Chen混沌系统Fig.2.Fractional-order Chen system with time delay for τ2=0.009.

分数阶时滞Chen混沌系统加入非线性不确定项和随机扰动后,作为响应系统,其中,参数自适应律为

RBF神经网络系统的输入变量为可测状态变量x和y.在数值仿真中用同步误差变量e代替x和y,以减少RBF神经网络系统的运算量.隐层神经元个数为9,中心值矩阵为

图3 (网刊彩色)同步控制结果 (a)同步误差e1,e2,e3;(b)状态变量x1,y1;(c)状态变量x2,y2;(d)状态变量x3,y3Fig.3.(color online)Synchronization control results:(a)The synchronization errors of e1,e2,e3;(b)the state variables of x1,y1;(c)the state variables of x2,y2;(d)the state variables of x3,y3.

图4 (网刊彩色)神经网络权值‖W1‖,‖W2‖,‖W3‖Fig.4.(color online)Neural network weights ‖W1‖,‖W2‖,‖W3‖.

宽度值bj=3(j=1,2,...,9).自适应律的调节参数λi=3×104,γi=3.5,ξi=5(i=1,2,3);RBF神经网络权值的初值W1(0),W2(0)和W3(0)均为9维的零向量.自适应律初值k1(0)=0.01,k2(0)=0.01,k3(0)=0.01;l1(0)=5,l2(0)=5,l3(0)=5;时间步长h=0.001,进行数值仿真,仿真结果如图3和图4所示.由图3(a)可以看出同步误差收敛较快,说明设计的RBF神经网络具有良好的逼近效果;从图3(b)—(d)可以看到各状态同步效果较好.由图4可以看出RBF神经网络权值振幅不大,变化较平稳.从以上仿真结果可知本文所设计的同步控制器的控制效果较好.

5 结 论

本文针对异结构分数阶时滞混沌系统,在含非线性不确定项和随机扰动情况下的同步问题,基于Lyapunov稳定性理论设计了一种自适应RBF神经网络控制器.在稳定性分析中直接对相应的平方Lyapunov函数进行整数阶求导,避免对其进行分数阶求导,结合相关引理证明了误差系统渐近趋于零.与目前关于分数阶时滞混沌系统的同步控制方法［22−25]相比,本文所设计的控制器不依赖于系统模型且能够实现在非线性不确定项和外界扰动完全未知情况下的同步控制.仿真结果表明该控制器不仅实现了异结构分数阶时滞混沌系统的同步控制,而且响应速度较快、控制效果良好、抗干扰能力较强.从长远的应用角度来看,异结构同步比自同步具有更大的研究价值和发展前景.因此,本文的研究结果既具有重要的理论意义,同时在保密通信领域也具有较大的应用价值.

[1]Hermann R 2010Physica A389 4613

[2]Li C L,Yu S M,Luo X S 2012Chin.Phys.B21 100506

[3]Peterson M R,Nayak C 2014Phys.Rev.Lett.113 086401

[4]Maione G 2013IEEE Trans.Autom.Control58 1579

[5]Hu J B,Zhao L D 2013Acta Phys.Sin.62 240504(in Chinese)[胡建兵,赵灵冬 2013物理学报 62 240504]

[6]Chen D Y,Zhang R F,Liu X Z,Ma X Y 2014Commun.Nonlinear Sci.Numer.Simulat.19 4105

[7]Balasubramaniam P,Muthukumar P,Ratnavelu K 2015Nonlinear Dyn.80 249

[8]Muthukumar P,Balasubramaniam P,Ratnavelu K 2015Nonlinear Dyn.80 1883

[9]Gao F,Li T,Tong H Q,Ou Z L 2016Acta Phys.Sin.65 230502(in Chinese)[高飞,李腾,童恒庆,欧卓玲2016物理学报65 230502]

[10]Andrew L Y T,Li X F,Chu Y D,Zhang H 2015Chin.Phys.B24 010502

[11]Gao Y,Liang C H,Wu Q Q,Yuan H Y 2015Chaos Soliton.Fract.76 190

[12]Khanzadeh A,Pourgholi M 2016Chaos Soliton.Fract.91 69

[13]Maheri M,Ari fi n N M 2016Nonlinear Dyn.85 825

[14]Chen Y,Li S G,Liu H 2016Acta Phys.Sin.65 170501(in Chinese)[陈晔,李生刚,刘恒 2016物理学报 65 170501]

[15]Pan G,Wei J 2015Acta Phys.Sin.64 040505(in Chinese)[潘光,魏静 2015物理学报 64 040505]

[16]Wen S F,Shen Y J,Yang S P 2016Acta Phys.Sin.65 094502(in Chinese)[温少芳,申永军,杨绍普2016物理学报65 094502]

[17]Zhang H G,Ma T D,Huang G B,Wang Z L 2010IEEE Trans.Syst.Man Cybern.B:Cybern.40 831

[18]Deng W H,Li C P,Lü J H 2007Nonlinear Dyn.48 409

[19]Wang Z,Huang X,Shi G D 2011Comput.Math.Appl.62 1531

[20]Bhalekar S,Daftardar-Gejji V 2010Commun.Nonlinear Sci.Numer.Simulat.15 2178

[21]Daftardar-Gejji V,Bhalekar S,Gade P 2012Pramana79 61

[22]Liu H R,Yang J 2015Entropy17 4202

[23]Wang S,Yu Y G,Wen G G 2014Nonlinear Anal.Hybrid Syst.11 129

[24]Velmurugan G,Rakkiyappan R 2016ASME J.Comput.Nonlinear Dyn.11 031016

[25]Li D,Zhang X P 2016Neurocomputing216 39

[26]Zeng Z Z 2013Acta Phys.Sin.62 030504(in Chinese)[曾喆昭 2013物理学报62 030504]

[27]Yan X M,Liu D,Guo H J 2010Control Theory Appl.27 344(in Chinese)[阎晓妹,刘丁,郭会军2010控制理论与应用27 344]

[28]Deng L W 2014Ph.D.Dissertation(Harbin:Harbin Institute of Technology)(in Chinese)[邓立为 2014博士学位论文(哈尔滨:哈尔滨工业大学)]

[29]Li C P,Deng W H 2007Appl.Math.Comput.187 777

[30]Tao G 1997IEEE Trans.Automat.Control42 698

[31]Bhalekar S,Daftardar-Gejji V 2011J.Fract.Calc.Appl.1 1

PACS:05.45.Pq,05.45.XtDOI:10.7498/aps.66.090504

Synchronization of uncertain fractional-order chaotic systems with time delay based on adaptive neural network control∗

Lin Fei-FeiZeng Zhe-Zhao†

(College of Electrical and Information Engineering,Changsha University of Science and Technology,Changsha 410076,China)

21 December 2016;revised manuscript

13 January 2017)

Time delay frequently appears in many phenomena of real life and the presence of time delay in a chaotic system leads to its complexity.It is of great practical signi fi cance to study the synchronization control of fractional-order chaotic systems with time delay.This is because it is closer to the real life and its dynamical behavior is more complex.However,the chaotic system is usually uncertain or unknown,and may also be a ff ected by external disturbances,which cannot make the ideal model accurately describe the actual system.Moreover,in most of existing researches,they are difficult to realize the synchronization control of fractional-order time delay chaotic systems with unknown terms.

In this paper,for the synchronization problems of the di ff erent structural fractional-order time delay chaotic systems with completely unknown nonlinear uncertain terms and external disturbances,based on Lyapunov stability theory,an adaptive radial basis function(RBF)neural network controller,which is accompanied by integer-order adaptive laws of parameters,is established.The controller combines RBF neural network and adaptive control technology,the RBF neural network is employed to approximate the unknown nonlinear functions,and the adaptive laws are used to adjust corresponding parameters of the controller.The system stability is analyzed by constructing a quadratic Lyapunov function.This method not only avoids the fractional derivative of the quadratic Lyapunov function,but also ensures that the adaptive laws are integer-order.Based on Barbalat lemma,it is proved that the synchronization error tends to zero asymptotically.In the numerical simulation,the uncertain fractional-order Liu chaotic system with time delay is chosen as the driving system,and the uncertain fractional-order Chen chaotic system with time delay is used as the response system.The simulation results show that the controller can realize the synchronization control of the di ff erent structural fractional-order chaotic systems with time delay,and has the advantages of fast response speed,good control e ff ect,and strong anti-interference ability.From the perspective of long-term application,the synchronization of di ff erent structures has greater research signi fi cance and more development prospect than self synchronization.Therefore,the results of this study have great theoretical signi fi cance,and have a great application value in the fi eld of secure communication.

fractional-order chaotic systems with time delay,Barbalat lemma,adaptive radial basis function neural network control

10.7498/aps.66.090504

∗国家自然科学基金(批准号:61040049)、电子科学与技术湖南省重点学科和智能电网运行与控制湖南省重点实验室项目资助的课题.

†通信作者.E-mail:508984293@qq.com

*Project supported by the National Natural Science Foundation of China(Grant No.61040049),the Hunan Province Key Discipline of Electronic Science and Technology,and the Foundation of Hunan Province Key Laboratory of Smart Grids Operation and Control,China.

†Corresponding author.E-mail:508984293@qq.com