四端双量子点系统中的自旋和电荷能斯特效应∗
2017-08-09郑军李春雷杨曦郭永4
郑军 李春雷 杨曦 郭永4)
1)(渤海大学新能源学院,锦州 121013)2)(首都师范大学初等教育学院,北京 100048)3)(清华大学物理系,北京 100084)4)(量子物质科学协同创新中心,北京 100084)
四端双量子点系统中的自旋和电荷能斯特效应∗
郑军1)†李春雷2)杨曦3)郭永3)4)
1)(渤海大学新能源学院,锦州 121013)2)(首都师范大学初等教育学院,北京 100048)3)(清华大学物理系,北京 100084)4)(量子物质科学协同创新中心,北京 100084)
(2016年12月20日收到;2017年1月20日收到修改稿)
基于非平衡态格林函数方法,理论研究了与四个电极耦合的双量子点系统中的自旋和电荷能斯特效应,考虑了不同电极的磁动量结构和量子点内以及量子点间电子的库仑相互作用对热电效应的影响.结果表明铁磁端口中的磁化方向能够有效地调节能斯特效应:当电极1和电极3中的磁化方向反平行排列时,通过施加横向的温度梯度,系统中将会出现纯的自旋能斯特效应;当电极4从普通金属端口转变为铁磁金属端口时,将同时观测到电荷和自旋能斯特效应.研究发现,能斯特效应对于铁磁电极极化强度的依赖程度较弱,但对库仑排斥作用十分敏感.在量子点内和点间库仑排斥作用的影响下,自旋及电荷能斯特系数有望提高两个数量级.
量子点,能斯特效应,库仑相互作用
1 引 言
随着电子元件集成度的提高,功耗及其相关的散热问题对器件性能的影响愈发明显.如何控制和再利用微型结构中的热能,对包括自旋电子学在内的电子科技有着重要意义[1].随着过去二十年间微细加工技术和低温测量技术的发展,低维结构中的热电测量变得更加灵活有效,器件的热输运过程也得到了越来越多的关注[2,3].近期,科研人员在高温超导体[4]、铁磁金属[5]、半金属[6]、单势垒碳纳米管[7]及量子点[8]等材料或结构中观测到了能斯特(Nernst)效应和赛贝克(Seebeck)效应.
电子具有电荷和自旋两个自由度.在思考半导体工业发展方向和新出路时,科研人员发现几乎所有的电子产品都只利用了电子作为电荷载体的属性来传输能量和信息,作为电子内禀性质的自旋,除了材料磁性和简单的能级简并外,几乎被完全忽略.这使研究人员在探索未来半导体工业发展时有了新的契机和可能的研究方向[9].基于电子自旋传输与调控的元件在工作时不严格依赖于静电势垒的升降,因而在一定程度上可以避免传统器件会遇到的尺寸效应,以实现更大规模的集成.此外,利用自旋电流在半导体材料中进行自旋传输,还可能降低传统器件带来的信息耗散.在固态材料中产生和控制自旋流,已经成为自旋电子学的主要研究课题[10,11].到目前为止,对纳米结构中电子自旋的电学、磁学和光学的调制技术已经日益成熟.
近期基于四端铁磁材料系统的实验中发现了一种新的热电现象,被称为自旋能斯特效应(spin Nernst e ff ect)[12]或横向自旋塞贝克效应(spin transverse Seebeck e ff ect).具体地,在水平方向的两个端口施加温度梯度,能够在垂直于温度梯度的端口观测到自旋压或自旋流.与两端系统相比,多端系统能够在其他温度相同的端口生成自旋压或自旋流.此外,就纳米电路而言,多端连接是必要的.自旋能斯特效应引入了一种通过调节热偏压产生和控制电流的方法,由于其潜在的应用价值,逐渐成为理论和实验研究的热点,科研人员在多种材料中研究了这一效应.例如,Checkelsky和Ong[13]通过实验研究了磁场下石墨烯中的能斯特效应,发现能斯特系数在磁场条件下随着门电压的变化出现强烈的量子振荡,这一现象在狄拉克点附近将得到极大的增强.Cyr-Choiniere等[14]在高温超导体中开展了针对能斯特效应的理论研究,并发现金属材料中的能斯特效应对超导相变和密度波相变高度敏感.Tauber等[15]理论计算了理想晶体中杂质对电子自旋散射引起的能斯特效应的影响,发现自旋电流的流向依赖于杂质,可以通过改变杂质的类型来调制自旋电流的极化方向和大小.Cheng等[16]理论研究了存在自旋轨道耦合的二维交叉(cross bar)结构中的电荷和自旋能斯特效应,研究发现自旋轨道耦合能够导致能斯特峰发生劈裂,自旋能斯特系数随着自旋轨道耦合强度的增大而增加,但是随着磁场的增强而减弱.目前关于自旋能斯特效应在量子点系统中的研究仍然比较有限.基于格林函数方法,近期我们理论研究了量子点环系统中的自旋和电荷能斯特效应.研究发现在Rashba自旋轨道耦合辅助下,无需外加磁场即可在系统中产生纯的自旋能斯特效应,并且自旋电流的大小和方向可以通过自旋轨道耦合相位和磁通调控.
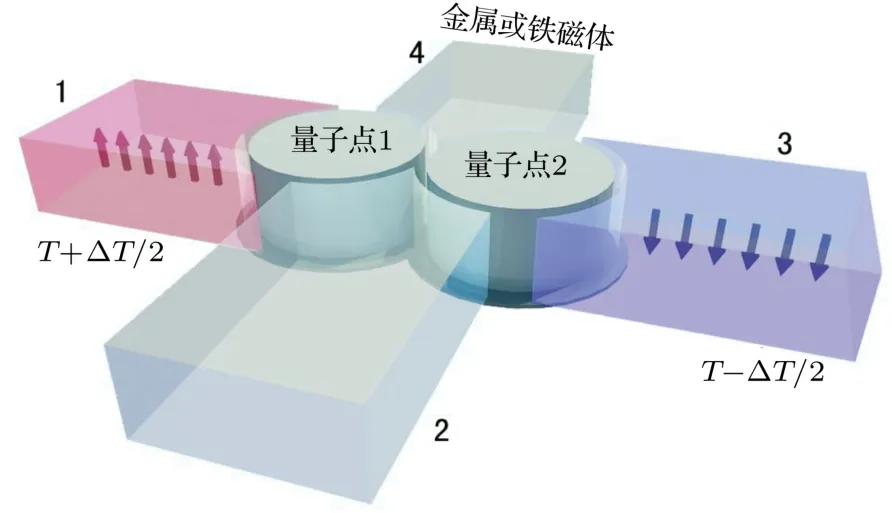
图1 (网刊彩色)平行排列双量子点耦合四个端口的系统示意图,其中,左、右两铁磁端口中的温度分别为T1=T+ΔT/2和T3=T−ΔT/2,系统的平衡态温度为T=0.01ΓFig.1. (color online)Schematic plot of two parallel quantum dots coupled to four leads.The temperatures of the left and the right ferromagnetic leads are individually T1=T+ΔT/2,T3=T−ΔT/2.The system equilibrium temperature is fi xed at T=0.01Γ.
本文主要研究四端双量子点系统的热电输运特性.如图1所示,双量子点通过势垒与四个端电极耦合,电极1和电极3的温度分别维持在T+ΔT/2及T−ΔT/2,其中ΔT是两个铁磁电极间的横向温度梯度.讨论了电极1和电极3的磁化方向位形、电极4的属性以及量子点内和点间电子的库仑相互作用对自旋(电荷)能斯特效应的影响.
2 研究方法
四电极双量子点系统的哈密顿量可表示为[17,18]

利用Landauer-Büttiker公式,电极j中的平均电流可写成[19,20]


其中线宽函数矩阵元Γ1(1,1)=2π|t11|2ρj(ω),Γ3(2,2)=2π|t22|2ρj(ω),Γ2(i,i)=2π|t2i|2ρj(ω),Γ4(i,i)=2π|t4i|2ρj(ω). 无耦合的推迟(超前)格林函数为对角化矩阵,其矩阵元为

其中{n-i}≡ n-i−[n-i],[ni]是 ni= ni↑+ni↓的整数部分;niσ是量子点内自旋为σ电子的占据数. 这一占据数能够利用公式niσ=自洽求解,其中

(6)式中fj(ω)={1+exp[(ω−µi)/kBTi]}−1是化学势为µi、温度为Ti时电极j中电子的费米-狄拉克分布函数;其中T1=T+0.5ΔT,T3=T−0.5ΔT,T2=T4=T.在线性响应区域对ΔT和ΔV进行一阶泰勒展开,自旋相关的能斯特系数Nσ=J2σ/ΔT可以写成:

其中f0=[e(E−EF)/kBT+1]−1是零偏压和零温度梯度下的费米分布函数.自旋能斯特系数Ns和电荷能斯特系数Nc可以定义为:Ns=[N↑−N↓]和Nc=[N↑+N↓].
3 结果与讨论
在计算中,我们假设量子点与电极之间的耦合强度满足tji=0.4,且令作为能量单位. 我们固定系统的平衡温度T=0.001Γ,并仅考虑1,2两个量子点能级相同(ε1=ε2=εd)的情况.
3.1电极磁化方向对能斯特效应的调制
图2给出了铁磁电极1和电极3的磁化方向及强度对能斯特效应的影响.首先,我们讨论两个镍电极(P=0.3)磁化方向平行排列(ρ1σ=ρ3σ)的情况.如图2(a)所示,不同路径中不同自旋取向电子的透射概率相同T21σ=T23σ,且在εd=0位置出现峰值.这种现象可以通过电极1(3)到电极2的等效耦合强度[21]来解释:电子从电极1隧穿进入电极2的过程,包含三条干涉路径:1)电极1→量子点1→电极2;2)电极1→量子点1→电极4→量子点2→电极2;3)电极1→量子点1→电极4→电极3→电极2.在仅考虑一阶隧穿过程时,等效耦合强度T21为

类似地,我们可以得到电子从端口2到端口3之间的等效耦合强度T23σ:

当电极1与电极3中磁矩的磁化方向呈现反平行排列时,即ρ1↑=ρ3↓=(1+P),ρ1↓=ρ3↑=(1−P).如图2(a)所示,当且仅当P ̸=0时,自旋向上和自旋向下的透射概率互不相等且满足T21↑ =T23↓,T21↓ =T23↑.此时T21↑−T23↑ =因此可以从(7)式得到Ns=N↑−N↓0,但是Nc=N↑+N↓=0.这表明,在横向温度梯度作用下,该系统中能够观测热电效应激发的纯自旋流.随着P从0增大到1,自旋向上和自旋向下的能斯特系数之间的差距将会变大,因此自旋能斯特效应将有所增强(图2(c)).对于半金属铁磁材料作为电极的系统(P1)中,此时自旋能斯特系数能够达到Ns=0.002Γ/eT.

图2 (网刊彩色)P1=P3=P=0.3时,电极1和电极3磁化方向平行(P)和反平行(AP)排列情况下,(a)透射概率Tσ和(b)自旋相关的能斯特系数Nσ随着量子点内能级εd的变化;(c)自旋(电荷)能斯特系数Ns(c)在电极1和电极3磁化方向反平行排列且P取不同值时随量子点内能级εd的变化Fig.2. (color online)(a)The transmission coefficient Tσand(b)the spin dependent Nernst coefficient Nσas a function of the dots’level εdfor parallel(P)and antiparallel(AP)con fi guration with P1=P3=P=0.3;(c)the spin(charge)Nernst coefficient Ns(c)versus the dots’level εdfor antiparallel con fi guration with di ff erent values of P.
3.2电极4的属性对能斯特效应的影响
在图3中,我们研究了电极4的属性对能斯特效应的影响.当电极4从普通金属(图2中对应的情况)转变为铁磁金属时,电极3(1)与电极2之间的等效耦合强度T21(3)σ可以改写为:T21(3)σ=由此可得T21↑< T23↓,T21↓< T23↑(图3(a)). 由(7)式我们可以得出N↑̸=N↓,并且图3(b)中自旋依赖的能斯特系数Nσ在电子-空穴平衡点εd=0附近呈现出不对称的形状.这是由于当铁磁电极中的磁化方向反平行排列时,左电极中自旋向上和自旋向下电子的费米能满足εk1↑>εk1↓,而右电极中不同自旋方向电子的费米能满足εk2↑< εk1↓.温度相对较高的电极中有更多的自旋为σ的电子被激发到费米能εk1σ之上,费米能εk1σ之下的空穴数量相应地增加.电子和空穴对能斯特效应的贡献是互相抵消的,当量子点内的能级εd<0时,自旋向上的空穴(或自旋向下的电子)将成为主要载流子,此时的能斯特系数为正(负).当能级εd>0时,自旋向上(或自旋向下)的载流子主要是电子(或空穴),此时N↑(N↓)为负(正).对εd=0的情况,量子点内能级二重简并,此时电子和空穴对能斯特系数Nσ的贡献大小相同、符号相反,因此有Nσ=0.当εd̸=0时,自旋能斯特系数Ns=N↑−N↓以及电荷能斯特系数Nc=N↑+N↓同时存在有限值,如图3(c)所示,此时由于电极4的辅助作用,在系统中将同时观测到电荷和自旋能斯特效应.

图3 (网刊彩色)P1=P3=P4=P=0.3时,电极1和电极3磁化方向反平行排列情况下,(a)透射概率Tσ、(b)自旋相关的能斯特系数Nσ和(c)自旋(电荷)能斯特系数Ns(c)随着量子点内能级εd的变化Fig.3.(color online)(a)The transmission coefficient Tσ,(b)the spin dependent Nernst coefficient Nσ,and(c)the spin(charge)Nernst coefficient Ns(c)as a function of the dots’level εdfor antiparallel con fi guration with P1=P3=P4=P=0.3.
3.3库仑相互作用对能斯特效应的影响
图4中,我们讨论了量子点间与量子点内的库仑相互作用对热电输运的影响.首先,在图4(a)中仅考虑了点内库仑排斥作用的影响.对于多电极双量子点系统很难定义共振通道和相干通道,但是在分子能级表象下,双量子点系统可以改写为双分子态.透射系数在分子态εd=0和εd=−Uin时将出现两个峰值.当量子点能级εd=−Uin/2时,电子能够从左端高温电极经过高分子态流向右电极,空穴则从左端口经过低分子态流向右电极,因此εd=−Uin/2附近,透射概率值较小.根据自旋相关的能斯特系数的定义可知,为了抵消作用于载流子的热驱动以达到电流为零的条件,需要对电导值小的情况施加较大的偏压,这就导致了更为显著的能斯特效应.因此如图4(a)所示的数值计算结果表明,自旋相关的能斯特系数Nσ在分子态的区域非常小,只有在中间区域能够观测到很大的Nσ值.
图4(b)中给出了量子点间电子的库仑排斥势Uex对能斯特效应的影响.当量子点内电子的库仑相互作用与量子点间电子的库仑相互作用同时出现时,此时系统共出现四个分子态,因此在图4(b)中自旋相关的能斯特系数Nσ呈现三个峰.与图4(a)中讨论过的原因类似,能斯特效应将会通过点间库仑排斥作用得到进一步加强.如图4(c)所示,在量子点间电子库仑相互作用和点内库仑相互作用的共同影响下,能斯特系数能达到0.6Γ/eT,相比不存在库仑排斥作用的情况提高了两个数量级.
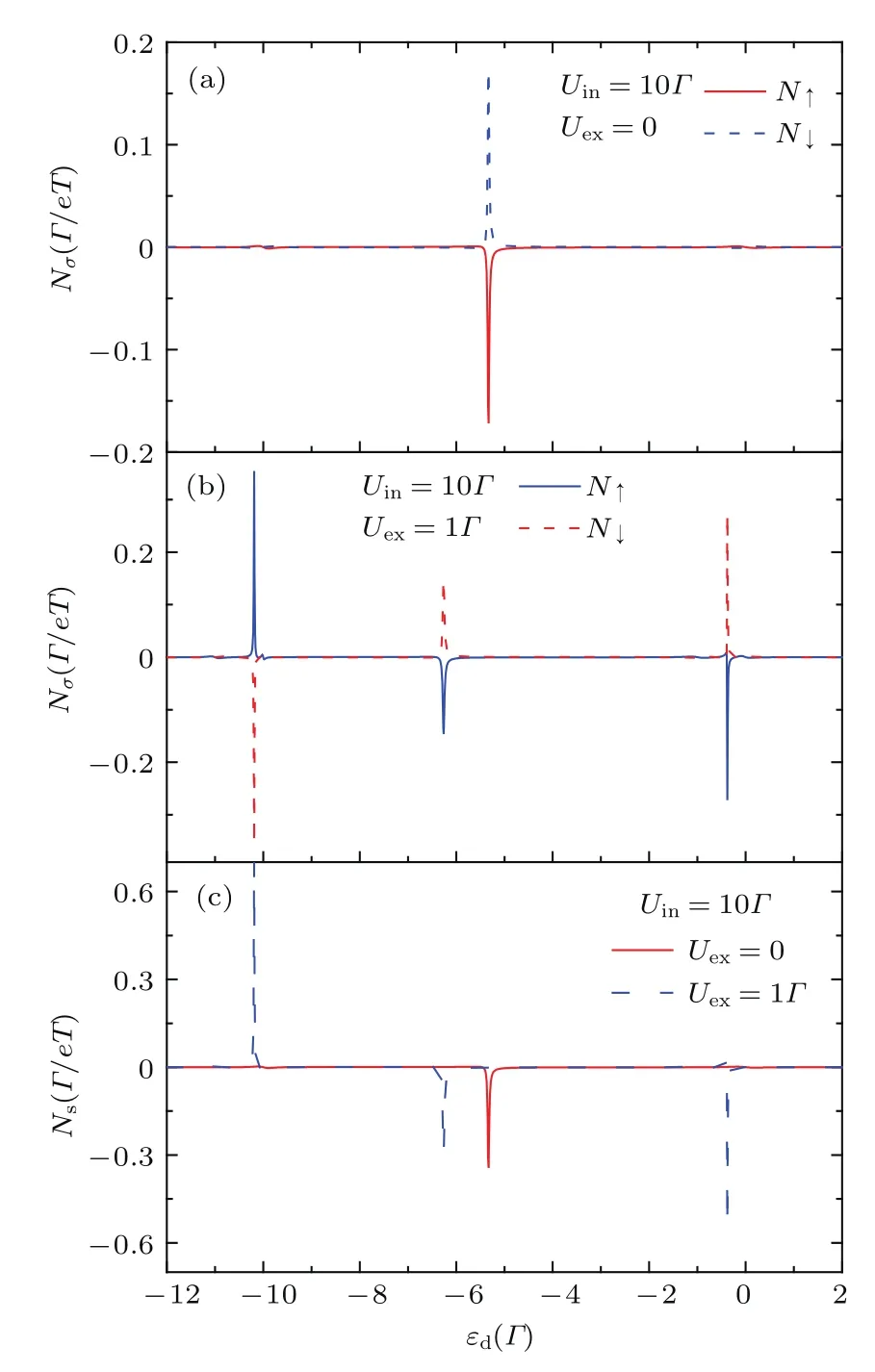
图4 (网刊彩色)电极1和电极3磁化方向反平行排列情况下,(a)Uin=10Γ,Uex=0和(b)Uin=10Γ,Uex=1Γ时自旋相关的能斯特系数Nσ随着量子点内能级εd的变化;(c)Uin=10Γ,Uex=0和Uex=10Γ时自旋能斯特系数Ns随着量子点内能级εd的变化;其他参数与图2相同Fig.4.(color online)The spin dependent Nernst coefficient Nσas a function of the dots’level εdfor antiparallel con fi guration with(a)Uin=10Γ,Uex=0 and(b)Uin=10Γ,Uex=1Γ;(c)the spin Nernst coefficient Nsas a function of the dots’level εdwith Uin=10Γ,Uex=0,and Uex=10Γ.The other parameters are the same as those of Fig.2.
4 结 论
利用非平衡格林函数方法理论研究了与四个电极耦合的双量子点系统中的自旋和电荷能斯特效应,考虑了不同电极的磁动量结构和量子点内以及量子点间电子的库仑相互作用对热电效应的影响.研究发现,当铁磁电极1和电极3中的磁化方向反平行时,电极2和电极4两端能够出现纯的自旋流或自旋偏压(纯自旋能斯特效应).把电极4从金属态转换到铁磁态时,电荷能斯特效应与自旋能斯特效应将同时出现.此外研究发现,量子点间及量子点内电子的库仑相互作用可以明显地促进能斯特效应.当库仑排斥作用存在时,自旋及电荷能斯特系数有望提高两个数量级.这样显著的特性,表明该四端口双量子点结构有望在新型热电器件的设计中具有一定的应用价值.
[1]Dubi Y,Di Ventra M 2011Rev.Mod.Phys.83 131
[2]Scheibner R,Buhmann H,Reuter D,Kiselev M N,Molenkamp L W 2005Phys.Rev.Lett.95 176602
[3]Chen X B,Duan W H 2015Acta Phys.Sin.64 186302(in Chinese)[陈晓彬,段文晖 2015物理学报 64 186302]
[4]Xu Z A,Shen J Q,Zhao S R,Zhang Y J,Ong C K 2005Phys.Rev.B72 144527
[5]Lee W L,Watauchi S,Miller V L,Cava R J,Ong N P 2004Phys.Rev.Lett.93 226601
[6]Banerjee A,Fauque B,Izawa K,Miyake A,Sheikin I,Flouquet J,Lenoir B,Behnia K 2008Phys.Rev.B78 161103
[7]Small J P,Perez K M,Kim P 2003Phys.Rev.Lett.91 256801
[8]Scheibner R,Buhmann H,Reuter D,Kiselev M N,Molenkamp L W 2005Phys.Rev.Lett.95 176602
[9]Ziese M,Thornton M J 2001Spin Electronics(New York:Springer-Verlag Press)pp396–415
[10]Fert A 2008Rev.Mod.Phys.80 1517
[11]Guo Y,Gu B L,Yoshiyuki K 2000Acta Phys.Sin.49 1814(in Chinese)[郭永,顾秉林,川添良幸2000物理学报49 1814]
[12]Seki T,Hasegawa Y,Mitani S,Takahashi S,Imamura H,Maekawa S,Nitta J,Takanashi K 2008Nature Mater.7 125
[13]Checkelsky J G,Ong N P 2009Phys.Rev.B80 081413
[14]Cyr-Choiniere O,Daou R,Laliberte F,LeBoeuf D,Doiron-Leyraud N,Chang J,Yan J Q,Cheng J G,Zhou J S,Goodenough J B,Pyon S,Takayama T,Takagi H,Tanaka Y,Taillefer L 2009Nature458 743
[15]Tauber K,Gradhand M,Fedorov D V,Mertig I 2012Phys.Rev.Lett.109 026601
[16]Cheng S G,Xing Y X,Sun Q F,Xie X C 2008Phys.Rev.B78 045302
[17]Bulka B R,Kostyrko T 2004Phys.Rev.B70 205333
[18]Sun Q F,Xing Y X,Shen S Q 2008Phys.Rev.B77 195313
[19]Jonson M,Girvin S M 1984Phys.Rev.B29 1939
[20]Oji H,Streda P 1985Phys.Rev.B31 7291
[21]Sun Q F,Xie X C 2006Phys.Rev.B73 235301
PACS:73.63.–b,72.25.–b,73.63.Kv,73.50.LwDOI:10.7498/aps.66.097302
Spin and charge Nernst e ff ect in a four-terminal double quantum dot system∗
Zheng Jun1)†Li Chun-Lei2)Yang Xi3)Guo Yong3)4)
1)(College of New Energy,Bohai University,Jinzhou 121013,China)2)(College of Elementary Education,Capital Normal University,Beijing 100048,China)3)(Department of Physics,Tsinghua University,Beijing 100084,China)4)(Collaborative Innovation Center of Quantum Matter,Beijing 100084,China)
20 December 2016;revised manuscript
20 January 2017)
With the increase of integration scale,heat dissipation becomes one of the major problems in high density electronic devices and circuits.Controlling and reusing the heat energy in such miniaturized structures are essential topics for current and future technologies.With the development of microfabrication technology and low-temperature measurement technology in the last two decades,the thermoelectric measurement in low-dimensional sample has been feasible,and the thermal transport has received more and more attention.For the multi-terminal device,there is a novel thermoelectric phenomenon,called the spin Nernst e ff ect,in which spin currents(or spin voltages)are generated perpendicularly to the temperature gradient.The spin Nernst e ff ect has been con fi rmed experimentally,and has been theoretically studied in a variety of materials.In this paper,the spin and charge Nernst e ff ect in a pair of vertically aligned quantum dots attached to four leads are studied in the Coulomb blockade regime based on the nonequilibrium Green’s function technique.We focus on the in fl uences of magnetic con fi guration and intra-dot(inter-dot)Coulomb interaction on the spin and charge Nernst e ff ect.It is found that the signs and the magnitudes of spin and charge Nernst e ff ect can be modulated by adjusting the magnetization directions of ferromagnetic electrodes.When the magnetic moments in the 1 and 3 electrodes are turned to antiparallel alignment,the pure spin Nernst(without charge Nernst)e ff ect can occur by applying a transverse temperature gradient.Conversely,the spin and charge Nernst e ff ect disappear if the magnetic moments of lead 1 and lead 3 are in the case of parallel con fi guration.Except for left and right thermal leads,we investigate the e ff ect of the middle lead(lead 4)on the property of the Nernst e ff ect.We fi nd that when the normal metal lead 4 is transferred to ferromagnetic metal,the spin and charge Nernst e ff ect both can be obtained simultaneously.In the end of the paper,we study the in fl uences of intra-dot and inter-dot Coulomb interaction on the spin dependent Nernst coefficient.Through numerical calculations,we demonstrate that the magnitude of the Nernst e ff ect is less dependent on the polarization strength of ferromagnetic electrodes,but can be remarkably enhanced by the Coulomb blockade.The spin Nernst coefficient is predicted to be more than two orders of magnitude larger than that of the case of zero Coulomb interaction.All the results indicate that the proposed four-terminal double quantum dot nano system is a promising candidate for spin caloritronic device.
quantum dot,Nernst e ff ect,Coulomb interaction
10.7498/aps.66.097302
∗国家自然科学基金(批准号:11547209,11604021,11574173)、辽宁省博士科研启动基金指导计划(批准号:201601352)、低维量子物理国家重点实验室开放课题(批准号:KF201613)和北京市教育委员会科技计划一般项目(批准号:KM201410028021)资助的课题.
†通信作者.E-mail:zhengjun@bhu.edu.cn
*Project supported by the National Natural Science Foundation of China(Grant Nos.11547209,11604021,11574173),the Doctoral Scienti fi c Research Foundation of Liaoning Province,China(Grant No.201601352),the Open Project of State Key Laboratory of Low-Dimensional Quantum Physics,China(Grant No.KF201613),and the General Program of Science and Technology Development Project of Beijing Municipal Education Commission of China(Grant No.KM201410028021).
†Corresponding author.E-mail:zhengjun@bhu.edu.cn
