微纳粒子光学散射分析

付成花

1)(中国科学院强磁场科学中心,合肥 230031)2)(中国科学技术大学,合肥 230026)

微纳粒子光学散射分析

付成花1)2)†

1)(中国科学院强磁场科学中心,合肥 230031)2)(中国科学技术大学,合肥 230026)

(2017年1月12日收到;2017年2月4日收到修改稿)

为实现利用光学方式对微纳尺度粒子性质的研究,探讨了亚微米线及亚微米球对光电磁波的散射效应.微纳米尺度粒子的光学散射,散射粒子尺寸与入射光波长尺寸可满足米氏(Mie)散射条件.利用Matlab数值模拟的方式,将分析结果以模拟图的形式清晰地展现出来.满足尺寸条件的层状粒子以及任意多个散射粒子存在时对电磁波的散射都可采用Mie散射分析方法,并且针对多粒子散射,分析了散射体位于不同位置时对散射造成的影响.通过分析光学散射光场相关的微分散射截面及近场散射电磁场分布,可得出散射光场随散射角度的变化趋势,以及散射光场受各类因素的影响,包括入射光偏振态、散射粒子尺寸、散射粒子结构及粒子构成层数、散射粒子数量等的影响,也包括一些隐含因素对散射光场的影响,如散射粒子与周围介质的相对折射率.本文的科学意义体现在:与入射光波长尺寸可比的亚微米尺度的粒子,可用作传感器,对于其位移的探测可通过光学方式来实现,而由于粒子本身特性对散射光的影响具有一定的参考价值,从而使通过光学方式对机械位移的读出具有更高准确度.研究结果对于光学方式探测亚微米线机械振动具有指导意义.

散射,尺寸可比,层状,多粒子散射

1 引 言

对于尺寸参数与光波长可比的散射粒子,可采用米氏(Mie)散射理论［1]来分析散射光场.有较多应用是基于Mie散射理论［2−4].满足尺寸条件的多种粒子均适用Mie散射,例如Mie散射理论可用于层状球体、旋转椭球体［5]、无限圆柱体或其他任意几何形状的散射.粒子对电磁波的散射［6−8]依赖于入射光波长、散射粒子尺寸以及散射体与外界的相对折射率,并且入射电磁波的偏振方向也会对散射光场产生影响［9].本文分析了球体及圆柱的散射,包括单个均匀介质单层圆柱、单个分层圆柱、多个单层圆柱、单个均匀介质圆球的散射［9−13].

实验中,考虑散射体与入射光波长尺寸的关系,用Mie散射(Mie scattering)理论来描述散射光场.Mie散射理论［1]由德国物理学家Gustav Mie提出,是球形粒子散射电磁辐射的一个完整的麦克斯韦方程组的解析解［9],描述了一种电磁平面波由均匀球体引起的散射,用无穷级数表达解的形式.微粒对电磁辐射的吸收与散射和粒子的线度有密切关系.Mie散射理论主要用于亚微米至微米尺度.Mie散射的散射场强度随散射角变化,内部场强随粒子半径变化.Mie解也用于解层状球体,旋转椭球体,无限圆柱体或其他几何形状散射的麦克斯韦方程.Mie散射可适用于任意尺寸参数的散射粒子,但一般用于与光波长可比的情况.

2 散射基本原理

散射光场的描述涉及散射角度,并且还与入射光方向及偏振态有关.这里,定义坐标系统如下:直角坐标系坐标原点O,圆柱轴线与x坐标轴重合或平行.本文只考虑入射光垂直圆柱轴线入射的情况,入射光入射方向沿z轴正方向,以平面波形式入射到散射表面.入射电磁波电场方向沿x轴方向,即偏振方向平行于散射体圆柱轴向,称之为横磁(transverse magnetic,TM)波.同理,对于入射光电磁波,其电场方向垂直于散射圆柱体轴线方向的则称之为横电(transverse electric,TE)波.描述散射光方向的参数为散射角度,定义为散射光方向偏离入射方向的角度,即散射光线与z轴正方向的夹角.经微米圆柱散射体散射之后的光波将以柱面波的形式向外传输.描述散射光的一个重要参数即散射系数,下面列出了单根单层圆柱及分层圆柱散射系数的推导公式,计算散射系数过程中涉及无穷级数的求和,其阶数n满足取值范围0到M,即n=[0,M],这里,M为计算截断数,可表示为M=α+4α1/3+2,其中α为尺寸参数,表示为α=k×r,并且这里r为散射圆柱体半径,k=(2π/λ)nm为波数,λ为入射光波长,nm为周围介质折射率.引入一个数值m,表示相对折射率,记作m=ns/nm,为散射粒子折射率(ns)与外部周围介质折射率(nm)的比值.则单根单层无限长均匀介质圆柱的散射系数可表示为

式中,Jn和J′n为第一类贝塞尔函数及其一阶导数;Hn与H′n为第三类贝塞尔函数及其一阶导数;n,α,m分别表示计算阶数、散射粒子尺寸参数、相对折射率.可以看出,对于单根单层无限长均匀介质圆柱,其散射系数依赖于n,α及m,而根据前面参数之间相互关联的介绍,可以得出n,α对散射系数的影响均可等效为散射圆柱体半径r和入射光波长λ的影响.于是我们列出散射系数an,bn与参数之间所满足的依赖关系为(an,bn)∝ [m,r,λ],即与相对折射率m、圆柱半径r、入射光波长λ有关.入射光偏振态将对振幅散射函数产生影响,TM 入射时,振幅散射函数记作T1(θ), 表达式为TE入射时则振幅散射函数记作T2(θ),表达式为微分散射截面可用来描述远场散射光场分布,入射偏振态不同将对散射截面产生影响,分别记作dCsTM与dCsTE,TM入射微分散射截面表示为TE入射则为所以对于单根单层无限长均匀介质圆柱,影响其微分散射截面的因素包含散射角度θ、圆柱半径r、相对折射率m、入射光波长λ以及入射光偏振态.而对于单根分层无限长介质圆柱的散射,其散射系数则相对复杂一些,可由(3)和(4)式表示.并且有散射粒子尺寸参数αi=2πnmri/λ,αi为每层对应的尺寸参数;N为层数,则有取值范围i=[1,N];无穷级数n的截断数表示最内层尺寸参数,αN表示最外层尺寸参数,则有阶数n=[0,M].计算过程的辅助矢量P,Q均为矩阵,其维度2N×2N,且矩阵元素下角标表示为s,t,并且有取值范围s=[1,2N],t=[1,2N].矩阵元用pst,qst表示,则矩阵可以表示为P=[pst]2N×2N,Q=[qst]2N×2N.我们在分析计算过程中假设参数w,v均用于表示多层圆柱体的由内向外第几层,即轴心表示第1层,参数取值为1,最外层表示第N层,参数取值为N.

当s=1,t=1,w=1,v=1时,pst=J′n(mw×αv),qst=mw×pst;

当s=1,t=2,w=2,v=1时,pst=J′n(mw×αv),qst=mw×pst;

当s=1,t=3,w=2,v=1时,pst=Y′n(mw×αv),qst=mw×pst;

当s=2,t=1,w=1,v=1时,qst=Jn(mw×αv),pst=mw×qst;

当s=2,t=2,w=2,v=1时,qst=Jn(mw×αv),pst=mw×qst;

当s=2,t=3,w=2,v=1时,qst=Yn(mw×αv),pst=mw×qst;

当s=2N−3,t=2N−4,w=N−1,v=N−1且N ≥3时,pst=J′n(mw×αv),qst=mw×pst;

当s=2N−3,t=2N−3,w=N−1,v=N−1且N ≥3时,pst=Yn(mw×αv),qst=mw×pst;

当s=2N−3,t=2N−2,w=N,v=N−1且N ≥3时,pst=J′n(mw×αv),qst=mw×pst;

当s=2N−3,t=2N−1,w=N,v=N−1且N ≥3时,pst=Y′n(mw×αv),qst=mw×pst;

当s=2N−2,t=2N−4,w=N−1,v=N−1且N ≥3时,qst=Jn(mw×αv),pst=mw×qst;

当s=2N−2,t=2N−3,w=N−1,v=N−1且N ≥3时,qst=Yn(mw×αv),pst=mw×qst;

当s=2N−2,t=2N−2,w=N,v=N−1且N ≥3时,qst=Jn(mw×αv),pst=mw×qst;

当s=2N−2,t=2N−1,w=N,v=N−1且N ≥3时,qst=Jn(mw×αv),pst=mw×qst;

当s=2N−1,t=2N−2,w=N,v=N时,pst=J′n(mw×αv),qst=mw×pst;

当s=2N−1,t=2N−1,w=N,v=N时,pst=Y′n(mw×αv),qst=mw×pst;

当s=2N−1,t=2N,w=N+1,v=N时,pst=J′n(αv),qst=pst;

当s=2N,t=2N−2,w=N,v=N时,qst=Jn(mw×αv),pst=mw×qst;

当s=2N,t=2N−1,w=N,v=N时,qst=Yn(mw×αv),pst=mw×qst;

当s=2N,t=2N,w=N+1,v=N时,qst=Jn(αv),pst=qst.

这里,Jn和J′n为第一类贝塞尔函数及其一阶导数;Yn与Y′n为第二类贝塞尔函数及其一阶导数. 并且,矩阵P,Q其他的剩余元素取零. 取矩阵M1=[m1st]2N×2N,与P矩阵维度相同并且各元素相等,替换其中两个矩阵元素m12N−1,2N=H′n(αN);m12N,2N=Hn(αN).并取矩阵行列式,记作det(P)和det(M1).同理,取矩阵M2=[m2st]2N×2N,与Q矩阵维度相同并且各元素相等,替换其中两个矩阵元素m22N−1,2N=H′n(αN);m22N,2N=Hn(αN).Hn与H′n为第三类贝塞尔函数及其一阶导数.并取矩阵行列式,记作det(Q)和det(M2),则多层粒子散射系数可表示为

所以,对于单根分层无限长介质圆柱其散射系数存在依赖关系(asn,bsn)∝ [r,m,N,λ],其中,r为散射圆柱半径,m为相对折射率,N为散射体圆柱构成层数,λ为入射光波长.因此圆柱层数将对散射系数产生影响.

多根圆柱散射其散射光场与散射粒子个数及相对位置有关.圆柱轴向均沿x方向,第j根圆柱在空间所处的位置可以表示为[dj,angj],其中dj与angj分别表示圆柱空间位置相对于坐标原点的距离及相对于参考坐标轴(z轴)的角度,j用于区分各个位置,且取值范围j=[1,L],L为圆柱个数,L≥2.多根圆柱散射系数amnj,bmnj由(5)和(6)式表示,并且式中n,k具有与之前相同的意义,an,bn为单根单层圆柱散射系数:

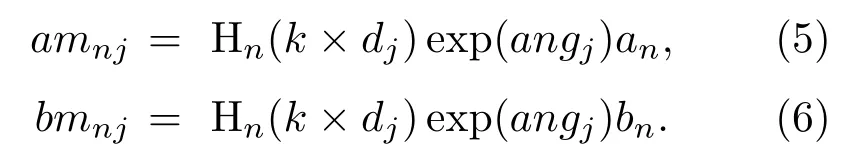
于是,多根圆柱存在时圆柱个数L及其在空间的分布dj,angj将对散射光产生影响.而空间的分布等效到yz平面上以y和z坐标的形式表示,存在关系yj=djsin(angj),zj=djcos(angj).所以,对于多根圆柱散射,其散射系数的依赖关系满足(amnj,bmnj)∝ [r,m,L,λ,yj,zj].

综合上述,根据单根单层无限长均匀介质圆柱、单根分层无限长介质圆柱及多根无限长单层介质圆柱的散射系数,并结合散射矩阵及微分散射截面的计算公式,可以得出影响微分散射截面的因素,包括散射角度θ、圆柱半径r、相对折射率m、圆柱构成层数N、入射光波长λ及偏振态(TM或TE),以及对于多根圆柱存在时圆柱个数L及其在空间的分布yj,zj.

分析近场散射电磁场可以清楚地看出近场散射光场的分布,由于篇幅有限,对于公式的详细推导这里不再赘述,本文简单列出依赖关系如下.与近场散射电场矢量和磁场矢量相关的参数可表示为(E,H) ∝ [an,bn,r,ns,nm,λ,zj,yj,xf,yf,zf],矢量(E,H)对应(Ex,Ey,Ez,Hx,Hy,Hz),其中,zj,yj表示散射圆柱体在yz平面所处位置;xf,yf,zf表示散射点位置坐标,不同点对应散射光振幅与方向均不同,f取值范围取决于空间选取点的个数,比如下文涉及的模拟计算所采用的点的个数为100.并且,根据前文对散射系数an与bn的分析可得,散射光场还应该与散射角度θ、圆柱半径r、相对折射率m以及层数N有关.因此,影响近场散射电磁场分布的因素包括圆柱半径、相对折射率、圆柱构成层数、入射光波长以及多根圆柱存在时其在空间的分布.散射光场在空间并不是均匀分布的,不同位置点将获取不同的散射光.

散射粒子形状不同所产生的散射光场分布也会不同.如果散射粒子为均匀介质球体,散射光波将以球面波的形式向外传播.不改变入射条件,即与圆柱散射采用相同的入射条件.以平面波形式入射到球体表面,散射体球心与直角坐标系原点重合,入射方向沿z坐标轴正向,入射偏振方向沿x轴方向称之为平行,记作“//”,偏振方向沿y轴方向称之为垂直,记作“⊥”.对于球体的散射也有类似的推导过程.为比较散射体形状对散射光场的影响,我们分析比较了单个单层均匀球体对平面波的散射与单根单层无限长均匀介质圆柱对平面波的散射.

影响散射光场的因素还涉及球体尺寸、相对折射率、入射光波长及偏振态,并且单层球体与层状球体也会有不同的散射系数及散射光场分布.对于圆球散射的推导,我们简单列出了各影响因素以便分析.影响散射光的一个重要参数——振幅散射函数可以表示为S//,⊥(θ,an,bn),其中下角标“//”或“⊥”用于区分不同入射光偏振态条件下的振幅散射函数;an,bn为散射系数.注意,对于单个单层散射球体,这里取散射系数an,bn,同时散射系数依赖于入射光波长λ、散射体半径r、散射体与周围介质的相对折射率m;而散射球体层数≥2或散射球体个数≥2时则取不同形式散射系数,这两种情况与圆柱散射有类似的推导,不再赘述.不同的入射偏振态,对应散射系数不同,并且振幅散射函数S不同(取S//或S⊥).此外,振幅散射函数S还与散射角度θ相关,散射角度的定义是散射光方向偏离入射光方向的角度,也就是散射光方向与z轴正方向的夹角.电场平行于z轴入射时微分散射截面为电场垂直于x轴入射时微分散射截面为球体散射其近场散射矢量电磁场存在依赖关系(E,H) ∝ (r,λ,m,N,xf,yf,zf),(E,H)矢量对应(Ex,Ey,Ez,Hx,Hy,Hz),散射场位置点坐标(xf,yf,zf),f取值范围取决于空间选取点的个数.

可以看出,影响近场散射电磁场分布的因素包括粒子尺寸与构成(形态)层数、散射粒子与外部介质的相对折射率、入射光波长及偏振态、散射角度以及多粒子散射时粒子在空间所处的位置.并且以平面波入射的光场经散射之后空间光场不再呈均匀分布的状态,在不同位置可探测的散射光振幅级强度不同.并且不同形状下散射体的散射光场也不同,本文通过无限长介质圆柱与介质球体的散射对比进行了研究.

3 实验模拟结果

3.1亚微米线圆柱光学散射

根据前面已定义的坐标系统,入射光以平面波形式入射到圆柱表面.圆柱轴线沿坐标系x轴方向,光线入射方向沿z轴正方向,入射光可为TM和TE偏振态.散射光以柱面波形式向外传播且与散射体圆柱轴线重合［1].模拟实验所采用入射光波长(真空)均为1.55µm.下图1—图6分析了不同微米线圆柱在相同入射条件下所产生的散射光场,取圆柱半径Rc=0.92µm和Rc=0.61µm,通过比较这两种尺寸下远场微分散射截面及近场电磁场分布来分析散射粒子尺寸对散射光场的影响.

图1 (网刊彩色)半径为0.92µm的单根无限长单层均匀介质圆柱近场散射电磁场Fig.1. (color on line)Near- fi eld distribution of the light scattered by a single in fi nite-length mono-layer homogeneous dielectric cylinder with a 0.92µm radius.

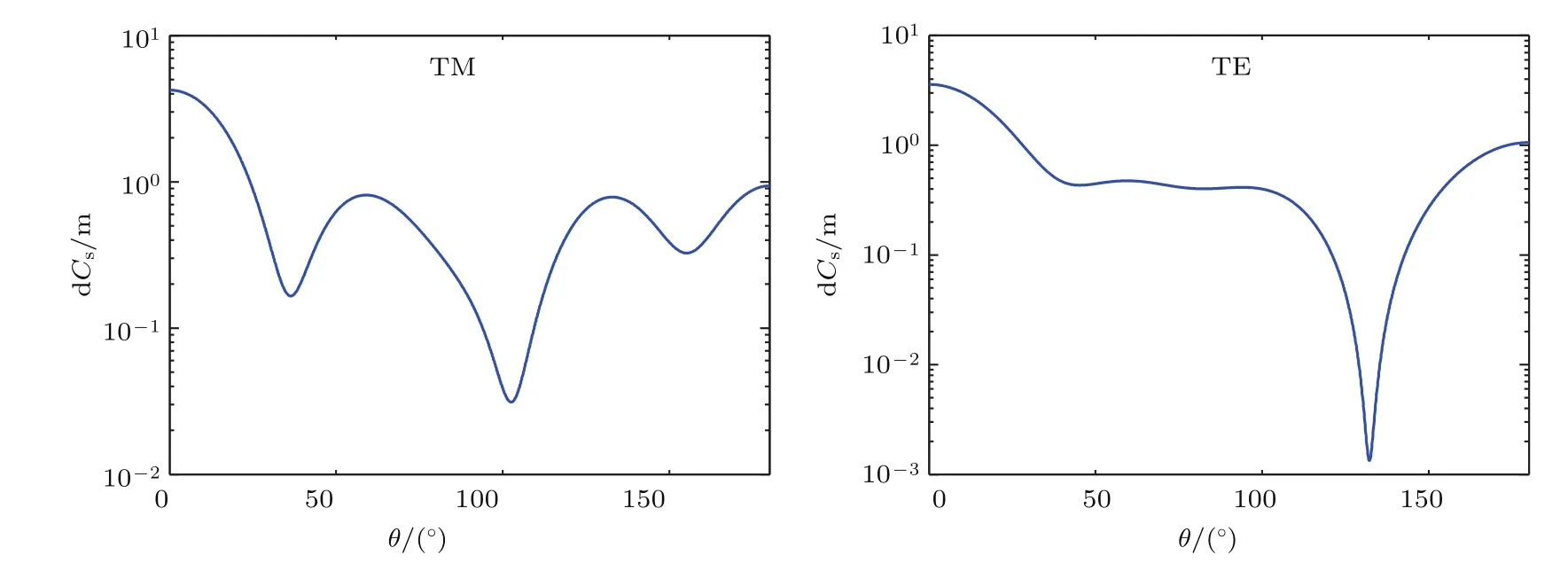
图2 半径为0.92µm的单根无限长单层均匀介质圆柱微分散射截面,做图范围半平面,即提取散射角度范围[0◦,180◦]Fig.2.Di ff erential scattering cross section of a single,in fi nite-length,mono-layer and homogeneous dielectric cylinder with a radius of 0.92 µm,the drawing scope is a half-plane,that is,taking the scattering range of[0◦,180◦].

图3 (网刊彩色)半径为0.61µm的单根无限长单层均匀介质圆柱近场散射电磁场Fig.3.(color on line)Near- fi eld distribution of the light fi eld scattered by a single in fi nite-length mono-layer homogeneous dielectric cylinder with a radius of 0.61µm.

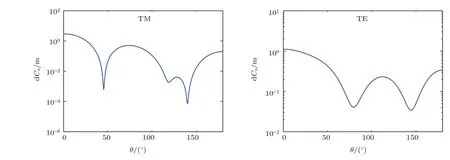
图4 半径为0.61µm的单根无限长单层均匀介质圆柱微分散射截面,做图范围半平面,即提取散射角度范围[0◦,180◦]Fig.4.Di ff erential scattering cross section of a single,in fi nite-length,mono-layer and homogeneous dielectric cylinder with a radius of 0.61 µm,the drawing scope is a half-plane,that is,taking the scattering range of[0◦,180◦].

图5 (网刊彩色)最外层半径为0.92µm的单根无限长分层介质圆柱近场散射电磁场,圆柱层数为5层Fig.5. (color on line)Near- fi eld distribution of the light fi eld scattered by a single in fi nite-length 5-layer dielectric cylinder with the outermost radius of 0.92µm.

图6 最外层半径为0.92µm的单根无限长5层介质圆柱微分散射截面Fig.6. Di ff erential scattering cross section of a single in fi nite-length 5-layer dielectric cylinder with the outermost radius of 0.92µm.

图1和图3描述单根无限长单层均匀介质圆柱近场散射电磁场分布,其子图选取的范围y与z方向均为[−4Rc,4Rc],横、纵坐标轴的数字仅表示选取坐标点的个数为100.图2和图4表示不同散射圆柱体尺寸条件下的微分散射截面［10],两幅图中横坐标均表示散射角度,范围标注[0◦,180◦],纵坐标表示微分散射截面对数值.单根无限长均匀介质圆柱所产生的散射光场关于垂直入射的光线呈对称分布,即散射光场关于z轴对称,所以散射角度提取范围[0◦,180◦]足以描述该条件下微分散射截面的变化趋势.图1和图2散射体圆柱尺寸Rc=0.92µm,且入射光选取TM入射.图3和图4对应Rc=0.61µm.图1与图3的比较可以明显地看出不同尺寸散射圆柱体所产生的散射电磁波矢量不同,从近场角度分析电场及磁场各个方向的分量;而图2与图4则是从远场角度观察散射光场,对散射之后的光场从整体上进行分析.通过图1—图4,可以得出散射粒子尺寸对散射光的影响.而对于具有相同尺寸不同构成形态的圆柱体所产生的散射光场,则可以通过图5、图6与图1和图2的比较来进行分析.图5和图6对应的圆柱构成分为5层,层数与半径及折射率一一对应,每层对应不同的折射率,最外层半径为0.92µm,与图1和图2中单层均匀介质圆柱具有相同的尺寸.

多根相同尺寸的无限长均匀介质圆柱,轴向均平行于x坐标轴方向,放置于yz平面不同的坐标点位置,光线同样沿z轴正向垂直入射于圆柱表面,且多根圆柱均处于光束直射区域,产生散射光场［11,14].图7—图10描述了三根半径均为0.92µm的圆柱同时放置于空间不同位置时的散射光场分布.首先,将三根圆柱分别放置于yz平面,坐标值为zc=[0,0,1.6]×2Rc,yc=[1.6,−1.6,0.1]×2Rc的位置,这样垂直平面入射光经这三根圆柱散射之后的电磁场分布如图7所示,并且从远场观测经多粒子散射之后的微分散射截面如图8所示.在图8中横坐标散射角度标注范围为[0◦,360◦],由多根圆柱的任意空间位置导致多重散射之后的微分散射截面不再关于入射光方向呈对称分布.改变上述三根圆柱的空间位置,其在yz平面的位置变为zc=[0,0.5,1.0]×2Rc,yc=[0,−1.5,0]×2Rc,同样入射条件下产生的散射光场由图9和图10表示,且分别描述了近场散射电磁场及远场微分散射截面.

图7 (网刊彩色)半径相同的三根无限长单层均匀介质圆柱同时存在于空间光束照射区时所产生的近场散射电磁场分布,其中,圆柱半径Rc=0.92µm,所处yz平面坐标值zc=[0,0,1.6]×2Rc,yc=[1.6,−1.6,0.1]×2RcFig.7.(color online)Near- fi eld distribution of the light fi eld caused when three in fi nite-length mono-layer homogeneous dielectric cylinder with the same radius coexist in the spatial beam irradiating region.The radius Rcis equal to 0.92 µm,and positions in the yz plane are zc=[0,0,1.6]×2Rc,yc=[1.6,−1.6,0.1]× 2Rc.

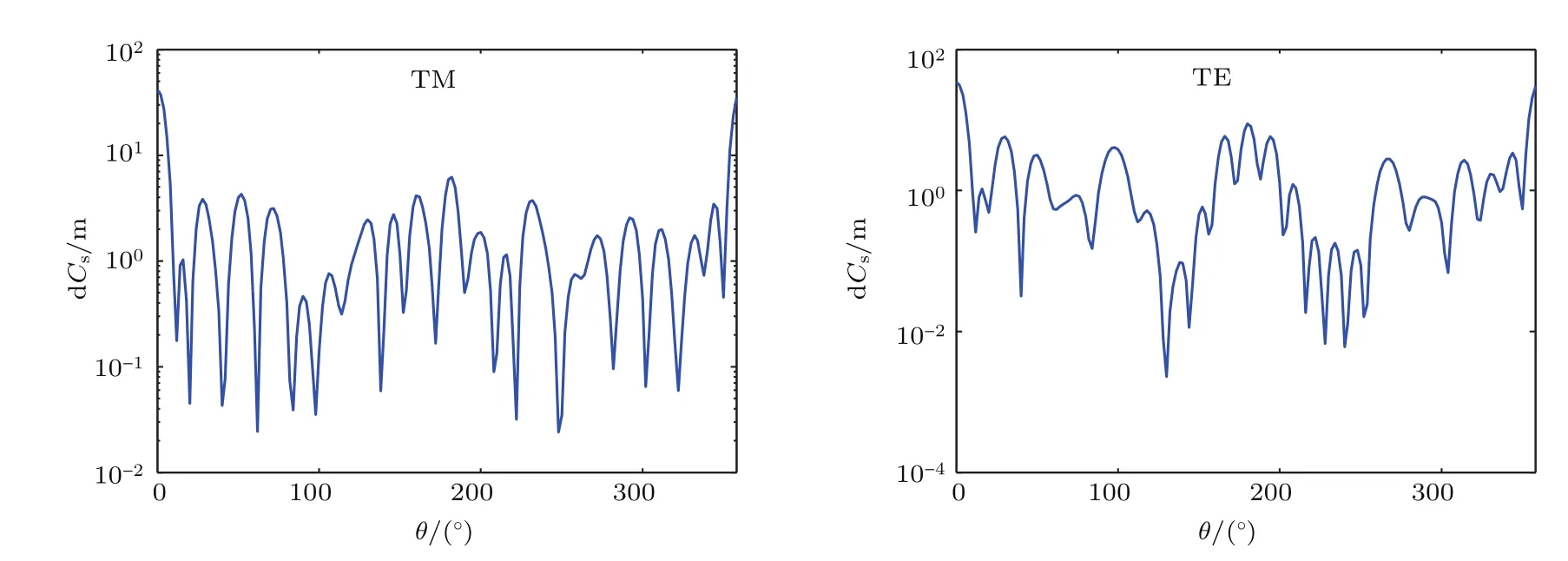
图8 半径相同的三根无限长单层均匀介质圆柱同时存在于空间光束照射区时所产生的远场微分散射截面,其中,圆柱半径Rc=0.92µm,所处yz平面坐标值zc=[0,0,1.6]×2Rc,yc=[1.6,−1.6,0.1]×2RcFig.8.Far- fi eld di ff erential scattering cross section caused when three in fi nite-length mono-layer homogeneous dielectric cylinder with the same radius coexist in the spatial beam irradiating region.The radius Rcis equal to 0.92 µm,and positions in the yz plane are zc=[0,0,1.6]×2Rc,yc=[1.6,−1.6,0.1]×2Rc.

图9 (网刊彩色)半径相同的三根无限长单层均匀介质圆柱同时存在于空间光束照射区时所产生的近场散射电磁场分布,其中,圆柱半径Rc=0.92µm,所处yz平面坐标值zc=[0,0.5,1.0]×2Rc,yc=[0,−1.5,0]×2RcFig.9.(color online)Near- fi eld distribution of the light fi eld caused when three in fi nite-length mono-layer homogeneous dielectric cylinder with the same radius coexist in the spatial beam irradiating region.The radius Rcis equal to 0.92 µm,and positions in the yz plane are zc=[0,0.5,1.0]×2Rc,yc=[0,−1.5,0]×2Rc.

图10 半径相同的三根无限长单层均匀介质圆柱同时存在于空间光束照射区时所产生的远场微分散射截面,其中,圆柱半径Rc=0.92µm,所处yz平面坐标值zc=[0,0.5,1.0]×2Rc,yc=[0,−1.5,0]×2RcFig.10.Far- fi eld di ff erential scattering cross section caused when three in fi nite-length mono-layer homogeneous dielectric cylinder with the same radius coexist in the spatial beam irradiating region.The radius Rcis equal to 0.92 µm,and positions in the yz plane are zc=[0,0.5,1.0]×2Rc,yc=[0,−1.5,0]×2Rc.

以上描述均针对散射粒子形态为无限长介质圆柱,如果散射体形状改变,散射光场将会发生怎样的变化?为研究散射粒子形状对散射光场的影响,我们选取具有与上述圆柱相同半径的球体,在相同入射条件下模拟其散射光场.

3.2亚微米球体光学散射

类似于前面对圆柱散射的分析,对与入射光波长尺寸可比的圆球散射进行分析［15−20].入射光方向沿z轴正方向,散射球体球心位于直角坐标系原点,描述散射光方向的散射角度定义为散射光线与z轴正向之间的夹角.平面波入射到均匀介质球体表面被散射,散射光将以球面波的形式向外传播,球面波球心与散射球体球心重合,则散射角度范围为环绕球体一周的[0◦,360◦].图11和图12为散射圆球球体半径Rs=0.92µm条件下模拟所得散射光场,分别表示近场散射矢量电磁场在各坐标方向的投影分量以及微分散射截面随散射角度的变化趋势.且散射光场关于入射光线对称,即关于z坐标轴呈对称分布,因此在微分散射截面的描述中,做图范围标注[0◦,180◦]即可.

图11和图12中将半径Rs=0.92µm的散射球体放置于直角坐标系原点,球心与坐标原点重合,并且坐标原点也作为散射球面波的球心来探测微分散射截面随角度的分布,如图12所示.图11描述该球体散射的近场电磁场分布.

所以,可以得出入射光偏振态、散射粒子尺寸、散射粒子结构及粒子构成层数、散射粒子数量等影响电磁波散射的物理机制:入射光偏振态对散射系数有影响,从而对振幅散射函数产生影响,导致散射光场在不同偏振态下不同,并且一般TM波入射所产生散射光场强度将大于TE波入射情况;散射系数有关的参数为尺寸参数,该尺寸参数与粒子尺寸,入射光波长及粒子与外部介质的相对折射率有关,粒子尺寸对散射光场的影响并不是单调变化的,并且可能在某一个尺寸条件下对应某一散射角度方向其散射光场将呈现最大值,这就需要根据实际试验情况来确定选取怎样的散射粒子尺寸;散射粒子构成层数及散射粒子数量对散射光场的影响并不呈单调变化趋势.

图11 (网刊彩色)半径Rc=0.92µm的单个单层均匀介质球体近场散射电磁场Fig.11.(color online)Near- fi eld distribution of the light fi eld scattered by a single mono-layer homogeneous dielectric sphere with a 0.92µm radius.

图12 半径为0.92µm的单个单层均匀介质球体微分散射截面,做图范围半平面,即提取散射角度范围[0◦,180◦]Fig.12.Di ff erential scattering cross section of a single mono-layer dielectric sphere with a radius of 0.92µm,the drawing scope is a half-plane,that is,taking the scattering range of[0◦,180◦].

4 结 论

通过以上TM与TE偏振态入射条件下的微分散射截面可以看出,相同圆柱,以相同入射光强、相同入射方向、不同偏振方向垂直入射,产生的散射光场将不同.因此,入射光的偏振方向将影响散射光场分布.并且,微分散射截面是散射角度的函数,不同散射方向对应散射光振幅不同.单根圆柱独立散射其散射截面呈对称分布,即入射光线两侧散射光场呈现轴对称分布.并且,由单根分层圆柱的远场散射截面及近场散射电磁波分布的描述可以看出,半径相同层数不同将产生不同的散射光场,但其对称性仍存在.散射体尺寸及形态均对散射光场产生影响.相同的入射条件、不同的散射体尺寸及形态将产生不同的散射光场.多根圆柱同时散射,受圆柱任意位置的影响,所有圆柱总体散射的光场关于入射光线轴对称性可能被破坏,如果多粒子位置关于入射光线对称,则其散射光场对称性仍保持关于入射光线的轴对称性.

通过对亚微米线圆柱及亚微米球体的光学Mie散射分析可以清楚地看出,与入射光波长可比尺寸的粒子对电磁波的散射分布,并且分析得出影响散射光场分布的各种因素,包括入射光偏振方向、散射粒子尺寸、散射粒子构成(层数)以及散射粒子个数.并且散射光场为散射角度的函数,各散射方向对应不同的散射光场.此外,一些隐含因素也对散射光场产生影响,如散射粒子折射率与外界环境折射率及二者之间的相对折射率.本文同时分析了圆柱散射与球体散射,可以看出散射粒子形状也是影响散射光场分布的重要因素,无限长介质圆柱对平面入射波的散射呈柱面波形式,而介质球体则以球面波的形式向外传播.虽然本文只是针对亚微米尺寸的粒子进行Mie散射分析,并且Mie散射理论主要用于亚微米至微米尺度,而实际Mie散射理论可适用于任意尺寸粒子的散射,所以类似的散射分析可用于更广泛的研究中.

感谢中国科学院强磁场科学中心薛飞研究员提供的科研环境与资金支持,及其对作者的指导与帮助.

[1]van de Hulst H C 1981Light Scattering by Small Particles(Vol.1)(New York:Dover)pp119–130

[2]Zhang Q X,Li Y D,Deng X J,Zhang Y M 2011Acta Phys.Sin.60 084216(in Chinese)[张启兴,李耀东,邓小玖,张永明2011物理学报60 084216]

[3]Qian K Y,Ma J,Fu W,Luo Y 2012Acta Phys.Sin.61 204201(in Chinese)[钱可元,马骏,付伟,罗毅 2012物理学报61 204201]

[4]Ou J,Jiang Y S,Shao Y W,Qu X S,Hua H Q,Wen D H 2013Acta Phys.Sin.62 114201(in Chinese)[欧军,江月松,邵宇伟,屈晓声,华厚强,闻东海2013物理学报62 114201]

[5]Jones R C 1945Phys.Rev.68 93

[6]Stratton J A 1941Electromagneic Theory(New York:McGraw-Hill Book Co.)pp349–420

[7]Mie G 1908Ann.Phys.330 377

[8]Chu C M,Churchill S W 1955J.Opt.Soc.Am.45 958

[9]Wiscombe W J 1980Appl.Opt.19 1505

[10]Bohren C F,Hu ff man D R 2004Absorption and Scattering of Light by Small Particles(Weinheim:Wiley-Vch Verlag GmbH Co.KGaA)pp130–154

[11]Lee S C 1990J.Appl.Phys.68 4952

[12]Kerker M 1969The Scattering of Light and Other Electromagnetic Radiation(London:Academic Press)pp255–268

[13]Bruno A B,Brauer J R 1988J.Appl.Phys.63 3200

[14]Chandrasekhar S 1960Radiative Transfer(New York：Dover Publications Inc.)pp393–399

[15]Mores P M,Feshbach H 1953MethodsofTheoretical Physics(New York:McGraw-Hill Book Co.)pp1130–1131

[16]Bechelany M,Brioude A,Cornu D,Ferro G,Miele P 2007Adv.Funct.Mater.17 939

[17]Brönstrup G,Jahr N,Leiterer C,Csáki A,Fritzsche W,Christiansen S 2010ACS Nano4 7113

[18]Lopez F J,Hyun J K,Givan U,Kim I S,Holsteen A L,Lauhon L J 2012Nano Lett.12 2266

[19]Grzela G,Hourlier D,Rivas J G 2012Phys.Rev.B86 045305

[20]Hyde M W,Bogle A E,Havrilla M J 2013Opt.Express21 32327

PACS:73.50.Bk,73.21.Ac,11.80.Jy,11.80.LaDOI:10.7498/aps.66.097301

Analysis of optical scattering of micro-nano particles

Fu Cheng-Hua1)2)†

1)(High Magnetic Field Laboratory,Chinese Academy of Sciences,Hefei 230031,China)2)(University of Science and Technology of China,Hefei 230026,China)

12 January 2017;revised manuscript

4 February 2017)

The micro-nano-scale science is rapidly developing.In order to study the properties of micro-nano-scale particles by the optical method,we discuss the scattering e ff ects of sub-micrometer wires and sub-micrometer balls on photoelectromagnetic wave in this paper.For the optical scattering of micro-nano-scale particles,the scattering particle size can meet the Mie scattering conditions compared with the incident light wavelength,that is to say,the scatterer and the incident wavelength have comparable size.In this article,the analysis results are clearly displayed in the form of simulation graphs obtained by the Matlab numerical simulation.The Mie scattering analysis method can be used for discussing the scattering of electromagnetic waves in the cases of layered particles which meet the size requirements and any number of scattering particles.Multi-particle scattering is analyzed to investigate the e ff ects of scatterers at di ff erent positions on the scattering.By analyzing the di ff erential scattering cross section and the electromagnetic fi eld distribution of near- fi eld scattering related to the scattering light fi eld,we obtain the variation trend of the scattering light fi eld with scattering angle and the e ff ects of various factors on the scattering light fi eld,including the polarization of incident wave,the size of the scatterer,the structure of scattering particles,the number of particles,the number of scattering particles,and some hidden factors such as the relative refractive index of scatterer and surrounding medium.The scienti fi c signi fi cance of the paper is re fl ected through the fact that the sub-micron scale particle can be used as a sensor of detecting the displacement,which can be realized by optical means.So it has a certain reference value for studying the in fl uence of particle own characteristic on the scattering light,thereby rendering the optical readout of the mechanical displacement very accurate.The obtained results have a guiding signi fi cance for studying the optical detection of mechanical vibrations of sub-micron wires.

scattering,comparable size,layered,multi-particle scattering

10.7498/aps.66.097301

†通信作者.E-mail:fuchenghua2014@hm fl.ac.cn

†Corresponding author.E-mail:fuchenghua2014@hm fl.ac.cn