黏性流体中超细长弹性杆的动力学不稳定性∗
2017-08-09王鹏薛纭楼智美
王鹏薛纭 楼智美
1)(济南大学土木建筑学院,济南 250022)2)(上海应用技术大学机械工程学院,上海 201418)3)(绍兴文理学院物理系,绍兴 312000)
黏性流体中超细长弹性杆的动力学不稳定性∗
王鹏1)†薛纭2)楼智美3)
1)(济南大学土木建筑学院,济南 250022)2)(上海应用技术大学机械工程学院,上海 201418)3)(绍兴文理学院物理系,绍兴 312000)
(2016年11月14日收到;2016年12月18日收到修改稿)
基于坐标基矢摄动的方法研究了黏性流体中超细长弹性杆动力学稳定性判据与失稳后的模态选择,推导出了黏性介质中超细长弹性杆Kircho ff动力学方程的一阶摄动表示,即线性的二阶偏微分方程组.以平面扭转DNA环为例,说明了以上结果的应用,得到了平面扭转DNA环的稳定性判据及其稳定的临界区域,讨论了其失稳后的模态选择及黏性阻力对其的影响.
超细长弹性杆,摄动方法,黏性流体,不稳定性
1 引 言
基于Kirchho ff弹性杆理论,Behanm[1]和Le Bret[2]建立了DNA弹性杆模型,可用于描述DNA链的几何形态和运动,并能与实验观测的结果相符合[3,4].关于DNA弹性杆力学模型的研究已取得很多重要成果[3−9].特别是随着单分子操纵技术的发展,为DNA力学的研究提供了更多的实验依据[10].
关于DNA分子模型为背景的超细长弹性杆稳定的研究已有很多工作[9,11−16].通常情况下,把Kirchho ff方程化为欧拉角表示的方程,分析静力学方程或动力学方程解的稳定性,或者通过引入扰动量研究平衡解的李雅普诺夫稳定性.但是基于以上方法实际并不能得出一致的摄动格式[17].文献[18]基于坐标基摄动给出了细长杆的一类新振幅方程,克服了周期性边界条件不连续的问题,从而无需借助欧拉角或者Lagrange方程,直接对弹性杆动力学方程进行摄动展开讨论其动力学特性,此方法下保持了杆的弧长不变.并用于研究生物的生长问题[19].
在低雷诺数下,黏性阻力和阻力矩对细胞内DNA的运动的影响将不可忽略.Klapper[20]利用数值方法讨论扭转弹性杆动力学及生物学应用.Goldstein等[21,22]研究了扭转和旋转作用下细菌纤维的黏性动力学问题,但都未对稳定性进行分析.Liu和Sheng[23]讨论了黏性介质中螺旋杆的振动与稳定性问题,但不能预测弹性杆失稳后的动力学行为.文献[17]虽然分析了纤维的动力学稳定性,却未考虑黏性项的影响.在DNA复制及转录或者生物生长过程中,黏性项对其动力学稳定性的影响引起关注[21,22],然而很少有文献涉及对其稳定性的分析,故而有必要对黏性作用下超细长弹性杆动力学的稳定性进行分析.
本文利用新的摄动方法,研究黏性流体中超细长弹性杆模型的动力学不稳定性,并以受扭转作用的封闭DNA微环为例说明结果的应用.本文采用不考虑轴向拉伸的Kirchho ff模型.本文第2部分简单介绍新的摄动格式;第3部分给出黏性流体中超细长弹性杆动力学方程的建立过程,并给出其无量纲形式;第4部分给出黏性流体中超细长弹性杆动力学方程的一阶摄动形式;第5部分将以上结果应用于分析黏性流体中平面扭转DNA环的稳定性与失稳模态选择;最后是总结.
2 摄动格式简介[18]
坐标基摄动展开的主要思想是对主轴坐标基进行任意阶摄动后仍满足正交性,即对任意阶摄动εn,满足ei.ej=δij.以一阶摄动基矢为例,可表示为

其中Aij为反对称矩阵元.将基矢量摄动展开,并利用正交条件,很容易证明上式.矩阵A的形式可以表示为
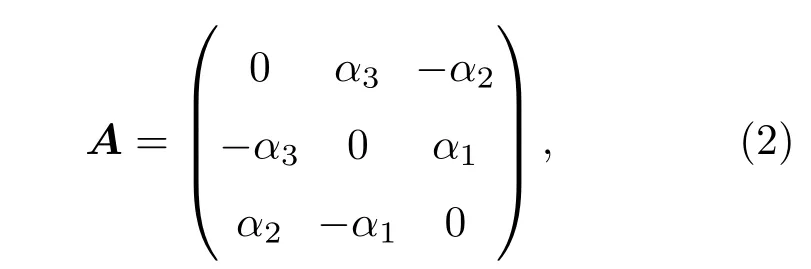
其中α为零阶任意矢量.则单位基矢量的一阶摄动展开又可以表示为
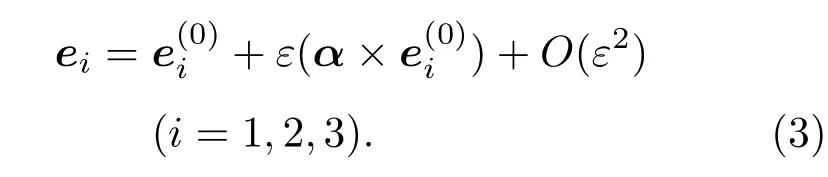
可以证明(1)式与(3)式是等价的.展开(3)式中的一阶摄动项,得到
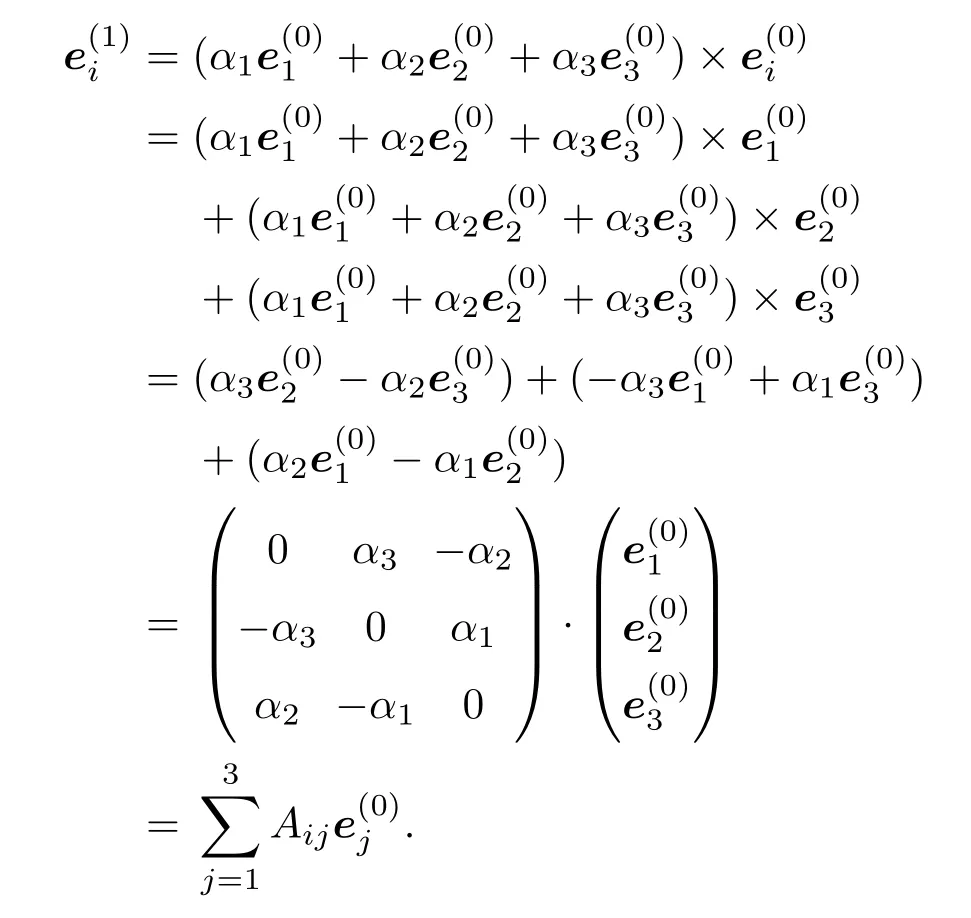
证毕.以上形式可以推广到任意阶形式.

3 动力学模型
3.1动力学方程
我们采用弹性杆的Kircho ff动力学模型.以F,M表示弹性杆截面受到的内力主矢和内力主矩.根据流体中细长体的阻力理论[24],只需考虑局域黏性阻尼,此时与杆的运动速度有关,以f,m表示黏性阻力和黏性阻力矩,其表达式为
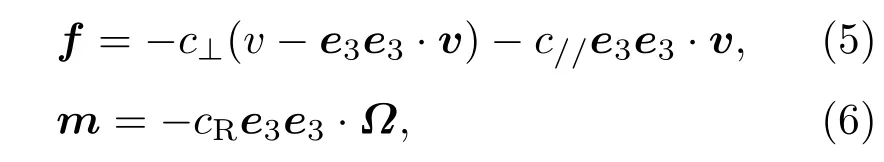
其中ei(i=1,2,3)表示主轴坐标系各轴基矢量,e3e3为并矢;v=∂r/∂t代表杆截面运动速度;c⊥,c//分别为径向和切向的介质阻力系数,cR为介质阻尼力矩系数[21,24];Ω为杆截面的角速度.考虑黏性作用后,根据动量与动量矩平衡,我们得到
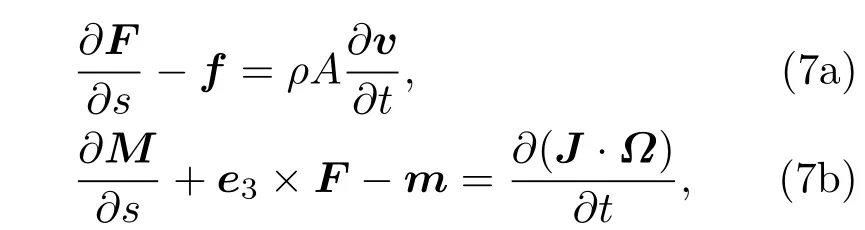
方程(7)描述了杆截面在黏性流体中的运动,其中ρ,A分别为杆的密度和杆截面面积;J是单位长度杆的惯性张量,其在截面主轴坐标系(P-xyz)中的投影矩阵以绕x,y,z轴的单位长度转动惯量Ji(i=1,2,3)为元素.
3.2坐标基表示


其中,.表示对时间求一阶偏导数,.表示对时间求二阶偏导数;ω为杆截面的弯扭度.将(9)式代入方程(7),并将方程(7a)两边同时求关于弧坐标的偏导数,我们得到方程(7)用主轴坐标基矢表示的形式:
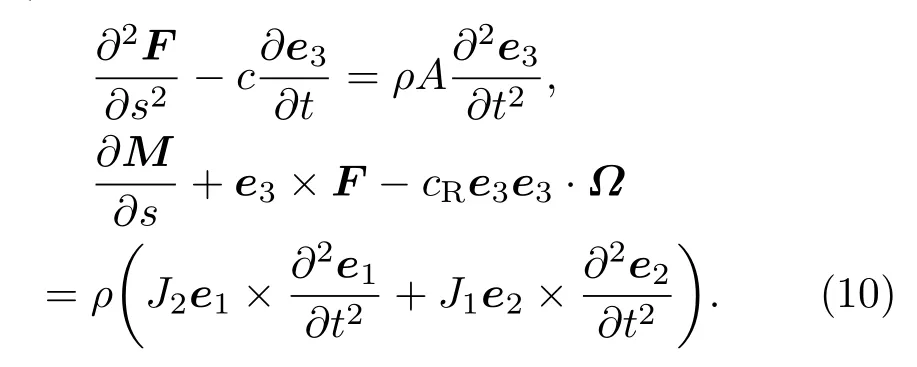
以上方程还不能完全确定超细长弹性杆的运动,为此需补充线弹性本构方程
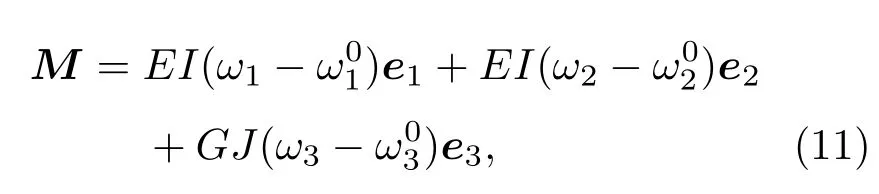
3.3无量纲式
我们将所有的量按以下关系进行重新标度,

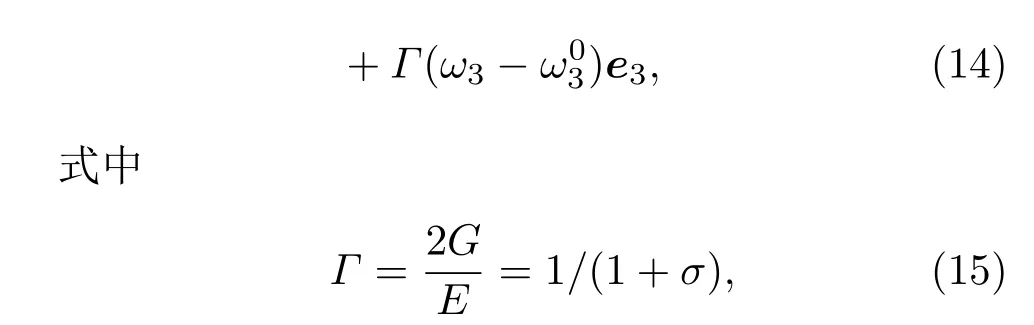
其中σ为弹性杆的泊松比.
4 一阶摄动方程
对方程(13a)的坐标基矢做一阶摄动展开,令相同阶幂次的项系数为零,忽略二阶以上项,得到零阶运动方程为
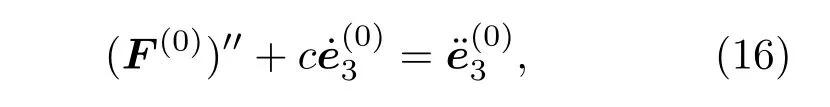
其中′′表示对弧坐标求二阶偏导.若弹性杆处于平衡态,则(16)式化为
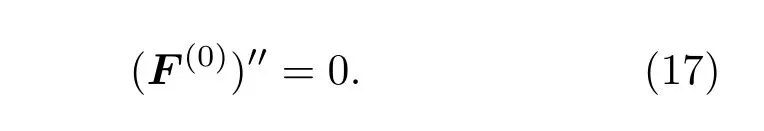
一阶摄动运动方程为

将(18)式用零阶坐标基表示为

在(19)式推导中我们利用了Ω(1)=,Ω(0)=0.将(19)式写为分量形式,得到


将方程(13b)按坐标基摄动展开为一阶摄动形式,得到
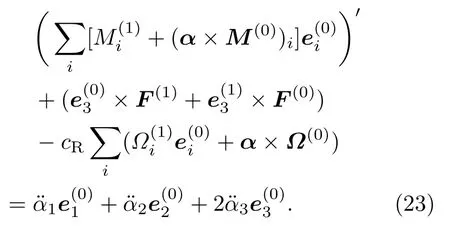
将本构方程(14)做摄动展开,得到一阶摄动形式为
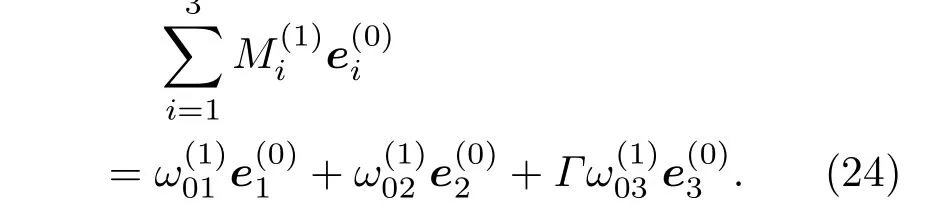
弯扭度按坐标基摄动展开的一阶形式为


把(26)式代入(25)式得

把(27)式代入(24)式,直接计算得到动量矩平衡方程的一阶摄动项在零阶各坐标轴的分量形式
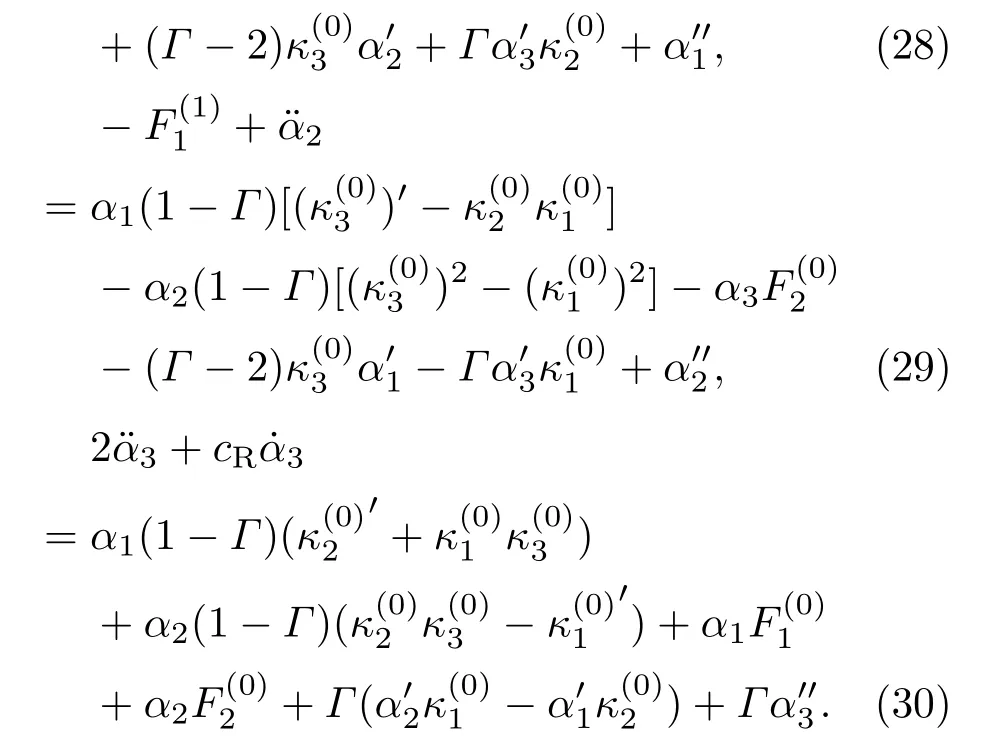
方程(20)—(22),(28)—(30)构成了黏性流体中超细长Kircho ff弹性杆的动力学变分方程.方程的解决定了弹性杆的稳定性.为了更明显地看出其线性性质,我们可以将以上方程写为以矩阵表示的二阶偏微分方程组:
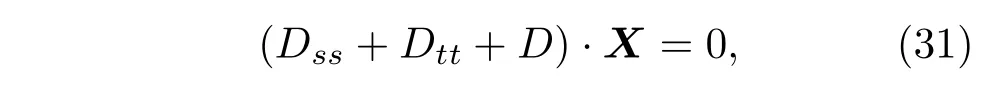
5 应 用
5.1稳定性
闭合的超细长弹性杆受到扭转作用可形成DNA超螺旋结构[3].我们将DNA微环[25]看作受到扭转作用的超细长弹性杆,其弹性模量等力学参数可由实验获得[26,27],实验中测得的DNA环抗扭刚度系数和抗弯刚度系数之比在0.5≤Γ≤1.5范围内[28],研究在此典型比值下弹性环的稳定性判据.其静态解为
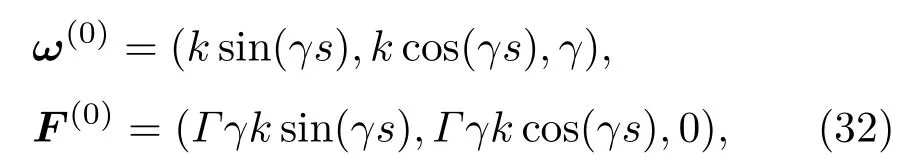
其中k为平面DNA环半径的倒数,γ为DNA环的弹性杆模型的截面的扭率,若杆的扭率为常量,则扭转数TW=γ/k.我们引入变量gi=Rγ.Xi,其中
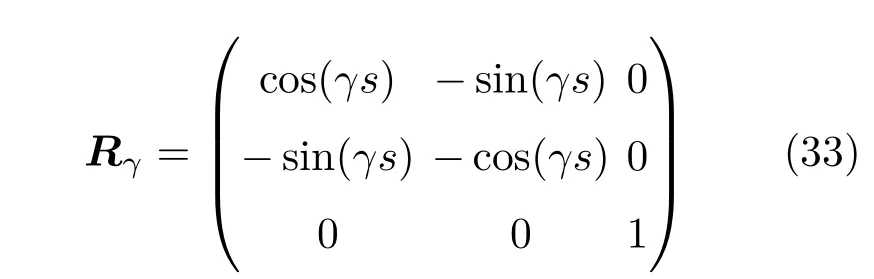
为主轴坐标向Frenet坐标投影的方向矩阵,是正交对称矩阵.此时方程(31)进一步写为
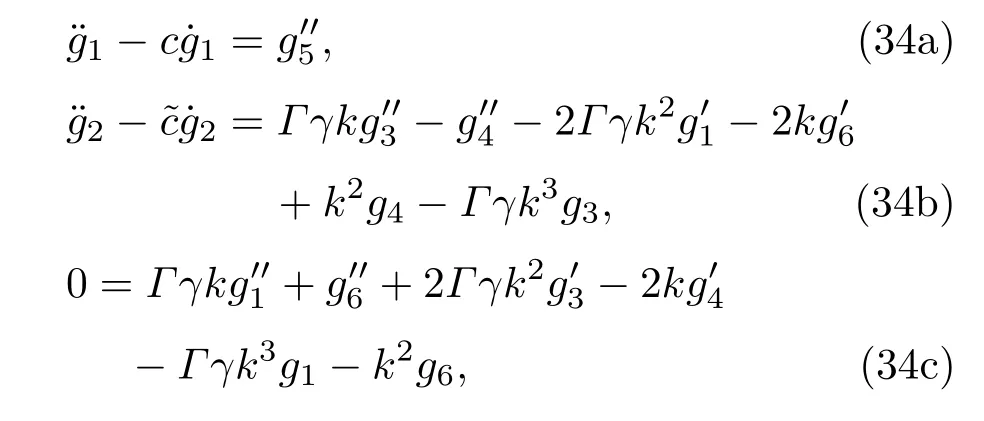

则线性方程组(36)有解.式中
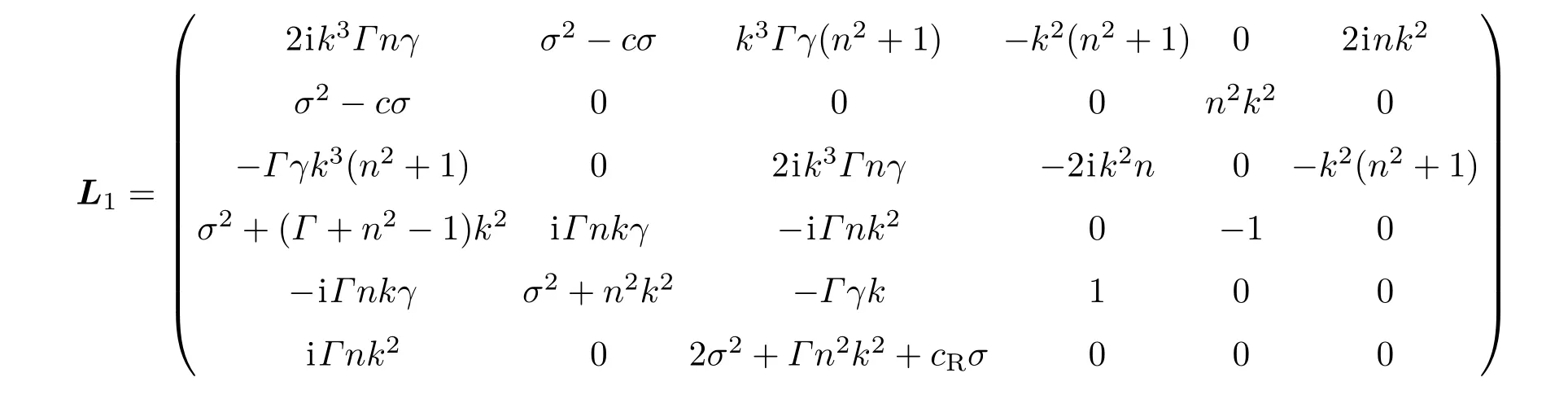
为方程(36)的系数矩阵,其中σ,n为未定参数.由封闭杆的周期性条件,n的取值为整数.平面扭转DNA环解的稳定性可根据特征值σ实部的正负确定,如果Re(σ)< 0,则解稳定,如果Re(σ)> 0,则解不稳定,而σ=0则对应平面扭转DNA环的临界状态.将系数矩阵展开得到
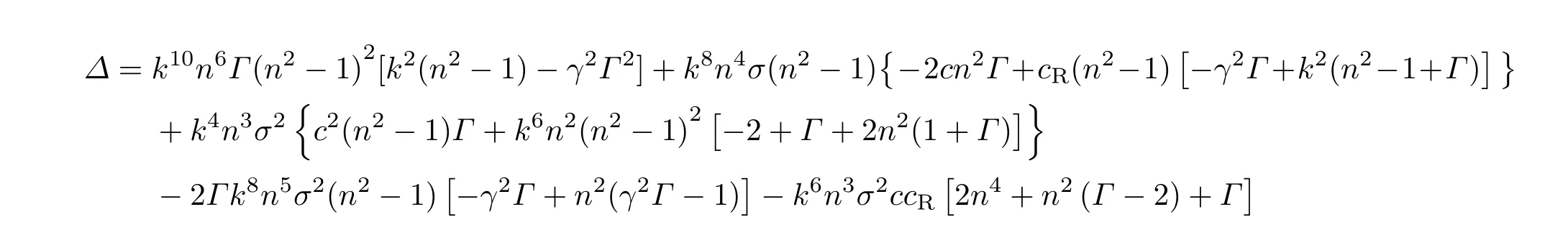
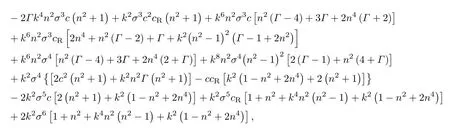
可以看由于存在黏性阻力和阻力矩,Δ中σ的次幂包含了0—6,而真空中[8]Δ中只包含σ的偶数次幂.
特征值σ=0对应平面扭转DNA环平衡的临界状态,我们得到扭转数
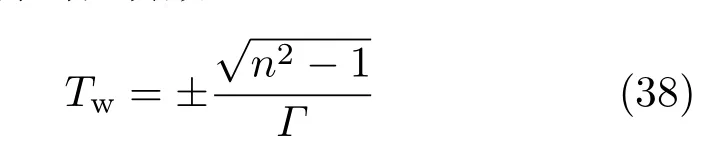
为平面扭转DNA环平衡稳定的临界判据.由临界判据(38)式,我们可得到对应于0和1两个模态时平面扭转DNA环是稳定的;对应于n=2的模态,我们得到扭转数的临界值为不稳定的模态取值范围为n≥2.与真空中结果[17,29]对比,我们发现DNA环平衡稳定性不受黏性阻尼影响.
对应Γ的典型比值范围[28],由临界判据(38)式我们可以得出为平面扭转DNA环的临界区域.
5.2不稳定性
若Re(σ)>0,则解是不稳定的.对应于扭率和曲率值γ=15,k=2,如令Γ=1,得出扭转数则此时平面扭转DNA处于不稳定态.黏性阻力系数取c=1,cR=4.给出σ2-n变化关系图,如图1所示.令c=cR=0,我们得到真空中σ2-n关系,见图2.对比可见黏性阻尼较小时,对于不稳定模态在2<n≤7范围内,黏性阻力的作用基本可以忽略.但是在n<2区域振幅出现分叉.黏性阻尼作用下平面扭转DNA环失稳后选择的模态为n=4.
增大黏性阻尼系数,例如取c=40,cR=160,σ与n的关系如图3所示,此时平面扭转DNA环失稳后选择的跳出平面的模态增大为n=7.说明黏性阻尼较大时,对平面扭转DNA环的不稳定影响较大.
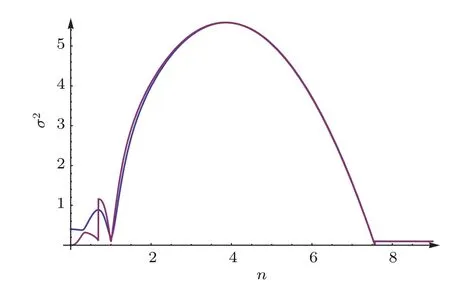
图1 (网刊彩色)σ2与n的关系,Tw=30,c=1,cR=4Fig.1.(color online)Relationship between of σ2and n,Tw=30,c=1,cR=4.

图2 (网刊彩色)σ2与n的关系,Tw=30,c=cR=0Fig.2.(color online)Relationship between of σ2and n,Tw=30,c=cR=0.
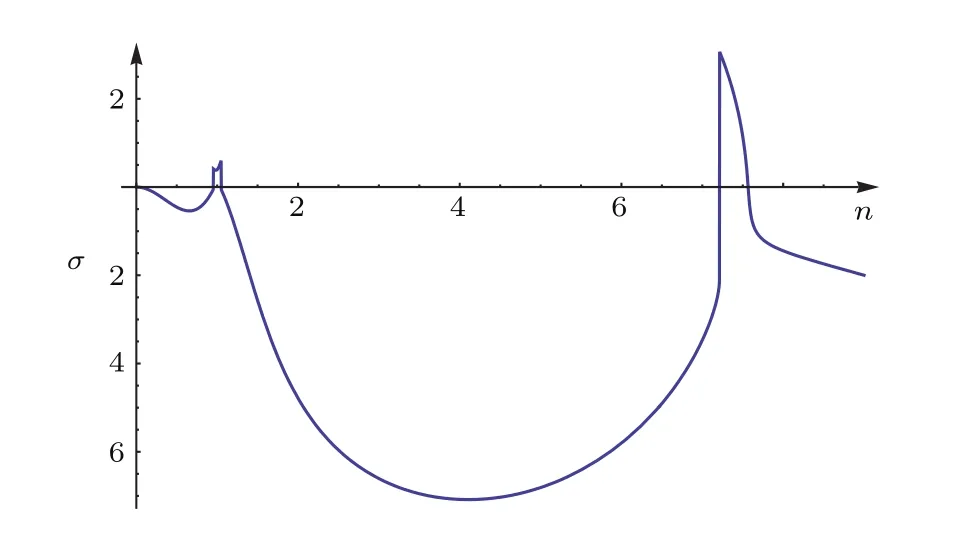
图3 σ与n的关系Tw=30,c=40,cR=160Fig.3.Relationship between of σ and n,Tw=30,c=40,cR=160.
6 总 结
本文基于坐标基矢的摄动,分析了黏性流体中超细长Kircho ff弹性杆动力学的稳定性,并应用于平面扭转DNA环.
1)得到黏性流体中超细长Kircho ff弹性杆动力学方程的一阶摄动表示,即方程(20)—(22)和(28)—(30)或者(31),该方程的解确定了黏性流体中超细长弹性杆的动力学稳定性判据和失稳后的模态选择.
2)给出了黏性流体中平面扭转DNA环的稳定性判据,得到平面扭转DNA环的稳定性典型临界值的区间.黏性阻尼项对超细长弹性杆的平衡稳定性无影响.
3)失稳状态下,黏性阻尼使得弹性环的振幅变小,并有分岔现象出现.黏性阻尼增大,DNA环失稳的模态数变大,并出现了多模态选择的动力学不稳定现象.并可预测不同黏性阻尼系数下优先选择的变形模态,从而可为控制其变形行为提供参考.
我们的研究目前还限于理论分析,尚未有实验验证.然而我们希望本文对模型的处理方法和得到的结果能够对以后的实验起到启发或者参考作用.
文献[9]指出在雷诺数为零时惯性项可忽略,此情形下超细长弹性杆的动力学行为尚待研究.在以后的工作中我们将考虑雷诺数为零的情况是否可以忽略惯性项?考虑流固耦合作用、生长等因素对黏性流体中超细长弹性杆动力学稳定性的影响.
[1]Beham C J 1977Proc.Natl.Acad.Sci.USA74 2397
[2]Le Bret M 1978Biopolymers17 1939
[3]Travers A A,Thompson J M T 2004Phil.Trans.R.Soc.Lond.A362 1265
[4]Benham C J,Mielke S P 2005Annu.Rev.Biomed.Eng.7 21
[5]Shi Y M,Hearst J E 1994J.Chem.Phys.101 5186
[6]Zhou H J,Ouyang Z C 1999J.Chem.Phys.110 1247
[7]Xue Y,Liu Y Z,Chen L Q 2004Chin.Phys.13 794
[8]Wang P,Xue Y 2016Nonlinear Dyn.83 1815
[9]Liu Y Z 2006Nonlinear Mechanics of Thin Elastic Rod-Theoretical Basis of Mechanical Model of DNA(Beijing:Tsinghua Press&Springer)p85(in Chinese)[刘延柱2006弹性细杆非线性力学-DNA力学模型的理论基础(北京:清华大学出版社&Springer)第85页]
[10]Bustamante C,Bryant Z 2003Nature421 423
[11]Tobias I,Swigon D,Coleman B D 2000Phys.Rev.E61 747
[12]Manning R S,Bluman G B 2005Proc.R.Soc.Lond.A461 2423
[13]Liu Y Z,Zu J W 2004Acta Mech.164 29
[14]Liu Y Z,Sheng L W 2007Acta Phys.Sin.56 2305(in Chinese)[刘延柱,盛立伟 2007物理学报 56 2305]
[15]Xue Y,Liu Y Z 2009Acta Phys.Sin.58 6737(in Chinese)[薛纭,刘延柱 2009物理学报 58 6737]
[16]Xue Y,Chen L Q,Liu Y Z 2004Acta Phys.Sin.53 4029(in Chinese)[薛纭,陈立群,刘延柱 2004物理学报53 4029]
[17]Goriely A,Tabor M 1997Physica D105 20
[18]Goriely A,Tabor M 1996Phys.Rev.Lett.77 3537
[19]Moulton D E,Lessinnes T,Goriely A 2013J.Mech.Phys.Solids61 398
[20]Klapper I 1996J.Comput.Phys.125 325
[21]Goldstein R E,Powers T R,Wiggins C H 1998Phys.Rev.Lett.80 5232
[22]Wolgemuth C W,Powers T R,Goldstein R E 2000Phys.Rev.Lett.84 1623
[23]Liu Y Z,Sheng L W 2007Chin.Phys.16 0891
[24]Keller J B,Rubinow S I 1976J.Fluid Mech.75 705
[25]Manning R S,Maddocks J H,Kahn J D 1996J.Chem.Phys.105 5626
[26]Kehrbaum S 1997Ph.D.Dissertation(Maryland:University of Maryland,College Park,USA)
[27]Hagerman P 1988Rev.Biophys.Chem.17 265
[28]Schlick T 1995Curr.Opinion Struct.Biol.5 245
[29]Zajac E E 1962Trans.ASME.J.Appl.Mech.29 136
PACS:45.10.Hj,45.40.–fDOI:10.7498/aps.66.094501
Dynamic instability of super-long elastic rod in viscous fl uid∗
Wang Peng1)†Xue Yun2)Lou Zhi-Mei3)
1)(School of Civil Engineering and Architecture,University of Jinan,Jinan 250022,China)2)(School of Mechanical Engineering,Shanghai Institute of Technology,Shanghai 201418,China)3)(Department of Physics,Shaoxing University,Shaoxing 312000,China)
14 November 2016;revised manuscript
18 December 2016)
The external environment a ff ects the structural form of biological system.Many biological systems are surrounded by cell solutions,such as DNA and bacteria.The solution will o ff er a viscous resistance as the biological system moves in the viscous fl uid.How does the viscous resistance a ff ect the stability of biological system and what mode will be selected after instability?In this paper,we establish a super-long elastic rod model which contains the viscous resistance to model this phenomenon.The stability and instability of the super-long elastic rod in the viscous fl uid are studied.The dynamic equations of motion of the super-long elastic rod in viscous fl uid are given based on the Kirchho ffdynamic analogy.Then a coordinate basis vector perturbation scheme is reviewed.According to the new perturbation method,we obtain the fi rst order perturbation representation of super-long elastic rod dynamic equation in the viscous fl uid,which is a group of the second order linear partial di ff erential equations.The stability of the super-long elastic rod can be determined by analyzing the solutions of the second order linear partial di ff erential equations.The results are applied to a twisted planar DNA ring.The stability criterion of the twisted planar DNA ring and its critical region are obtained.The results show that the viscous resistance has no e ff ect on the stability of super-long elastic rod dynamics,but a ff ects its instability.The mode selection and the in fl uence of the viscous resistance on the instability of DNA ring are discussed.The amplitude of the elastic loop becomes smaller under the in fl uence of the viscous resistance,and a bifurcation occurs.The mode number of instability of DNA loop becomes bigger with the increase of viscous resistance.
super-long elastic rod,perturbation method,viscous fl uid,instability
10.7498/aps.66.094501
∗国家自然科学基金(批准号:11262019,11372195,11472177)资助的课题.
†通信作者.E-mail:sdpengwang@163.com
*Project supported by the National Nature Science Foundation of China(Grant Nos.11262019,11372195,11472177).
†Corresponding author.E-mail:sdpengwang@163.com
