新型负模量声学超结构的低频宽带机理研究
2017-08-09张永燕吴九汇钟宏民
张永燕 吴九汇 钟宏民
1)(西安交通大学机械工程学院,机械结构强度与振动国家重点实验室,西安 710049)2)(四川理工学院机械工程学院,自贡 643000)
新型负模量声学超结构的低频宽带机理研究
张永燕1)2)吴九汇1)†钟宏民2)
1)(西安交通大学机械工程学院,机械结构强度与振动国家重点实验室,西安 710049)2)(四川理工学院机械工程学院,自贡 643000)
(2016年12月12日收到;2017年2月13日收到修改稿)
提出了一种具有负模量特性的新型声学超结构,并揭示了其低频带隙的形成及拓宽机理.通过理论推导给出了该新型结构的归一化有效模量表达式,由于有效模量的零值点与系统参数密切相关,可以调节合适的参数使得零值点降低或带隙下界降低,进一步实现低频带隙.理论结果表明,在一定的频率范围内,系统的弹性模量为负且负模量区域进一步拓宽,从而通过负模量区域的放大而拓宽带隙.这种新的实现低频带隙的方法克服了传统局域共振附加质量过大及惯性放大结构带隙较窄的缺点.同时,通过有限元法得到的周期结构的传输率随着结构参数的变化趋势与理论分析的变化趋势基本一致,并得到了约40—180 Hz的低频宽带.这种实现低频带隙的新思路对低频声波的控制具有很重要的理论指导意义.
负模量,声学超材料,低频宽带
1 引 言
在许多工程问题中,低频声波抑制一直是个难题.在这方面,已有很多研究工作[1−7],但是对低频声波的抑制仍然没有较好的方法.近年来,随着声子晶体和声学超材料的发展,很多学者在这方面进行了研究.最初从声子晶体Bragg散射机理来抑制声波传输,但是Bragg散射只能抑制高频,对低频声波的抑制没有较好的办法.后来,很多学者试图找到相应的左手声学超材料,即同时具有负质量密度和负弹性模量的材料.然而,并没有天然材料具有负质量密度或负模量特性.因此,一些学者采用人造微结构来实现负质量密度的表观效应[8−14]或者使用机械共振器“微结构”来形成声学超材料,并基于此提出了局域共振声子晶体的机理[15].为了控制低频声波,我们课题组基于局域共振声学超材料也做了不少工作,如张思文和吴九汇[16]提出了螺旋局域共振梁,但是对低频声波抑制效果仍然不理想.尽管对局域共振声学超材料的研究很多,并且声学超材料可以较好地控制声波传输,但是传统局域共振超材料仍存在一系列问题[17,18]:一方面,低频带隙较窄,为了拓宽低频带隙,一些学者通过对声学超材料结构进行梯度设计[19],在低频段实现了带隙拓宽;另一方面,传统局域共振结构往往存在附加质量过大的问题,针对这一问题,文献[20—22]提出了一种质量放大结构,并对其能带特性进行了分析,结果表明质量放大结构可以通过较小的附加质量实现低频带隙.总之,上述研究在某种程度上对实现低频带隙有一定的效果,但是利用梯度法拓宽低频带隙往往结构较大.同时,质量放大结构尽管可以实现共振频率降低,但低频带隙非常窄.如何很好地实现并进一步拓宽低频带隙,这个问题在以往的研究中并没能够很好地解决,仍然是个难题,也是迫切需要解决的问题.故探讨新的实现低频宽带的方法以及新的声学超材料结构是非常必要的.
因此,基于实现低频宽带这一难题,本文借鉴惯性放大结构提出了一种新型声学超材料结构,通过结构参数的设计使该系统在一定的频率范围内弹性模量为负,且负模量区域随着控制参数的变化而被拓宽,带隙的起始位置随着降低,这种实现、拓宽低频带隙的方法克服了通过惯性放大或者传统方法增加附加质量来降低共振频率的不足之处.与此同时,本文对低频带隙的形成及拓宽机理进行了深入分析.研究内容安排如下:第2部分探讨具有负模量特性的新型声学超结构及宽带机理;第3部分是数值仿真及讨论;第4部分是结论.
2 具有负模量特性的新型声学超结构及宽带隙机理
2.1新型结构单元负模量特性及宽带机理分析
为了更好地解决实现低频宽带这一难题,借鉴质量放大结构[20−22],本文提出了如图1所示的新型声学超材料结构,三角形三边视为无质量弹簧,三个端点为集中质量.其中,水平方向两端点质量设为m,垂直方向上点质量设为m2,水平边弹簧刚度为k.这里假设斜边弹簧为刚性,当两个水平质点m产生相向位移u时,本文只考虑位移很小的情况.

图1 具有负模量特性的新型结构单元Fig.1.A new type of structural element with negative modulus.
根据x方向上由谐振力F作用引起的应力-应变关系,则系统在x方向上的运动方程为
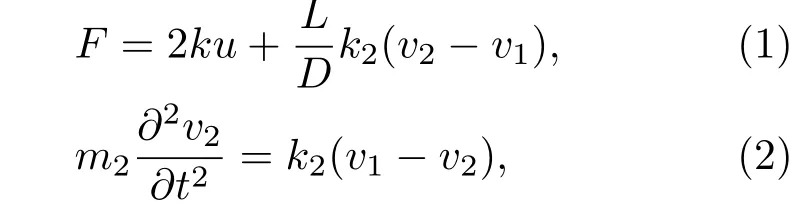
在上述方程中,考虑谐波激振力F=Aeiωt,其中A谐波激振力的振幅,ω是激振频率.假设位移很小时,则有


如图1所示的横截面积为A的一维连续弹性固体,则应力应变关系定义为


从方程(6)可以看出,该系统的归一化有效模量与该系统的结构参数密切相关:1)当驱动频率等于局部谐振频率时,即η=1时,有效模量的值达到无穷大,且是无界的,即当时,有效模量的值接近无穷大;2)当有效模量的值等于零,这时其对应频率
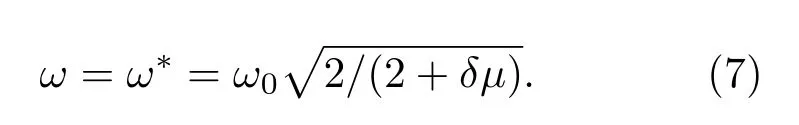
由此可见,对于η<1时,在ω0和ω∗之间的任意一个频率值对应的有效模量值都为负.众所周知,负模量区域即对应带隙的频率范围,那么带隙的频率范围即在ω0和ω∗之间.也就是说,等效模量零值点与系统共振点(Eeff/E0→ ∞或者ω/ω0=1)之间的距离即为带隙的宽度,且等效模量的零值点为带隙起始点,即带隙下界频率起始点为ω∗.从方程(7)我们可以看到带隙下界的起始点ω∗与这个新型声学超结构的刚度比δ成正比关系,与结构参数D(µ=L/D)成反比关系.为了达到低频效果,我们可以调节这两个参数使得等效模量的零值点降低即带隙下界降低,这样等效模量的零值点与共振点之间的距离也增大了,进而实现并拓宽了低频带隙.
根据我们得出的结论:1)负模量区域即对应带隙的频率范围,即在ω0和ω∗之间;2)等效模量的零值点与共振点(ω/ω0=1或Eeff/E0→ ∞)之间的距离即为带隙的宽度;3)等效模量的零点值ω∗即带隙起始点,其与刚度比δ成正比关系,而与结构参数D(µ=L/D)成反比关系.图2和图3描述了方程(6)所示的新型结构单元的负模量区域随着这两个控制参数的变化趋势.如图2所示,当D=6 mm时,带隙起始点ω∗约为0.8,负模量区域对应的无纲量频率范围为0.8—1;当D=15 mm时,带隙起始点ω∗约为0.6,负模量区域对应的无纲量频率范围约为0.6—1.显然,随着参数D从6 mm增加到15 mm时,负模量零值点由0.8降到了0.6,即带隙的下界降低了,系统的负模量区域被放大了两倍多.也就是说系统的有效模量零值点(ω∗)与共振点(ω/ω0=1)之间的距离被放大了两倍多,即带隙被拓宽了两倍多.与此同时,如图3所示,当刚度比δ=0.8时,带隙起始点ω∗约为0.6,负模量区域为0.6—1;当δ=3时,带隙起始点ω∗约为0.85,负模量区域为0.85—1.很显然,在图2和图3中,随着控制参数的变化,带隙的下界都降低了,负模量区域都被拓宽了,即系统有效模量的零值点(ω∗)与共振点(ω/ω0=1)之间的距离都增大了,也就是低频带隙被拓宽了.
因此,这种新的拓宽低频带隙的方法,即通过系统结构参数的设计实现该系统的负模量区域放大及带隙起始位置的降低,从而实现和拓宽低频带隙,其克服了传统梯度法[17]扩大带隙及惯性放大结构[18−20]等实现低频带隙的不足之处.

图2 (网刊彩色)当刚度比δ=1时,负模量区域随控制参数D的变化Fig.2.(color online)The variation of the region of negative modulus with the control parameter D for the sti ff ness ratio δ of 1.
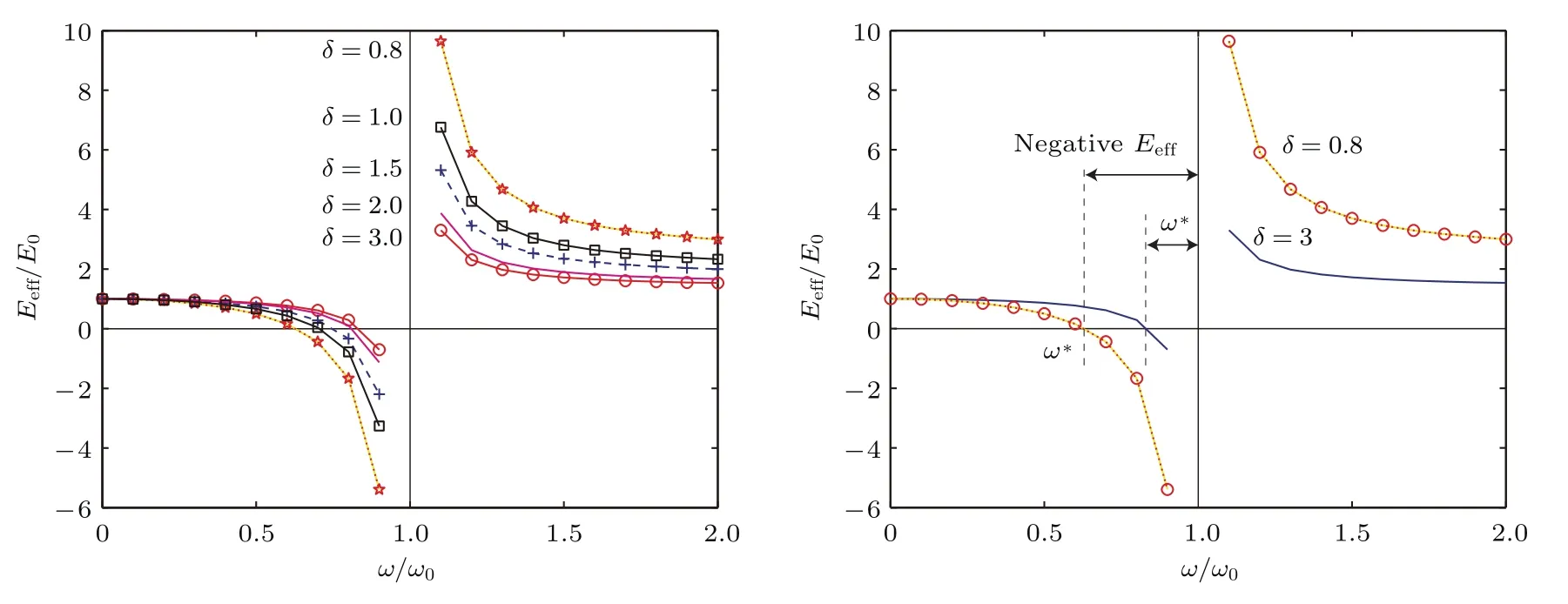
图3 (网刊彩色)当D=12 mm时,负模量区域随系统刚度比的变化Fig.3.(color online)The variation of the region of negative modulus with the sti ff ness ratio δ for the control parameter D of 12 mm.
2.2新型超材料周期结构的色散关系分析
基于上述分析得出的理论思想:系统共振点(Eeff/E0→∞)与系统等效模量零值点(Eeff/E0=0)之间的距离为带隙的宽度,且等效模量的零值点(Eeff/E0=0)为带隙的起始位置,其与系统刚度比δ成正比关系,而与结构参D成反比关系.针对如图1所示的新型单元结构,构建新型声学超材料周期结构如图4所示.该一维模型中的基体由m1表示,则第j个单元的运动方程

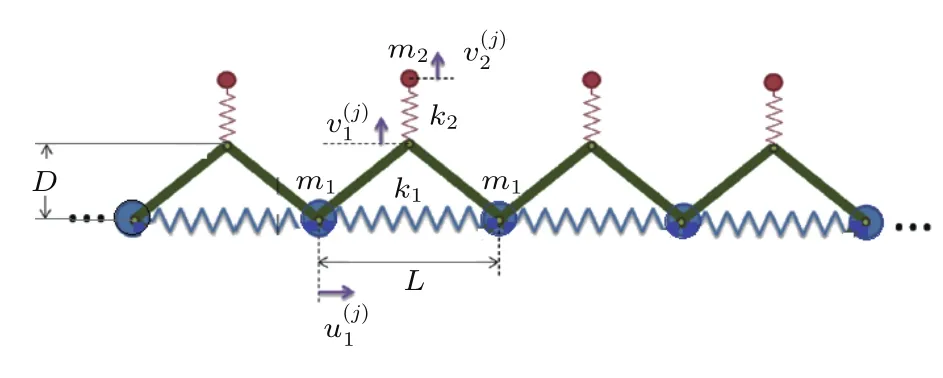
图4 新型结构单元的周期结构Fig.4.Periodic structure of new-type structure unit.
将谐波运动方程代入方程(8)和(9)中,可得该周期结构的色散方程如下:

其中,θ=m2/m1为质量比,ξ=qL为无量纲波数.
图5描述了方程(10)的色散曲线.从图5(a)可以清晰地看到,D=20 mm时的带隙下界较D=8 mm的带隙下界下降了很多,这与我们2.1节得出的结论(带隙下界位置与参数D成反比关系)相符合,同时带宽被拓宽了两倍多.与此同时,从图5(b)可以很清楚地看到刚度比为1时的带隙下界较刚度比为3时的带隙下界也降低了,并且带宽也被拓宽了两倍多.总之,随着控制参数的变化,带隙下界都降低了,低频带隙都被拓宽了,这与上述分析结果一致.

图5 由方程(10)得到的新型周期结构的色散关系(a)色散关系随着参数D的变化;(b)色散关系随着刚度比δ的变化Fig.5.The dispersion relation of the novel periodic structure obtained by Eq.(10):(a)The variation of the dispersion relation with the parameter D;(b)the variation of the dispersion relation with the sti ff ness ratio with δ.
3 数值仿真与讨论
我们设计了如图6所示的具有负杨氏模量的声学超材料,该设计采用嵌入如图1所示的微结构的主体材料形式,弹簧k1在此表示基体材料的刚度.定义x及y方向上均为周期性边界,选取如表1所列的数据,利用有限元法得到了如图7所示的无限周期结构的色散曲线.很显然,数值仿真结果和理论结果基本符合.
为了进一步分析声波在有限周期结构中的传输率,我们构建了如图8所示的具有负杨氏模量的有限周期声学超材料,针对x方向上5个新型单元超材料周期结构,在左端施加x方向谐波激励力,x方向的位移分别在点A和B处测量.选取如表1所列的数据,并用COMSOL 4.3b对5个新型超材料周期结构的透射率进行了计算.如图9所示,当D=8 mm时,声波在0—20 Hz的频率范围内基本都形成了透射峰A,只有在约40—100 Hz频率及100—180 Hz段各形成一条带隙;当D=20 mm时,很显然,低频的透射峰A下降变为带隙,形成了20—200 Hz整个频段的宽带隙,这说明带隙随着参数D的增大,带隙边界逐渐下降且被拓宽了.同时,图10描述了这个新型超材料有限周期结构的透射率随着系统刚度比的变化趋势.随着系统刚度比的减小,在约90—140 Hz频段内的透射峰都大幅度下降而形成带隙,并在40 Hz以下及40—200 Hz的频率范围内产生了低频带隙.很显然,通过有限元方法计算的周期结构的透射率变化趋势和第2部分的理论分析结果高度符合,即带隙的宽度随着刚度比的减小或者随着系统参数D的增大而被拓宽.

表1 材料参数Table 1.The parameters of materials.
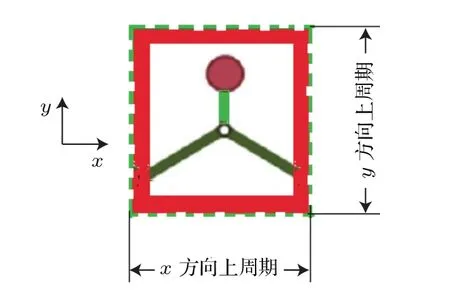
图6 具有负杨氏模量的新型超材料无限周期结构Fig.6.In fi nite periodic structure of novel metamaterials with negative modulus.

图7 理论结果和有限元结果的比较Fig.7.Comparison of theoretical results and fi nite element results.
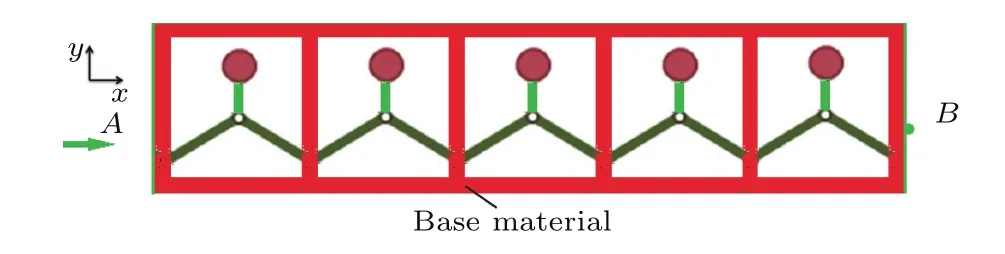
图8 具有负杨氏模量的新型超材料有限周期结构Fig.8.Finite periodic structure of novel metamaterial with negative modulus.

图9 (网刊彩色)5个周期结构的透射率,其中,实心圆点线段为D=8 mm,空心圆点线段为D=20 mmFig.9.(color online)The transmittance of the fi ve periodic structures:the solid dotted line for D=8 mm and the hollow dotted line for D=20 mm.
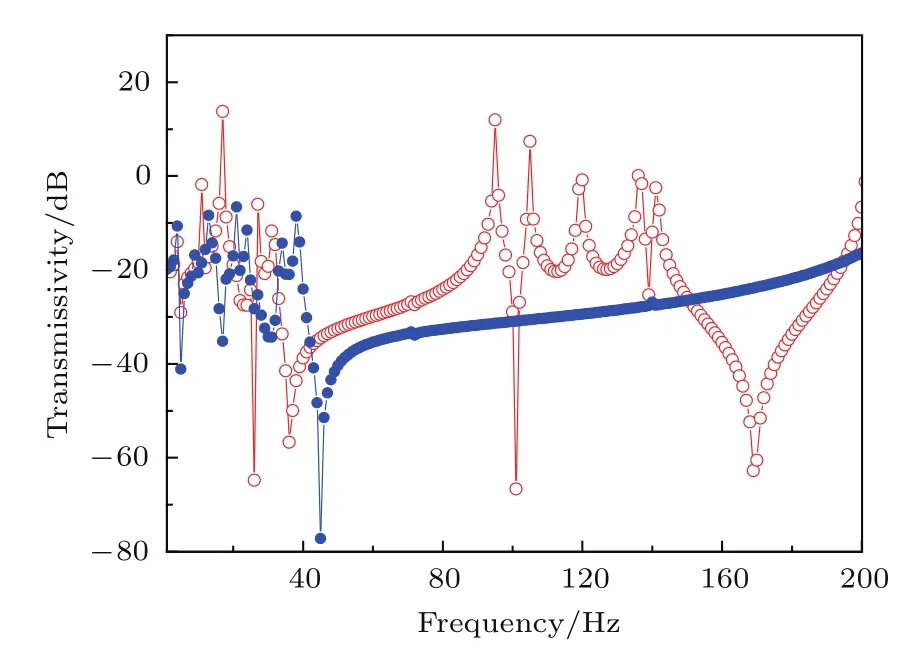
图10 (网刊彩色)5个周期结构的透射率,其中,空心圆点线段对应刚度比大于1,实心圆点线段对应刚度比为1 Fig.10.(color online)The transmittance of the fi ve periodic structures:the hollow dotted line for the sti ffness ratio greater than 1 and the solid dotted line for the sti ff ness ratio of 1.
4 结 论
本文对一类新型声学超结构进行了深入分析,该结构可以实现并拓宽低频带隙,并得出了一些新结论.
1)该结构的归一化有效模量与结构参数密切相关,通过设计结构参数可以使系统的弹性模量在一定的频率范围内为负且负模量区域与带隙的形成直接相关联:a)负模量区域即对应带隙的频率范围,即在ω0和ω∗之间;b)等效模量的零值点或Eeff/E0=0)与共振点(ω/ω0=1或Eeff/E0→ ∞)之间的距离即为带隙的宽度;c)等效模量的零点值ω∗即带隙起始点与刚度比δ成正比关系,而与D(µ=L/D)成反比关系.这样,我们只要调节合适的参数使得负模量的零值点降低,便可以实现低频带隙的拓宽,达到低频效果.
2)数值仿真结果表明,当D从8 mm增大到20 mm时,带隙被拓宽两倍且带隙下界降低了许多,产生了低频大宽带;当刚度比减小时,带隙同样被拓宽了,并且带隙下界下降了许多,实现了低频带隙.另外,通过有限元方法计算周期结构的传输率与理论分析结果高度符合,并在40 Hz以下的频率段形成了较低频带隙及在40—180 Hz频率范围内形成了低频大宽带.
这种实现低频宽带的机理为低频声波控制奠定了一定的理论基础,且所提出的新型声学超材料结构,为获得低频、超低频带隙提供了一种有效的方法,在低频减振降噪方面有潜在的应用前景.
[1]Pai P F,Peng H,Jiang S 2014Int.J.Mech.Sci.79 195
[2]Gusev V E,Wright O B 2014New J.Phys.16 123053
[3]Gao J,Cheng J C,Li B W 2007Appl.Phys.Lett.90 111908
[4]Wang Y F,Wang Y S,Wang L T 2014J.Phys.D:Appl.Phys.47 015502
[5]Chronopoulos D,Antoniadis I,Collet M,Ichchou M 2015Wave Motion58 165
[6]Zhu R,Liu X N,Hu G K,Sun C T,Huang G L 2014J.Sound Vib.333 2759
[7]Nouh M,Aldraihem O,Baz A 2015J.Sound Vib.341 53
[8]Huang H H,Sun C T,Huang G L 2009Int.J.Eng.Sci.47 610
[9]Jaglinski T,Kochmann D,Stone D,Lakes R S 2007Science315 620
[10]Lakes R S,Lee T,Bersie A,Wang Y C 2001Nature410 565
[11]Lee S H,Park C M,Seo Y M,Wang Z G,Kim C K 2009Phys.Lett.A373 4464
[12]Lee S H,Park C M,Seo Y M,Wang Z G,Kim C K 2009J.Phys.:Conden.Matter21 175704
[13]Cheng Y,Zhou C,Yuan B G,Wu D J,Wei Q,Liu X J 2015Nat.Mater.14 1013
[14]Cheng Y,Xu J Y,Liu X J 2008Appl.Phys.Lett.92 051913
[15]Liu Z,Zhang X,Mao Y,Zhu Y Y,Yang Z,Chan C T,Sheng P 2000Science289 1734
[16]Zhang S W,Wu J H 2013Acta Phys.Sin.62 134302(in Chinese)[张思文,吴九汇 2013物理学报 62 134302]
[17]Liu M,Hou Z L,Fu X J 2012Acta Phys.Sin.61 104302(in Chinese)[刘敏,侯志林,傅秀军 2012物理学报 61 104302]
[18]Wu J,Bai X C,Xiao Y,Geng M X,Yu D L,Wen J H 2016Acta Phys.Sin.65 064602(in Chinese)[吴健, 白晓春,肖勇,耿明昕,郁殿龙,温激鸿 2016物理学报 65 064602]
[19]Baravellie,Ruzzene M 2013J.Sound Vib.332 6562
[20]Zhang Y,Yin J F,Wen J H,Yu D L 2016J.Vib.Shock35 27(in Chinese)[张印,尹剑飞,温激鸿,郁殿龙2016振动与冲击35 27]
[21]Yilmaz C,Hulbert G M,Kikuchi N 2007Phys.Rev.B76 054309
[22]Yilmaz C,Hulbert G M 2010Phys.Lett.A374 3576
PACS:43.20.+g,43.40.+s,62.25.JkDOI:10.7498/aps.66.094301
Low-frequency wide-band mechanism of a new type acoustic metamaterial with negative modulus
Zhang Yong-Yan1)2)Wu Jiu-Hui1)†Zhong Hong-Min2)
1)(School of Mechanical Engineering and State Key Laboratory for Strength and Vibration of Mechanical Structures,Xi’an Jiaotong University,Xi’an 710049,China)2)(School of Mechanical Engineering,Sichuan University of Science and Engineering,Zigong 643000,China)
12 December 2016;revised manuscript
13 February 2017)
In this paper,a new type of acoustic metamaterial with negative modulus is proposed,and the formation and broadening mechanism of the low frequency bandgap are revealed.The expression of the normalized e ff ective modulus of the structure is derived theoretically.Since the zero value of the e ff ective modulus is closely related to the system parameters,the appropriate parameters can be adjusted to reduce the zero point,and the lower bound of the bandgap is reduced,thus the low-frequency bandgap is realized.The theoretical results show that the elastic modulus of the system is negative and the region of the negative modulus is widened in a certain frequency range,therefore,the widening of the bandgap can be realized through the enlargement of the negative modulus region.This new mechanism for achieving low-frequency bandgap overcomes the shortcomings both in the traditional local resonance with too large additional mass,and in the inertial ampli fi cation structures with narrow bandgaps.At the same time,the transmission of this periodic structure obtained by the fi nite element method is highly consistent with that by the theoretical analysis,with a low-frequency band of 40–180 Hz,from which the new mechanism presented here is veri fi ed.This new idea of achieving low-frequency bandgap is of great theoretical signi fi cance for controlling low-frequency sound waves.
negative modulus,acoustic metamaterial,low-frequency broadband
10.7498/aps.66.094301
†通信作者.E-mail:ejhwu@mail.xjtu.edu.cn
†Corresponding author.E-mail:ejhwu@mail.xjtu.edu.cn
