一种滑移区气体流动的格子Boltzmann曲边界处理新格式∗

顾娟 黄荣宗 刘振宇 吴慧英

(上海交通大学机械与动力工程学院,上海 200240)

一种滑移区气体流动的格子Boltzmann曲边界处理新格式∗

顾娟 黄荣宗 刘振宇 吴慧英†

(上海交通大学机械与动力工程学院,上海 200240)

(2016年12月18日收到;2017年4月5日收到修改稿)

针对滑移区复杂气-固边界存在速度滑移现象,提出了一种基于格子Boltzmann方法的非平衡态外推与有限差分相结合的曲边界处理新格式.该格式具有可考虑实际物理边界与网格线偏移量的优势,较传统half-way DBB(di ff usive bounce-back)格式更能准确反映实际边界情况,同时还可获取壁面处气体宏观量及其法向梯度等信息.采用本文所提曲边界处理格式模拟分析了滑移区气体平直/倾斜微通道Poiseuille流、微圆柱绕流和同心微圆柱面旋转Couette流问题.研究结果表明,采用曲边界处理新格式所得结果与理论值以及文献结果符合良好,适用于滑移区气体流动的复杂边界处理,且比half-way DBB格式具有更高的精度,较修正DBB格式具有更好的适应性.

曲边界,格子Boltzmann方法,滑移区,微气体流动

1 引言

随着微机电系统(micro-electro-mechanical system,MEMS)技术在生物医疗、信息通讯及国防军工等诸多领域的逐步应用,微尺度条件下新的物理现象引起了越来越多学者的重视[1,2].其中对于微尺度气体流动[3,4]问题,因气体分子平均自由程λ与特征尺寸H两者数量级相当,气体稀薄效应已不可忽略.气体稀薄程度可用Knudsen数表示,Knudsen数(Kn)的定义为Kn=λ/H.滑移区(0.001 6 Kn 6 0.1)气体在气-固边界处将出现明显的速度滑移现象,基于连续介质假定的Navier-Stokes方程需结合滑移边界条件方可描述该问题.有别于传统计算流体动力学方法,格子Boltzmann(LB)方法不受连续介质假定限制,具有微观粒子特性和介观物理背景,成为研究微尺度气体流动问题的理想数值方法[5−7].

目前,针对常规尺度曲边界处理的研究已有较多文献报道[8−22],其中非平衡外推格式[8]已被证明可有效处理复杂曲边界问题[13,20],前人也对Ladd[10]提出的考虑边界速度的half-way反弹格式进行了修正以推广到曲面边界条件.Yin和Zhang[15]基于Ladd[10]的half-way反弹格式将虚拟节点(实际物理边界附近流体格点与固体格点连线的中点)处速度取代原格式中的壁面速度,提高了模拟复杂边界问题的精度.在此基础上,史冬岩等[16]对离流体格点较近的虚拟节点速度进行修正,进一步提高了计算精度.尽管以上方法在常规尺度曲边界处理中表现出较好的优越性,但由于其不能反映因微尺度气体-壁面相互作用引起的边界速度滑移,无法适用于微尺度滑移区流动问题中复杂曲边界的处理.Szalmas[23]采用贴体曲坐标下SRB(specular-re fl ection-bounceback)格式有效地模拟了微尺度复杂气-固边界速度滑移问题,但贴体网格需要求解Jacobi变换矩阵,增加了编程复杂度.另一类处理曲边界的方法是采用笛卡尔网格系统,不需要进行网格变换,方便处理各种复杂物理边界,但问题在于网格边界与物理边界不重合,因此边界条件的处理尤为重要[24].针对这个问题,Guo等[25]采用half-way DBB格式处理同心微圆柱面旋转Couette流,但该方法仅当虚拟节点与固体壁面重合时,才能体现其计算精度优势.Suga[26]将插值格式分别引入到BB(bounce-back)格式和DS(di ff usescattering)格式中组合为IDBB(interpolation di ff usive bounce-back)格式以处理微尺度流动问题,但其组合系数的选取仍参考传统half-way DBB格式.Tao和Guo[24]在DBB格式中引入实际物理边界与网格线偏移量这一参数,并应用其对模型松弛时间τq和参数r进行修正,将适用于平直边界的DBB格式推广至滑移曲边界情况.当偏移量为半个格子时,该格式则还原为half-way DBB格式,但为保证参数τq和r取值的合理性,增加了滑移边界条件中气体-壁面相互作用参数取值的难度.Yang等[27]提出一种考虑速度滑移的浸入边界格子Boltzmann方法,并用其模拟微气体挤压膜阻尼效应引起的空腔内刚性物体振动,但仅验证了该方法在不考虑稀薄效应情况下的准确度.目前针对滑移区曲边界的速度滑移问题,精度高、适用性广的方法鲜有研究报道.

本文提出了一种综合Guo等[8]非平衡态外推及Le等[17]有限差分格式的曲边界处理格式,该格式考虑了实际物理边界与网格线的偏移量,较halfway DBB格式更能准确地描述实际物理边界的情况.由于不涉及参数取值合理性问题,本文所提格式较修正DBB格式更能适应气体-壁面相互作用参数的选取,同时还可获得壁面处气体宏观量及其法向梯度等信息.基于本文所提格式对滑移区气体平直/倾斜微通道Poiseuille流、微圆柱绕流和同心微圆柱面旋转Couette流问题进行LB数值模拟研究,将模拟结果与解析解及已有文献结果进行对比讨论,以分析本文所提格式的准确度与适用性.

2 LB模型与曲边界格式

2.1 微流动的LB基本模型

LB模型通过格点上微观粒子分布函数的演化过程来描述流体的流动.本文采用单松弛(LBGK)模型[28],其演化方程为

其中,ci为粒子在i方向的速度,δt为时间步长,fi(x,t)为t时刻x位置处以速度ci运动的粒子的分布函数,τ为无量纲松弛时间.(x,t)为i方向粒子的平衡态分布函数,

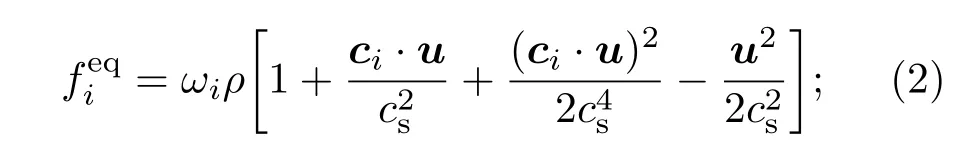
Fi(x,t)为离散外力项[29]

式中,ωi为权系数,cs为格子声速,G为外力.宏观物理量密度ρ和速度u的计算式为

对于二维问题,本文选用二维九速(D2Q9)模型,相应的离散速度为

其中,粒子迁移速率c=δx/δt(δx为格子步长),格子声速权系数ω0=4/9,ω1=ω2=ω3=ω4=1/9,ω5=ω6=ω7=ω8=1/36.通过Chapman-Enskog分析可知,模型对应的流体压力P=,流体的运动黏度ν=(τ−0.5)δt.

对于微尺度气体流动问题,需在模型中引入Knudsen数的影响.由动理学理论可知,气体分子平均自由程λ与动力黏度µ、压力P、温度T的关系式为结合Knudsen数的定义式Kn=λ/H及LB模型中运动黏度ν与无量纲松弛时间τ的关系式ν=c2s(τ−0.5)δt,可得模型中无量纲松弛时间与Knudsen数的关系式为

2.2微尺度流动的曲边界处理

对于微尺度气体流动问题,壁面处滑移边界条件的处理至关重要.本文在Guo等[8]的非平衡态外推格式的基础上,提出了一种复杂曲边界上壁面滑移速度的边界处理格式.如图1所示的曲边界,xf为流体格点,xs为固体内部格点,xint为固体边界格点.流体格点xf处i方向的未知分布函数fi(xf,t+δt)由固体格点xs处的分布函数fi(xs,t)演化得到,而fi(xs,t)采用Guo等[8]的非平衡态外推格式重构得到.为此,首先将固体格点处的分布函数分解为平衡态和非平衡态两部分,即

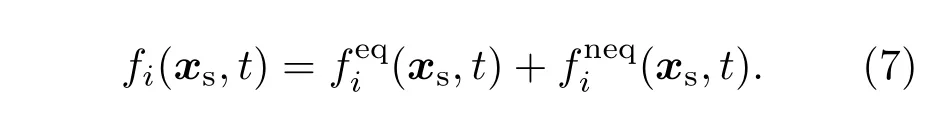
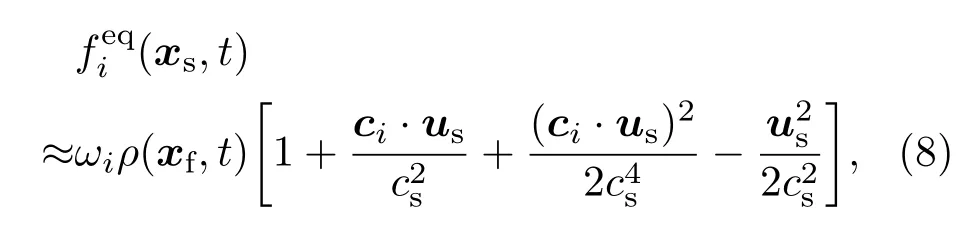
式中us可由u(xint),u(xf)及u(xff)外推确定

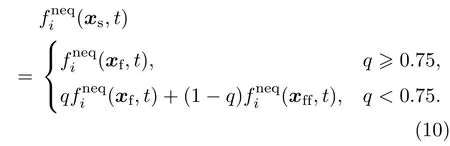
需要指出的是,对于微尺度气体流动问题,壁面处气体速度ug(即u(xint))不等于固体壁面速度uw,需进一步考虑滑移速度uslip的影响.本文采用微尺度一阶滑移曲边界条件[30],

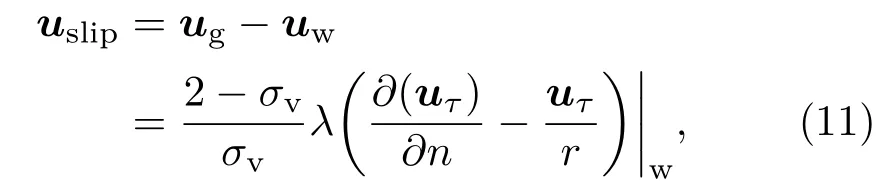
其中,uτ为气体在壁面处的切向速度矢量,r为半径,σv为动量协调系数.对于平直边界(r→∞)也适用,此时(11)式括号内第二项为0,与微尺度经典的Maxwell-Smoluchowski一阶滑移直边界条件[1]表达式一致.对于完全漫反射固体壁面,有σv=1[3−7,23−27].针对复杂曲边界,本文采用Le等[17]提出求解壁面法向温度梯度的有限差分格式求解壁面处流体速度的法向梯度.如图1所示,沿壁面法向n在流体内部选取两个虚拟点x′和x′′,满足|x′′−x′|=|x′−xint|=δ.为保证紧邻x′(x′′)的四个网格点均为流体格点,本文取δ=1.5δx.对于虚拟点x′处的流体宏观速度,通过其紧邻的流体网格点采用双线性插值法确定,即有

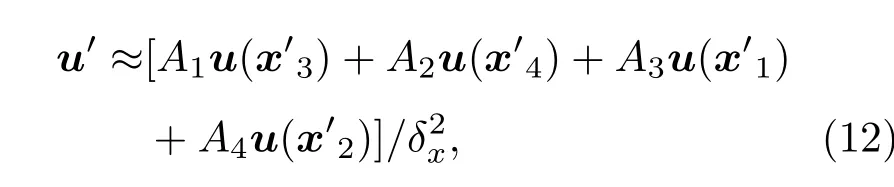
其中A1,A2,A3和A4分别为x′所在网格内四块子区域的面积(如图1所示).采用相同方法可求得虚拟点x′′处的流体宏观速度u′′.由虚拟点x′和x′′处的流体宏观速度,结合(11)式,可求得壁面处气体速度为

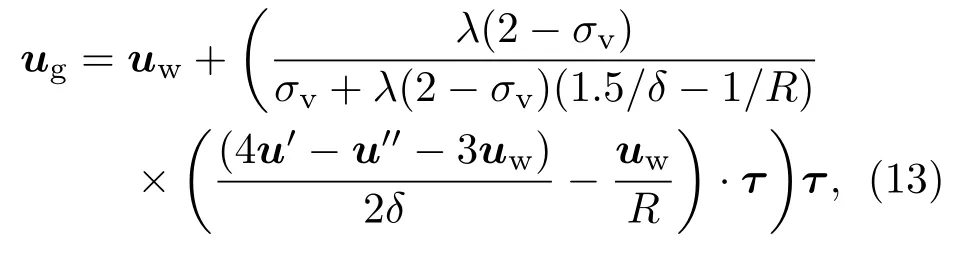
其中第二项即为微尺度壁面处气体滑移速度,R为固壁的曲率半径.

图1 曲边界示意图Fig.1.Schematic illustration of the curved boundary.

3 结果与讨论

为验证本文提出的滑移区曲边界滑移速度边界处理格式的适用性,本节依次模拟研究平直/倾斜微通道Poiseuille流、微圆柱绕流和同心微圆柱面旋转Couette流问题.

3.1 平直微通道Poiseuille流

微尺度Poiseuille流在MEMS中广泛存在且有解析解,可用于验证滑移边界处理方法的准确度.本文模拟了网格线与平直微通道壁面偏移量qδx(q=0.25,0.5,0.75,1.0)不同情况下的滑移区外力驱动Poiseuille流.微通道内气体受到沿流动方向恒定外力Gx=10−4的驱动,进出口采用周期性边界条件,固体边界上的滑移速度边界条件((11)式)采用本文提出的边界处理格式处理.计算过程中,计算网格取为Nx×Ny=4×32.对于该微尺度Poiseuille流,沿截面方向速度分布的解析解为

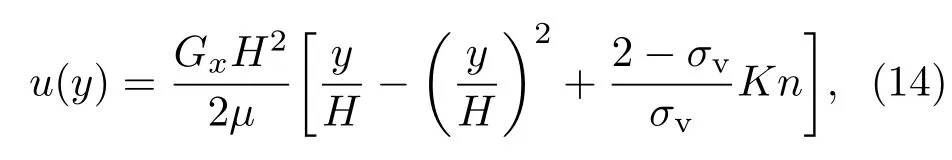
其中H为微通道的宽度.

图2(a)和图2(b)分别给出了当Kn=0.0194时,采用本文格式和half-way DBB格式计算得到的截面无量纲速度分布与解析解的对比情况.由图2可知,本文格式得到的截面无量纲速度分布和解析解在不同q情况下均符合良好;而half-way DBB格式得到的结果仅在q=0.5时才与解析解一致,这是因为half-way DBB格式基于half-way反弹格式,当偏移量为0.5δx时,half-way DBB格式中的虚拟边界与实际物理边界重合,固体边界可由虚拟边界准确刻画,故此时计算精度最高.但当偏移量发生改变时,half-way DBB格式因默认偏移量为0.5δx,故其模拟结果并未有相应改变,仍对应q=0.5条件下的计算结果.故对于偏移量不为0.5δx,half-way DBB格式已不能再准确描述固体边界的实际情况.

为定量比较本文格式与half-way DBB格式的计算优势,定义了如下误差量:1)最大相对误差,

2)相对误差,

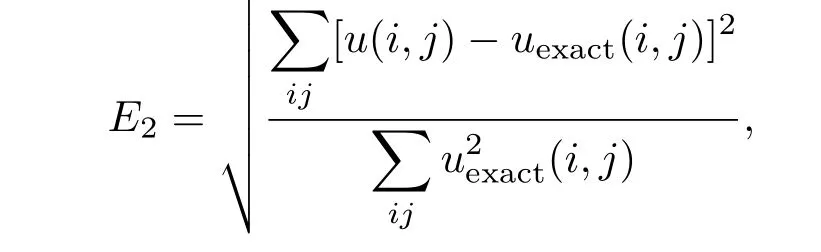
其中,(i,j)为计算域上的网格点,u(i,j)为流体格点上的速度值,uexact(i,j)为流体格点上的速度的解析值.表1给出了不同q条件下(Kn=0.0194),本文格式与half-way DBB格式计算结果误差对比情况.从表中可知,如前所述half-way DBB格式仅在q=0.5时误差才达最小值,本文格式在其余不同偏移量条件下较half-way DBB格式计算精度都有明显提高.

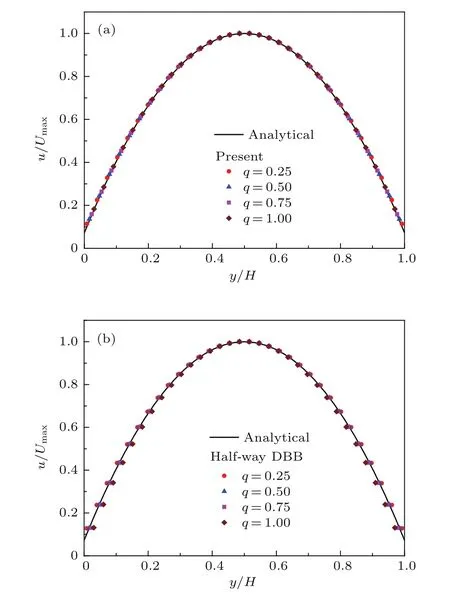
图2 (网刊彩色)不同q时平直微通道截面无量纲速度分布(Kn=0.0194)(a)本文格式模拟结果;(b)half-way DBB格式模拟结果Fig.2.(color online)Normalized velocity pro fi les of the aligned microchannel fl ow with di ff erent values of q(Kn=0.0194):(a)The present scheme;(b)the half-way DBB scheme.

3.2 倾斜微通道Poiseuille流

为进一步验证本文提出的格式能有效处理滑移区复杂的几何边界,对图3所示的倾斜微通道内外力驱动Poiseuille流进行了模拟.微通道倾斜角度θ依次取为arctan(0.46),arctan(1.20)和arctan(3.72),计算网格取为Nx×NAB=100×100,对应的y方向格点数为Ny=NAB+Nxtanθ.对于该倾斜微通道Poiseuille流,截面速度分布解析解仍如(14)式所示,其中y代表到微通道下壁面的垂直距离,H为微通道的宽度.

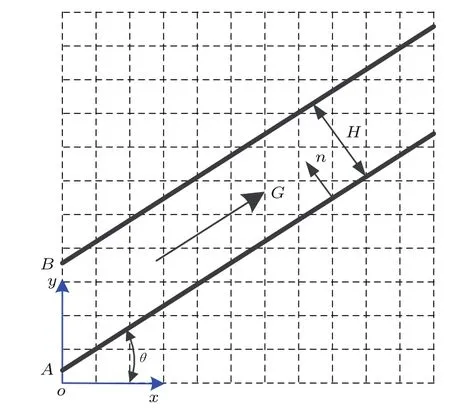
图3倾斜微通道示意图Fig.3.Schematic illustration of the inclined microchannel.

图4 (a)和图4(b)分别给出了当Kn=0.0194时,采用本文格式和half-way DBB格式计算得到的截面无量纲速度分布与解析解对比情况.由图4可知,在不同倾斜角度情况下,本文格式的模拟结果和解析解始终符合良好,而half-way DBB格式的模拟结果在微通道壁面处将显著偏离理论值.这是因为halfway DBB格式实际物理边界与网格线偏移量恒为0.5δx,使得倾斜的微通道壁面成为阶梯状.

表2给出了不同倾斜角条件下(Kn=0.0194),本文格式与half-way DBB格式计算结果误差对比情况.从表2可知,本文格式较half-way DBB格式在模拟不同倾斜角时最大相对误差及相对误差均明显降低.

图4 (网刊彩色)不同倾斜角θ时,倾斜微通道截面无量纲速度分布(Kn=0.0194)(a)本文格式模拟结果;(b)half-way DBB格式模拟结果Fig.4.(color online)Normalized velocity pro fi les of the inclined microchannel fl ow with di ff erent inclined angles θ(Kn=0.0194):(a)The present scheme;(b)the half-way DBB scheme.

表2 不同倾斜角条件下本文格式与half-way DBB格式计算误差对比(Kn=0.0194)Table 2.Computational errors of the present scheme and the half-way DBB scheme with di ff erent inclined angles θ(Kn=0.0194).

表1 不同q条件下本文格式与half-way DBB格式计算误差对比(Kn=0.0194)Table 1.Computational errors of the present scheme and the half-way DBB scheme with di ff erent values of q(Kn=0.0194).

3.3微圆柱气体绕流

圆柱绕流是流体力学中经典的复杂外流问题,常被用于检测曲边界的处理能力.本节对微圆柱气体绕流问题进行模拟,并将模拟结果与文献结果[31]进行对比验证.对于微圆柱绕流问题,Reynolds数的定义为

其中,U∞为均匀来流速度,D为微圆柱直径.在模拟过程中,计算区域选取为40D×20D(D划分为30个格子),微圆柱放置在离进口及上下边界均为10D的位置.计算区域边界条件设置如下:

图5 (网刊彩色)微圆柱绕流(Re=20,Kn=0.015)(a)微圆柱附近流线;(b)微圆柱表面无量纲滑移速度分布Fig.5.(color online)Flow past a microcylinder(Re=20,Kn=0.015):(a)Streamlines around the microcylinder;(b)normalized slip velocity pro fi les on the surface of the microcylinder.

微圆柱表面则采用(11)式所示的一阶滑移曲边界条件.

图5(a)给出了Re=20时,考虑稀薄效应(Kn=0.015)与不考虑稀薄效应(Kn=0)情况下微圆柱附近流线分布的对比.从图中可以看出,考虑稀薄效应时回流区长度明显缩短,这是由于气体-壁面滑移速度使得壁面附近流体微团动能增加,逆压梯度减小,从而分离涡变小.图5(b)给出了Kn=0.015,Re=20时,采用本文格式及half-way DBB格式模拟得到的微圆柱表面无量纲滑移速度分布同Beskok和Karniadakis[31]采用谱元方法计算得到结果的对比.由图可知,本文格式得到的模拟结果与谱元方法计算结果更为接近,在分离点之前几乎完全一致,在分离点之后存在一定偏差;而half-way DBB格式得到的模拟结果整体偏小,最大滑移速度较文献[31]的结果存在较大偏差.

3.4 同心微圆柱面Couette流

上述算例均为静止壁面上的滑移速度边界条件,为验证本文提出的格式亦能处理运动壁面上的滑移速度边界条件,本文模拟了同心微圆柱面旋转Couette流问题.如图6所示,内微圆柱的半径为R1(R1=30δx),以恒定的角速度ω逆时针旋转;外微圆柱的半径为R2,保持为静止状态;内外微圆柱的半径比R1:R2=3:5,其表面均为完全漫反射表面(σv1=σv2=1).

对于同心微圆柱面旋转Couette流,圆柱坐标系下的Navier-Stokes方程可简化为[23−26,30]

其中r为半径,uθ为切向速度.内外圆柱壁面处的气体速度边界条件为

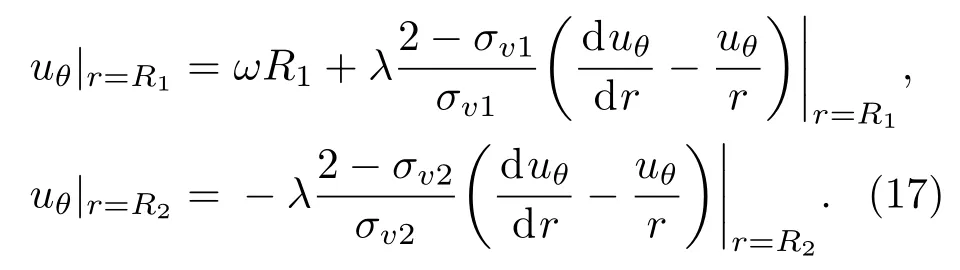
由此可得速度分布解析解为

其中系数A1,A2为

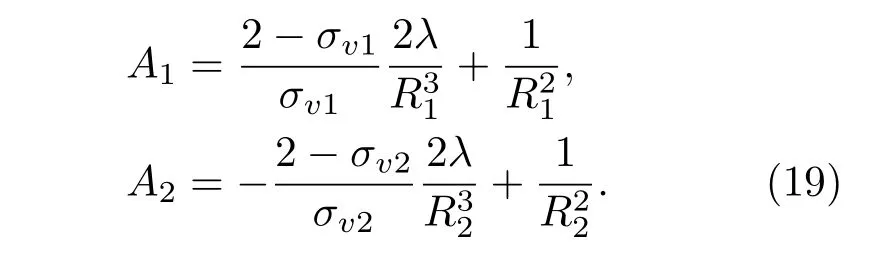
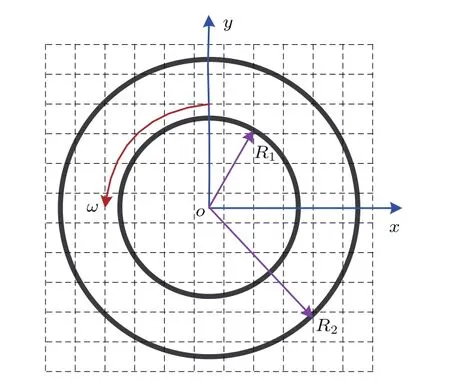
图6同心微圆柱面Couette流示意图Fig.6.Schematic illustration of the concentric microcylinder Couette fl ow.

图7 给出了Kn=0.05和Kn=0.1时,采用本文提出的格式、half-way DBB格式及Tao和Guo[24]提出的修正DBB格式计算得到的径向方向无量纲速度分布与解析解对比.由图7可知,本文格式的模拟结果始终与解析解符合良好;而halfway DBB格式和修正DBB格式模拟结果分别在内微圆柱附近和外微圆柱附近存在较大偏差;且Kn数越大,half-way DBB格式和修正DBB格式在边界处的偏差越明显.

表3给出了不同Kn数条件下,本文格式同half-way DBB格式和修正DBB格式计算结果误差对比情况.从表中可知,本文格式在模拟不同Kn数时最大相对误差及相对误差最小.且由表3可知,修正DBB格式在边界处最大相对误差较half-way DBB格式优势并不明显,但由于在其余区域符合较好,故在相对误差方面修正DBB格式比half-way DBB格式计算精度有所提高.

此外,为检验新格式的收敛性能,定义了流场的计算收敛判据:

其中,u(t+1)(i,j)为当前时刻流体格点的速度值,u(t)(i,j)为前一时刻流体格点的速度值.图8给出了Kn=0.05时,本文格式同half-way DBB格式和修正DBB格式收敛过程对比情况.由图8可知,三种边界处理格式的计算收敛时间相近.基于上述计算精度及收敛性能分析比较,本文提出的格式能更好地处理滑移区运动曲边界问题.

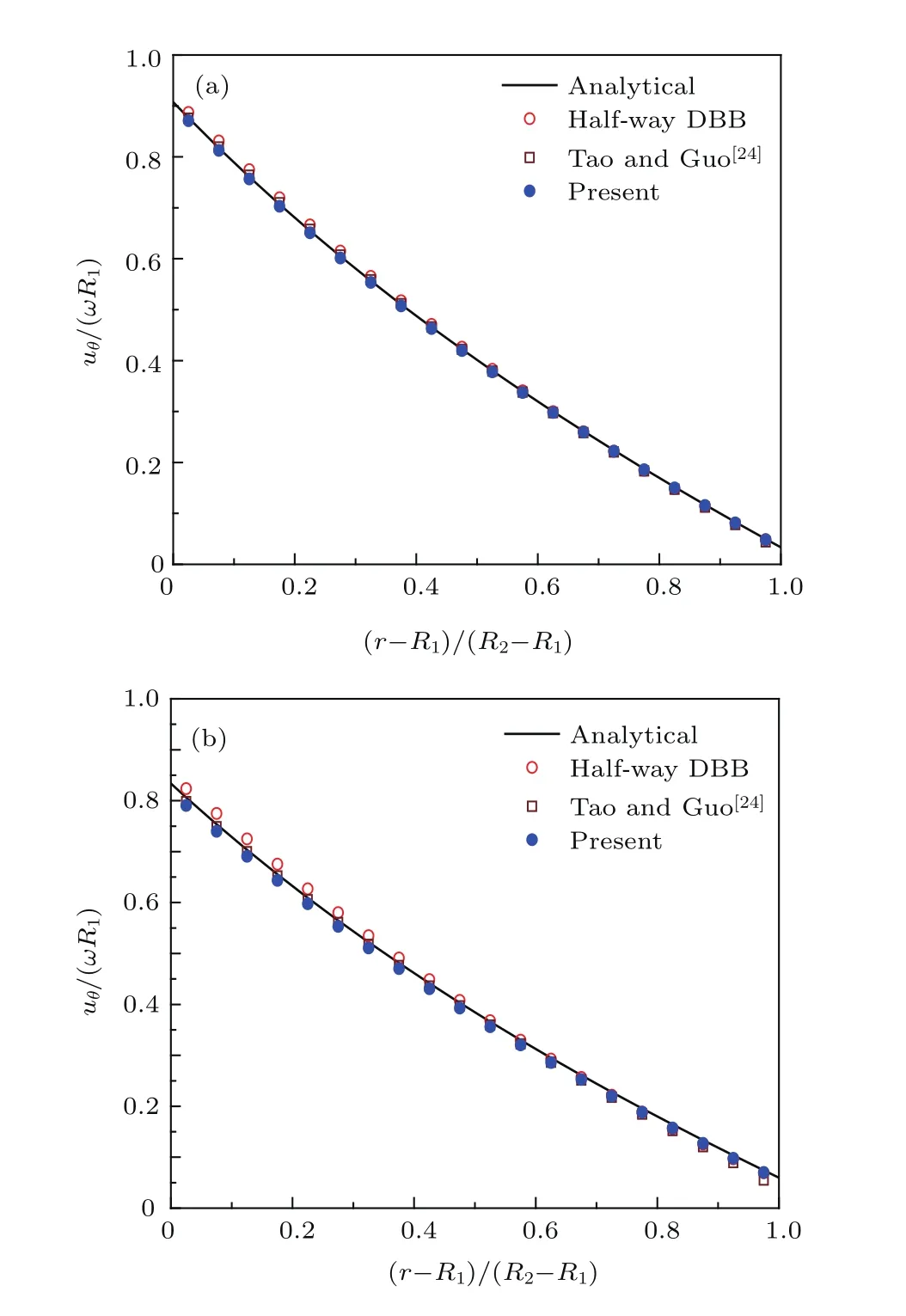
图7 (网刊彩色)微圆柱间Couette流无量纲速度分布(a)Kn=0.05;(b)Kn=0.1Fig.7.(color online)Normalized velocity pro fi les of the microcylinder Couette fl ow:(a)Kn=0.05;(b)Kn=0.1.

表3 不同Kn数条件下本文格式与half-way DBB格式及修正DBB格式计算误差对比Table 3.Computational errors of the present scheme,the half-way DBB scheme and the modi fi ed DBB scheme with di ff erent Kn numbers.

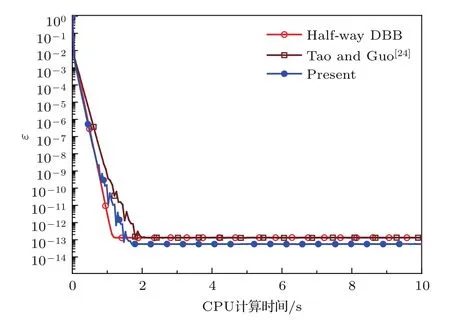
图8 (网刊彩色)不同格式的收敛曲线(Kn=0.05)Fig.8.(color online)Convergence pro fi les of di ff erent schemes(Kn=0.05).

4 结论

本文基于非平衡态外推格式处理曲边界与有限差分格式获取曲边界处宏观物理量及其法向梯度相结合的思想,提出了一种适用于滑移区复杂气-固边界的格子Boltzmann曲边界处理格式.该格式在处理复杂边界时考虑了实际物理边界与格线偏移量的影响,较half-way DBB格式具有更高的准确度;且该格式对气体-壁面相互作用参数选取无任何限定,相较修正DBB格式有更好的适应性.基于该格式对滑移区气体平直/倾斜微通道内Poiseuille流、微圆柱绕流和同心微圆柱面旋转Couette流问题进行计算分析,得到以下结论:

1)本文所提边界处理格式能够准确模拟网格线与实际物理边界不重合的平直以及倾斜微通道外力驱动Poiseuille流;而half-way DBB格式仅在特定偏移量条件下才能准确模拟平直微通道内Poiseuille流,且在模拟倾斜微通道内Poiseuille流时在壁面附近较理论值存在明显偏离;

2)通过对微圆柱气体绕流计算分析,发现考虑稀薄效应时回流区长度明显缩短;本文所提格式得到的微圆柱表面无量纲滑移速度与文献报道结果更为接近,而half-way DBB格式得到的结果整体偏小,且最大滑移速度存在较大偏差;

3)在模拟滑移区同心微圆柱面Couette流时,本文格式预测的径向方向无量纲速度分布与解析解符合良好,模拟精度较half-way DBB格式及修正DBB格式有明显提高.

综上可知,本文提出的曲边界处理格式具有处理滑移区复杂流固边界速度滑移问题的能力,且较half-way DBB格式和修正DBB格式分别有更高的精度和更好的适应性.此外,本文提出的曲边界处理格式,亦可推广处理微气体流动传热问题复杂流-固边界温度跳跃边界条件.

[1]Gad-el-Hak M 1999 ASME J.Fluids Eng.121 5

[2]Ho C M,Tai Y C 1998 Annu.Rev.Fluid Mech.30 579

[3]Zhang T T,Jia L,Wang Z C 2008 Chin.Phys.Lett.25 180

[4]Sun X M,He F,Ding Y T 2003 Chin.Phys.Lett.20 2199

[5]Liu C F,Ni Y S 2008 Chin.Phys.B 17 4554

[6]Tao S,Wang L,Guo Z L 2014 Acta Phys.Sin.63 214703(in Chinese)[陶实,王亮,郭照立2014物理学报63 214703]

[7]Wang Z,Liu Y,Zhang J Z 2016 Acta Phys.Sin.65 014703(in Chinese)[王佐,刘雁,张家忠2016物理学报65 014703]

[8]Guo Z L,Zheng C G,Shi B C 2002 Phys.Fluids 14 2007

[9]Mei R W,Luo L S,Shyy W 1999 J.Comput.Phys.155 307

[10]Ladd A J C 1994 J.Fluid Mech.271 285

[11]Noble D R,Torczynski J R 1998 Int.J.Mod.Phys.C 9 1189

[12]Yu Z,Yang H,Fan L S 2011 Chem.Eng.Sci.66 3441[13]Lee C H,Huang Z H,Chiew Y M 2015 Eng.Appl.Comp.Fluid 9 370

[14]Guo K K,Li L K,Xiao G,AuYeung N A,Mei R W 2015 Int.J.Heat Mass Tran.88 306

[15]Yin X W,Zhang J F 2012 J.Comput.Phys.231 4295

[16]Shi D Y,Wang Z K,Zhang A M 2014 Acta Phys.Sin.63 074703(in Chinese)[史冬岩,王志凯,张阿漫2014物理学报63 074703]

[17]Le G G,Oulaid O,Zhang J F 2015 Phys.Rev.E 91 033306

[18]Fu S C,Leung W W F,So R M C 2013 Commun.Comput.Phys.14 126

[19]Gao D Y,Chen Z Q,Chen L H,Zhang D L 2017 Int.J.Heat Mass Tran.105 673

[20]Izham M,Fukui T,Morinishi K 2011 J.Fluid Sci.Tech.6 812

[21]Nie D M,Lin J Z 2010 Chin.Phys.Lett.27 104701

[22]Fang H P,Wan R Z,Fan L W 2000 Chin.Phys.9 515

[23]Szalmas L 2007 Int.J.Mod.Phys.C 18 15

[24]Tao S,Guo Z L 2015 Phys.Rev.E 91 043305

[25]Guo Z L,Shi B C,Zheng C G 2011 Comput.Math.Appl.61 3519

[26]Suga K 2013 Fluid Dyn.Res.45 034501

[27]Yang W L,Li H X,Zhang T J,Elfadel I M 2015 ASME 2015 13th International Conference on Nanochannels,Microchannels,and Minichannels San Francisco,CA,USA,July 6–9,2015 pV001T04A001

[28]Buick J M,Greated C A 2000 Phys.Rev.E 61 5307

[29]Guo Z L,Zheng C G,Shi B C 2002 Phys.Rev.E 65 046308

[30]Sun Y H,Barber R W,Emerson D R 2005 Phys.Fluids 17 047102

[31]Beskok A,Karniadakis G E 1994 J.Thermophys.Heat Tr.8 647

PACS:47.11.Qr,47.15.Rq,02.60.CbDOI:10.7498/aps.66.114701

A new curved boundary treatment in lattice Boltzmann method for micro gas fl ow in the slip regime∗

Gu JuanHuang Rong-ZongLiu Zhen-YuWu Hui-Ying†
(School of Mechanical Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

18 December 2016;revised manuscript

5 April 2017)

A new curved boundary treatment in lattice Boltzmann method is developed for micro gas fl ow in the slip regime.The proposed treatment is a combination of the nonequilibrium extrapolation scheme for curved boundary with noslip velocity condition and the counter-extrapolation method for the velocity and its normal gradient on the curved boundary.Taking into consideration the e ff ect of the o ff set between the physical boundary and the closest grid line,the new treatment is proved to be more accurate than the traditional half-way di ff usive bounce-back(DBB)scheme.The present treatment is also more applicable than the modi fi ed DBB scheme because the speci fi c gas-wall interaction parameters need to be determined to ensure the validation of the modi fi ed DBB scheme.

The proposed boundary treatment is implemented to simulate the benchmark problems,which include a Poiseuille fl ow in the aligned/inclined micro-channel,a fl ow past a microcylinder and a microcylindrical Couette fl ow.The results and conclusions are summarized as follows.

1)The force-driven Poiseuille fl ow in an aligned microchannel is simulated separately with di ff erent values of wallgrid o ff set qδx(q=0.25,0.5,0.75,1.0).With the consideration of the wall-grid o ff set,the numerical results with the new boundary treatment show good agreement with the analytical solutions.However,the results obtained by using the half-way DBB scheme only accord well with the analytical solutions under the condition of a fi xed wall-grid o ff set(q=0.5).

2)To demonstrate the capability of the present treatment in dealing with gas fl ow in a more complex geometry,the force-driven Poiseuille fl ow in a micro-channel is investigated separately with di ff erent inclined angles.The present numerical results fi t well with the analytical solutions.However,the discrepancy between the results obtained with the half-way DBB scheme and the analytical solutions can be clearly observed near the inclined boundaries.

3)The gas fl ow past a microcylinder is simulated to prove that the present treatment can deal with the curved boundary.The slip velocity pro fi le along the micro cylinder periphery obtained with the present treatment accords well with the available data in the published literature.However,the results obtained with the half-way DBB scheme show lower values than the results from the published work.

4)In the simulations of the microcylindrical Couette fl ow between two coaxial rotating cylinders for di ff erent Knudsen numbers the results obtained by using the present treatment show excellent agreement with the analytical solutions.However,the results obtained with the half-way DBB scheme and the modi fi ed DBB scheme deviate obviously from the analytical solutions near the inner and outer cylindrical walls,respectively.

In summary,the new boundary treatment proposed in this work is capable of dealing with the complex gas-solid boundary in the slip regime.The new treatment has a higher accuracy than the half-way DBB scheme and shows a better applicability than the modi fi ed DBB scheme.

curved boundary,lattice Boltzmann method,slip regime,micro gas fl ow

10.7498/aps.66.114701

∗国家自然科学基金(批准号:51536005,51521004)资助的课题.

†通信作者.E-mail:whysrj@sjtu.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.51536005,51521004).

†Corresponding author.E-mail:whysrj@sjtu.edu.cn